3次関数の最大・最小の応用問題｜文章題（図形）の解き方3ステップ【数II微分】

本記事では、3次関数を用いた図形問題の解き方をステップ形式で徹底解説します。

図形が絡む応用問題では、単に微分して増減表を書くだけでなく、「どの値を変数 $\small x$ と置くか」、「図形の条件から$\small x$の範囲をどう定義するか」を問題文から判断することがポイントになります。

立体（円錐・球体など）の体積など、試験に出やすい頻出パターンを例題に、解き方のポイントを確認していきましょう！

3次関数の最大・最小の応用
1. 【問題1】箱の容積の最大化
2. 【問題2】円錐の体積の最大

3次関数の最大・最小の応用

【問題1】箱の容積の最大化

1辺の長さが18cmの正方形の厚紙がある。厚紙の4隅から1辺の長さが同じ大きさの正方形を切り取り、その残りを折り曲げてふたのない箱を作る。この箱の容積を最大にするには、切り取る正方形の長さをいくらにすればよいか求めよ。

問題解決のKey

図形が絡む最大・最小の問題は次の3ステップで解くのが定石です。
STEP１：求めたいものを文字 $\small x$でおく。
　　　　このときに、文字の取り得る値の範囲も確認する。
STEP２：最大・最小化したいものを$\small x$で表す。
STEP３：微分して最大・最小を求める問題に帰着させる。

　解説

4隅から切り取る正方形の1辺の長さを$\small x$cmとおきます。$\small x$は1辺が18cmの厚紙から切り取る正方形の1辺の長さなので、

$$\small 0<x<9 \space \cdots ①$$

を満たしている必要があります。

補足：$\small x$が取り得る値の範囲

$\small x$は長さなので0より大きい値になるのは分かりやすいと思いますが、上限値は「$\small x<18$でもよいのではないか？」と考えた人もいるでしょう。確かに、1辺が18cmの厚紙なので18cm未満と設定したくなりますが、今回は4隅から切り取る必要があるので、切り取る正方形の1辺は厚紙の1辺の半分よりも短くなっている必要があります。
例えば仮に15cmずつ4隅から切り取ろうとした場合、厚紙の左右から15cmずつ切り取ることになるので、合計で30cm分を切り取ることになりますが、これは厚紙の1辺の長さである18cmを超えてしまいます。このことを考慮すると、切り取る正方形の1辺あたりの長さ上限は半分未満の9cm未満である必要が出てきます。
このことをもう少し数学的に機械的に導き出したければ、『厚紙の1辺である18cmが左右から切り取られる正方形の合計の長さである $\small x+x=2x$よりも長くなる必要がある』という不等式を満たすことになります。

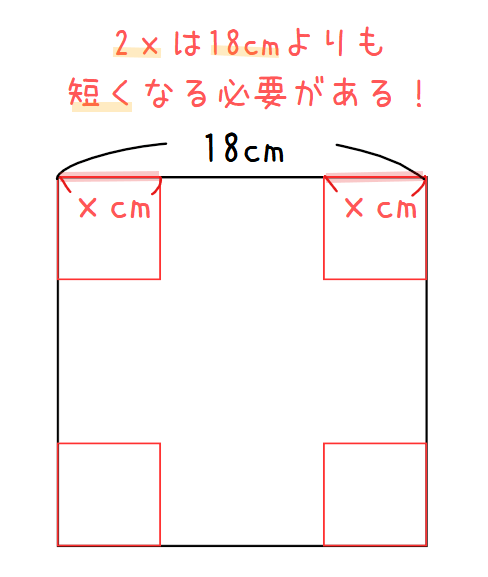
よって、
\begin{split}
&\small x+x < 18 \\
&\small 2x < 18 \\
&\small x < 9 \\
\end{split}
と求められます。

容積を求めるために必要な情報は底面の面積と高さになるので、下図のように各種辺の長さを$\small x$を用いて求めていくことで

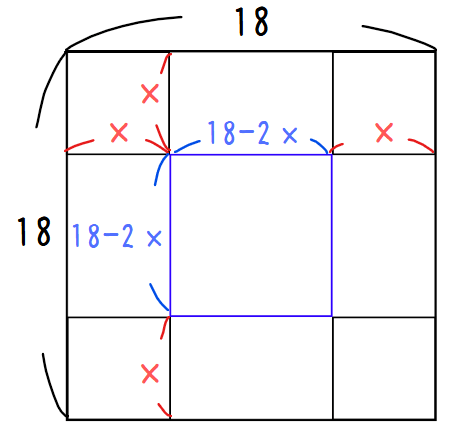
\begin{cases}
\small （底面積）=(18-2x)^2\\
\small （高さ）=x\\
\end{cases}

であることから、箱の容積を$\small y \space \mathrm{cm}^2$とすると

\begin{split}
\small y=x(18-2x)^2
\end{split}

と表すことができます。

今回求めたいのは容積$\small y$が最大になるような$\small x$の値なので、$\small x(18-2x)^2$を微分して①の範囲での最大値を求めればOKです。

Point

ここまでの内容をまとめると、今回の問題は
$\small 0< x <9$において、$\small y=x(18-2x)^2$が最大となるような$\small x$の値を求めよ。という問題に帰着します。

$\small x(18-2x)^2$の微分は、このままだと微分公式 $\small (x^n)^\prime = nx^{n-1}$が使えないので展開してあげると

\begin{split}
\small x(18-2x)^2 &\small =x(324-72x+4x^2)\\
& \small =4x^3-72x^2+324x\\
\end{split}

となるので、

\begin{split}
\small y^\prime =12x^2-144x+324\\
\end{split}

極値では微分係数の傾きが0になる、すなわち$\small y^\prime =0$となるので

\begin{split}
&\small y^\prime =0\\
\small \Leftrightarrow \space &\small 12x^2-144x+324=0\\
\small \Leftrightarrow \space &\small x^2-12x+27=0 \space \color{#ef5350}{◀12で約分}\\
\small \Leftrightarrow \space &\small (x-3)(x-9)=0\\
\small ∴ \space &\small x=3, \space 9\\
\end{split}

よって、$\small y=x(18-2x)^2$は$\small 0<x<9$の範囲では$\small x=3$で極値をとることが分かったので、増減表は以下のようになります。

補足：3次関数のグラフの概形

3次関数の極値は、$\small x^3$の係数が正であれば左から順に『極大、極小』となり、$\small x^3$の係数が負であれば『極小→極大』となることを知っていれば、$\small y^\prime$の符号を調べる手間を減らせます。

本問であれば、$\small x=3$で極大、$\small x=9$で極小になります。

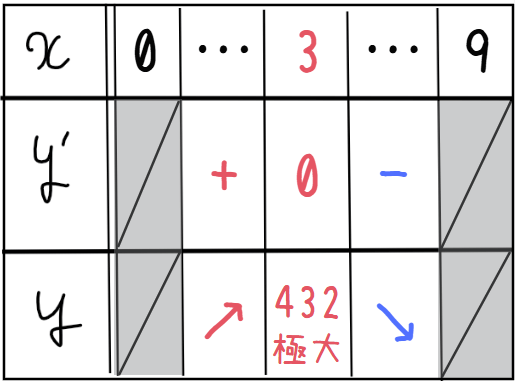
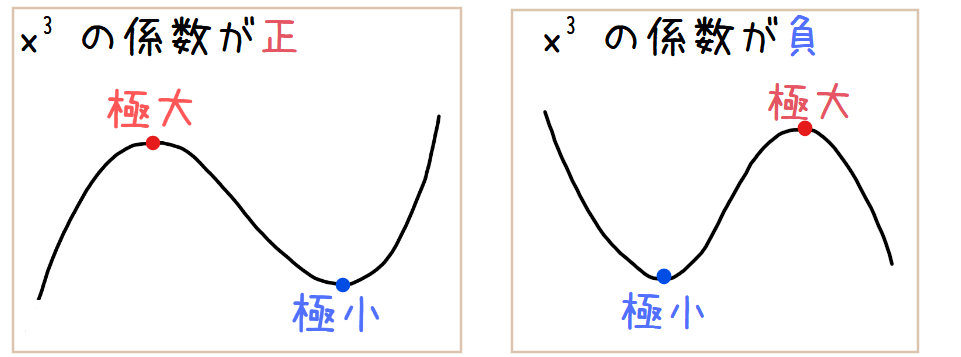
よって、$\small y$は$\small x=3$のとき最大値 $\small 432$をとることから、容積 $\small y$が最大になるときの切り取る正方形の1辺の長さ $\small x$は、$\small 3 \mathrm{cm}$…【答】.

【問題2】円錐の体積の最大

底面の半径と高さの和が30cmである円錐を考える。円錐の体積が最大となるときの底面の半径と高さを求めよ。

問題解決のKey

文字設定は、微分計算が楽になるように設定せよ！

　解説

円錐の半径を$\small x$とおくと、半径と高さの合計が30cmなので、高さは$\small 30-x$と表せます。

補足：半径と高さのどちらを文字でおく？

半径と高さのどちらを文字でおいても答え自体は求められますが、円錐の体積を求める公式が（円錐の体積）=$\small \displaystyle \frac{1}{3}\pi$×（半径）$\small ^2$×（高さ）
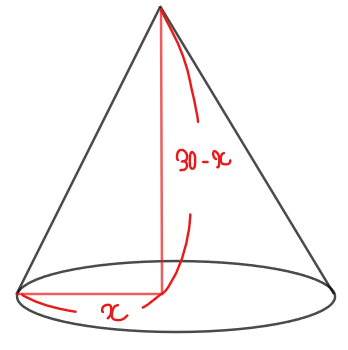
であることを考えると、仮に高さを$\small x$とおいた場合、半径が$\small 30-x$となり微分するために$\small (30-x)^2$の展開が必要になるので計算がめんどくさくなります…。
そのため、今回は半径を$\small x$とおいた方が計算が楽になります。

ただし、$\small x$と$\small 30-x$は長さなので0より大きな値となる必要があることから、

\begin{split}
&\small x>0 \space かつ \space 30-x>0\\
\small \Leftrightarrow \space &\small x>0 \space かつ \space x<30\\
\small ∴ \space &\small 0<x<30 \space \cdots ①\\
\end{split}

円錐の体積を$\small y$とおくと、

\begin{split}
\small y &\small=\frac{1}{3}\pi x^2(30-x)\\
&\small=\frac{1}{3}\pi (30x^2-x^3)\\
\end{split}

$\small y$の極値は

\begin{split}
&\small y^\prime = 0\\
\small \Leftrightarrow \space &\small \frac{1}{3}\pi (60x-3x^2)=0\\
\small \Leftrightarrow \space &\small x(20-x)=0\\
\small ∴ \space &\small x=0, \space 20\\
\end{split}

このうち$\small x$の取り得る値の範囲である①を満たすのは$\small x=20$のため、円錐の体積 $\small y$は底面の半径 $\small x$が20cmのときに極値をとることが分かります。

このときが極大になることは増減表をかくことで確認できます。

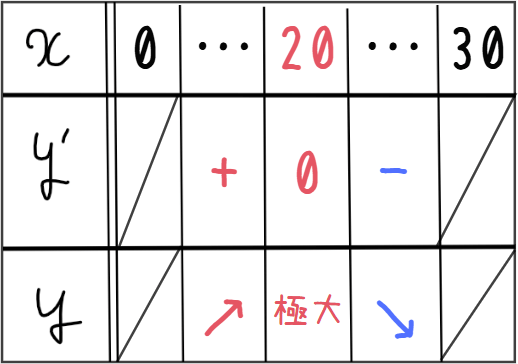
問題1の補足で解説した3次関数のグラフの概形から考えても、今回の3次関数は$\small x^3$の係数が負なので、$\small x=0$で極小、$\small x=20$で極大になることが分かります。

このときの高さは$\small 30-20=10 \mathrm{cm}$です。

よって、円錐の体積が最大となるときの半径は$\small 20 \mathrm{cm}$、高さは$\small 10 \mathrm{cm}$…【答】となります。

補足：和が一定であるときの最大値

本問のように和が一定という条件のもとで、ある量（今回であれば体積）を最大にする場合、最大となるときの変数の値は、指数の比で分配されるという法則があります。
本問であれば、体積を最大にするときの$\small r$（半径）と$\small h$（高さ）は、体積は$\small \displaystyle \frac{1}{3}\pi r^2 h$の公式からもわかるように$\small r^2$、$\small h^1$に比例するので、体積が最大になるときの$\small r,h$の値は $\small r:h =2:1$（指数の比）となるように30cmが分配されるので、
\begin{split}
&\small r=\frac{2}{1+2}\times 30 = 20 \mathrm{cm}\\
&\small h=\frac{1}{1+2}\times 30 = 10 \mathrm{cm}\\
\end{split}
のように簡単に求めることができます。検算にも使えて便利なので余裕があれば覚えておくと役立ちます。

今回は以上です。お疲れさまでした！