【徹底解説】三角方程式の解き方（三角関数の合成、2次関数の利用、角度の範囲から解く）

「三角方程式の解き方が分からない…」という悩みを抱えている人向けに、三角方程式の解き方について解説していきます。三角方程式には大きく3つの種類があります。角度の範囲から解く問題、三角関数の合成を利用する問題、2次関数に置き換えて解く問題です。

本記事では、「1.目標」の問題を解けるようになることを目標とします。苦手だなと思う人は、詳しく説明しているので、ぜひ最後まで読んでみてください！また、ここでは三角関数の実践編として、様々な種類の方程式の解き方を解説しているので、そもそも三角方程式の基本的な解き方を知りたいという方は、三角方程式の解法をご覧ください。

　本記事のレベル

重要度

低

1

2

3

4

5

高
難易度

易しい

1

2

3

4

5

難しい
暗記/理解

暗記重視

1

2

3

4

5

理解重視

目標
【問題＆解説】三角方程式の解き方
本記事のまとめ

目標

目標とする問題は以下の通りです。

問題

$\small 0 ≦ \theta < \pi$のとき、以下を満たす$\small \theta $を求めよ。
$\small (1) \sin 2\theta = \frac{\sqrt{3}}{2}$
$\small (2) \sin (\theta-\frac{\pi}{3}) = -\frac{1}{2}$

$\small 0 ≦ \theta < 2\pi$のとき、以下を満たす$\small \theta $を求めよ。
$\small (3) \sin \theta + \cos\theta = 1$
$\small (4) 2\cos^2 \theta + 5\sin\theta -4 = 0$

ざっくりいうと、(1)(2)は、三角関数の角度の範囲から解く問題（角度が変化しているバージョン。難しく言うと位相ずれ、範囲制限パターン）、(3)は、合成関数を利用する問題、(4)は、2次関数に置き換えて解く問題です。どれも、三角関数ではよく出る形式なので、ここでマスターしておきましょう。

「3.チャレンジ問題」では、「1.目標」の問題を理解できていれば、解ける問題を応用編として記載しているので、最後に復習として解いてみるとよいと思います。

【問題＆解説】三角方程式の解き方

【問題1】角度の範囲から解く（角度倍数パターン）

問題1：角度の範囲から解く（角度倍数パターン）

$\small 0 ≦ \theta < \pi$のとき、以下を満たす$\small \theta $を求めよ。
（1）$\small \displaystyle \sin 2\theta = \frac{\sqrt{3}}{2}$

解答（1）

sinの中身の角度を見ると$\small \theta$ではなく$\small 2\theta$になっていることに注意しましょう。角度が2倍されていたり、足し引きされているような場合は、それに伴って考えるべき角度の範囲も変わるのでまずは忘れないうちに範囲を求めておきましょう。今回の範囲は、$\small 0 ≦ \theta < \pi$と書かれているので全体を2倍して、$\small 0 ≦ 2\theta < 2\pi$です。単位円上を1周する範囲で考えればいいということですね。範囲を確認したら、ここからは三角方程式を解いてきます。相も変わらず、単位円を描いて求めていきましょう。

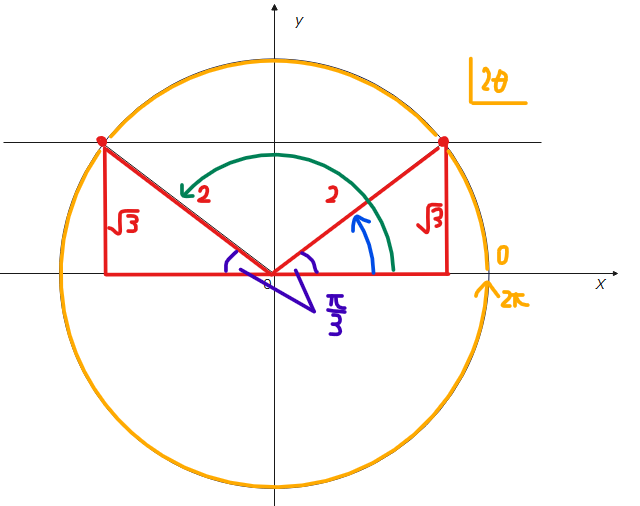
上の図の書き方が分からないという方は、「三角方程式の解き方」で解説しているので確認してみましょう。上の図の右上に$\small 2\theta$と書いています。これは、この図に書いた角度はあくまで$\small 2\theta$ですよ、というのを忘れないため書いてます。よって、青色の角度は$\small 2\theta=\frac{\pi}{3}$、緑色の角度は、$\small 2\theta=\frac{2}{3}\pi$です。あとは、今求めた角度は$\small 2\theta$なので、2で割ってあげれば、答えになります。

（解答）
$\small \quad \displaystyle \theta=\frac{\pi}{3}、\frac{\pi}{6} $

【問題2】角度の範囲から解く（位相ずれパターン）

問題2：角度の範囲から解く（位相ずれパターン）

$\small 0 ≦ \theta < \pi$のとき、以下を満たす$\small \theta $を求めよ。
（2）$\small \displaystyle \sin \left(\theta-\frac{\pi}{3} \right) = -\frac{1}{2}$

解答（2）

sinの中身の角度が、$\small \theta-\frac{\pi}{3}$なので、今回の角度の範囲はどうなるでしょう？
$$\small 0 ≦ \theta < \pi$$ $$\small -\frac{\pi}{3}≦ \theta-\frac{\pi}{3} < \pi-\frac{\pi}{3}$$ $$\small -\frac{\pi}{3} ≦ \theta-\frac{\pi}{3} < \frac{2}{3}\pi$$ こんな感じですが、正直、角度が$\small -\frac{\pi}{3}$から$\small \frac{2}{3}\pi$と言われてもイメージできないですよね。私もよくわかりません。なので、足し引きされているときは上記計算式の2段目の式（引き算の計算をする前の式）で考えるのが個人的にはおすすめです。このようにしておくと、図を描くときに範囲が分かりやすいです。今回の図は以下のようになります。

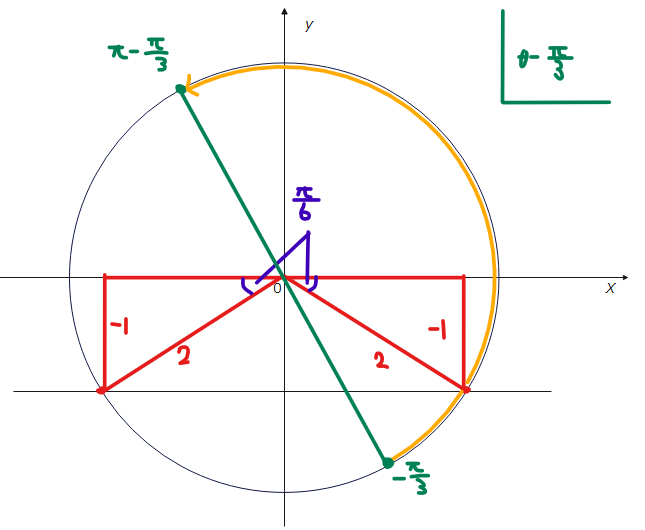
$\small \frac{\pi}{3}$は60°、$\small \frac{\pi}{6}$は30°という大小関係にだけ注意して図を描きます。緑の線が$\small -\frac{\pi}{3}$と$\small \pi-\frac{\pi}{3}$を表していて、オレンジが今回考える範囲です。先程2番目の式で計算を止めておいたのは、この線を描くときに$\small \pi-\frac{\pi}{3}$としておくと、180°から60°戻った位置とイメージしやすいかなと思ったからです（図が書ければよいので、この辺りは皆さんのやりやすいようにカスタマイズしてください…）。
範囲を見ると右下の解は範囲内ですが、左下の解は範囲外ですね。右下の解の角度は、0°から時計回りに$\small \frac{\pi}{6}$進んだ角度なので、$\small -\frac{\pi}{6}$となることに注意しましょう（$\small \frac{11}{6}\pi$ではない）。よって今回の解は、
$\small \theta- \frac{\pi}{3}=-\frac{\pi}{6}$
$\small \theta =-\frac{\pi}{6}+\frac{\pi}{3}$
∴ $\small \theta =\frac{\pi}{6}\space\cdots(答)$

（解答）
$\small \quad \displaystyle \theta =\frac{\pi}{6} $

【問題3】三角関数の合成を利用して解く

問題3：三角関数の合成を利用して解く

$\small 0 ≦ \theta < 2\pi$のとき、以下を満たす$\small \theta $を求めよ。
（3）$\small \sin \theta + \cos\theta = 1$

■三角関数の合成を使うときの判断ポイント
　sinとcosが混ざってる1次式かつ互いに同一位相なら三角関数の合成を利用する！

sinとcosが混ざった2次式の場合は、問題4で紹介する「2次関数に置き換えて解く」解法を使います。

（補足）同一位相ってなに？
sinやcosの角度部分のことを位相といいます。同一位相とは角度部分の形が一緒ということです。
【同一位相の例】
　・$\small \sin\color{red}{2\theta}$と$\small \cos\color{red}{2\theta}$
　・$\small \displaystyle \sin\color{red}{\left(3\theta+\frac{\pi}{4}\right)}$と$\small \displaystyle \cos\color{red}{\left(3\theta+\frac{\pi}{4}\right)}$

解答（3）

続いては、今までとは様子が違いますね。sinもcosも入っています。このままだと解けないので、(1)や(2)のような、sinだけ、cosだけの形に持っていけないでしょうか。このような場合は、三角関数の合成公式が使えます。合成公式についてよくわからないという方は、以下に解説しているので確認してみてください。

★三角関数の合成公式
$\small a\sin\theta + b\cos\theta = \sqrt{a^2+b^2}\sin(\theta + \alpha)$
ただし、$\small \sin\alpha=\frac{b}{\sqrt{a^2+b^2}}、\cos\alpha=\frac{a}{\sqrt{a^2+b^2}}$.
こんな式でした。式で書くとごついですが、個人的には合成公式は公式そのものを覚えるよりもに使い方で覚えた方がいい公式なので、使い方が怪しい人はここで習得しましょう。
まず、以下のような図を描きます。

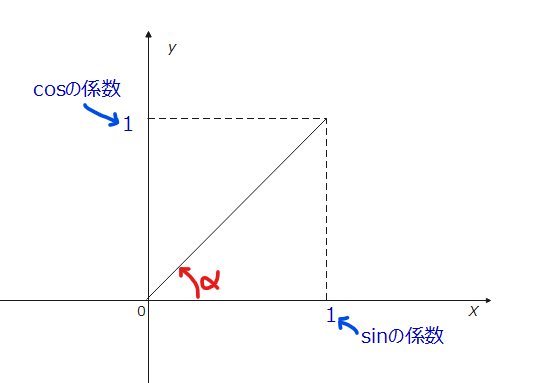
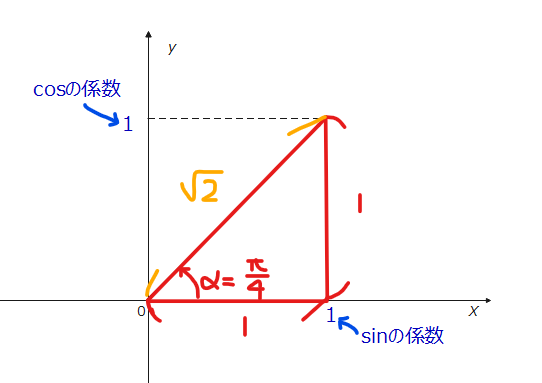
x座標には、sinの係数、y座標にはcosの係数をとって、座標と原点を線で結びます。今回はどちらも1なので点(1,1)と原点を結びます。この図を描くと、実は、線分の長さが合成公式の$\small \sqrt{a^2+b^2}$、結んだ線とx軸の角度が$\small \alpha$となります。なのでそれぞれ求めると線分の長さは$\small \sqrt{2}$、$\small \alpha = \frac{\pi}{4}$となります（下図）。

よって、
$$\small \sin\theta + \cos\theta = \sqrt{2}\sin(\theta + \frac{\pi}{4})$$ と変形できます。

合成公式を使うことで、
$$\small \sin \theta + \cos\theta = 1$$ $$\small \sqrt{2}\sin(\theta + \frac{\pi}{4}) = 1$$ $$\small \sin(\theta + \frac{\pi}{4}) = \frac{1}{\sqrt{2}}$$ ここまで式変形すると、(2)と同じ形式なので解けそうですね。図を描いて解いてみましょう。今回は角度の範囲が$\small 0 ≦ \theta < 2\pi$なので今考えるべき角度の範囲は、
$$\small \color{blue}{\frac{\pi}{4}} ≦ \theta+\color{blue}{\frac{\pi}{4}} < 2\pi + \color{blue}{\frac{\pi}{4}}$$ であることに注意します。下図で言うと、黄色で示している緑ラインから始まる一周が範囲。ただし$\small \frac{\pi}{4}$は含むが、$\small 2\pi + \frac{\pi}{4}$は含まない。

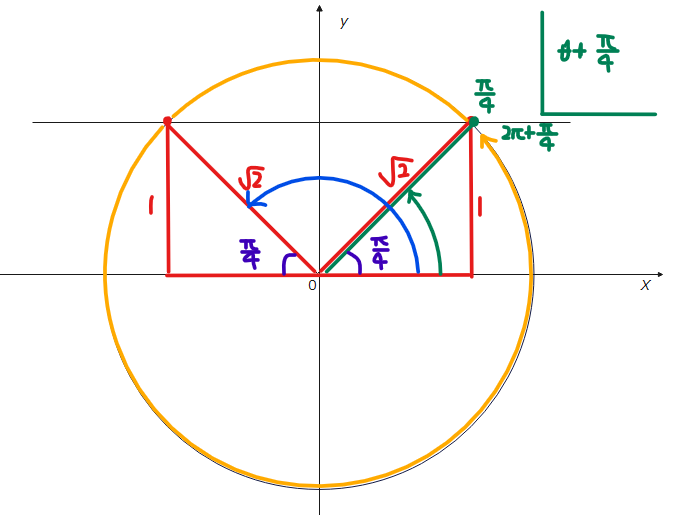
なので、緑の角度と青の角度が範囲内では解となるので、$\small \theta =\frac{\pi}{4}、\frac{3}{4}\pi $…としたくなりますが、
$$\small \theta + \frac{\pi}{4} = \frac{\pi}{4}、\frac{3}{4}\pi$$ ですね。このようなミスを防ぐためにも、図の右上のように今求めている角度を明記しておくといいと思います。
よって、求める角度は、 $\small \theta =0、\frac{\pi}{2} \space\cdots(答)$

（解答）
$\small \displaystyle \quad \theta =0、\frac{\pi}{2}$

【問題4】2次関数に置き換えて解く

問題4：2次関数に置き換えて解く

$\small 0 ≦ \theta < 2\pi$のとき、以下を満たす$\small \theta $を求めよ。
（4）$\small 2\cos^2 \theta + 5\sin\theta -4 = 0$

解答（4）

2次方程式のような形をしています。この場合は、そのまま2次方程式として解いていくのがよいです。ただ、今は、sinとcosの両方が式の中に入っているので、どちらか一方だけになるように統一します。統一の仕方は難しくなく、$\small \sin^2\theta + \cos^2\theta = 1$を使えばOK。
$$\small \sin^2\theta + \cos^2\theta = 1$$ $$\small \cos^2\theta = 1-\sin^2\theta$$ より、問題の式に代入すると、
$$\small 2\cos^2 \theta + 5\sin\theta -4 = 0$$ $$\small 2(1-\sin^2\theta) + 5\sin\theta -4 = 0$$ $$\small 2-2\sin^2\theta + 5\sin\theta -4 = 0$$ $$\small -2\sin^2\theta + 5\sin\theta -2 = 0$$ $$\small 2\sin^2\theta -5\sin\theta +2 = 0$$ ここまでくれば、2次方程式として解けますね。まだ慣れない人は、$\small\sin\theta$を$\small x$とおいてあげるとわかりやすいです。 $$\small 2x^2 -5x +2 = 0$$ $$\small (2x-1)(x-2) = 0$$ $$\small x=\frac{1}{2}、2$$ あとは、$\small x$を$\small\sin\theta$に置き換えてあげると、 $$\small \sin\theta=\frac{1}{2}、\sin\theta=2$$ この形まで来ると、あとは三角比の問題なので、$\small 0 ≦ \theta < 2\pi$の範囲で$\small \theta$の値を求めていきましょう。
まず、$\small \sin\theta = \frac{1}{2}$から解いてみます。図は以下の通りなので

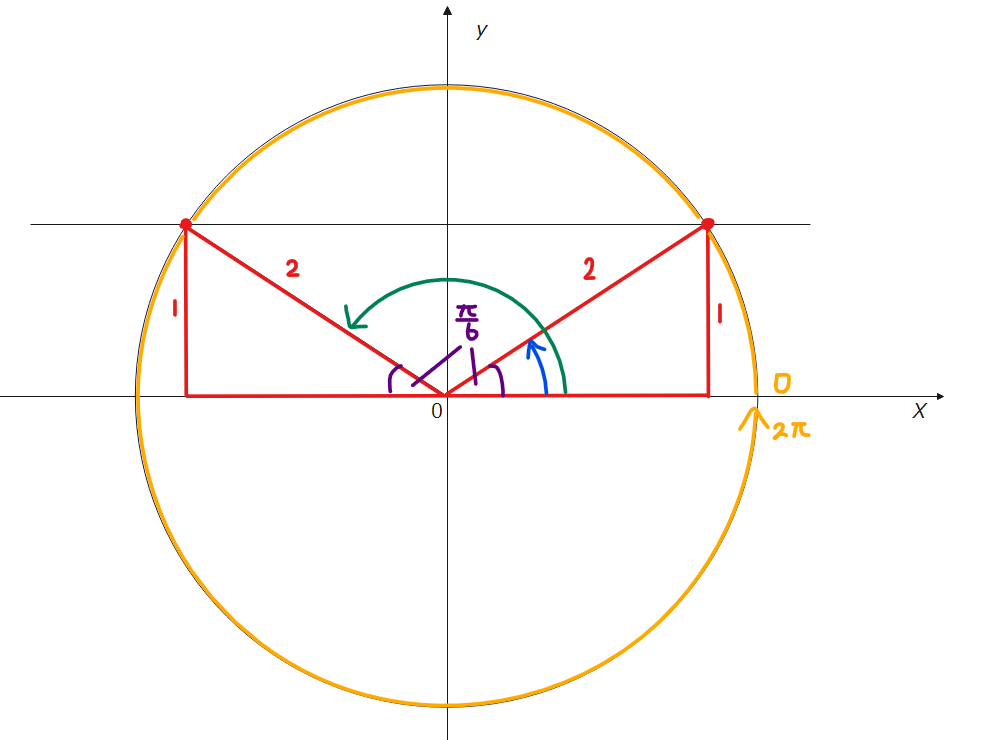
$$\small \color{red}{\theta = \frac{\pi}{6}、\frac{5}{6}\pi}$$ もう一方の$\small \sin\theta=2 $については、sinはそもそも-1～1の値しかとらないので、$\small \sin\theta=2 $となるような角度$\small \theta$はないです。よって、解なし。
以上から、答えは、
$\small \theta = \frac{\pi}{6}、\frac{5}{6}\pi \space \cdots$(答)

（解答）
$\small \displaystyle \quad \theta = \frac{\pi}{6}、\frac{5}{6}\pi $

チャレンジ問題

これまでの問題の知識、考え方を使えば解ける問題になっているので、ぜひチャレンジしてみましょう。また、つまずいた場合は、その箇所がまだ理解が浅い箇所になるので、問題1～4の解き方を再度復習してみましょう。

チャレンジ問題

$\small 0 ≦ \theta < 2\pi$のとき、$\small\cos2\theta-\sqrt{3}\sin2\theta-1=0$を解け。

解答

sinとcosが混ざっている1次式かつ同一位相なので三角関数の合成を行うと、 $$\small\cos2\theta-\sqrt{3}\sin2\theta-1=0$$ $$\small\sqrt{3}\sin2\theta-\cos2\theta=-1$$ $$\small 2\sin\left(2\theta-\frac{\pi}{6}\right)=-1$$ $$\small \sin\left(2\theta-\frac{\pi}{6}\right)=-\frac{1}{2}$$

角度の範囲は、
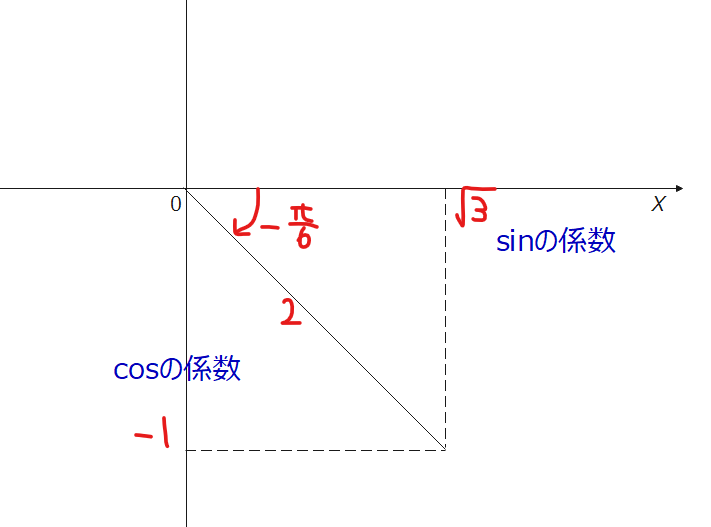
$$\small 0 ≦ \theta < 2\pi$$ $$\small 0 ≦ 2\theta < 4\pi$$ $$\small \color{blue}{-\frac{\pi}{6}} ≦ 2\theta – \color{blue}{\frac{\pi}{6}} < 4\pi\ – \color{blue}{\frac{\pi}{6}}$$

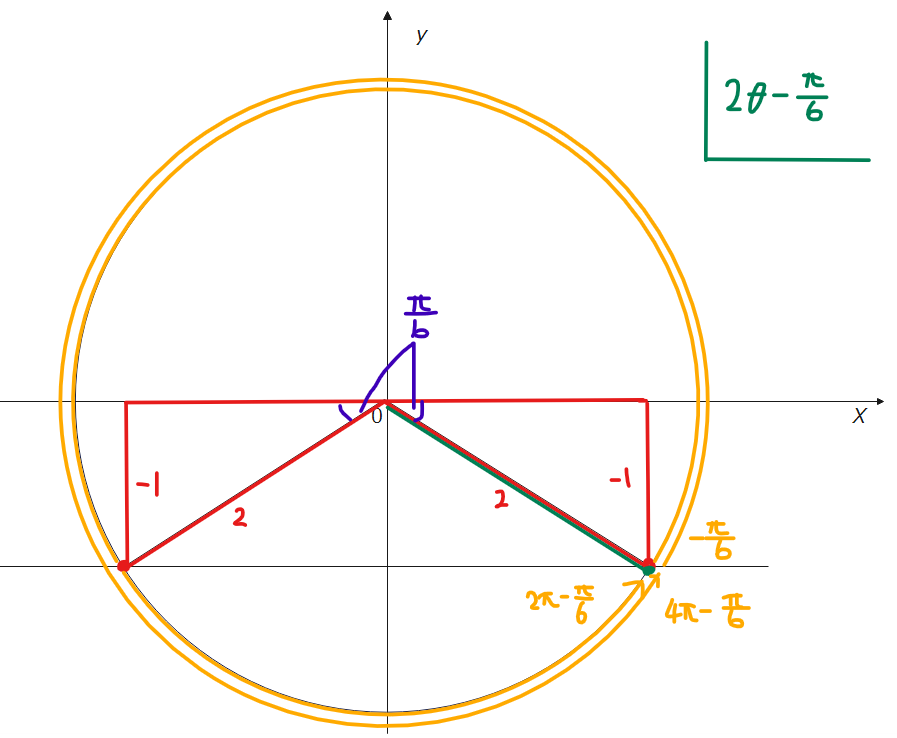
範囲は、$\small 4\pi\ – \frac{\pi}{6}$までなので、2周分あることに注意して、該当する角度は、 $$2\theta – \frac{\pi}{6} = -\frac{\pi}{6}、\pi+\frac{\pi}{6}、2\pi-\frac{\pi}{6}、3\pi+\frac{\pi}{6}$$ $\small 4\pi\ – \frac{\pi}{6} $は範囲外（不等号のイコールなし）なので注意。 $$2\theta = 0、\pi+\frac{2\pi}{6}、2\pi、3\pi+\frac{2\pi}{6}$$ $$2\theta = 0、\frac{4\pi}{3}、2\pi、\frac{10\pi}{3}$$ $$\theta = 0、\frac{2}{3}\pi、\pi、\frac{5}{3}\pi\space\cdots(答)$$

（解答）
$\small \displaystyle \quad \theta = 0、\frac{2}{3}\pi、\pi、\frac{5}{3}\pi $