今回は、三角関数の最大値、最小値を求める問題についてパターンごとにわかりやすく解説します。三角関数の最大値、最小値の求め方は問題によって、ある程度パターン化されていて、2次関数に落とし込む方法や三角関数の合成をして解く方法などがあります。本記事では、重要度の高い5パターンについて各パターンの見分け方や解き方のコツを解説するので、ぜひ最後まで読んでみてください!
- 三角関数の最大最小を求める方針がたくさんありすぎて分からない…
- sin、cosを文字で置き換えて最大最小を求めるのが苦手…
- θの範囲を求めるのが苦手…
- 三角関数の最大値、最小値を求めるコツを知りたい!
三角関数の問題パターンと解き方のコツ
三角関数の最大最小は問題によって解き方が異なるので、どの解き方で解けばいいのか悩む人も多いと思います。今回は、そんな人向けに絶対に覚えておきたいパターンを5つ紹介します。この5パターンを覚えておけばだいたいの問題は解くことができるので、ぜひ考え方を理解してください。
本記事では触れませんが、ここで紹介する5パターン以外にも数Ⅲで習う三角関数の微分法を使って最大値、最小値を求める方法もあります。ただ、微分での計算は煩雑なことも多いので、今回は三角関数について微分を使わずに解くための方法に絞って解説していきます!
三角関数の最大最小-問題パターン5選
結論、三角関数の最大値、最小値の問題は以下の5パターンで解くことができます。
■三角関数の最大値、最小値の解法パターン5選
- 2次関数に落とし込んで解く
- 三角関数の合成で解く
- 2倍角の公式で次数下げして解く
- \(\small t= \sin\theta+ \cos\theta\)とおいて解く
- 図形的に解く
パターン①:2次関数に落とし込んで解く
この解法が一番基本的な解き方になります。sinやcosをtとおいてtの2次関数の最大値、最小値を求める方法です。θの範囲によってsinやcosの取り得る範囲が変わるため、sinやcosをtとおいた際にtの範囲を計算しておき、tの範囲内で最大最小を考えることがポイントです。
また、そのときの\(\small \theta\)の値も求めよ。
■三角関数の最大値・最小値の求め方①
sin、cosの積がなく、相互関係や2倍角の公式で式変形できるなら2次関数で解け!
個人的には混乱を防ぐため、2次関数で解くときはsinやcosをtとおくのがおすすめ!
Step①:2次関数の形に変換する
三角関数の相互関係、\(\small \sin^2\theta+ \cos^2\theta=1\)より、
$$
\begin{equation}
\begin{split}
&y=\sin^2\theta+\cos\theta+2\\
&y=(1-\cos^2\theta)+\cos\theta+2\\
&y=-\cos^2\theta+\cos\theta+3\\
\end{split}
\end{equation}
$$
ここで、\(\small t=\cos\theta\)とおくと、与式は、\(\small y=-t^2+t+3\)の2次関数とみなすことができ、2次関数の最大最小を求めれる問題に置き換わります。
Step②:\(\small t\)の範囲を求める
ただし、忘れてはいけないのが\(\small t=\cos\theta\)とおいた時の\(\small t\)の取り得る範囲です。\(\small \cos \theta\)は\(\small 0≦\theta<2\pi\)の範囲では-1~1の値をとります(以下の単位円を参照)。なので、\(\small t\)の取り得る範囲も、\(\small \color{red}{ -1≦t≦1}\)となります。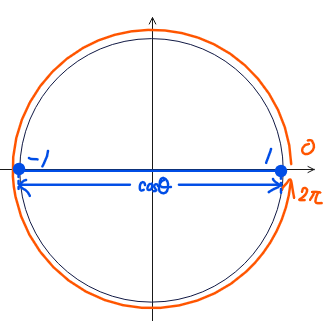
Step③:2次関数の最大最小を求める
あとは、\(\small y=-t^2+t+3\)\(\small (-1≦t≦1)\)のグラフは、軸が\(\small t=-\frac{1}{2\cdot(-1)}=\frac{1}{2}\)、上に凸のグラフであることに注意すると、ざっくりこんなグラフになります。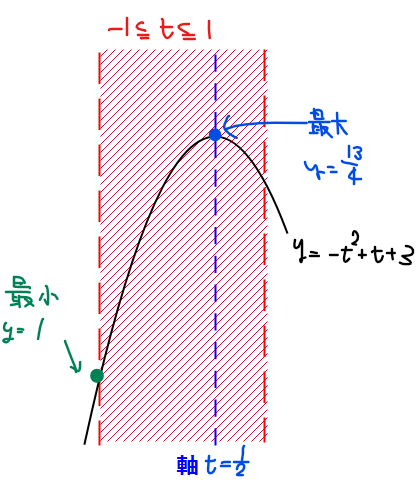
定義域\(\small -1≦t≦1\)の真ん中より右側に軸\(\small t=\frac{1}{2}\)があるので、最小値は軸からより離れている定義域左端(\(\small t=-1\))になります。最大値は頂点ですね。
それぞれの最大値、最小値の値は、\(\small t\)の値を\(\small y=-t^2+t+3\)に代入すれば計算できます。
結果だけまとめると、
\(\small t=\frac{1}{2}\)のとき、最大値\(\small \frac{13}{4}\)、
\(\small t=-1\)のとき、最小値\(\small 1\)
となります。
Step④:\(\small \theta\)の値を求める
「これが解答だ!」と思った人は要注意。赤字の「t=…」の部分が自分で置いた文字tのままになっています。もともと、\(\small t=\cos\theta\)とおいてたので、ここから\(\small \theta\)の値も求めてあげないといけません…。もうひと踏ん張り頑張りましょう!
■\(\small t=\dfrac{1}{2}\)のとき
\(\small \cos\theta=\dfrac{1}{2}\)なので、\(\small 0≦\theta<2\pi\)の範囲で単位円を描いて考えると、\(\small \color{red}{\theta=\dfrac{\pi}{3},\dfrac{5}{3}\pi\space\cdots①}\)となります。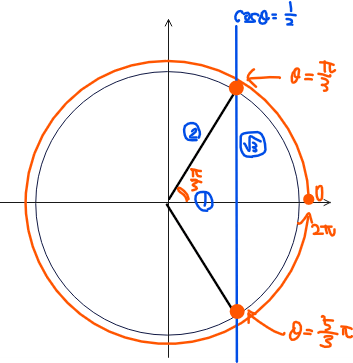
(補足)
単位円上ではcosはx座標なのでx座標が\(\small \frac{1}{2}\)の部分(青線箇所)と単位円との交点での角度が求める\(\small \theta\)になります。
■\(\small t=-1\)のとき
\(\small \cos\theta=-1\)なので、同様に単位円を描いて考えると\(\small \color{red}{\theta=\pi\space\cdots②}\)です。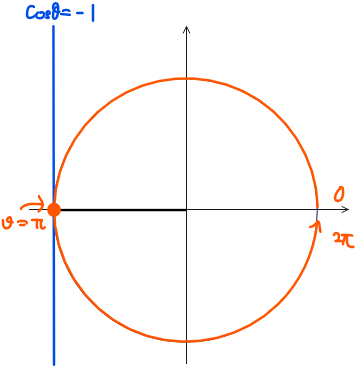
よって、①、②の結果を踏まえて解答は以下になります。
(解答)
\(\small \theta=\dfrac{\pi}{3}、\dfrac{5}{3}\pi\) のとき、最大値 \(\small \dfrac{13}{4}\)、
\(\small \theta=\pi\) のとき、最小値 \(\small 1\).
パターン②:三角関数の合成で解く
sinとcosの足し算、引き算になっていて、角度部分が揃っているような場合に有効な解き方です。三角関数の合成では、単位円を用いて最大値、最小値を求めます。
(1) \(\small y=\sin\theta+\cos\theta\)(\(\small 0≦\theta<2\pi\))
(2) \(\small y=\sin2\theta-\cos2\theta\)\(\small \space\left( 0≦\theta≦\frac{\pi}{2} \right)\)
(3) \(\small y=\sin\theta+2\cos\theta\)\(\small \space\left( 0≦\theta≦\frac{\pi}{2} \right)\)
■三角関数の最大値・最小値の求め方②
sin、cosの積がなく、2次関数にできなさそうなら三角関数の合成で解け!
「三角関数の合成の方法が分からない…」という人は、三角関数の合成公式の証明と使い方を分かりやすく解説で合成公式と使い方を解説しているので参考にしてみてください!
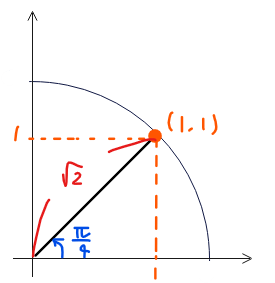
三角関数の合成をすると、\(\small y=\color{red}{\sqrt{2}} \sin\left(\theta\color{blue}{+\dfrac{\pi}{4}}\right)\)。
ここで、角度部分を\(\small \theta+\dfrac{\pi}{4}=t\)とおきます。すると、\(\small y=\sqrt{2} \sin\left(\color{red}{\theta+\dfrac{\pi}{4}}\right)=\sqrt{2}\sin \color{red}t\)。
\(\small t\)の範囲は、
$$
\begin{equation}
\begin{split}
0&≦\theta<2\pi\\
0+\color{blue}{\frac{\pi}{4}} &≦\theta\color{blue}{+\frac{\pi}{4}}<2\pi\color{blue}{+\frac{\pi}{4}}\\
\frac{\pi}{4}&≦\color{red}{\theta+\frac{\pi}{4}}<\frac{9}{4}\pi\\
\frac{\pi}{4}&≦\color{red}t<\frac{9}{4}\pi\quad \cdots①\\
\end{split}
\end{equation}
$$
なので、①の範囲で\(\small y=\sqrt{2}\sin t\)の最大最小を求める問題に置き換えることができました。sinやcos単体の最大値、最小値であれば単位円をかけば求めることができます。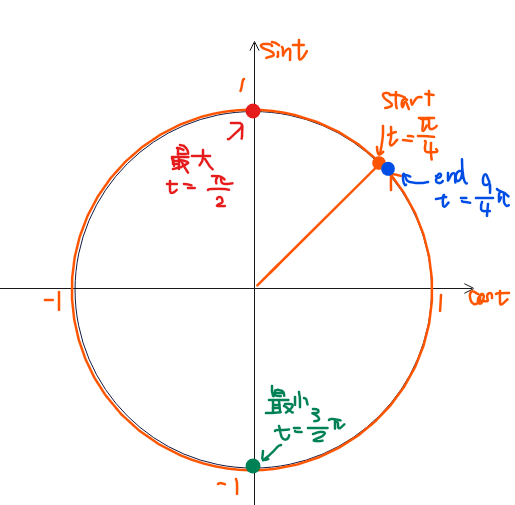
上図のように、まず①の範囲\(\small \color{darkorange}{\dfrac{\pi}{4}≦t<\dfrac{9}{4}\pi}\)をオレンジ色で描きます(スタートが\(\small \dfrac{\pi}{4}\)で、エンドが\(\small \dfrac{9}{4}\pi\)です)。ここが今回考える範囲になります。次に、オレンジ色で塗った範囲で縦軸(\(\small \sin t\))が一番高いところ(=最大)と一番低いところ(=最小)を探します。その時の角度\(\small t\)が最大/最小をとる角度です。
今回であれば、\(\small t=\dfrac{\pi}{2}\)のときに最大、\(\small t=\dfrac{3}{2}\pi\)の時に最小となります。
これらの値を\(\small y=\sqrt{2}\sin t\)に代入することで最大値、最小値を求めることができます。
\(\small t=\dfrac{\pi}{2}\)のとき
$$y=\sqrt{2}\sin \left(\frac{\pi}{2}\right)=\sqrt{2}\cdot 1=\sqrt{2}、$$
\(\small t=\dfrac{3}{2}\pi\)のとき
$$y=\sqrt{2}\sin \left(\frac{3}{2}\pi\right)=\sqrt{2}\cdot (-1)=-\sqrt{2}$$
よって、\(\small t=\dfrac{\pi}{2}\)で、最大値が\(\small \sqrt{2}\)、\(\small t=\dfrac{3}{2}\pi\)で、最小値が\(\small -\sqrt{2}\)となります…②。
最後に、\(\small \theta+\dfrac{\pi}{4}=t\)を使って、\(\small t\)の値を\(\small \theta\)に直せば解答完了です。
■\(\small t=\dfrac{\pi}{2}\)のとき
$$
\begin{equation}
\begin{split}
\theta+\frac{\pi}{4} &=\frac{\pi}{2}\\
\color{red}{\theta} &=\color{red}{\frac{\pi}{4}\quad \cdots③}\\
\end{split}
\end{equation}
$$
■\(\small t=\dfrac{3}{2}\pi\)のとき
$$
\begin{equation}
\begin{split}
\theta+\frac{\pi}{4} &=\frac{3}{2}\pi\\
\color{red}{\theta} &=\color{red}{\frac{5}{4}\pi\quad \cdots④}\\
\end{split}
\end{equation}
$$
よって、②~④を整理すると回答になります。
(解答)
\(\small \theta=\dfrac{\pi}{4}\)のとき、最大値\(\small \sqrt{2}\)、
\(\small \theta=\dfrac{5}{4}\pi\)のとき、最小値\(\small -\sqrt{2}\).
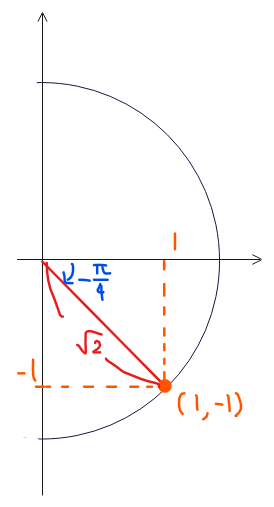
三角関数の合成より、\(\small y=\sin2\theta-\cos2\theta=\color{red}{\sqrt{2}}\sin\left(2\theta\color{blue}{-\dfrac{\pi}{4}}\right)\)。
\(\small 2\theta-\dfrac{\pi}{4}=t\)とおくと、\(\small y=\sqrt{2}\sin t\space\cdots①\)。
\(\small t\)の範囲は、
$$
\begin{equation}
\begin{split}
0&≦\theta≦\frac{\pi}{2}\\
0&≦\color{red}2\theta≦\color{red}2\cdot\frac{\pi}{2}\\
0&≦2\theta≦\pi\\
0\color{blue}{-\frac{\pi}{4}} &≦2\theta\color{blue}{-\frac{\pi}{4}}≦\pi\color{blue}{-\frac{\pi}{4}}\\
-\frac{\pi}{4} &≦2\theta-\frac{\pi}{4}≦\frac{3}{4}\pi\\
-\frac{\pi}{4} &≦t≦\frac{3}{4}\pi\quad\cdots②\\
\end{split}
\end{equation}
$$
よって、②の範囲で式①\(\small y=\sqrt{2}\sin t\)の最大、最小を求めていきます。(1)と同様に、単位円を描いて考えるのがおすすめです。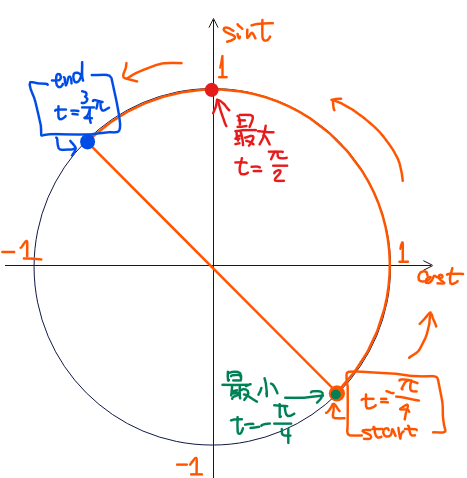
②の範囲は、上図の単位円でいうオレンジ色部分なので、そこで縦軸\(\small \sin t\)が最大になるのは、\(\small t=\dfrac{\pi}{2}\)のときで、最小になるのは\(\small t=-\dfrac{\pi}{4}\)のときと分かります。
よって、\(\small y=\sqrt{2}\sin t\)に代入することで、
\(\small t=\dfrac{\pi}{2}\)のとき、最大値は
$$ y=\sqrt{2}\sin\dfrac{\pi}{2}=\sqrt{2}\cdot1=\color{red}{\sqrt{2}}、$$
\(\small t=-\dfrac{\pi}{4}\)のとき、最小値は
$$ y=\sqrt{2}\sin\left(-\dfrac{\pi}{4}\right)=\sqrt{2}\cdot\left(-\frac{1}{\sqrt{2}}\right)=\color{green}{-1}$$
をとります…③。
最後に、\(\small 2\theta+\dfrac{\pi}{4}=t\)を使って、それぞれの\(\small \theta\)の値を求めます。
■\(\small t=\dfrac{\pi}{2}\)のとき
$$
\begin{equation}
\begin{split}
2\theta-\dfrac{\pi}{4} &=\frac{\pi}{2}\\
2\theta &=\frac{3}{4}\pi\\
\color{red}{\theta} &=\color{red}{\frac{3}{8}\pi\quad \cdots④}\\
\end{split}
\end{equation}
$$
■\(\small t=-\dfrac{\pi}{4}\)のとき
$$
\begin{equation}
\begin{split}
2\theta-\dfrac{\pi}{4} &=-\frac{\pi}{4}\\
2\theta &=0\\
\color{red}{\theta} & \color{red}{=0\quad \cdots⑤}\\
\end{split}
\end{equation}
$$
③~⑤の結果を整理すれば答えになります。
(解答)
\(\small \theta=\dfrac{3}{8}\pi\)のときに、最大値\(\small \sqrt{2}\)、
\(\small \theta=0\)のときに、最大値\(\small -1\).
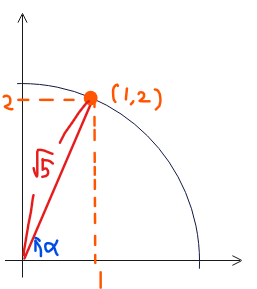
三角関数、\(\small y=\sin\theta+2\cos\theta\)の合成は上図のように角度が分からないので、\(\small \alpha\)とおいておきます。解答で論述するときには、「\(\small \alpha\)は\(\small \sin\alpha=\dfrac{2}{\sqrt{5}}\)、\(\small \cos\alpha=\dfrac{1}{\sqrt{5}}\)を満たす角度とする」…①などと記載しておきましょう。
\(\small \alpha\)を使って合成すると、\(\small y=\color{red}{\sin\theta+2\cos\theta=\sqrt{5}\sin \left(\theta+\alpha\right)}\)となります。
\(\small t=\theta+\alpha\)とおくと、\(\small y=\sqrt{5}\sin \color{red}{\left(\theta+\alpha\right)}=\sqrt{5}\sin \color{red}t \space \cdots②\)。
\(\small t\)の範囲は、
$$
\begin{equation}
\begin{split}
&0≦\theta≦\frac{\pi}{2}\\
&\alpha≦\theta+\alpha≦\frac{\pi}{2}+\alpha \quad \cdots③\\
\end{split}
\end{equation}
$$
③の範囲を単位円上に図示すると以下の通りになります。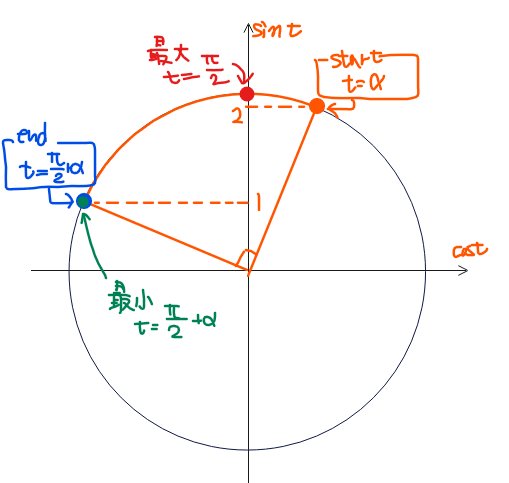
最大となるのは単位円から\(\small t=\dfrac{\pi}{2}\)のときで、式②\(\small y=\sqrt{5}\sin t\)に代入することで、最大値は、
$$ y=\sqrt{5}\sin \dfrac{\pi}{2}=\sqrt{5}\cdot 1=\color{red}{\sqrt{5}}\space \cdots④$$
最小は\(\small t=\alpha\)なのか、\(\small \dfrac{\pi}{2}+\alpha\)なのかちょっと迷うかもしれません。そういう時は、実際に式②に代入して\(\small y\)の値を求めて比較してみればokです。
\(\small \sin\alpha=\dfrac{2}{\sqrt{5}}\)、\(\small \cos\alpha=\dfrac{1}{\sqrt{5}}\)であることを用いると(一番はじめに①で定義したやつ)、
\(\small t=\alpha\)では、
$$ y=\sqrt{5}\sin \alpha=\sqrt{5}\cdot\dfrac{2}{\sqrt{5}}=2、$$
\(\small t=\dfrac{\pi}{2}+\alpha\)では、
$$ y=\sqrt{5}\color{red}{\sin \left(\dfrac{\pi}{2}+\alpha \right)}=\sqrt{5}\color{red}{\cos\alpha}=\sqrt{5}\cdot\dfrac{1}{\sqrt{5}}=1.$$
赤字箇所は、三角比の基本公式ですが覚えていなくても加法定理で導けます。このあたりの細かい公式については「三角比の基本公式の効率な覚え方(180°±θ、90°±θなど全パターンを解説)」で解説しているのでよかったら読んでみてください!
脱線しましたが、\(\small y\)の値を比較すると\(\small t=\dfrac{\pi}{2}+\alpha\)の方が値が小さいので、\(\small t=\dfrac{\pi}{2}+\alpha\)で最小値が\(\small y=1\space \cdots⑤\)になります。
④、⑤の結果をまとめると、\(\small t=\dfrac{\pi}{2}\)のとき最大値\(\small \sqrt{5}\)、\(\small t=\dfrac{\pi}{2}+\alpha\)のとき最小値\(\small 1\)をとることが分かりました。
最後に、\(\small \theta+\alpha=t\)を使って、\(\small t\)の値から\(\small \theta\)の値を求めます。
■\(\small t=\dfrac{\pi}{2}\)のとき
$$
\begin{equation}
\begin{split}
\theta+\alpha &=\frac{\pi}{2}\\
\theta &=\frac{\pi}{2}-\alpha\\
\end{split}
\end{equation}
$$
\(\small \theta\)について解きましたが、これだと\(\small \theta\)の値を表すのに自分で置いた\(\small \alpha\)が入ってしまうので、回答としては微妙です。もちろん、\(\small \alpha\)の値は求められないので、そういう時は、\(\small \theta\)の代わりに\(\small \sin \theta\)、\(\small \cos \theta\)の値で答えるのがよいと思います。
\(\small \theta=\dfrac{\pi}{2}-\alpha\)より、
$$
\begin{equation}
\begin{split}
\color{red}{\sin \theta}&=\sin \left( \frac{\pi}{2}-\alpha\right)\\
&=\cos\alpha\\
&=\color{red}{\frac{1}{\sqrt{5}}}\quad \cdots ⑥\\
\end{split}
\end{equation}
$$
$$
\begin{equation}
\begin{split}
\color{red}{\cos \theta}&=\cos \left( \frac{\pi}{2}-\alpha\right)\\
&=\sin\alpha\\
&=\color{red}{\frac{2}{\sqrt{5}}}\quad \cdots ⑦\\
\end{split}
\end{equation}
$$
■\(\small t=\dfrac{\pi}{2}+\alpha\)のとき
$$
\begin{equation}
\begin{split}
\theta+\alpha &=\frac{\pi}{2}+\alpha\\
\color{red}{\theta} &=\color{red}{\frac{\pi}{2}}\quad \cdots ⑧\\
\end{split}
\end{equation}
$$
④、⑤の最大値、最小値と⑥~⑧の\(\small \theta\)の値を整理すれば解答です。
(解答)
\(\small \sin \theta=\dfrac{1}{\sqrt{5}}\)、\(\small \cos \theta=\dfrac{2}{\sqrt{5}}\)のとき、最大値\(\small \sqrt{5}\)、
\(\small \theta=\dfrac{\pi}{2}\)のとき、最小値\(\small 1\).
パターン③:2倍角の公式で次数下げして解く
また、そのときの\(\small \theta\)の値を求めよ。
■三角関数の最大値・最小値の求め方③
sin、cosの積があり、sin、cosの2乗があれば2倍角の公式で三角関数の合成(パターン②)に帰着させろ!
2倍角の公式を以下のように逆に使うことで、sinやcosの2乗、sinとcosの積を単純なsinとcosに置き換えることができます(ちょっと難しくに言うなら「次数下げ」ができます…)。
■2倍角の公式 ~いつもと逆ver~
$$
\begin{equation}
\begin{split}
&\sin\theta \cos\theta=\frac{1}{2} \sin2\theta\\
&\sin^2\theta=\frac{1-\cos2\theta}{2}\\
&\cos^2\theta=\frac{1+\cos2\theta}{2}\\
\end{split}
\end{equation}
$$
置き換えた後は、sinとcosの足し算・引き算になるので、パターン②の三角関数の合成で解くことができます。
\(\small y=\sin^2\theta-\sqrt{3}\sin\theta\cos\theta+2\cos^2\theta\)は
$$
\begin{equation}
\begin{split}
&\sin\theta \cos\theta=\frac{1}{2} \sin2\theta\\
&\sin^2\theta=\frac{1-\cos2\theta}{2}\\
&\cos^2\theta=\frac{1+\cos2\theta}{2}\\
\end{split}
\end{equation}
$$
を用いることで、
$$
\begin{equation}
\begin{split}
&y=\color{blue}{\sin^2\theta}-\sqrt{3}\color{green}{\sin\theta\cos\theta}+2\color{darkorange}{\cos^2\theta}\\
&y=\color{blue}{\frac{1-\cos2\theta}{2}}-\sqrt{3}\cdot\color{green}{\frac{1}{2} \sin2\theta}+2\cdot\color{darkorange}{\frac{1+\cos2\theta}{2}}\\
&y=\color{red}{-\frac{\sqrt{3}}{2} \sin2\theta+\frac{1}{2}\cos2\theta}+\frac{3}{2}\\
\end{split}
\end{equation}
$$
以降は、パターン②の解き方と同じです。赤字部分を三角関数の合成公式でまとめると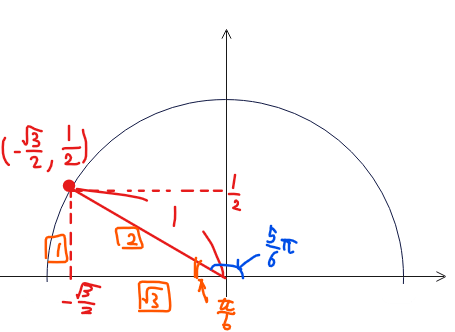
$$
\begin{equation}
\begin{split}
&y=\color{red}{\sin \left(2\theta+\frac{5}{6}\pi\right)}+\frac{3}{2}\quad \cdots ①.\\
\end{split}
\end{equation}
$$
sin、cosの係数が分数になっていてややこしいですが、上記のように三角形の辺の比(オレンジ色の四角)で考えれば半径も、角度も求まります。
\(\small t=2\theta+\dfrac{5}{6}\pi\)とおきます。\(\small t\)の範囲は
$$
\begin{equation}
\begin{split}
0&≦\theta≦\frac{\pi}{2}\\
0&≦2\theta≦\pi\\
\color{red}{\frac{5}{6}\pi} &≦2\theta\color{red}{+\frac{5}{6}\pi}≦\pi\color{red}{+\frac{5}{6}\pi}\\
\frac{5}{6}\pi &≦t≦\frac{11}{6}\pi \quad \cdots ②\\
\end{split}
\end{equation}
$$
①の式は、
$$y=\color{red}{\sin t}+\frac{3}{2}\quad \cdots③$$
となるので、あとは、②の範囲で\(\small \sin t\)の最大、最小が分かればokです。
単位円をかくと、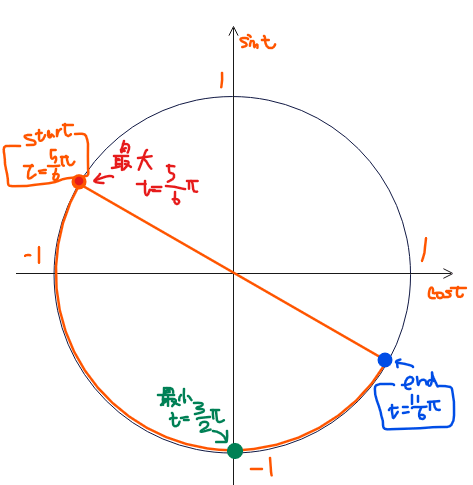
なので、\(\small t=\dfrac{5}{6}\pi\)で最大、\(\small t=\dfrac{3}{2}\pi\)で最小となることが分かります。
あとは、それぞれの最大値、最小値は、式③\(\small y=\sin t+\dfrac{3}{2}\)に代入すれば求めることができ、
\(\small t=\dfrac{5}{6}\pi\)のとき、最大値は
$$ y=\sin\left(\frac{5}{6}\pi\right)+\frac{3}{2}=\frac{1}{2}+\frac{3}{2}=\color{red}2\quad \cdots④$$
\(\small t=\dfrac{3}{2}\pi\)のとき、最小値は
$$ y=\sin\left(\frac{3}{2}\pi\right)+\frac{3}{2}=-1+\frac{3}{2}=\color{red}{\frac{1}{2}}\quad \cdots⑤$$
最後に、\(\small t\)の値から\(\small \theta\)を求めます。\(\small t=2\theta+\dfrac{5}{6}\pi\)とおいていたので、
\(\small t=\dfrac{5}{6}\pi \)のとき
$$
\begin{equation}
\begin{split}
\frac{5}{6}\pi &=2\theta+\frac{5}{6}\pi\\
2\theta&=0\\
\color{red}{\theta} & \color{red}{= 0}\quad \cdots⑥\\
\end{split}
\end{equation}
$$
\(\small t=\dfrac{3}{2}\pi \)のとき
$$
\begin{equation}
\begin{split}
\frac{3}{2}\pi &=2\theta+\frac{5}{6}\pi\\
2\theta &=\frac{3}{2}\pi-\frac{5}{6}\pi\\
2\theta &=\frac{2}{3}\pi\\
\color{red}{\theta} & \color{red}{= \frac{\pi}{3}}\quad \cdots⑦\\
\end{split}
\end{equation}
$$
よって、④~⑦の結果を整理すれば答えになります。
(解答)
\(\small \theta=0\)のとき、最大値2、
\(\small \theta=\dfrac{\pi}{3}\)のとき、最小値\(\small \dfrac{1}{2}\)
パターン④:\(\small x= \sin\theta+ \cos\theta\)とおいて解く
また、そのときの\(\small \theta\)の値を求めよ。
■三角関数の最大値・最小値の求め方④
sin、cosの積があり、パターン③以外かつsin、cosの対称式なら、\(\small x= \sin\theta+ \cos\theta\)とおいて2次関数の最大最小(パターン①)に帰着させろ!
\(\small xy+x+y+1\)や\(\small x^2-2xy+y^2\)のように2種類の文字を入れ替えても式の見た目が変わらない式のことを対称式といいます。
たとえば、\(\small xy+x+y+1\)であれば、\(\small x\)と\(\small y\)を入れ替えると\(\small yx+y+x+1=xy+x+y+1\)のように並べ替えると元の式と同じになるので対称式となるわけです。
逆に、\(\small xy+x-y+1\)は、入れ替えると\(\small yx+y-x+1=xy-x+y+1\)となり、\(\small x,y\)の係数が元の式と一致しないので対称式ではありません。
\(\small x= \sin\theta+ \cos\theta\)とおきます。文字で置いたら、まずは\(\small x\)の範囲を求めておきましょう。
■\(\small x\)の取り得る値の範囲
三角関数の合成を用いると
$$x=\sin\theta+ \cos\theta=\sqrt{2}\sin\left(\theta+\frac{\pi}{4}\right)$$
\(\small \alpha=\theta+\dfrac{\pi}{4}\)とおくと、
$$x=\sqrt{2}\sin\left(\color{red}{\theta+\frac{\pi}{4}}\right)=\sqrt{2}\sin\color{red}\alpha\quad \cdots ①$$
\(\small 0≦\theta≦\pi\)より、
$$
\begin{equation}
\begin{split}
&0≦\theta≦\pi\\
&\color{blue}{\frac{\pi}{4}}≦\theta\color{blue}{+\frac{\pi}{4}}≦\pi\color{blue}{+\frac{\pi}{4}}\\
&\frac{\pi}{4}≦\alpha≦\frac{5}{4}\pi\quad\cdots②\\
\end{split}
\end{equation}
$$
②の範囲で①\(\small x=\sqrt{2}\sin \alpha\)の最大、最小を考えると、以下の単位円から
\(\small \alpha=\dfrac{\pi}{2}\)のとき、最大値\(\small x=\sqrt{2}\sin\color{red}\alpha=\sqrt{2}\sin\left(\color{red}{\dfrac{\pi}{2}}\right)=\color{red}{\sqrt{2}}\)、
\(\small \alpha=\dfrac{5}{4}\pi\)のとき、最小値\(\small x=\sqrt{2}\sin\color{green}\alpha=\sqrt{2}\sin\left(\color{green}{\dfrac{5}{4}\pi}\right)=\sqrt{2}\cdot\left(-\dfrac{1}{\sqrt{2}}\right)=\color{green}{-1}\)
と求まります。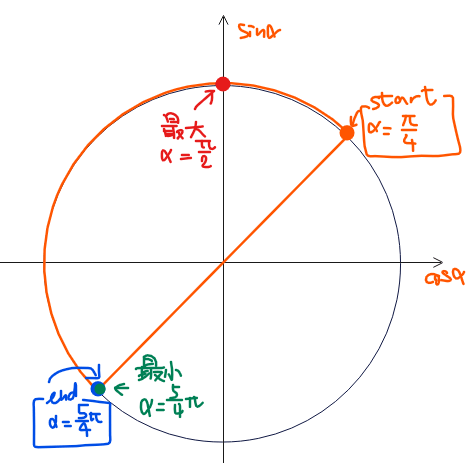
よって、\(\small x\)の範囲は、
$$\color{red}{-1≦x≦\sqrt{2}\quad \cdots ③}$$
となります。
■\(\small x\)で置き換えて、2次関数にする
では、ここからが本題、\(\small y=\sin\theta \cos\theta-\sin\theta-\cos\theta+2\)を\(\small x\)を使って表していきます。
$$
\begin{equation}
\begin{split}
&x=\sin\theta+\cos\theta\\
&x^2=(\sin\theta+\cos\theta)^2\\
&x^2=\color{red}{\sin^2\theta}+2\sin\theta\cos\theta+\color{red}{\cos^2\theta}\\
&x^2=\color{red}{1}+2\sin\theta\cos\theta\\
&x^2-1=2\sin\theta\cos\theta\\
&\frac{x^2-1}{2}=\sin\theta\cos\theta\\
\end{split}
\end{equation}
$$
この関係式を使うと、\(\small \sin\theta\cos\theta\)の積を\(\small x\)を使って表すことができます。
つまり、問題の式は、
$$
\begin{equation}
\begin{split}
&y=\sin\theta \cos\theta-\sin\theta-\cos\theta+2\\
&y=\color{red}{\sin\theta \cos\theta}-(\color{blue}{\sin\theta+\cos\theta})+2\\
&y=\color{red}{\frac{x^2-1}{2}}-\color{blue}{x}+2\\
&y=\frac{1}{2}x^2-x+\frac{3}{2} \quad \cdots ④\\
\end{split}
\end{equation}
$$
となり、2次関数になります。ただし、赤字部分は先程求めた
$$\color{red}{\sin\theta\cos\theta=\frac{x^2-1}{2}}、$$
青字部分は今回のポイントである
$$\color{blue}{x=\sin\theta+ \cos\theta}$$
の関係を使っています。
ここまでの結果を整理すると、\(\small x=\sin\theta+ \cos\theta\)とおくことで\(\small y=\sin\theta \cos\theta-\sin\theta-\cos\theta+2\)の最大最小問題は、③、④の結果から、\(\small y=\dfrac{1}{2}x^2-x+\dfrac{3}{2}\space(-1≦x≦\sqrt{2})\)の最大最小を求める問題に置き換えることができました。
■2次関数の最大最小を求める
ここからは、パターン①のStep③以降の解き方と同じ要領で解くことができます。
\(\small y=\dfrac{1}{2}x^2-x+\dfrac{3}{2}\space(-1≦x≦\sqrt{2})\)のグラフの軸は、
$$x=-\frac{(-1)}{2\cdot\left(\frac{1}{2}\right)}=1$$
なのでグラフの概略と最大、最小をとるポイントは以下の通り。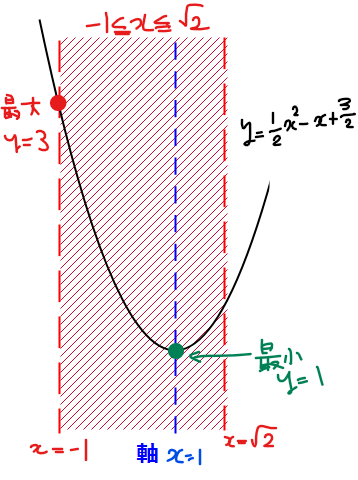
よって、\(\small x=-1\)で最大値\(\small 3\)、\(\small x=1\)で最小値\(\small 1\)…⑤をとります。
■\(\small x\)の値から\(\small \theta\)の値を求める
一番はじめに、\(\small x=\sqrt{2}\sin\left(\theta+\dfrac{\pi}{4}\right)=\sqrt{2}\sin \alpha\)(ただし、\(\small \alpha=\theta+\dfrac{\pi}{4}\))という変形をしているので、この式を使ってまず\(\small \alpha\)を求め、そのあとに\(\small \theta\)の値を求めていきます。
■\(\small x=-1\)のとき
$$
\begin{equation}
\begin{split}
\color{blue}x &=\sqrt{2}\sin\alpha\\
\sqrt{2}\sin\alpha &=\color{blue}{-1}\\
\sin\alpha &=-\frac{1}{\sqrt{2}}\\
\end{split}
\end{equation}
$$
この式を満たす\(\small \alpha\)の値は、式②で求めた\(\small \alpha\)の範囲\(\small \left( \dfrac{\pi}{4}≦\alpha≦\dfrac{5}{4}\pi \right)\)に注意して単位円上で考えると、解になるのは下図でいうと\(\small \alpha\)の範囲であるオレンジ箇所と、今考えている方程式である青線の交点なので、\(\small \alpha=\dfrac{5}{4}\pi\)となります(青点箇所)。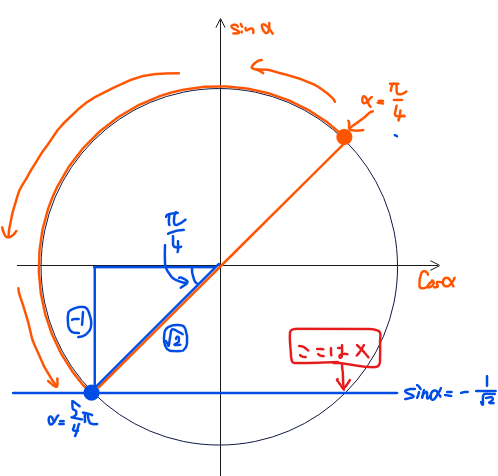
補足として、図中の赤字「ここは×」も、青線と単位円の交点ですが、今回考えているオレンジの範囲外なので、解としては不適になります。
よって、\(\small \alpha=\theta+\dfrac{\pi}{4}\)の関係式に\(\small \alpha=\dfrac{5}{4}\pi\)を代入して\(\small \theta\)を求めると、
$$
\begin{equation}
\begin{split}
\frac{5}{4}\pi &=\theta+\frac{\pi}{4}\\
\color{red}{\theta} &\color{red}{=\pi \quad \cdots⑥}\\
\end{split}
\end{equation}
$$
■\(\small x=1\)のとき
$$
\begin{equation}
\begin{split}
x &=\sqrt{2}\sin\alpha\\
\sqrt{2}\sin\alpha &=1\\
\sin\alpha &=\frac{1}{\sqrt{2}}\\
\end{split}
\end{equation}
$$
同様に、この式を満たす\(\small \alpha\)を単位円上の\(\small \dfrac{\pi}{4}≦\alpha≦\dfrac{5}{4}\pi\)の範囲で考えると、下図の青点の2か所があるので、\(\small \alpha=\dfrac{\pi}{4}、\dfrac{3}{4}\pi\)の2つが解になります。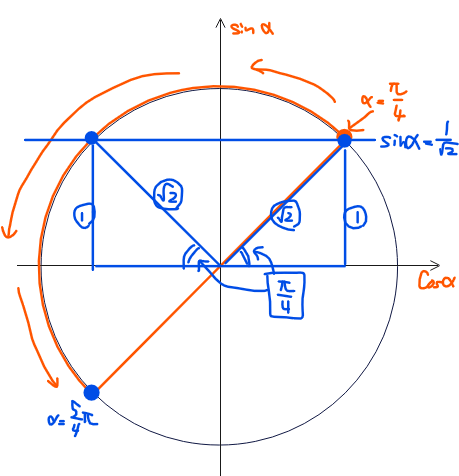
あとは\(\small \alpha=\theta+\dfrac{\pi}{4}\)に、今求めた\(\small \alpha\)をそれぞれ代入して\(\small \theta\)を求めると、
$$
\begin{equation}
\begin{split}
\frac{\pi}{4} &=\theta+\frac{\pi}{4}\\
\color{red}{\theta} &=\color{red}{0\quad \cdots⑦}、\\
&\\
\frac{3}{4}\pi &=\theta+\frac{\pi}{4}\\
\color{red}{\theta} &=\color{red}{\frac{\pi}{2}\quad \cdots⑧}\\
\end{split}
\end{equation}
$$
よって、⑤の最大値、最小値と⑥~⑧の\(\small \theta\)の値を整理すれば答えになります。
(解答)
\(\small \theta=\pi\) のとき、最大値 3、
\(\small \theta=0、\dfrac{\pi}{2}\) のとき、最小値 1.
パターン⑤:図形的に解く
sinとcosを含む分数の形になっているときに有効な解き方です。ここでは、円と1次関数の交点を考えることで図形的に解くことができる方法を解説します。
使用頻度は高くないですが、知っておくと便利です。重要度は低いため、三角関数が苦手という人は一旦飛ばしてしまってもokだと思います。
また、そのときの\(\small \theta\)の値を求めよ。
■三角関数の最大値・最小値の求め方⑤
分数型は、円と直線の図を描いて、直線の傾きの最大、最小の問題に置き換えることができる。
方程式の最大、最小の問題を直線の傾きを利用して図形的に解く問題を「線形計画法」といいます。三角関数が分数になっていれば必ず線形計画法で解けるという万能な手法ではないですが、意外と使えるので紹介します。
ちなみに、分数型で線形計画法で解けない場合は、微分などを使って解くことになります。
\(\small X=\cos\theta、Y=\sin\theta\)とおくと、
$$
\begin{equation}
\begin{split}
&\sin^2\theta+\cos^2\theta=1\\
\Leftrightarrow \space &X^2+Y^2=1\quad \cdots ①\\
\end{split}
\end{equation}
$$
なので、点\(\small( X、Y)\)は原点を中心とした半径1の円上の点を表します。
さらに、\(\small 0≦\theta≦\pi\)の範囲では、\(\small X、Y\)は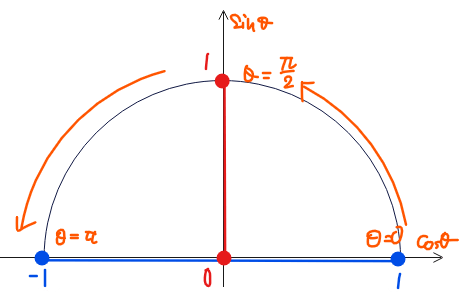
$$
\begin{equation}
\begin{split}
&\color{blue}{-1≦X≦1}、\color{red}{0≦Y≦1}\quad \cdots ②\\
\end{split}
\end{equation}
$$
の値しかとれないことを加味すると、点\(\small ( X、Y)\)は原点を中心とした半径1の円周の上半分上の点になります。
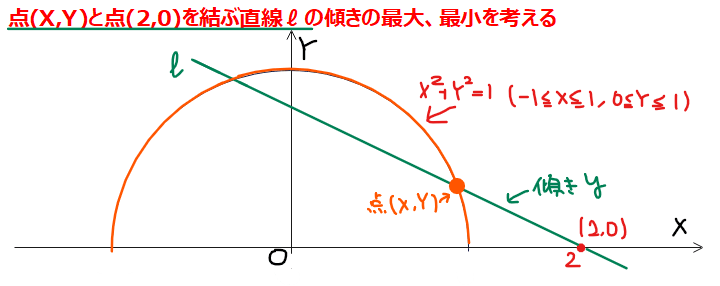
問題の式、\(\small y=\dfrac{\sin\theta}{\cos\theta-2}\)は、
$$y=\dfrac{Y}{X-2}$$
となるので、「\(\small Y=\cdots\)」の形に直すと
$$Y=y(X-2) \quad \cdots ③$$
上式は、\(\small XY\)平面上で、傾きが\(\small y\)で点\(\small (2,0)\)を通る直線の方程式を表しています。
(補足)
点\(\small (a,b)\)を通り、傾き\(\small m\)の直線の方程式は
$$y=m(x-a)+b$$
ここまでの内容を整理すると、もともとの問題である、
『\(\small 0≦\theta≦\pi\)のとき、\(\small y=\dfrac{\sin\theta}{\cos\theta-2}\)の最大値、最小値を求める』
ということは、
『原点を中心とした半径1の円周の上半分上の点\(\small( X、Y)\)のうち、\(\small y\)の最大値、最小値を求める』、
↓
『原点を中心とした半径1の円周の上半分上の点\(\small \color{darkorange}{( X、Y)}\)のうち、点\(\small (2,0)\)を通る直線の傾き\(\small y\)の最大値、最小値を求める』
という問題を考えることと同じになります。
緑線ℓの傾きが最大、最小となるような箇所を探すことでもともとの三角関数の最大最小が求まる。
ゆえに、図形的な問題として解くことができ、下図から傾きが最小となるのが[A]、傾きが最大となるのが[B]であることが分かります。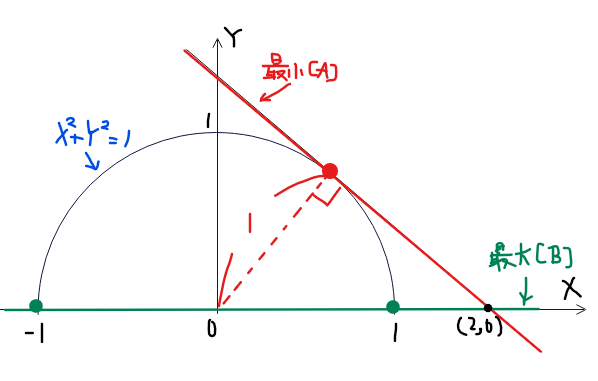
(補足)
今回は傾きが負なので、「傾きが急なほど値は小さくなる(傾きが-2よりも-10の方が急→-10の方が値としては小さい)」という点だけ注意です。
■[A]の場合
円:\(\small X^2+Y^2=1\)と直線:\(\small Y=yX-2y⇔yX-Y-2y=0\)が接するときなので、原点と直線:\(\small yX-Y-2y=0\)との距離が1であることから、点と直線の距離の公式を使って
$$
\begin{equation}
\begin{split}
\frac{|y\cdot0-0-2y|}{\sqrt{y^2+(-1)^2}} &=1\\
\frac{|-2y|}{\sqrt{y^2+1}} &=1\\
|-2y| &=\sqrt{y^2+1}\\
\end{split}
\end{equation}
$$
絶対値が邪魔なので両辺を2乗することで
$$
\begin{equation}
\begin{split}
(|-2y|)^2 &=\left(\sqrt{y^2+1}\right)^2\\
4y^2 &=y^2+1\\
3y^2 &=1\\
y^2 &=\frac{1}{3}\\
y &=\pm \frac{1}{\sqrt{3}}\\
\end{split}
\end{equation}
$$
\(\small y\)は直線の方程式の傾きを表していたので、図形から明らかに(傾き)<0。
よって、\(\small y=-\dfrac{1}{\sqrt{3}}\)が最小値…④。
このときの\(\small \theta\)の値は、式③に\(\small y\)を代入して
$$
\begin{equation}
\begin{split}
&Y =-\frac{1}{\sqrt{3}}(X-2)\\
&-\sqrt{3}Y =X-2\\
&X+\sqrt{3}Y =2\\
\end{split}
\end{equation}
$$
より、\(\small X=\cos\theta、Y=\sin\theta\)を代入して
$$
\begin{equation}
\begin{split}
\sqrt{3}\sin\theta+&\cos\theta =2\\
\end{split}
\end{equation}
$$
三角関数の合成を使うことで、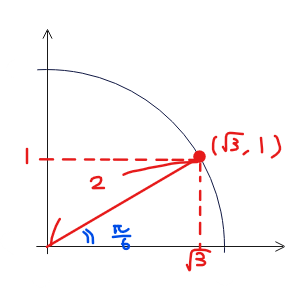
$$
\begin{equation}
\begin{split}
\color{red}2\sin\left(\theta+\color{blue}{\frac{\pi}{6}}\right) &=2\\
\sin\left(\theta+\frac{\pi}{6}\right) &=1\\
\end{split}
\end{equation}
$$
\(\small t=\theta+\dfrac{\pi}{6}\)とおくと、\(\small \sin t= 1\)。\(\small t\)の範囲は、
$$
\begin{equation}
\begin{split}
&0≦\theta≦\pi\\
&\color{red}{\frac{\pi}{6}}≦\theta \color{red}{+\frac{\pi}{6}}≦\pi\color{red}{+\frac{\pi}{6}}\\
&\frac{\pi}{6}≦t≦\frac{5}{6}\pi\\
\end{split}
\end{equation}
$$
よって、\(\small \color{darkorange}{\dfrac{\pi}{6}≦t≦\dfrac{5}{6}\pi}\)の範囲で\(\small \color{red}{\sin t=1}\)を満たす\(\small t\)の値は、単位円から、\(\small t=\dfrac{\pi}{2}\)。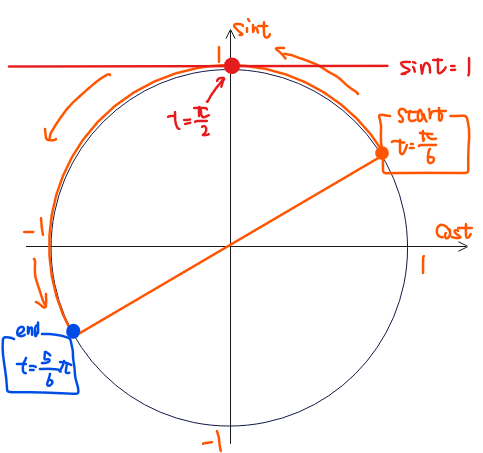
\(\small t=\theta+\dfrac{\pi}{6}\)なので、
$$
\begin{equation}
\begin{split}
\frac{\pi}{2}&=\theta+\dfrac{\pi}{6}\\
\theta&=\frac{\pi}{2}-\dfrac{\pi}{6}\\
\color{red}{\theta} &\color{red}{=\frac{\pi}{3}}\quad \cdots⑤\\
\end{split}
\end{equation}
$$
④、⑤より、\(\small \theta=\dfrac{\pi}{3}\)のとき、最小値 \(\small -\dfrac{1}{\sqrt{3}}\)。
■[B]の場合
傾きが0なので、最大値は、\(\small y=0\)。このとき、式③は
$$
\begin{equation}
\begin{split}
&0=\frac{Y}{X-2}\\
\end{split}
\end{equation}
$$
なので、
$$
\begin{equation}
\begin{split}
&Y=0\\
\end{split}
\end{equation}
$$
\(\small Y=\sin\theta\)なので、\(\small \sin\theta=0\)。\(\small 0≦\theta≦\pi\)の範囲でsinが0になる点は\(\small \theta=0、\pi\)のとき。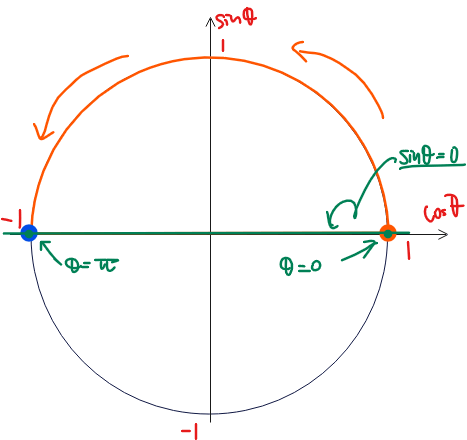
よって、\(\small \theta=0、\pi\)のとき、最大値 0。
(解答)
\(\small \theta=\dfrac{\pi}{3}\) のとき、最小値 \(\small -\dfrac{1}{\sqrt{3}}\)、
\(\small \theta=0、\pi\) のとき、最大値 0。
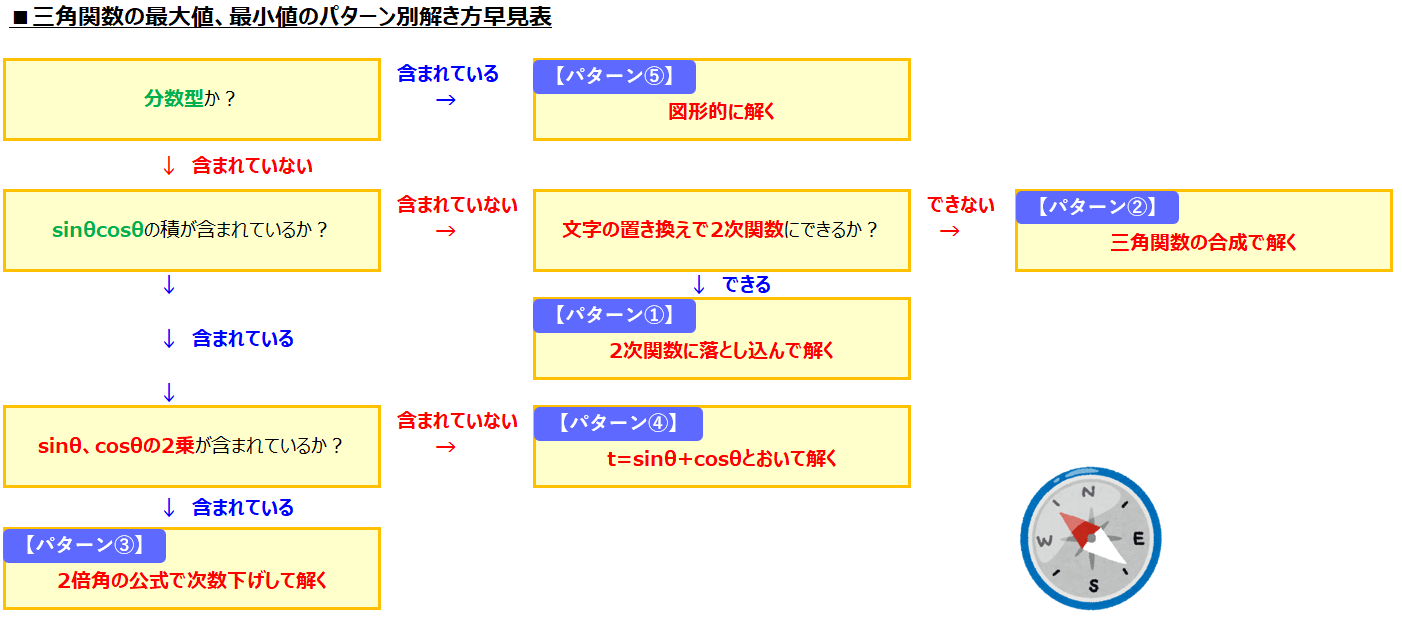
各種問題パターンの見分け方
ここまで、5パターンの解法を解説してきました。実際に問題を解くときには、その問題がどのパターンなのかを見極める必要があります。最後に、パターンの見分け方のコツを整理したので参考にしてみてください。
まとめ
今回は、パターンごとに三角関数の最大値、最小値の求め方について解説しました。
ほとんどの問題は今回紹介した5パターンのどれかに当てはまるので、これだけ覚えておけば三角関数の最大値、最小値の問題で解き方に躓くことはないと思うので、しっかり復習してマスターしておきましょう!
■三角関数の最大値、最小値の解法パターン5選
- 2次関数に落とし込んで解く
- 三角関数の合成で解く
- 2倍角の公式で次数下げして解く
- \(\small t= \sin\theta+ \cos\theta\)とおいて解く
- 図形的に解く

本日はここまでです。お疲れさまでした!







コメント