【数Ⅲ_極限】中間値の定理とは？定理の直感的な解釈と入試問題への応用

今回は中間値の定理について解説していきます。そもそも中間値の定理とは、以下のような定理となっています。

Point：中間値の定理

関数$\small f(x)$が閉区間 $\small [a,b]$で連続、かつ$\small f(a) \neq f(b)$ならば、$\small f(a)$と$\small f(b)$の間の任意の値 $\small k$に対して $$\small f(c)=k \quad (a < c < b)$$ を満たすような実数$\small c$が存在する。

文字だけ読んでも何を言っているのか非常にわかりにくいですよね(^^;)。

そこで本記事では、中間値の定理の内容を数学初心者にも直感的にわかりやすい言葉で解説していきます。そのうえで、中間値の定理がどのように使えるのかについても、実際の入試問題を通して解説していきますので、是非最後まで一緒に確認していきましょう！

　本記事はこんな人におすすめ

中間値の定理を直感的に理解したい人
中間値の定理の使いどころが知りたい人
中間値の定理を利用した問題演習をしたい人、実践的な力をアップさせたい人
大学入試対策、定期テスト対策がしたい人

　本記事のレベル

重要度

低

余力あれば

普通

必須

高
難易度

易しい

易

やや易

やや難

難

難しい
暗記/理解

暗記重視

暗記

半々

理解

理解重視

【基礎講義】中間値の定理とは
1. 【講義1】中間値の定理を分かりやすく翻訳しよう
2. 【講義2】頻出！中間値の定理の使い方
【問題＆解説】中間値の定理を利用した問題
本記事のまとめ

【基礎講義】中間値の定理とは

【講義1】中間値の定理を分かりやすく翻訳しよう

改めまして中間値の定理とは数学的に以下のように表現されます。

Point：中間値の定理

うん…、で、どゆこと？という声が聞こえてきそうなので、まずは用語の意味も含めて文章の意味を1つずつ確認していきましょう。

分かりにくいポイント①：閉区間 $\small [a,b]$で連続
閉区間 $\small [a,b]$とは、$\small a ≦ x ≦ b$のことです。閉区間の範囲を数直線で表すと下図のように端点が黒丸で表現されることから、「閉じた区間」というイメージをすれば分かりやすいでしょう。逆に、開区間は $\small (a,b)$と表され、$\small a < x < b$のことです。数直線上ではその範囲の端点が白丸で表現されることから、「開いた区間」というイメージで開区間となります。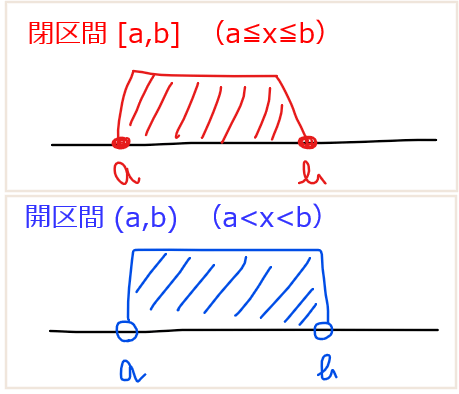

連続については、詳細は「【数Ⅲ_極限】関数の連続性とは？右側極限・左側極限を用いた問題の解き方・考え方を完全攻略！」の記事で解説していますが、ここでは「曲線がつながっている（途切れていない）」という意味だということを押さえておけば大丈夫です！

分かりにくいポイント②：$\small f(a)$と$\small f(b)$の間の任意の値…（以下省略）
はじめて中間値の定理に触れた人には後半部分が特に難解だと思います。ここで言っていることの要点だけを一言でざっくりまとめるならば、2点間に直線を引いたら必ず関数$\small f(x)$と交わるということを言っています。では、どうしてそのような解釈ができるかもう少し詳しく解説します。
関数の世界では横一直線の関数は定数関数 $\small y=k$（$\small k$は定数）で表現されます。そして横直線と関数 $\small f(x)$との交点は $\small f(x)=k$の方程式を解くことで求めることができます。この方程式の解が $\small x=c$であれば、交点の$\small x$座標が$\small c$となります（下図参照）。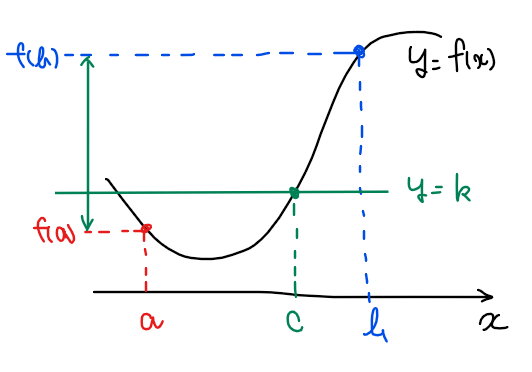

中間値の定理で述べられている『$\small f(a)$と$\small f(b)$の間の任意の値 $\small k$』というのは、『$\small f(a)$と$\small f(b)$の間に直線 $\small y=k$を引く』ということを意味しています。そして、『$\small f(c)=k$ $\small (a<c<b)$を満たす実数$\small c$が存在する』の部分は『関数$\small f(x)$と直線 $\small y=k$の交点の座標 $\small x=c$が $\small a<c<b$の範囲に存在する』ことを意味しています。このことは、上図から見ても確かに成り立つことが分かるでしょう。

以上の2点を踏まえると中間値の定理は次のように言い換えることができます。

Point：中間値の定理（翻訳版）

関数$\small f(x)$が$\small a ≦ x ≦b$の区間で繋がっている関数ならば、$\small f(a)$と$\small f(b)$の間にある直線と関数 $\small f(x)$は$\small a < x < b$の範囲に必ず交点を持つ

このように、$\small f(a)$と$\small f(b)$の中間の値に関する定理なので『中間値の定理』という名前がついています。

【講義2】頻出！中間値の定理の使い方

中間値の定理がどんな定理か理解できたところで、ここからは実際の問題でどのように利用するのかについて確認していきましょう。実は、中間値の定理は圧倒的によくでる使い方が決まっています。それが、『ある区間で方程式が実数解を持つことを示す問題』と『ある区間で2つの関数が交点を持つことを示す問題』です。方程式の実数解と関数の交点は本質的には同じ問題なので実質1パターンと考えることができます。

ではどのように中間値の定理を使うことができるのか、ここでは考え方のエッセンスだけ解説します。詳細は実際の問題と合わせて確認していきましょう。

方程式の実数解の例で解説すると、方程式 $\small f(x)=0$の解は関数 $\small y=f(x)$と$\small x$軸（定数関数 $\small y=0$）との交点と考えることができるので、$\small x$軸を挟むような 2点の$\small y$座標 $\small f(a)$、$\small f(b)$を見つけることで中間値の定理から『$\small f(a)$、$\small f(b)$の間にある $\small x$軸と$\small f(x)$は必ず交点を持つ』⇔『$\small f(x)=0$を満たす実数解が存在する』ことを示すことができます。

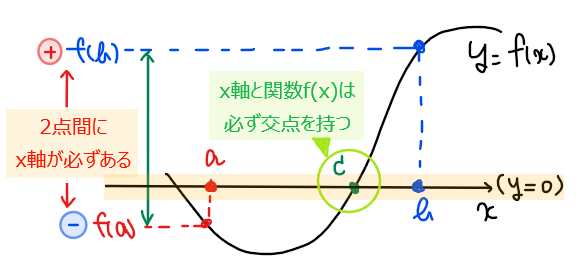
でも、$\small x$軸を挟むような2点の$\small y$座標 $\small f(a)$、$\small f(b)$なんてどう見つけるの？と疑問に思った人もいるかもしれませんが、$\small x$軸を挟んだ点であるということは、 $\small f(a)$と$\small f(b)$の片方がマイナス（$\small x$軸より下側）で片方がプラス（$\small x$軸より上側）になるので、必ず異符号になるということです。

よって、$\small f(a), \space f(b)$が異符号になることを示すことで、中間値の定理から関数 $\small f(x)$は$\small x$軸と少なくとも1箇所で交わることが示せます。

Point：中間値の定理（頻出形）

関数$\small f(x)$が連続関数かつ、閉区間$\small [a,b]$の端点において$\small f(a)$と$\small f(b)$が異符号であれば、関数$\small f(x)$は開区間$\small (a,b)$において少なくとも1つの実数解（$\small x$軸との交点）を持つ。

これは中間値の定理を$\small k=0$の場合としてただ言い換えただけですが、非常にあるあるな使い方なので絶対に覚えておきましょう！

【問題＆解説】中間値の定理を利用した問題

【問題1】中間値の定理の基本問題（難易度：★☆☆）

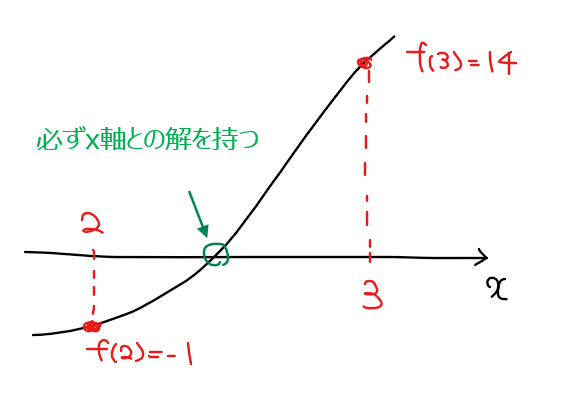
関数 $\small f(x)=x^3-4x-1$は $\small 2 < x < 3$の区間に$\small x$軸と少なくとも1つの交点を持つことを示せ。

問題解決のKey

・題意を示すためには、$\small f(c)=0$を満たす実数$\small c$が $\small 2<x<3$の区間に少なくとも1つ存在することを示せばよい。
・講義2の「中間値の定理（頻出形）」の考え方から、関数が連続であることと区間の端点で$\small y$座標の値が異符号であることを示せればよい。

【考察】
3次関数と$\small x$軸との交点の座標は、$\small x^3-4x-1=0$の3次方程式を解くことで求めることができる。一般に有理数解の候補は、
$$\small \displaystyle（有理数解の候補）=\pm \frac{（定数項の約数）}{（最高次数の約数）}$$
であり、本問の場合 $\small x= \pm1$が有理数解の候補となるがいずれも方程式の解にはなっていないことから、3次方程式の具体的な解を求めることは困難である。

　解説

関数 $\small f(x)$は3次関数なのですべての実数 $\small x$において連続 [*1]である。

*1：【補足】関数の連続性について
中間値の定理の記載に寄せて書くのであれば「閉区間$\small [2,3]$において連続なので…」という記載になりますが、本問では閉区間に限定しなくても実数全体で連続な関数となっています。全区間で連続な関数であれば、当然着目している閉区間でも連続になるので中間値の定理が適用できます。そのため、論証としては単に「すべての実数において連続」という点だけ触れていればOKです。
逆に、一部区間で連続ではない関数に対して中間値の定理を使いたい場合は、着目している区間内で連続ということを明言する必要があります。

また、閉区間 $\small 2≦ x ≦3$の端点の$\small y$座標は

\begin{split}
&\small f(2)=2^3-4\cdot 2-1=-1 \color{blue}{<0}\\
&\small f(3)=3^3-4\cdot 3-1=14 \color{red}{>0}\\
\end{split}

のように互いに異符号になっていることから、中間値の定理より関数 $\small f(x)$は $\small 2<x<3$の範囲において少なくとも1箇所で $\small x$軸と交点を持つ [*2]　（証明終）。

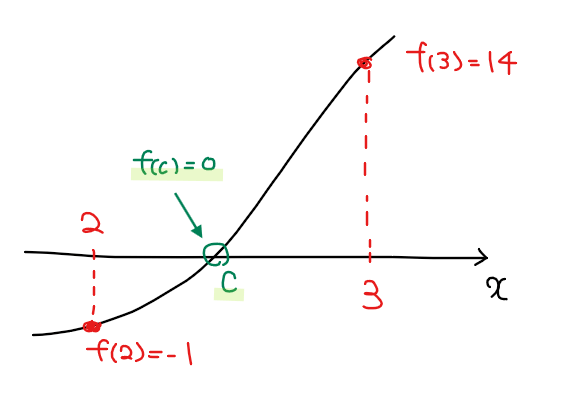
*2：【補足】中間値の定理との紐づけ
中間値の定理っぽく言えば、『$\small f(c)=0$を満たす実数$\small c$が $\small 2 <c < 3$の範囲に少なくとも1つ存在する』となります。

【問題2】方程式の実数解の存在証明（難易度：★☆☆）

方程式 $\small x-\cos x = 1$は $\small \displaystyle 0 < x < \frac{\pi}{2}$の範囲に少なくとも1つの実数解を持つことを示せ。

問題解決のKey

・方程式の実数解がある区間内に存在することの証明では、方程式のすべての文字・数字を左辺に移項し『文字・数字$\small =0$』の形に式変形した左辺を関数と見なすことで、問題1と同様に関数と $\small x$軸との交点が存在することを示す問題に帰着できる（下記のPoint参照）。

Point：『方程式の解』と『関数の交点』

・方程式の実数解の存在証明は以下の2つが同値であることから関数の交点の問題に置き換えて解くことができる。
　・方程式 $\small f(x)=g(x)$が実数解を持つ。
　・関数 $\small h(x)=f(x)-g(x)$が$\small x$軸と交点を持つ。

　解説

問題の方程式を

\begin{split}
&\small x-\cos x=1\\
\small \Leftrightarrow \space &\small x-\cos x-1=0\\
\end{split}

と式変形し、左辺を$\small f(x) = x-\cos x-1$をおくと、本問で求めたい『方程式 $\small x-\cos x =1$が$\small \displaystyle 0 < x < \frac{\pi}{2}$の範囲に実数解を持つこと』は、『関数 $\small f(x)$が$\small \displaystyle 0 < x < \frac{\pi}{2}$の範囲で$\small x$軸との交点を持つこと』を考えるのと同値である。

関数 $\small f(x)$はすべての実数に対して連続 [*1]であり、

*1：【補足】加減算された関数の連続性
関数 $\small y=x$、$\small y=\cos x$はそれぞれ連続関数なので、その和や差をとった関数も連続関数となる。

\begin{split}
\small f(0) &\small =0 -\cos 0 -1\\
&\small =-2\\
\small ∴ \space &\small \color{blue}{f(0)<0}\\
\end{split}

\begin{split}
\small f(\frac{\pi}{2}) &\small =\frac{\pi}{2} -\cos \frac{\pi}{2} -1\\
&\small =\frac{\pi}{2}-1\\
\small ∴ \space &\small \color{red}{f(\frac{\pi}{2})>0}\\
\end{split}

より、中間値の定理から関数 $\small f(x)$は $\small \displaystyle 0 < x < \frac{\pi}{2}$の範囲において少なくとも1箇所は$\small x$軸との交点を持つ。

よって、方程式 $\small x-\cos x =1$が$\small \displaystyle 0 < x < \frac{\pi}{2}$の範囲に少なくとも1つの実数解を持つことが示された（証明終）。

【問題3】大小関係を利用した解の存在証明（難易度：★★☆）

関数 $\small f(x)$と$\small g(x)$は$\small a≦x≦b$の範囲で連続な関数であり、$\small f(a) > g(a)$、$\small f(b) > g(b)$かつ、$\small a≦x≦b$の範囲における$\small f(x)$の最小値は$\small g(x)$の最小値より小さい。このとき、方程式 $\small f(x)=g(x)$は$\small a≦x≦b$の範囲において少なくとも2つの実数解を持つことを示せ。

問題解決のKey

問題文の条件が文字だけでは分かりにくいので、条件を満たす図をかいてみるとイメージが湧きやすいだろう。

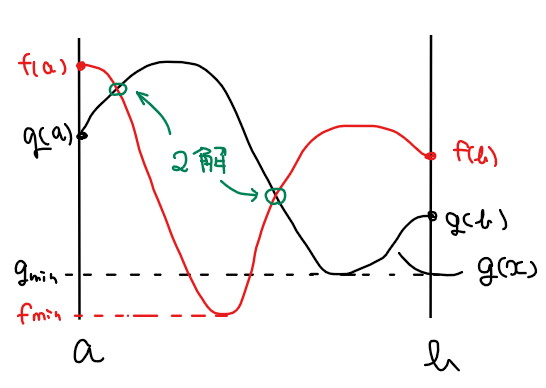
上図のように区間 $\small a≦x≦b$の端点で $\small f(x)$の方が大きく、最小値は$\small f(x)$の方が小さくなる必要があるので、少なくとも2箇所で2関数が交わる、すなわち方程式の解を少なくとも2つ持ちそうだということが分かるので、あとは『$\small x=a$ ～ $\small f(x)$の最小値』と『$\small f(x)$の最小値～ $\small x=b$』の各区間で中間値の定理を利用することで解の存在を証明すればよい。

　解説

$\small h(x)=f(x)-g(x)$とおく。

関数 $\small f(x), \space g(x)$が閉区間$\small [a,b]$で連続であることから、関数 $\small h(x)$も閉区間$\small [a,b]$で連続である。

また、関数 $\small f(x)$が最小値となるときの $\small x$座標を $\small x=c$（$\small a< c <b$）、関数 $\small g(x)$が最小値となるときの $\small x$座標を $\small x=d$（$\small a≦ d ≦b$）とおくと題意より$\small f(c)<g(d)$…① が成り立つ。

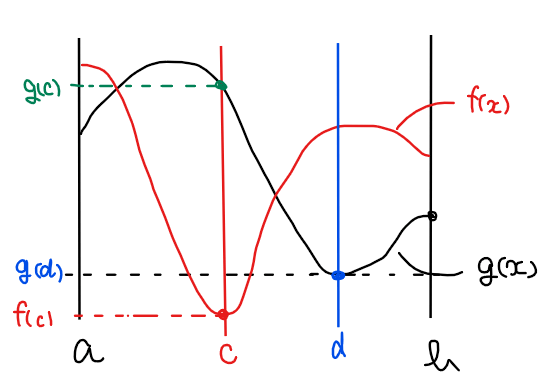
ここで、関数 $\small g(d)$は最小値なので、$\small g(d)≦g(c)$…② [*2]が成り立つことから

*2：補足
文字ばかりだと分かりにくいが、単純に$\small x=d$で関数$\small g(x)$が最小値ということは、$\small x \neq d$での関数$\small g(x)$の値は最小値以上の値になるということ。

①，②より、

\begin{split}
&\small f(c)<g(d) ≦ g(c)\\
\small ∴ \space &\small \color{#ef5350}{f(c)< g(c) \space \cdots ③}\\
\end{split}

よって、

\begin{split}
&\small h(a) = f(a)-g(a)>0 \space \cdots ④ \quad ( ∵ f(a)>g(a) )\\
&\small h(b) = f(b)-g(b)>0 \space \cdots ⑤ \quad ( ∵ f(b)>g(b) )\\
&\small h(c) = f(c)-g(c)<0 \space \cdots ⑥ \quad ( ∵ ③)\\
\end{split}

が成り立つ。

$\small a<c<b$であることに注意すると、関数$\small h(x)$は閉区間$\small [a,c]$で連続かつ $\small h(a)>0$, $\small h(c)<0$であることから、$\small a<x<c$の範囲で少なくとも1つの実数解を持つ。同様に、$\small h(x)$は閉区間$\small [c,b]$で連続かつ $\small h(c)<0$, $\small h(b)>0$であることから、$\small c<x<b$の範囲で少なくとも1つの実数解を持つ。

よって、関数$\small h(x)$、すなわち方程式$\small f(x)=g(x)$は$\small a<x<b$の範囲で少なくとも2つの実数解を持つ（証明終）。

【問題4】ただ一つの実数解を持つ証明（難易度：★★☆）

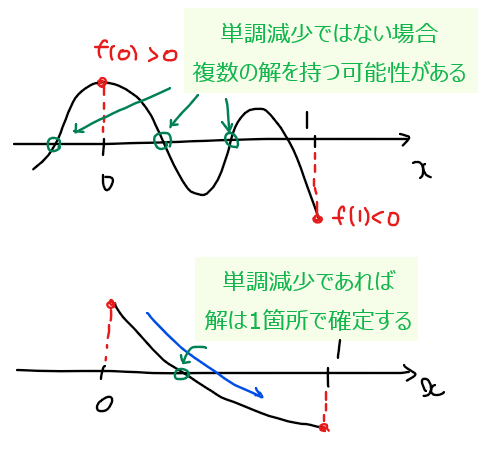
方程式 $\small x = e^{-2x+1}$はただ一つの解を持つことを示せ。 [日本大類]

問題解決のKey

・問題2同様に方程式の実数解の存在を示す問題だが、少し異なる点は区間の指定がないことと解の個数がただ一つに限定されている点である（問題2では『少なくとも1つ』だったので2つ以上解が存在してもよかった）。
・方程式を『文字・数字=0』の形にした後は、区間指定がないので$\small x=0,\pm 1, \cdots$と適当な値を試すことで関数$\small f(x)$の符号が変わる区間を地道に探す。
・ただ一つの解の存在（$\small x$軸との交点が1箇所のみ）を証明するためには、関数が単調増加あるいは単調減少であることを示せばよい。

　解説

問題の方程式を

\begin{split}
&\small x= e^{-2x+1}\\
\small \Leftrightarrow \space &\small e^{-2x+1}-x=0\\
\end{split}

と変形し、$\small f(x)=e^{-2x+1}-x$とおく。

\begin{split}
\small \color{#ef5350}{ f(0)} &\small \color{#ef5350}{= e >0 \space \cdots ①}\\
\end{split}

\begin{split}
\small f(1) &\small = e^{-2+1}-1\\
&\small = \frac{1}{e}-1\\
\end{split}

より、$\small e > 1$なので、$\small f(1) < 0 \space \cdots ②$.

関数 $\small f(x)$はすべての実数に対して連続であることと①、②の結果より、中間値の定理から関数 $\small f(x)$は$\small 0<x<1$の範囲に少なくとも1つの実数解を持つ。よって、方程式 $\small x =e^{-2x+1}$は$\small 0<x<1$の範囲に少なくとも1つの実数解を持つ。

あとは、$\small f(x)$が $\small f(0)>0$、$\small f(1)<0$であることから、関数$\small f(x)$が単調減少であることが示せれば $\small 0<x<1$の範囲に1つだけ実数解を持つこと、および他の区間では実数解を持たないことが示せることから、すべての実数に対してただ一つの実数解を持つことが示せる。

関数$\small f(x)$の微分から増減を確認すると

\begin{split}
\small f^\prime(x) &\small = -2e^{-2x+1}-1\\
&\small = -(2e^{-2x+1}+1)\\
\end{split}

ここで、すべての実数 $\small x$に対して $\small 2e^{-2x+1}+1 >0$が成り立つ [*1]ことから

*1：補足
自然対数の底 $\small e$は正の数なので何乗しても正の数になる。指数が負の数になる場合でも、$\small \displaystyle e^{-2}=\frac{1}{e^2}$のように逆数になるだけなので負の数にはならないことに注意。

\begin{split}
&\small -(2e^{-2x+1}+1) <0\\
&\small \quad ∴ \space f^\prime(x) < 0\\
\end{split}

となるため、関数 $\small f(x)$はすべての区間で単調減少関数（$\small x$の値が増えるにつれて$\small y$の値が減少していく関数）である。

よって、単調減少関数 $\small f(x)$が $\small f(0)>0$、$\small f(1)<0$となることから、$\small 0<x<1$の区間でただ一つの実数解を持つため、方程式 $\small x=e^{-2x+1}$はただ一つの実数解を持つことが示せた（証明終）。

本記事のまとめ

今回は中間値の定理の意味と典型問題の解法について解説しました。イメージさえ一度理解できれば、主張自体は意外とシンプルな定理でした。また、実際の問題では関数と$\small x$軸の交点の存在証明で利用されることが多い定理ということも問題を通して実感できたかと思います。方程式の実数解の存在証明の問題も関数と$\small x$軸との交点の問題に置き換えて解く考え方は頻出なのでしっかりとマスターしておきましょう。

では、最後に本記事のポイントを復習して終わりにしましょう！

☆重要ポイント☆
≪中間値の定理とは？≫
・関数$\small f(x)$が$\small a ≦ x ≦b$の区間で繋がっている関数ならば、$\small f(a)$と$\small f(b)$の間にある直線と関数$\small f(x)$は$\small a < x < b$の範囲に必ず交点を持つ。

≪中間値の定理の頻出形≫
関数$\small f(x)$が連続関数かつ、閉区間$\small [a,b]$の端点において$\small f(a)$と$\small f(b)$が異符号であれば、関数$\small f(x)$は開区間$\small (a,b)$において少なくとも1つの実数解（$\small x$軸との交点）を持つ。

≪よく使う問題の置き換え≫
・方程式の実数解の存在証明は以下の2つが同値であることから関数の交点の問題に置き換えて解くことができる。
　・方程式 $\small f(x)=g(x)$が実数解を持つ。
　・関数 $\small h(x)=f(x)-g(x)$が$\small x$軸と交点を持つ。