今回は複素平面上での複素数の回転や拡大について解説してこうと思います。複素数のかけ算や割り算が図形的には回転や拡大に対応すると言われても今一つピンと来ないだよな…、と思っている人は意外と多いと思います。
そこで本記事では、複素数の積・商の計算がなんで複素数平面上での回転や拡大であると解釈できるのか、複素数の計算と図形的な意味合いの対応関係について分かりやすく解説していこうと思います。また複素数の表し方の一種である極形式についても回転や拡大と非常に大きな関係があるので一緒に解説していこうと思います。
複素平面の分野の中でも非常に重要な内容になっているので、是非最後まで一緒に確認していきましょう!
- 複素数の積や商が複素数平面上の回転や拡大になる理由について理解したい人
- 複素数の回転・拡大に関する問題の解き方のコツを知りたい人
- 定期テスト対策、受験対策がしたい人
【基礎講義】複素数の回転と拡大
【講義1】基本用語の説明(複素数、複素数平面、極形式)
複素数の回転や拡大の解説に入る前にまずは基本用語の意味から復習しておこうと思います。
なぜここであえて用語の復習から始めるかというと、複素数の分野は新しい概念が多いので用語の意味をイメージまで含めてしっかり理解しておくことで解説をすんなり理解することにつながるからです。
用語の意味はばっちりだ!という人は『【講義2】複素数の積・商の図形的意味(回転・拡大)』から確認をはじめましょう!
≫ 複素数とは?
・実数(\(\small 1,-2,\sqrt{2} \cdots \space etc.\))と虚数(\(\small i,-2i \cdots \space etc.\) )を組み合わせた数のこと。
例:\(\small \displaystyle 2-i,\quad -1+3i, \quad \frac{1}{2}+\frac{\sqrt{3}}{2}i \cdots \space etc.\)
・複素数の実数部分を実部と言う。
例:\(\small 1-3i\)の実部は\(\small 1\)
・複素数の虚数部分を虚部と言う。
例:\(\small 1-3i\)の虚部は\(\small -3\)
【補足】複素数と実数・虚数の関係性
実数は虚部が0、虚数は実部が0という複素数の特別な場合と考えれば、実数も虚数も広い意味では複素数となります。
このように数学で新しい概念が登場するときは、これまでとはまったく異なる新しいものとして捉えるのではなく、これまでの概念の拡張版と捉えることが重要だったりします。
≫ 複素数平面とは?
・複素数を表すための平面(数直線の複素数版!)。
・横軸に実部、縦軸に虚部の値をプロットすることで表される1つの点が1つの複素数を表す。
・横軸を実軸、縦軸を虚軸と呼ぶ。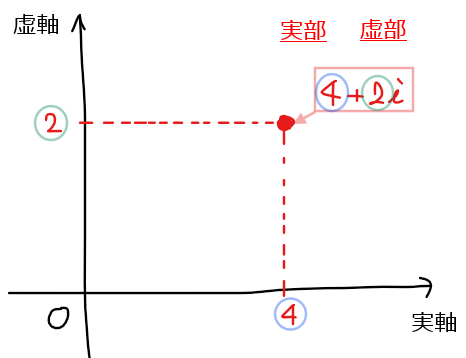
【注意点】\(\small xy\)平面と複素数平面の違い
実数を表すためには数直線を使ってきましたが、複素数は数直線上に表すことができません。そこで実軸(=数直線)に虚軸を足した平面上で一つの点を表すという発想が生まれました。
一見すると\(\small xy\)平面と複素数平面は同じに見えますが、\(\small xy\)平面は\(\small x\)と\(\small y\)という2つの値の関係性を表すための平面であるのに対して複素数平面はあくまで1つの複素数を表すための平面という点が大きな違いなので注意しましょう。
≫ 極形式とは?
・複素数を『原点からの距離』と『角度』を使って表すこと。
・複素数\(\small z\)の原点からの距離は、\(\small |z|\)と表す。
・複素数\(\small z\)の角度を偏角と言い、\(\small \arg z\)と表す。
・原点からの距離を\(\small r\)、偏角を\(\small \theta\)とする複素数\(\small z\)を極形式で表すと
$$\small \color{#ef5350}{z = r(\cos \theta +i\sin \theta)}$$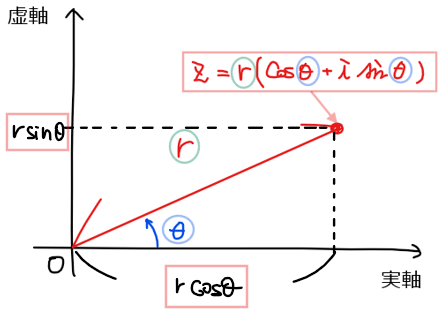
複素数を複素数平面上で表すときに、普通は実部と虚部の値で表すのが一般的でしょう。たとえば、実部が\(\small 2\)で虚部が\(\small -1\)の複素数は\(\small 2-i\)という具合です。でも、複素数は絶対に実部と虚部で表さないといけないというルールはありません。実部と虚部を用いて1つの複素数を表す以外の方法としてよく使われるのが原点からの距離と角度で表す方法です。
例:原点からの距離が\(\small \sqrt{2}\)、偏角が\(\small \displaystyle \frac{\pi}{4}\)の複素数
⇒極形式で表すと、\(\small \displaystyle \sqrt{2}\left(\cos \frac{\pi}{4}+i \sin \frac{\pi}{4}\right)\)になります。
※極形式の詳細については解説すると長くなるので詳しくは「【数C_複素数平面】複素数を極形式へ変換する方法(公式不要の裏ワザ的解法)」を見てね!
【講義2】複素数の積・商の図形的意味(回転・拡大)
本記事の最重要ポイントである複素数のかけ算、割り算の図形的な意味について解説します。
実数の世界に例えるなら、2つの実数 \(\small 2,5\)を足し算すると数式的な計算結果は\(\small 7\)ですが、図形的には数直線で2から右方向に5だけ移動するという意味を持っています。
これと同じような考察を複素数の積・商について考えていたいというのがこの章の目的です。複素数の積や商という数式上の計算と、複素平面上での意味、すなわち図形的な意味を考えていきましょう。
では、なぜ複素数の積・商が図形的に回転や拡大を表すのかについて、実際の計算を通して解説していきます。図形的な意味を理解するうえでは、原点との距離や回転角が分かりやすいように複素数を極形式で表しておくと計算前後の比較がしやすく便利です。
複素数 \(\small z = a(\cos \alpha + i \sin \alpha)\)と複素数 \(\small w = b(\cos \beta + i \sin \beta)\)の積 \(\small zw\)の数式的な計算と図形的な意味合いについて解説します。
複素数の積の数式的な計算
\begin{split}
\small zw &\small = \{a(\cos \alpha + i \sin \alpha)\}\{b(\cos \beta + i \sin \beta)\}\\
&\small = ab(\cos \alpha + i \sin \alpha)(\cos \beta + i \sin \beta)\\
&\small = ab(\cos \alpha \cos \beta +i\cos \alpha \sin \beta \\
&\small \qquad + i \sin \alpha \cos \beta +i^2\sin \alpha \sin \beta)\\
&\small = ab\{\cos \alpha \cos \beta -\sin \alpha \sin \beta\\
&\small \qquad + i (\sin \alpha \cos \beta +\cos \alpha \sin \beta)\}\\
&\small = ab(\cos (\alpha+\beta)+i\sin(\alpha+\beta)) \quad \cdots ①\\
\end{split}
※補足
最後の式変形は、三角関数の加法定理を利用している。
\begin{split}
&\small \cos \alpha \cos \beta -\sin \alpha \sin \beta=\cos(\alpha + \beta)\\
&\small \sin \alpha \cos \beta +\cos \alpha \sin \beta =\sin(\alpha+\beta)\\
\end{split}
①の計算結果から、かけ算後の複素数は、原点からの距離が\(\small ab\)、偏角が\(\small \alpha+\beta\)の複素数であることが分かります。
ここから複素数の積の図形的な意味を確認していきましょう。
複素数の積の図形的な意味合い
\(\small b(\cos \beta +i\sin \beta)\)を掛け算すると…
・原点からの距離:\(\small b\)倍
・回転角:偏角\(\small \beta\)だけ反時計回りに回転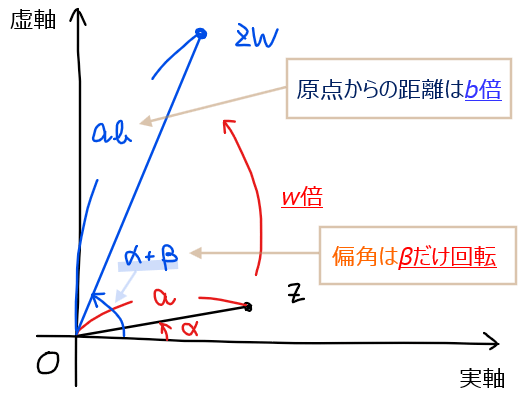
原点からの距離は2つの複素数の原点から距離の積になっており、もともと複素数の距離が\(\small a\)だったものが、複素数\(\small w \)をかけ算することで\(\small ab\)になる(かけ算した複素数\(\small w\)の原点からの距離倍 になる)。
偏角は2つの複素数の和になっており、もともと複素数の偏角が\(\small \alpha\)だったものが、複素数\(\small w \)をかけ算することで\(\small \alpha+\beta\)になる(かけ算した複素数\(\small w \)の偏角\(\small \beta \)分だけ反時計回りに回転する)。
複素数の商についても同様に数式的な計算と図形的な意味合いを確認していきましょう。
複素数の商の数式的な計算
\begin{split}
\small \displaystyle \frac{z}{w} &\small =\frac{a(\cos \alpha + i \sin \alpha)}{b(\cos \beta + i \sin \beta)}\\
&\small =\frac{a(\cos \alpha + i \sin \alpha)\color{#ef5350}{(\cos \beta – i \sin \beta)}}{b(\cos \beta + i \sin \beta)\color{#ef5350}{(\cos \beta – i \sin \beta)}}\\
&\small =\frac{a(\cos \alpha + i \sin \alpha)(\cos \beta – i \sin \beta)}{b(\cos^2 \beta +\sin^2 \beta)}\\
&\small \displaystyle = \frac{a}{b}(\cos (\alpha-\beta)+i\sin(\alpha-\beta)) \quad \cdots ②\\
\end{split}
②の計算結果から、割り算後の複素数は、原点からの距離が\(\small \displaystyle \frac{a}{b}\)、偏角が\(\small \alpha-\beta\)の複素数であることが分かります。
ここから複素数の商の図形的な意味を確認していきましょう。
複素数の商の図形的な意味合い
\(\small b(\cos \beta +i\sin \beta)\)で割り算すると…
・原点からの距離:\(\small \displaystyle \frac{1}{b}\)倍
・回転角:偏角\(\small \beta\)だけ時計回りに回転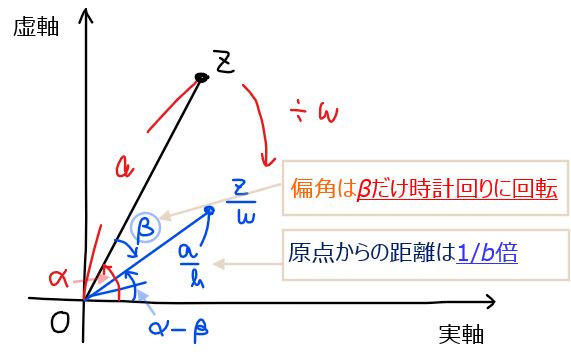
原点からの距離は2つの複素数の原点からの距離の商になっており、もともと複素数の距離が\(\small a\)だったものが、複素数\(\small w \)で割り算することで\(\small \displaystyle \frac{a}{b}\)になる(割り算した複素数\(\small w \)の『原点からの距離』の逆数倍になる)。
偏角は2つの複素数の差になっており、もともと複素数の偏角が\(\small \alpha\)だったものが、複素数\(\small w \)で割り算することで\(\small \alpha-\beta\)になる(割り算した複素数\(\small w \)の偏角\(\small \beta \)分だけ時計回りに回転する)。
ここまでは、『複素数の積・商』から『複素数の原点からの距離や回転角』がどう変化するかを解説してきました。では、最後は逆に『原点からの距離や回転角の変化(指定した分だけ移動)』させたい場合に『どんな複素数を掛け算(または割り算)』すればよいかについて確認していきましょう。
さっきまでは\(\small b(\cos \beta + i\sin \beta)\)を掛け算すると、原点からの距離が\(\small b\)倍、原点を中心に\(\small \beta\)回転すると言っていたのを逆に考えて、原点からの距離を\(\small b\)倍、原点を中心に\(\small \beta\)回転させたければ、\(\small b(\cos \beta + i\sin \beta)\)を掛け算すればよい、と主張しているだけですね(Pointと使っている文字が異なっていて分かりにくいですが、\(\small b=r\)、\(\small \beta=\theta\)とすると対応します)。
割り算の場合は、原点からの距離を\(\small \displaystyle \frac{1}{b}\)倍、原点を中心に\(\small -\beta\)回転(割り算の場合は時計回りに回転なのでマイナス符号つく)させたければ、\(\small b(\cos \beta+i\sin \beta)\)で割り算すると考えてももちろん正解なのですが、割り算は一般的に計算が面倒なので、\(\small \displaystyle \frac{1}{b}(\cos( -\beta)+i\sin( -\beta))\)を掛け算すると考えれば同じ移動を表現できます。これは、Pointに記載の\(\small \displaystyle r = \frac{1}{b}\)、\(\small \theta = -\beta\)の場合に相当するので、結局、複素数のかけ算だけで複素数の移動を表現できるわけです。
このポイントは暗記必須です!個人的には、数学で暗記はおすすめしていないのですが、今回は導出が大変&頻出の知識なので、覚えちゃった方が得策です!
【問題&解説】複素数の回転・拡大に関する問題
【基本問題】回転・拡大した複素数を求める問題
(1)複素数\(\small z=3-2i \)を原点を中心に\(\small \displaystyle \frac{\pi}{3}\)だけ回転した点を表す複素数を求めよ。
(2)複素数\(\small z=3-2i \)の原点からの距離を\(\small \displaystyle \frac{2}{3}\)倍にした点を表す複素数を求めよ。
(3)複素数\(\small z=1+i \)の原点からの距離を\(\small \displaystyle 2\)倍、原点を中心に時計回りに\(\small \displaystyle \frac{\pi}{4}\)だけ回転した点を表す複素数を求めよ。
詳細は、【講義2】複素数の積・商の図形的意味(回転・拡大)参照。
≫ 複素数の回転・拡大
原点からの距離を\(\small r\)倍、原点を中心に\(\small \theta\)回転した複素数を求めたければ複素数に \(\small \displaystyle r(\cos\theta + i\sin \theta)\)を掛け算すればよい!
≫ 複素数の回転
点\(\small z\)を原点を中心に\(\small \theta\)回転した複素数は \(\small \displaystyle z(\cos\theta + i\sin \theta)\)
※原点からの距離は変わらないので\(\small r=1\)
≫ 複素数の拡大
点\(\small z\)の原点からの距離を\(\small r\)倍した複素数は \(\small \displaystyle rz\)
※回転しないので\(\small \theta=0\)
複素数を\(\small r\)倍に拡大し\(\small \theta\)回転させたい場合は、原点からの距離\(\small r\)、偏角が\(\small \theta\)の複素数である\(\small r(\cos \theta +i\sin \theta)\)を掛け算すればよい。
本問の場合は、原点からの距離は変えないので\(\small r=1\)、回転角は\(\small \displaystyle \theta = \frac{\pi}{3}\)であることから、
\begin{split}
&\small \displaystyle \cos \frac{\pi}{3}+i\sin \frac{\pi}{3}\\
&\small \displaystyle =\frac{1}{2}+\frac{\sqrt{3}}{2}i\\
\end{split}
これを\(\small z=3-2i\)にかけ算すれば\(\small \displaystyle \frac{\pi}{3}\)だけ回転した複素数が求まるので、
\begin{split}
&\small \displaystyle (3-2i)\left(\frac{1}{2}+\frac{\sqrt{3}}{2}i\right)\\
&\small \displaystyle =\frac{3}{2}+\sqrt{3}+\left(\frac{3\sqrt{3}}{2}-1\right)i\\
&\small \displaystyle =\color{red}{\frac{3+2\sqrt{3}}{2}+\frac{3\sqrt{3}-2}{2}i \space \cdots 【答】}\\
\end{split}
原点からの距離を\(\small \displaystyle \frac{2}{3}\)倍、回転はなしであることから、\(\small \displaystyle r=\frac{2}{3}, \space \theta=0\)の複素数、すなわち、
\begin{split}
&\small \displaystyle \frac{2}{3}(\cos 0 + i\sin 0)\\
&\small \displaystyle =\frac{2}{3}(1 + i\cdot 0)\\
&\small \displaystyle =\frac{2}{3}\\
\end{split}
を複素数\(\small z=3-2i\)にかけ算すればよいので
\begin{split}
&\small \displaystyle \frac{2}{3}(3-2i)\\
&\small \displaystyle =\color{red}{2-\frac{4}{3}i \space \cdots 【答】}\\
\end{split}
原点からの距離を\(\small 2\)倍、時計回りに\(\small \displaystyle \frac{\pi}{4}\)回転したいので、原点からの距離が\(\small 2\)、偏角が\(\small \displaystyle -\frac{\pi}{4}\) [*1]の複素数を\(\small z = 1 + i\)に掛け算してあげれば求めることができる。
*1:【補足】時計回りの回転
回転方向は通常、反時計回りが正、時計回りが負であることに注意すると、今回は時計回りに\(\small \displaystyle \frac{\pi}{4}\)回転なのでマイナスの符号をつける必要がある。
あるいは、複素数の割り算が時計回りの回転の意味をもつことから、原点からの距離1、偏角\(\small \displaystyle \frac{\pi}{4}\)の複素数で割り算してもよい(別解参照)。
よって、
\begin{split}
&\small \displaystyle (1+i)\cdot \color{#ef5350}{2\left\{\cos \left(-\frac{\pi}{4}\right)+i\sin \left(-\frac{\pi}{4}\right)\right\}}\\
&\small \displaystyle =2 (1+i)\left(\frac{1}{\sqrt{2}}-\frac{1}{\sqrt{2}}i\right)\\
&\small \displaystyle =\frac{2}{\sqrt{2}}(1+i)(1-i)\\
&\small \displaystyle =\sqrt{2}\cdot 2\\
&\small \displaystyle =\color{red}{2\sqrt{2} \space \cdots 【答】}\\
\end{split}
【別解】商を用いた求め方
複素数の割り算には複素数を時計回りに回転させるという図形的意味合いがあったことを思い出すと、原点からの距離を2倍した後に、偏角が\(\small \displaystyle \frac{\pi}{4}\)、原点からの距離が1(長さを変えない)の複素数で割り算を行っても所望の複素数を求めることができる。
まず、原点からの距離を2倍した複素数は単純に2倍すればよいので、\(\small 2z = 2+2i\)。次に、原点からの距離が1で偏角が\(\small \displaystyle \frac{\pi}{4}\)の複素数は、
\begin{split}
&\small \displaystyle \cos \left(\frac{\pi}{4}\right)+i\sin \left(\frac{\pi}{4}\right)\\
&\small \displaystyle =\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}}i\\
&\small \displaystyle =\frac{1}{\sqrt{2}}(1+i)\\
\end{split}
であることから、\(\small 2+2i\)をこの複素数で割り算することで
\begin{split}
&\small \displaystyle \frac{2+2i}{\frac{1}{\sqrt{2}}(1+i)}\\
&\small \displaystyle =\frac{2(1+i)}{\frac{1}{\sqrt{2}}(1+i)}\\
&\small \displaystyle =2\sqrt{2}\cdot \frac{1+i}{1+i}\\
&\small \displaystyle =2\sqrt{2}\\
\end{split}
のように求めることができる。
ただ、一般的に複素数の割り算は分数計算が複雑になることから、複素数の積として考えるのがおすすめである。
【標準問題】複素数の回転角、原点の距離を求める問題
2つの複素数\(\small z=\sqrt{3}+i, \space w \)について、点\(\small \displaystyle \frac{w}{z}\)は点\(\small w\)をどのように移動した点か。
複素数\(\small z=r(\cos \theta +i\sin \theta)\)で割り算する場合の図形的意味は…
・原点からの距離:\(\small \displaystyle \frac{1}{r}\)倍
・回転角:\(\small \theta\)だけ時計回りに回転
複素数がどのように移動するかといった図形的意味を把握するためには、元となる複素数 \(\small w\)に対して、割り算している\(\small z\)を極形式で表し、原点からの距離と回転角が確認できればよい。
よって、\(\small z\)を極形式で表すと
\begin{split}
&\small \displaystyle \sqrt{3}+i\\
&\small \displaystyle =2\left(\frac{\sqrt{3}}{2}+\frac{1}{2}i\right) \space [*1]\\
&\small \displaystyle =2\left(\cos \frac{\pi}{6}+i\sin \frac{\pi}{6}\right)\\
\end{split}
と式変形できるので、複素数\(\small z\)は原点からの距離が2、偏角が\(\small \displaystyle \frac{\pi}{6}\)の複素数であることが分かった。
*1:【補足】極形式への変換
実部と虚部が\(\small \sqrt{3}\)、1となっていることから、\(\small \displaystyle \frac{\sqrt{3}}{2}, \space \frac{1}{2}\)の形を作り出す方針で式変形する。
よって、複素数の商の図形的意味から、\(\small \displaystyle \frac{w}{z}\)は点\(\small w\)の原点からの距離を\(\small \displaystyle \frac{1}{2}\)倍(半分)し、原点まわりに時計回りに\(\small \displaystyle \frac{\pi}{6}\)だけ回転した点である …【答】.
【補足】
回転角は、原点まわりに\(\small \displaystyle -\frac{\pi}{6}\)だけ回転した点と解答してもOK
【応用問題】\(\small xy\)平面上の座標の回転
\(\small xy\)座標平面上の点\(\small \mathrm{P}(1,3)\)を原点を中心に反時計回りに\(\small \displaystyle \frac{\pi}{3}\)だけ回転した点\(\small \mathrm{Q}\)の座標を求めよ。
すなわち、
$$\small \color{#ef5350}{(x+iy)(\cos \theta +i \sin \theta)}$$
で求まる複素数の実部を\(\small x\)座標、虚部を\(\small y\)座標とした座標が回転後の座標となる。
【豆知識】:回転した座標を求める公式
\begin{split}
&\small (x+iy)(\cos \theta +i \sin \theta)\\
&\small =(x\cos\theta+i^2 y\sin\theta)+i(x\sin\theta +y\cos\theta)\\
&\small =(x\cos\theta- y\sin\theta)+i(x\sin\theta +y\cos\theta)\\
\end{split}
となることから、点\(\small (x,y)\)を原点を中心に\(\small \theta\)だけ回転させた座標は
$$\small (x\cos\theta- y\sin\theta, x\sin\theta +y\cos\theta)$$
で求まる。
\(\small xy\)座標平面上の点の回転は、複素数平面上の複素数の回転に対応させて考えると簡単である。
【補足】なんで急に複素数平面が登場するの?
問題自体は\(\small xy\)座標平面上の点の回転の話なのに、いきなり複素数が出てくることに疑問を感じた人もいるでしょう。
確かに、両者は全然別の概念ですが、複素数の位置と座標には非常に深い対応関係があります。具体的には、複素数平面の実部を\(\small x\)座標、虚部を\(\small y\)座標と見なせば、複素数平面上の1つの複素数の位置を\(\small xy\)平面上の1点と見なすことができます。
この対応関係を利用すれば、複素数の回転が\(\small xy\)平面上の点を回転したときの座標の計算に使えるぞ!という発想が出てくるのも自然です。
このように複素数といういわば実在しない数の計算が、\(\small xy\)平面上の座標の回転という実在する物事の計算に利用できるのは面白いですね。点の回転以外にも複素数の計算が活用できる例は実は色々あって、一見複雑で解けない積分の変数を複素数に置き換えて計算する複素積分や、私たちが日常的に使っている電力の計算(交流回路の計算)にも応用されています。数学って実に奥が深いですね。
点 \(\small \mathrm{P}(1,3)\)を\(\small \displaystyle \frac{\pi}{3}\)回転させた座標を求めることは、複素数平面上の複素数 \(\small z = 1+3i\)を\(\small \displaystyle \frac{\pi}{3}\)回転させた複素数を求めることに対応するので、
\begin{split}
&\small \displaystyle z\left(\cos \frac{\pi}{3} + i\sin \frac{\pi}{3} \right)\\
&\small \displaystyle =(1+3i)\left(\frac{1}{2} +\frac{\sqrt{3}}{2}i \right)\\
&\small \displaystyle =\frac{1-3\sqrt{3}}{2}+\frac{3+\sqrt{3}}{2}i\\
\end{split}
よって、求めた複素数の実部を\(\small x\)座標、虚部を\(\small y\)座標とする点が求めたい点\(\small \mathrm{Q}\)の座標になるので、\(\small \displaystyle \mathrm{Q}\left(\frac{1-3\sqrt{3}}{2},\frac{3+\sqrt{3}}{2}\right)\)…【答】.
【別解】
豆知識で紹介した公式を用いれば
\begin{split}
&\small (x\cos\theta- y\sin\theta, x\sin\theta +y\cos\theta)\\
&\small =\left(1\cdot \cos\frac{\pi}{3}- 3\cdot \sin\frac{\pi}{3}, 1\cdot \sin\frac{\pi}{3}+3\cdot \cos\frac{\pi}{3} \right)\\
&\small = \left(\frac{1}{2}-3\cdot \frac{\sqrt{3}}{2},\frac{\sqrt{3}}{2}+3\cdot \frac{1}{2}\right)\\
&\small =\color{red}{\left(\frac{1-3\sqrt{3}}{2},\frac{3+\sqrt{3}}{2}\right) \space \cdots 【答】}\\
\end{split}
と求めることができる。
本記事のまとめ
今回は複素数の積と商が回転、拡大・縮小という図形的な意味を持つ理由について徹底解説してみました。今回学んだ内容は複素数平面の分野の基礎になる部分なので、問題が解けるようになるまで考え方含めてしっかり理解しておきましょう。
また、複素数平面上の回転が\(\small xy\)平面上の座標の回転にも応用できるという考え方も非常によく出てくるので今回の問題を通して押さえておきましょう。
では最後に今回の重要ポイントを復習して終わりにしましょう。
☆重要ポイント☆
≫ 複素数の積・商の図形的意味
複素数平面上では原点を中心とした回転と原点との距離の拡大・縮小を意味する
≫ 複素数の回転・拡大(縮小)の方法
移動前の複素数を\(\small z\)として、原点との距離を\(\small r\)倍、原点まわりに\(\small \theta\)回転させた複素数は、\(\small z\)に\(\small r (\cos \theta+i\sin \theta )\)を掛け算することで求められる。
今回は以上です。お疲れさまでした!







コメント