今回はド・モアブルの定理とはどんな定理なのかについて解説していきます。また、ド・モアブルの定理を利用する典型問題についても紹介していきますが、範囲が広いため今回は複素数の累乗を計算する問題に焦点を絞って分かりやすく解説していこうと思います。
本記事を通してド・モアブルの定理の使い方をしっかりマスターしておきましょう。
- ド・モアブルの定理について知りたい人
- ド・モアブルの定理を利用した複素数の累乗の計算方法を知りたい人
- 定期テスト対策、受験対策がしたい人
【基礎講義】ド・モアブルの定理と典型問題
【講義1】ド・モアブルの定理とは
まずはじめにド・モアブルの定理がどんな定理なのか確認しておきましょう。
$$\small \color{#ef5350}{(\cos \theta +i\sin \theta)^n = \cos n\theta +i\sin n\theta}$$
が成り立つ。
ド・モアブルの定理のすごいところは、\(\small n\)乗の計算が偏角の\(\small n\)倍に置き換わっている点です。一般に\(\small n\)乗の計算より\(\small n\)倍の計算の方が楽(例えば\(\small 2^{100}\)は計算できないくらい大変ですが\(\small 2\)の\(\small 100\)倍はすぐ計算できますね)なので、非常に威力を発揮する公式になります。
≪ド・モアブルの定理の利用例≫
\(\small \displaystyle \left(\cos \frac{\pi}{3}+i\sin \frac{\pi}{3}\right)^{12}\)の計算は、ド・モアブルの定理を利用すると
\begin{split}
\small \left(\cos \frac{\pi}{3}+i\sin \frac{\pi}{3}\right)^\color{red}{12} &\small=\cos \left(\frac{\pi}{3} \times \color{red}{12}\right)+i\sin \left(\frac{\pi}{3} \times \color{red}{12}\right)\\
&\small=\cos 4\pi +i\sin 4\pi \\
&\small=1 +i\cdot 0\\
&\small=\color{red}{1\space \cdots 【答】}\\
\end{split}
のように簡単に計算できます。
また、一般に原点からの距離が\(\small r\)、偏角が\(\small \theta \)の複素数は極形式で\(\small r(\cos \theta +i\sin \theta)\)と表せることに着目すると、\(\small \cos \theta +i\sin \theta \)部分がド・モアブルの定理そのものなので、
\begin{split}
\small \{r(\cos \theta +i\sin \theta)\}^n &\small = r^n\color{#ef5350}{(\cos \theta +i\sin \theta)^n}\\
&\small = r^n\color{#ef5350}{(\cos n\theta +i\sin n\theta)}\\
\end{split}
と計算ができます。つまり、一般に複素数の累乗(\(\small n\)乗)は、原点からの距離を\(\small n\)乗し、偏角を\(\small n\)倍した複素数になることが分かります。
【講義2】ド・モアブルの定理の典型問題3選
この章ではド・モアブルの定理を利用した典型問題について解説していきます。
II. 実数\(\small p\)の\(\small n\)乗根の計算
III. 三角関数(\(\small \cos \theta \)、\(\small \sin \theta \))を含む等式証明
1つ目は前章のド・モアブルの定理の中でも触れましたが、複素数の\(\small n\)乗の計算で利用します。\(\small n\)乗の計算が原点からの距離の\(\small n\)乗と偏角の\(\small n\)倍になるという計算するうえで非常に重要となる定理なので、このあとの演習問題を通してしっかり使いこなせるレベルまで理解を深めてましょう。
2つ目はその逆で、\(\small n\)乗が計算できるということは\(\small n\)乗根(\(\small n\)乗する前の数)も求めることができます。特に、\(\small z^n\)を含む方程式を解く問題が頻出になります。
↓↓\(\small n\)乗根の問題はこちらの記事で解説↓↓
【数C_複素数平面】複素数のn乗根の求め方と図形的意味(ド・モアブルの定理の利用)
最後の3つ目が少し分かりにくいと思いますが、うまく選んだ複素数に対してド・モアブルの定理を適用し実部と虚部を係数比較することで、\(\small \sin \theta \)や\(\small \cos \theta\)を含む等式を証明する問題です。
証明の方針自体は決まっているのでそれほど難しくはないですが、どのような式を展開するかの設定が慣れないうちは難しいかもしれません。
また、問題を解くのとは別の使い道として、三角関数の諸公式を忘れてしまったときにド・モアブルの定理で導出することができます。これは豆知識として知っておくと便利です。
↓↓三角関数の等式証明(3倍角の公式の簡単な導出方法)はこちらで解説↓↓
【数C_複素数平面】ド・モアブルの定理を利用した3倍角の公式の導出(三角関数を含む等式証明)
【問題&解説】ド・モアブルの定理を用いた典型問題
【問題1】ド・モアブルの定理の基本問題(難易度:★☆☆)
次の式を計算せよ。
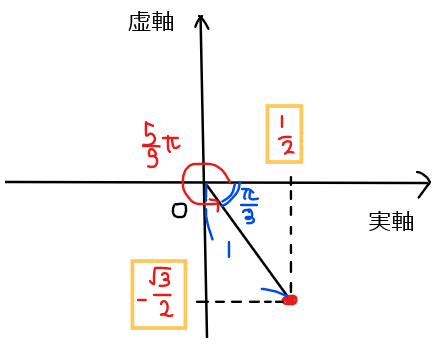
(1)\(\small \displaystyle \left(\cos \frac{\pi}{3}+i\sin \frac{\pi}{3}\right)^5\)
(2)\(\small \displaystyle \left(\cos \frac{\pi}{4}+i\sin \frac{\pi}{4}\right)^{-6}\)
まずはド・モアブルの定理の使い方から確認していこう。
ド・モアブルの定理より、
$$\small (\cos \theta +i\sin \theta)^5 = \cos 5\theta +i\sin 5\theta$$
(複素数の5乗が偏角の5倍になる)なので、本問では\(\small \displaystyle \theta = \frac{\pi}{3}\)としてあげればよいので、
\begin{split}
&\small \left(\cos \frac{\pi}{3}+i\sin \frac{\pi}{3}\right)^5\\
&\small =\cos \frac{5}{3}\pi+i\sin \frac{5}{3}\pi\\
&\small =\color{red}{\frac{1}{2}-\frac{\sqrt{3}}{2}i \space \cdots 【答】}\\
\end{split}
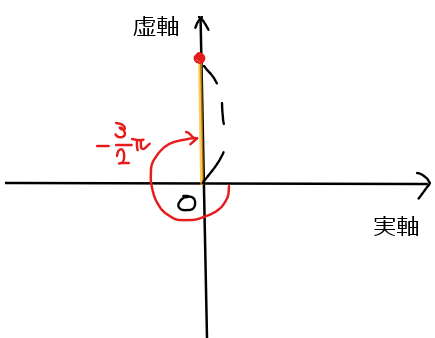
累乗がマイナスの値になっても同様にド・モアブルの定理は使うことができる。
\begin{split}
&\small \left(\cos \frac{\pi}{4}+i\sin \frac{\pi}{4}\right)^{-6}\\
&\small =\cos \left(-\frac{6}{4}\pi\right)+i\sin \left(-\frac{6}{4}\pi\right)\\
&\small =\cos \left(-\frac{3}{2}\pi\right)+i\sin \left(-\frac{3}{2}\pi\right)\\
&\small =0 + 1 \cdot i\\
&\small =\color{red}{i \space \cdots 【答】}\\
\end{split}
【問題2】複素数の\(\small n\)乗を求める問題(難易度:★☆☆)
次の式を計算せよ。
(1)\(\small \displaystyle (\sqrt{3}+i)^{9}\)
(2)\(\small \displaystyle \left(\frac{\sqrt{2}}{\sqrt{3}+i}\right)^{8}\)
(3)\(\small \displaystyle (-\sqrt{2}+\sqrt{6}i)^5\)
[(2)関西大]
※極形式への変換方法が知りたい人は「【数C_複素数平面】複素数を極形式へ変換する方法(公式不要の裏ワザ的解法)」をチェックしよう!
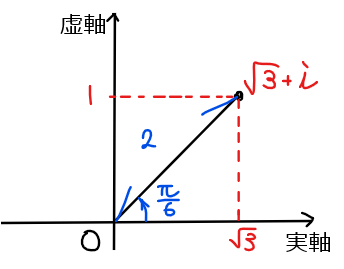
複素数 \(\small \sqrt{3}+i\)を図示すると下図のようになることから極形式で表すと
\begin{split}
\small \sqrt{3}+i = 2\left(\cos \frac{\pi}{6}+i\sin \frac{\pi}{6}\right)\\
\end{split}
となることから、ド・モアブルの定理より
\begin{split}
\small (\sqrt{3}+i)^9 &\small = \left\{2\left(\cos \frac{\pi}{6}+i\sin \frac{\pi}{6}\right)\right\}^{9}\\
&\small = 2^9\left(\cos \color{#ef5350}{\frac{9}{6}\pi}+i\sin \color{#ef5350}{\frac{9}{6}\pi}\right) \quad \color{#ef5350}{◀ 偏角を9倍}\\
&\small = 512\left(\cos \frac{3}{2}\pi+i\sin \frac{3}{2}\pi\right) \\
&\small = 512\left(0+i \cdot (-1)\right) \\
&\small = \color{red}{-512i \space \cdots 【答】}\\
\end{split}
分母の\(\small \sqrt{3}+i\)は(1)の結果から
\begin{split}
\small \sqrt{3}+i = 2\left(\cos \frac{\pi}{6}+i\sin \frac{\pi}{6}\right)\\
\end{split}
なので、
\begin{split}
\small \displaystyle \frac{\sqrt{2}}{\sqrt{3}+i} &\small = \frac{\sqrt{2}}{2\left(\cos \dfrac{\pi}{6}+i\sin \dfrac{\pi}{6}\right)}\\
&\small = \frac{1}{\sqrt{2}}\left\{\cos \left(-\dfrac{\pi}{6}\right)+i\sin\left(-\dfrac{\pi}{6}\right)\right\} \space [*1]\\
\end{split}
*1:【補足】偏角の式変形
係数部分は\(\small \displaystyle\frac{\sqrt{2}}{2}=\frac{1}{\sqrt{2}}\)と有理化しているだけ。
\begin{split}
\small \displaystyle \frac{1}{\cos \dfrac{\pi}{6}+i\sin \dfrac{\pi}{6}}\\
\end{split}
の部分については、複素数の商(割り算)は原点を中心として時計回りに偏角だけ回転するという図形的意味を持つことを考慮すると、今回は実軸上の「1」を\(\small \displaystyle -\frac{\pi}{6}\)だけ回転させた複素数になるので\(\small \displaystyle \cos \left(-\dfrac{\pi}{6}\right)+i\sin\left(-\dfrac{\pi}{6}\right)\)になる。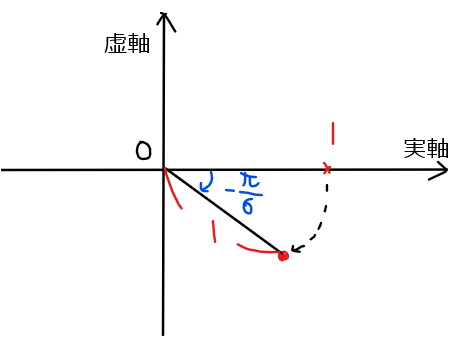
よって
\begin{split}
&\small \displaystyle \left[\frac{1}{\sqrt{2}}\left\{\cos \left(-\dfrac{\pi}{6}\right)+i\sin\left(-\dfrac{\pi}{6}\right)\right\}\right]^8\\
&\small \displaystyle =\left(\frac{1}{\sqrt{2}}\right)^8\left\{\cos \left(-\dfrac{\pi}{6}\right)+i\sin\left(-\dfrac{\pi}{6}\right)\right\}^{\color{#ef5350}8}\\
&\small \displaystyle =\frac{1}{16}\left\{\cos \left(-\dfrac{\color{#ef5350}8}{6}\pi\right)+i\sin\left(-\dfrac{\color{#ef5350}8}{6}\pi\right)\right\}\\
&\small \displaystyle =\frac{1}{16}\left\{\color{#ef5350}{\cos \left(-\dfrac{4}{3}\pi\right)+i\sin\left(-\dfrac{4}{3}\pi\right)}\right\}\\
&\small \displaystyle =\frac{1}{16}\left(\color{#ef5350}{-\frac{1}{2}+\frac{\sqrt{3}}{2}i}\right) \quad [*2]\\
&\small \displaystyle =\color{red}{-\frac{1}{32}+\frac{\sqrt{3}}{32}i \quad \cdots 【答】}\\
\end{split}
*2:【補足】極形式が表す複素数
偏角 \(\small \displaystyle -\frac{4}{3}\pi\)の符号が負なので、時計回りに回転した位置を表すことに注意して、下図の複素数を表している。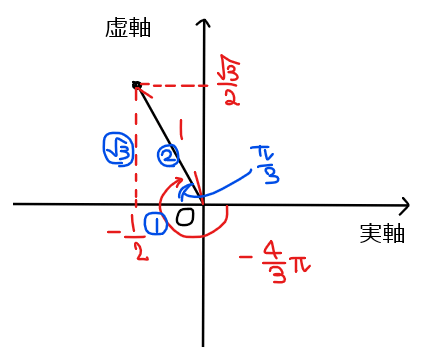
\(\small -\sqrt{2}+\sqrt{6}i\)を極形式で表すと、下図の通り原点からの距離が\(\small 2\sqrt{2}\)、偏角が\(\small \displaystyle \frac{2}{3}\pi\)なので
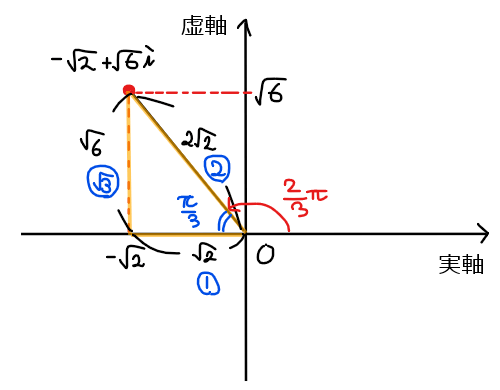
辺の比が\(\small 1: 2: \sqrt{3}\)の三角形であることに気づけるだろう。
\begin{split}
&\small \displaystyle -\sqrt{2}+\sqrt{6}i=2\sqrt{2}\left(\cos \frac{2}{3}\pi+i\sin \frac{2}{3}\pi\right)\\
\end{split}
よって、ド・モアブルの定理より
\begin{split}
&\small \displaystyle (-\sqrt{2}+\sqrt{6}i)^5\\
&\small \displaystyle =(2\sqrt{2})^5 \left(\cos \frac{2}{3}\pi+i\sin \frac{2}{3}\pi\right)^{5}\\
&\small \displaystyle =32 \cdot 4\sqrt{2} \left(\cos \left(\frac{2}{3}\pi\cdot \color{red}5\right)+i\sin \left(\frac{2}{3}\pi \cdot \color{red}5 \right) \right)\\
&\small \displaystyle =128\sqrt{2} \left(\cos \frac{10}{3}\pi+i\sin \frac{10}{3}\pi\right)\\
\end{split}
ここで、\(\small \displaystyle \frac{10}{3}\pi = 2\pi + \frac{4}{3}\pi\) なので [*1]
$$\small \displaystyle \cos \frac{10}{3}\pi+i\sin \frac{10}{3}\pi=\cos \frac{4}{3}\pi+i\sin \frac{4}{3}\pi$$
*1:【補足】三角関数の性質
角度部分が\(\small 2\pi\)を超えている(単位円上で1周以上の角度になっている)ので、\(\small 0≦ \theta <2\pi\)で表すために、\(\small 2\pi + \theta \)の形に式変形している。
なぜ\(\small 0≦ \theta <2\pi\)の範囲で角度を表すかというと、単純に角度の値が大きいと三角比の値を求めにくいからだ。三角比は\(\small \sin (2n\pi +\theta )= \sin \theta \)、\(\small \cos (2n\pi +\theta )= \cos \theta \)の式からもわかるように、角度\(\small \theta \)に対して\(\small n\)周(\(\small =2\pi \times n= 2n\pi\))しても単位円上の位置は変わらない、つまり三角比の値が同じであることから、角度部分は\(\small 0≦\theta <2\pi\)の範囲内にしておく方が計算しやすい。
ゆえに
\begin{split}
&\small \displaystyle 128\sqrt{2} \left(\cos \frac{10}{3}\pi+i\sin \frac{10}{3}\pi\right)\\
&\small \displaystyle =128\sqrt{2} \left(\cos \frac{4}{3}\pi+i\sin \frac{4}{3}\pi\right)\\
&\small \displaystyle =128\sqrt{2} \left(-\frac{1}{2}-i\frac{\sqrt{3}}{2} \right)\\
&\small \displaystyle =\color{red}{-64\sqrt{2}-64\sqrt{6}i \space \cdots 【答】}\\
\end{split}
【問題3】ド・モアブルの定理を用いた応用問題(難易度:★★☆)
\(\small \displaystyle \left(\frac{1+i}{1+\sqrt{3}i}\right)^{n}\)が実数となるような最小の自然数\(\small n\)を求めよ。
・極形式に変換していれば、虚部は\(\small \sin \theta \)と表されるので、『\(\small \sin \theta = 0\)』⇔『 \(\small \theta = m\pi\)(\(\small m\)は整数)』が偏角の条件になる。
分母、分子を極形式で表すと
\begin{split}
&\small \displaystyle 1+i = \sqrt{2}\left(\cos \frac{\pi}{4}+i\sin \frac{\pi}{4}\right)\\
&\small \displaystyle 1+\sqrt{3}i = 2\left(\cos \frac{\pi}{3}+i\sin \frac{\pi}{3}\right)\\
\end{split}
であることから、
\begin{split}
&\small \displaystyle \frac{1+i}{1+\sqrt{3}i} = \frac{\sqrt{2}\left(\cos \dfrac{\pi}{4}+i\sin \dfrac{\pi}{4}\right)}{2\left(\cos \dfrac{\pi}{3}+i\sin \dfrac{\pi}{3}\right)}\\
&\small =\frac{\sqrt{2}}{2} \left\{\cos \left(\color{red}{\dfrac{\pi}{4}-\dfrac{\pi}{3}}\right)+i\sin \left(\color{red}{\dfrac{\pi}{4}-\dfrac{\pi}{3}}\right)\right\} \space [*1]\\
&\small =\frac{\sqrt{2}}{2} \left\{\cos \left(\color{red}{-\dfrac{\pi}{12}}\right)+i\sin \left(\color{red}{-\dfrac{\pi}{12}}\right)\right\}\\
&\small =\frac{\sqrt{2}}{2} \left(\cos \dfrac{\pi}{12}-i\sin \dfrac{\pi}{12}\right)\\
\end{split}
*1:【補足】複素数の商(割り算)の計算
複素数の割り算が図形的に、原点を中心とした時計回りの回転だったことを思い出すと、\(\small \displaystyle \cos \dfrac{\pi}{4}+i\sin \dfrac{\pi}{4}\)を時計回りに\(\small \displaystyle \frac{\pi}{3}\)回転するという意味合いを持つので、偏角は\(\small \displaystyle \frac{\pi}{4}-\frac{\pi}{3}=-\frac{\pi}{12}\)となる。
割り算は偏角を引き算すると覚えておこう。
よって、ド・モアブルの定理より
\begin{split}
\small \displaystyle \left(\frac{1+i}{1+\sqrt{3}i}\right)^n &\small \small \displaystyle =\left[\frac{\sqrt{2}}{2} \left(\cos \dfrac{\pi}{12}-i\sin \dfrac{\pi}{12}\right)\right]^n\\
&\small \displaystyle =\left(\frac{\sqrt{2}}{2}\right)^n \left(\cos \dfrac{n\pi}{12}-i\sin \dfrac{n\pi}{12}\right) \space \cdots ①\\
\end{split}
ここで、①の\(\small \displaystyle \frac{\sqrt{2}}{2}\)は実数なので、\(\small \displaystyle \cos \dfrac{n\pi}{12}-i\sin \dfrac{n\pi}{12}\)が実数になれば①全体が実数となる。さらに、\(\small \displaystyle \cos \dfrac{n\pi}{12}-i\sin \dfrac{n\pi}{12}\)が実数になるためには、虚部が\(\small 0\)、すなわち
$$\small \color{#ef5350}{\sin \dfrac{n\pi}{12}=0}$$
を満たす最小の\(\small n\)を求めればよいことになる。
三角関数の性質から整数\(\small m\)(\(\small m= \cdots , -1 , 0, 1 ,2, \cdots\))に対して\(\small \sin m \pi =0\)が成り立つので、今回であれば\(\small \displaystyle \sin \color{#ef5350}{\dfrac{n}{12}}\pi\)の\(\small \dfrac{n}{12}\)が整数になるような最小の\(\small n\)を求めればよい(\(\small m\)が\(\small \dfrac{n}{12}\)に対応している)。
よって、\(\small \dfrac{n}{12}\)が整数になるためには、分母の\(\small 12\)が約分できればよく、そのような最小の自然数\(\small n\)は\(\small n= 12\)…【答】.
本記事のまとめ
今回はド・モアブルの定理の内容と典型問題の一種である複素数の累乗計算の問題について解説しました。定理自体は簡単ですが、実際の問題の中で使いこなせるように演習を重ねておきましょう。
では最後に本記事の重要ポイントを復習して終わりにしましょう。
☆重要ポイント☆
≫ ド・モアブルの定理
端的に言うと…
・複素数の\(\small n\)乗が偏角の\(\small n\)倍になるよっていう定理のこと。
厳密に言うと…
整数\(\small n\)に対して
$$\small \color{#ef5350}{(\cos \theta +i\sin \theta)^n = \cos n\theta +i\sin n\theta}$$
が成り立つ。
≫ 複素数の累乗計算
・ド・モアブルの定理を利用するために極形式に変換してから累乗する!
今回は以上です。お疲れさまでした!








コメント