【数C_複素数平面】1のn乗根を含む式の値・図形問題への応用（ド・モアブルの定理の利用）

今回は、1のn乗根を含む式の値を計算する問題について分かりやすく解説していきます。具体的には、n乗根の和や積を含んだ式の値やcosの値を求める問題、複素数平面のn乗根と平面図形の融合問題について本記事では扱います。

全体的に少し難易度は高めですが、複素数平面分野のいわゆる差がつく問題であり、難関大学を狙う人の必修科目となっているので、本記事を通して考え方のポイントを一緒に学んでいきましょう！

• 1のn乗根を含む式の値の解き方のコツを知りたい人
• 1のn乗根と図形問題の解き方のコツを知りたい人
• 定期テストや大学入試でまわりと差をつけたい人

【問題＆解説】1のn乗根を含む式の値

偏角が\(\small \displaystyle \frac{2\pi}{5}\)（1の5乗根）と\(\small \displaystyle \frac{2\pi}{7}\)（1の7乗根）を題材とした問題が頻出です。

典型問題を寄せ集めてきたので、ここにある問題が解けるようになれば、他の問題も考え方を応用することで対処できると思います。

問題の解説はこちら。

問題の解説はこちら。

問題の解説はこちら。

【基本問題】1のn乗根を含む和・積（難易度：★☆☆）

\begin{split}
\small z^5 &\small \displaystyle = \left(\cos \frac{2\pi}{5} +i\sin \frac{2\pi}{5}\right)^5\\
&\small \displaystyle = \cos \frac{2\times \color{#ef5350}5\pi}{5} +i\sin \frac{2\times \color{#ef5350}5\pi}{5} \quad ◀ ド・モアブルの定理\\
&\small \displaystyle = \cos 2\pi +i\sin 2\pi\\
&\small \displaystyle = 1\\
\end{split}

より、\(\small z\)は方程式 \(\small z^5 = 1\) を満たす。

ここで、

\begin{split}
&\small z^5=1\\
\small \Leftrightarrow \space &\small z^5-1=0\\
\small \Leftrightarrow \space &\small \color{#ef5350}{(z-1)(z^4+z^3+z^2+z+1)}=0 \quad [*1]\\
\end{split}

*1：【補足】\(\small x^n-1\)の因数分解
一般に
$$\small x^n-1=(x-1)(x^{n-1}+x^{n-2}+\cdots+x+1)$$
が成り立ちます。導出方法としては、初項\(\small 1\)、公比が\(\small x\)の等比数列の和の公式をちょっと式変形すればよくて
\begin{split}
&\small \displaystyle 1+x+x^2+\cdots+x^{n-1}=\frac{1-x^n}{1-x}\\
\small ∴ \space &\small \displaystyle (x-1)(1+x+x^2+\cdots+x^{n-1})=x^n-1\\
\end{split}
という感じで確認できます。
この公式は頻出なので覚えておきましょう！

と因数分解できることから、上記方程式の解は

\begin{cases}
\small z-1=0 \quad または\\
\small z^4+z^3+z^2+z+1=0\\
\end{cases}

となる。今回は \(\small \displaystyle z = \cos \frac{2\pi}{5} +i\sin \frac{2\pi}{5} \)より、\(\small z \neq 1\)は自明なので、\(\small z-1=0\) ⇔ \(\small z=1\)は不適。

よって

\begin{split}
&\small z^4+z^3+z^2+z+1=0
\end{split}

が成り立つ。この式を変形すると

\begin{split}
&\small z^4+z^3+z^2+z= \color{red}{-1 \space \cdots 【答】}
\end{split}

【別解】等比数列の和を利用した計算
等比数列の和の公式
\begin{split}
\small \displaystyle \sum_{k=1}^n ar^{k-1}=\frac{a(1-r^n)}{1-r}\\
\end{split}
は\(\small a,r\)が複素数の場合も使えます（複素数も実数と同じく和差積商が成り立つので同じように導出できる）。
\(\small z +z^2+z^3+z^4\)は初項\(\small z\)、公比 \(\small z\)の等比数列の和なので
\begin{split}
\small z +z^2+z^3+z^4 &\small =\frac{z(1-z^4)}{1-z}\\
&\small =\frac{z-z^5}{1-z}\\
&\small =\frac{z-1}{1-z} \quad (∵ \space z^5 =1)\\
&\small =-1\\
\end{split}
と求めることができます。

（1）でも確認した通り、\(\small z\)は5乗すると1になる（\(\small z^5=1\)が成り立つ）ことから、方程式 \(\small x^5=1\)の解である。

さらに、\(\small z^2,z^3,z^4\)についても5乗を計算すると、

\begin{split}
&\small (z^2)^5=(z^5)^2=1^2=1\\
&\small (z^3)^5=(z^5)^3=1^3=1\\
&\small (z^4)^5=(z^5)^4=1^4=1\\
\end{split}

となり、いずれも5乗すると1になるため、\(\small x^5=1\)の解である。

ここで、\(\small x^5=1\)の解はたかだか5個しかないため、\(\small z,z^2,z^3,z^4\)と\(\small 1\)（これは自明な解）の合計\(\small 5\)個がすべての解であることが求まった。

ゆえに、方程式 \(\small x^5=1\) ⇔ \(\small x^5-1=0\)を複素数の範囲で5つの解が自明になるように因数分解すると、

\begin{split}
&\small x^5 =1\\
\small \Leftrightarrow \space &\small x^5-1=0\\
\small \Leftrightarrow \space &\small (x-1)(x-z)(x-z^2)(x-z^3)(x-z^4)=0 \space \cdots ①\quad [*1]\\
\end{split}

となる。

*1：【補足】方程式の因数分解と解の値
いきなりですが、5次方程式 \(\small (x-2)(x-3)(x+1)(x-5)(x-1)=0\)の解を求めてみてください。答えは、\(\small x=2,3,-1,5,1\)です。

一般的に5次方程式の解なんて解けないことが多いのですが、この方程式が簡単に解を求めることができるのは、左辺が因数分解された形になっていたからです。皆さんは無意識的に頭の中で、『\(\small x-\alpha\)』の\(\small \alpha\)部分が解になると考えて導き出したと思います。

今回の①の式変形は端的に言うとこの逆のことをやっているだけです。今回は\(\small x^5-1=0\)の解が\(\small 1,z,z^2,z^3,z^4\)の5つだと分かっているので、あとは左辺を『\(\small x-\)（解）』の積の形にしてあげれば因数分解の完成です。

もちろん、方程式によっては実数解がない（虚数解を持つ）場合もあるワケで、たとえば、\(\small x^3-1=0\)という方程式であれば、通常は
\begin{split}
&\small (x-1)(x^2+x+1)=0\\
\end{split}
までしか因数分解できません。でも、\(\small x^2+x+1\)を複素数の範囲であえて因数分解するならば
\begin{split}
&\small \displaystyle (x-1)\left(x-\frac{-1+\sqrt{3}i}{2}\right)\left(x-\frac{-1-\sqrt{3}i}{2}\right)=0\\
\end{split}
と因数分解できます。今回の①の因数分解も\(\small z,z^2,z^3,z^4\)などは複素数なのでこんな感じの因数分解をするよ、というのが「複素数の範囲で解が自明になるように因数分解する」の意味になります。

一方で、\(\small x^5-1\)は\(\small x^5-1 = (x-1)(x^4+x^3+x^2+x+1)\)と因数分解できることから、

\begin{split}
&\small x^5 =1\\
\small \Leftrightarrow \space &\small x^5-1=0\\
\small \Leftrightarrow \space &\small (x-1)(x^4+x^3+x^2+x+1)=0 \space \cdots ②\\
\end{split}

①、②を比較することで

\begin{split}
&\small (x-1)(x^4+x^3+x^2+x+1)=(x-1)(x-z)(x-z^2)(x-z^3)(x-z^4)\\
\small \Leftrightarrow \space &\small (x^4+x^3+x^2+x+1)=(x-z)(x-z^2)(x-z^3)(x-z^4) \quad \cdots ③\\
\end{split}

が成り立つ。

あとは、③に\(\small x=1\)を代入することで、

\begin{split}
&\small 1^4+1^3+1^2+1+1=(1-z)(1-z^2)(1-z^3)(1-z^4)\\
\small \Leftrightarrow \space &\small (1-z)(1-z^2)(1-z^3)(1-z^4)=\color{red}{5\space \cdots 【答】}\\
\end{split}

\(\small z^5=1\)であることから、

\begin{split}
&\small \displaystyle \frac{1}{z+1}+\frac{1}{z^2+1}+\frac{1}{z^3+1}+\frac{1}{z^4+1}\\
&\small =\displaystyle \frac{1}{z+1}+\frac{1}{z^2+1}+\frac{\color{#ef5350}{z^2}}{(z^3+1)\color{#ef5350}{z^2}}+\frac{\color{#ef5350}{z}}{(z^4+1)\color{#ef5350}{z}}\\
&\small =\displaystyle \frac{1}{z+1}+\frac{1}{z^2+1}+\frac{z^2}{\color{#ef5350}{z^5}+z^2}+\frac{z}{\color{#ef5350}{z^5}+z}\\
&\small =\displaystyle \frac{1}{z+1}+\frac{1}{z^2+1}+\frac{z^2}{\color{#ef5350}{1}+z^2}+\frac{z}{\color{#ef5350}{1}+z}\\
&\small =\displaystyle \frac{z+1}{z+1}+\frac{z^2+1}{z^2+1}\\
&\small =\displaystyle 1+1\\
&\small =\displaystyle \color{red}{2 \space \cdots 【答】}\\
\end{split}

【標準問題】1のn乗根を含む式の値（難易度：★★☆）

\begin{split}
\small t^2 &\small \displaystyle = \left(z+\frac{1}{z}\right)^2\\
&\small \displaystyle =z^2+\frac{1}{z^2}+2\\
\end{split}

であることから、

\begin{split}
\small t^2 +t &\small \displaystyle = \left(z^2+\frac{1}{z^2}+2\right)+\left(z+\frac{1}{z}\right)\\
&\small \displaystyle = z^2+z+\frac{1}{z}+\frac{1}{z^2}+2\\
&\small \displaystyle = \frac{z^4+z^3+z+1+2z^2}{z^2}\\
&\small \displaystyle = \frac{\color{#ef5350}{z^4+z^3+z^2+z+1}+z^2}{z^2} \space \cdots ①\\
\end{split}

ここで、\(\small z^4+z^3+z^2+z+1\)は、

\begin{split}
\small z^5 &\small \displaystyle = \left(\cos \frac{2\pi}{5} +i\sin \frac{2\pi}{5}\right)^5\\
&\small \displaystyle = \cos \frac{2\times \color{#ef5350}5\pi}{5} +i\sin \frac{2\times \color{#ef5350}5\pi}{5} \quad ◀ ド・モアブルの定理\\
&\small \displaystyle = \cos 2\pi +i\sin 2\pi\\
&\small \displaystyle = 1\\
\small ∴ \space z^5 &\small \displaystyle = 1\\
\end{split}

であることから、等比数列の和の公式より

\begin{split}
\small z^4+z^3+z^2+z+1 &\small \displaystyle =\frac{1-\color{#ef5350}{z^5}}{1-z}\\
&\small \displaystyle =\frac{1-\color{#ef5350}1}{1-z}\\
&\small \displaystyle =0\\
\end{split}

なので、①に代入することで、

\begin{split}
\small t^2 +t &\small \displaystyle =\frac{\color{#ef5350}{z^4+z^3+z^2+z+1}+z^2}{z^2}\\
&\small \displaystyle =\frac{\color{#ef5350}{0}+z^2}{z^2}\\
&\small \displaystyle =\color{red}{1 \space \cdots 【答】}\\
\end{split}

\begin{split}
\small t &\small \displaystyle = z+\frac{1}{z}\\
&\small \displaystyle = z+z^{-1}\\
&\small \displaystyle = \left(\cos \frac{2\pi}{5}+i\sin \frac{2\pi}{5}\right)\\
&\small \displaystyle \quad +\left(\cos \frac{2\pi}{5}+i\sin \frac{2\pi}{5}\right)^{-1}\\
&\small \displaystyle = \left(\cos \frac{2\pi}{5}+i\sin \frac{2\pi}{5}\right)\\
&\small \displaystyle \quad +\left\{\cos \left(-\frac{2\pi}{5}\right)+i\sin\left(-\frac{2\pi}{5}\right)\right\} \space ◀ド・モアブルの定理\\
&\small \displaystyle =\cos \frac{2\pi}{5}+i\sin \frac{2\pi}{5}\\
&\small \displaystyle \quad +\cos \frac{2\pi}{5}-i\sin \frac{2\pi}{5} \quad [*1]\\
\small ∴ \space t &\small \displaystyle =2\cos \frac{2\pi}{5} \space \cdots ①\\
\end{split}

*1：【補足】三角比の性質
\(\small \cos(-\theta)=\cos \theta\)（偶関数）、\(\small \sin(-\theta)=-\sin \theta\)（奇関数）の性質を利用して式変形しています。

(1)で、\(\small t^2+t=1\)であることを求めたので、この方程式から\(\small t\)の値を求めると、

\begin{split}
&\small t^2+t-1=0\\
&\small t=\frac{-1\pm \sqrt{1^2-4\cdot 1 \cdot (-1)}}{2} \space ◀解の公式\\
\small ∴ \space &\small \displaystyle t=\frac{-1\pm \sqrt{5}}{2}\\
\end{split}

①より、\(\small \displaystyle t = 2\cos \frac{2\pi}{5} >0\)なので （[*2]）、\(\small \displaystyle t = \frac{-1-\sqrt{5}}{2} <0\)は解として不適であり、\(\small \displaystyle t = \frac{-1+\sqrt{5}}{2} >0\)が適合解となる。

*2：【補足】三角比の符号
\(\small \displaystyle \cos \frac{2\pi}{5}\)は角度が\(\small \displaystyle 0～\frac{\pi}{2}\)の範囲なので、\(\small \sin , \cos \)ともに正となります。
三角比の符号は暗記しなくても、単位円を描けば一瞬で判断できます。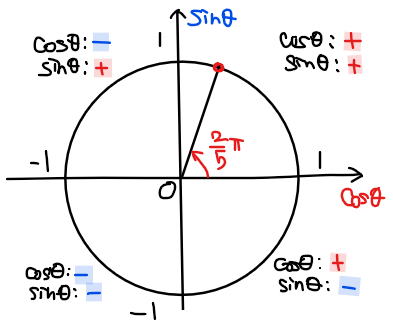

よって、

\begin{split}
&\small 2\cos \frac{2\pi}{5}=\frac{-1+\sqrt{5}}{2}\\
\small ∴ \space &\small \cos \frac{2\pi}{5}=\color{red}{\frac{-1+\sqrt{5}}{4}\space \cdots 【答】}\\
\end{split}

【応用問題】1のn乗根に関する図形問題（難易度：★★★）

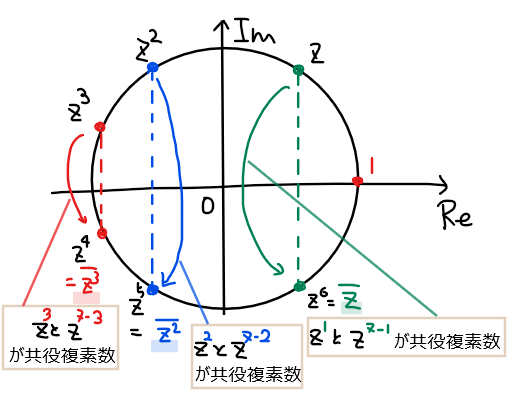
\begin{split}
&\small \displaystyle z=\cos \frac{2\pi}{7} +i\sin \frac{2\pi}{7}\\
\small \Leftrightarrow \space &\small \displaystyle z^7=\left(\cos \frac{2\pi}{7} +i\sin \frac{2\pi}{7}\right)^7\\
\small \Leftrightarrow \space &\small \displaystyle z^7=\cos 2\pi +i\sin2\pi \quad ◀ド・モアブルの定理\\
\small \Leftrightarrow \space &\small \displaystyle z^7=1 \space \cdots ①\\
\end{split}

等比数列の和の公式より

\begin{split}
&\small z+z^2+z^3+z^4+z^5+z^6\\
&\small \displaystyle =\frac{z(1-z^6)}{1-z}\\
&\small \displaystyle =\frac{z-\color{#ef5350}{z^7}}{1-z}\\
&\small \displaystyle =\frac{z-\color{#ef5350}1}{1-z} \quad (∵ \space ①)\\
&\small \displaystyle =\color{red}{-1 \space \cdots 【答】}\\
\end{split}

\(\small w\)の和に含まれない\(\small z^3,z^5,z^6\)について、

\begin{split}
\small z^3 &\small = \left(\cos \frac{2\pi}{7} +i\sin \frac{2\pi}{7}\right)^3\\
&\small = \cos \frac{6\pi}{7} +i\sin \frac{6\pi}{7}\\
&\small = \cos \left(2\pi -\frac{8\pi}{7}\right) +i\sin\left(2\pi -\frac{8\pi}{7}\right) \quad [*1]\\
&\small = \cos \left(-\frac{8\pi}{7}\right) +i\sin\left(-\frac{8\pi}{7}\right)\\
&\small = \cos \frac{8\pi}{7} -i\sin\frac{8\pi}{7}\\
&\small = \left(\cos \frac{2\pi}{7} -i\sin\frac{2\pi}{7}\right)^4\\
&\small = \bar{z}^4\\
\small ∴ \space &\small z^3 =\bar{z}^4 \space \cdots ②\\
\end{split}

*1：【補足】偏角の式変形について
偏角 \(\small \displaystyle \frac{6\pi}{7} = 2\pi -\frac{8\pi}{7}\)の式変形について、この式自体は、
\begin{split}
\small 2\pi -\frac{8\pi}{7} &\small = \frac{14\pi-8\pi}{7}\\
&\small = \frac{6\pi}{7}\\
\end{split}
なので、成り立つことは分かるかと思います。では、なぜ急にこのような式変形をしたのか説明しましょう。あえて『\(\small 2\pi\)』を作り出す式変形をすることで、三角比の性質
\begin{cases}
\small \cos(\theta + 2\pi)= \cos \theta \\
\small \sin(\theta + 2\pi)= \sin \theta \\
\end{cases}
（1周しても三角比の値は変わらない）が使えるので、
\begin{split}
\small \cos \color{red}{\frac{6\pi}{7}}=\cos \left(2\pi -\frac{8\pi}{7}\right) &\small = \cos \color{blue}{\frac{8\pi}{7}}\\
\end{split}
のように\(\small \color{red}{\theta} \)の偏角を\(\small \color{blue}{2\pi – \theta}\)の偏角に変換することができます。\(\small \sin\)の場合も、符号は変わりますが
\begin{split}
\small \sin \color{red}{\frac{6\pi}{7}}&\small =\sin \left(2\pi -\frac{8\pi}{7}\right) \\
&\small = \sin\left(-\frac{8\pi}{7}\right) \space ◀\sin (2\pi +\theta )=\sin \thetaの利用\\
&\small = -\sin\color{blue}{\frac{8\pi}{7}}\\
\end{split}
のように、偏角は同様に置き換えできます。
このような変形をしておくことで、\(\small z^4,z^5,z^6\)の複素数の偏角を、\(\small z,z^2,z^3\)の複素数の偏角だけで表すことができ、後ほどの式変形で効果を発揮します。

同様に、\(\small z^5\), \(\small z^6\)についても計算すると、

\begin{split}
\small z^5 &\small = \left(\cos \frac{2\pi}{7} +i\sin \frac{2\pi}{7}\right)^5\\
&\small = \cos \frac{10\pi}{7} +i\sin \frac{10\pi}{7}\\
&\small = \cos \left(2\pi -\frac{4\pi}{7}\right) +i\sin\left(2\pi -\frac{4\pi}{7}\right) \\
&\small = \cos \left(-\frac{4\pi}{7}\right) +i\sin\left(-\frac{4\pi}{7}\right)\\
&\small = \cos \frac{4\pi}{7} -i\sin\frac{4\pi}{7}\\
&\small = \left(\cos \frac{2\pi}{7} -i\sin\frac{2\pi}{7}\right)^2\\
&\small = \bar{z}^2\\
\small ∴ \space &\small z^5 =\bar{z}^2 \space \cdots ③\\
\end{split}

\begin{split}
\small z^6 &\small = \left(\cos \frac{2\pi}{7} +i\sin \frac{2\pi}{7}\right)^6\\
&\small = \cos \frac{12\pi}{7} +i\sin \frac{12\pi}{7}\\
&\small = \cos \left(2\pi -\frac{2\pi}{7}\right) +i\sin\left(2\pi -\frac{2\pi}{7}\right) \\
&\small = \cos \left(-\frac{2\pi}{7}\right) +i\sin\left(-\frac{2\pi}{7}\right)\\
&\small = \cos \frac{2\pi}{7} -i\sin\frac{2\pi}{7}\\
&\small = \bar{z}\\
\small ∴ \space &\small z^6 =\bar{z} \space \cdots ④\\
\end{split}

よって、②～④より

\begin{split}
\small \bar{w} &\small = \bar{z}+\bar{z}^2+\bar{z}^4\\
&\small = z^6+z^5+z^3 \space \cdots ⑤\\
\end{split}

なので、

\begin{split}
\small w+\color{#ef5350}{\bar{w}} &\small = (z+z^2+z^4)+\color{#ef5350}{(z^6+z^5+z^3)} \space (∵ \space ⑤)\\
&\small = z+z^2+z^3+z^4+z^5+z^6\\
&\small = \color{red}{-1 \space \cdots 【答】}\\
\end{split}

ただし最後の式変形は（1）の結果、\(\small z+z^2+z^3+z^4+z^5+z^6=-1\)を用いた。

続いて \(\small w \bar{w}\)も計算すると（頑張って展開…）

\begin{split}
\small w \bar{w}&\small = (z+z^2+z^4)(z^6+z^5+z^3)\\
&\small = z^4(1+z+z^3)(1+z^2+z^3)\\
&\small = z^4\{1\cdot (1+z^2+z^3)+z (1+z^2+z^3)+z^3(1+z^2+z^3)\}\\
&\small = z^4(1+z^2+z^3+z+z^3+z^4+z^3+z^5+z^6)\\
&\small = z^4(\color{#ef5350}{1+z+z^2+z^3+z^4+z^5+z^6}+2z^3)\\
&\small = z^4(\color{#ef5350}{0}+2z^3) \quad [*2]\\
&\small = 2 \color{#ef5350}{z^7}\\
&\small = 2\cdot \color{#ef5350}1 \quad (∵ \space ①より z^7=1)\\
&\small = \color{red}{2 \space \cdots 【答】}\\
\end{split}

*2：【補足】\(\small 1+z+z^2+z^3+z^4+z^5+z^6\)の値
（1）で求めた \(\small z+z^2+z^3+z^4+z^5+z^6=-1\)の右辺を左辺に移項すれば\(\small 1+z+z^2+z^3+z^4+z^5+z^6=0\)となることが分かります。
あるいは、1の\(\small n\)乗根の解をすべて足すと0になるということを覚えておいてもよいかもしれません。

\(\small \mathrm{△P_1P_2P_4}\)の各頂点の複素数は\(\small \mathrm{P_1}(z),\) \(\small \mathrm{P_2}(z^2),\) \(\small \mathrm{P_4}(z^4)\) であることから、重心 \(\small \mathrm{Q}(\alpha)\)は、

\begin{split}
\small \alpha &\small = \frac{z+z^2+z^4}{3}\\
\small ∴ \space \alpha &\small = \frac{w}{3} \space \cdots ⑥ \quad [*1]\\
\end{split}

同様に、\(\small \mathrm{△P_3P_5P_6}\)の各頂点の複素数は\(\small \mathrm{P_3}(z^3),\) \(\small \mathrm{P_5}(z^5),\) \(\small \mathrm{P_6}(z^6)\) であることから、重心 \(\small \mathrm{R}(\beta)\)は、

\begin{split}
\small \beta &\small = \frac{z^3+z^5+z^6}{3}\\
\small ∴ \space \beta &\small = \frac{\bar{w}}{3} \space \cdots ⑦ \quad (∵ ⑤)\\
\end{split}

*1：【補足】座標平面と複素数平面の対応関係
座標平面上の\(\small \mathrm{△P_1P_2P_4}\)の重心\(\small \mathrm{Q}(x,y)\)の座標は、3点の座標を \(\small \mathrm{P_1}(x_1,y_1),\) \(\small \mathrm{P_2}(x_2,y_2),\) \(\small \mathrm{P_4}(x_4,y_4)\) とすると、
\begin{split}
\small \mathrm{Q} \left(\frac{x_1+x_2+x_4}{3},\frac{y_1+y_2+y_4}{3}\right)
\end{split}
（＝3つの座標の平均）だったことを思い出すと、今回の場合は座標平面上での\(\small x\)座標を複素数平面上での実部、\(\small y\)座標を虚部に対応させることで同様に考えることができる。
つまり、複素数平面上の\(\small \mathrm{△P_1P_2P_4}\)の重心\(\small \mathrm{Q}\)の複素数\(\small \alpha =x+iy\)は、3点の複素数を \(\small \mathrm{P_1}(z=x_1+iy_1),\) \(\small \mathrm{P_2}(z^2=x_2+iy_2),\) \(\small \mathrm{P_4}(z^4=x_4+iy_4)\) とすると、
\begin{split}
\small \alpha = \frac{x_1+x_2+x_4}{3}+\frac{y_1+y_2+y_4}{3}i
\end{split}
と表すことができる。このことから、上式を式変形することで
\begin{split}
\small \alpha &\small = \frac{x_1+x_2+x_4}{3}+\frac{y_1+y_2+y_4}{3}i\\
&\small = \frac{(x_1+iy_1)+(x_2+iy_2)+(x_4+iy_4)}{3}\\
&\small = \frac{z+z^2+z^4}{3}\\
\end{split}
となるので、解答のように3点の複素数を足して3で割り算することで、座標平面のときと同じように重心の複素数を求められることが分かる。

⑥、⑦で重心の複素数を\(\small w \)および\(\small \bar{w}\)を用いて表すことができたので、あとは、\(\small w\)の値を求めることができれば、重心の複素数を求めることができる。そして、\(\small w\)の値は、（2）の結果である

\begin{cases}
\small w + \bar{w} = -1\\
\small w \bar{w} = 2\\
\end{cases}

に着目すると、\(\small w\)と\(\small \bar{w}\)の和と積の値が分かっているので、解と係数の関係を使ってあげれば求めることができそうだ。

すなわち、\(\small w\)と\(\small \bar{w}\)は2次方程式

\begin{split}
\small t^2+t+2=0\\
\end{split}

の解として与えられる（ここでは変数に使う文字を \(\small t\)としているが、文字は何でもOK）[*2]。

*2：【補足】2次方程式と解と係数の関係
2次方程式 \(\small ax^2+bx+c=0\)（ただし\(\small a \neq 0\)）の2つの解が\(\small \alpha,\beta\)であるとき、解と係数の関係より
\begin{cases}
\small \displaystyle \alpha +\beta = -\frac{b}{a}\\
\small \displaystyle \alpha \beta =\frac{c}{a}\\
\end{cases}
が成り立つことを利用すると、\(\small a = 1\)のとき
\begin{cases}
\small \displaystyle b = -(\alpha +\beta)\\
\small \displaystyle c =\alpha \beta\\
\end{cases}
のように2次方程式の係数 \(\small a,b,c\)を決定させることができる。

本問であれば、2次方程式の係数は \(\small a =1\), \(\small b=-(w+\bar{w})=1\), \(\small c=w\bar{w}=2\)と決定できる。

2次方程式を解の公式を用いて解くと、

\begin{split}
\small \displaystyle t = \frac{-1\pm\sqrt{7}i}{2} \space \cdots ⑧\\
\end{split}

なので、この2解が\(\small w\)と\(\small \bar{w}\)となるが、最後に、2解のうちどちらが\(\small w\)あるいは\(\small \bar{w}\)であるかを確認する。

2解を判別する相違点は、虚部の正負であることに着目すると、\(\small w\)の虚部は

\begin{split}
\small \displaystyle \mathrm{Im}(w) &\small =\mathrm{Im}(z+z^2+z^4)\\
&\small \displaystyle =\sin \frac{2\pi}{7} +\sin\frac{4\pi}{7}+\sin \frac{8\pi}{7}\\
&\small \displaystyle =\sin \frac{2\pi}{7} +\sin\frac{4\pi}{7}-\sin \frac{\pi}{7} \quad [*3]\\
\end{split}

*3：【補足】\(\small \sin (\pi+\theta)=-\sin \theta\)を利用
今確認したいのは、\(\small w\)の虚部の符号なワケだが、2行目の式を見ると角度が\(\small 0～\pi\)の範囲では\(\small \sin\)の値は正のため、第1、2項目は正、第3項目は負になり、おそらく\(\small w\)の虚部としては、全体としては正であることが予想できる。
そこで、うまく正になることを示したいので、*3の式変形では第3項目の角度を \(\small \displaystyle \frac{8\pi}{7}=\pi +\frac{\pi}{7}\)と変形して、\(\small \sin (\pi+\theta)=-\sin \theta\)の公式を適用することで、まずは第3項目が負であることが明確になるように式変形している。

あとは、第3項目のマイナスをうまく処理することで『（正の値）+（正の値）=（正の値）』という論法で正になることを示す方針で考える。

ここで、\(\small \sin\)の値の引き算を一つにまとめる公式（積和の公式）

\begin{split}
\small \displaystyle \sin \mathrm{A}-\sin \mathrm{B}=2 \cos \frac{\mathrm{A}+\mathrm{B}}{2}\sin \frac{\mathrm{A}-\mathrm{B}}{2} \quad [*4]\\
\end{split}

を用いて、\(\small \displaystyle \sin\frac{4\pi}{7}-\sin \frac{\pi}{7} \)部分をまとめると

\begin{split}
\small \displaystyle \sin\frac{4\pi}{7}-\sin \frac{\pi}{7} &\small =2 \cos \frac{\dfrac{4\pi}{7}+\dfrac{\pi}{7}}{2} \sin \frac{\dfrac{4\pi}{7}-\dfrac{\pi}{7}}{2}\\
&\small =2 \cos \frac{5\pi}{14} \sin \frac{3\pi}{14}\\
\end{split}

*4：【補足】積和の公式は暗記不要
\(\small \sin \)や\(\small \cos\)の和・差を積に変換する公式として積和の公式が有名ですが、かなり複雑な式であり暗記する気力がおきない…と悩んでいる人もいいのではないでしょうか？
でも、実は積和の公式は暗記しなくても簡単に導出できます。
覚えておくのは、「加法定理から導出できる」ということだけ。たとえば、今回のみたいに\(\small \sin\)の差を積に変換したい場合は、\(\small \sin\)の加法定理、
\begin{split}
\small \sin(\alpha +\beta)=\sin\alpha \cos \beta+\cos\alpha \sin\beta\\
\small \sin(\alpha -\beta)=\sin\alpha \cos \beta-\cos\alpha \sin\beta\\
\end{split}
の2つの式を書いてあげて\(\small \sin\)の差なので、引き算します。
すると、
\begin{split}
\small \sin(\alpha +\beta)-\sin(\alpha -\beta)=2\cos\alpha \sin\beta \space \cdots (*)\\
\end{split}
のように第2項目だけが残るので、後は角度部分を
\begin{cases}
\small \mathrm{A} = \alpha +\beta\\
\small \mathrm{B} =\alpha -\beta\\
\end{cases}
と置き直してあげれば、
\begin{cases}
\small \displaystyle \alpha = \frac{\mathrm{A} +\mathrm{B}}{2}\\
\small \displaystyle \beta = \frac{\mathrm{A} -\mathrm{B}}{2}\\
\end{cases}
となるので、これを\(\small (*)\)に代入することで積和の公式を導くことができました。

\(\small \displaystyle 0< \frac{5\pi}{14} <\frac{\pi}{2}\)より、\(\small \displaystyle \cos \frac{5\pi}{14}>0\)、\(\small \displaystyle 0< \frac{3\pi}{14} <\pi\)より、\(\small \displaystyle \sin \frac{3\pi}{14}>0\)であることから、\(\small \displaystyle 2 \cos \frac{5\pi}{14} \sin \frac{3\pi}{14}>0\)なので、\(\small \displaystyle \sin\frac{4\pi}{7}-\sin \frac{\pi}{7}>0 \space \cdots ⑨\)。

ゆえに、[*3]は、第1項目が\(\small \displaystyle \sin\frac{2\pi}{7}>0\)なので正、第2、3項目も⑨より正であることから、『（正の値）+（正の値）=（正の値）』なので、

\begin{split}
\small \displaystyle \sin \frac{2\pi}{7} +\sin\frac{4\pi}{7}-\sin \frac{\pi}{7} >0.\\
\end{split}

よって、\(\small w= z+z^2+z^4\)の虚部が正の値であることが分かったので、⑧の\(\small t\)の値のうち虚部が正となるものが\(\small w\)になる。

ゆえに、

\begin{split}
\small \displaystyle w= \frac{-1+\sqrt{7}i}{2}\\
\end{split}

共役複素数\(\small \bar{w}\)は

\begin{split}
\small \displaystyle \bar{w}= \frac{-1-\sqrt{7}i}{2}\\
\end{split}

これらの結果を⑥、⑦に代入することで、重心の複素数は

\begin{split}
\small \displaystyle \alpha &\small = \frac{w}{3}\\
\small ∴ \space \color{red}{\alpha} &\small =\color{red}{\frac{-1+\sqrt{7}i}{6} \space \cdots 【答】}\\
\end{split}

\begin{split}
\small \displaystyle \beta &\small = \frac{\bar{w}}{3}\\
\small ∴ \space \color{red}{\beta} &\small =\color{red}{\frac{-1-\sqrt{7}i}{6} \space \cdots 【答】}\\
\end{split}

複素数 \(\small \mathrm{Q}(\alpha) ,\mathrm{R}(\beta)\)は、実部が同じであることから、線分\(\small \mathrm{QR}\)は実軸に対して垂直であることに注意して\(\small \mathrm{△P_0QR}\)を図示すると下図の通り。

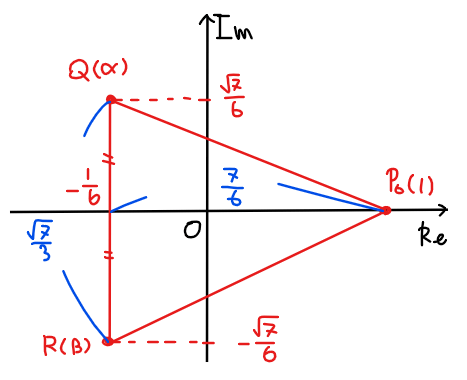
よって、\(\small \mathrm{△P_0QR}\)の面積は

\begin{split}
\small \displaystyle \mathrm{△P_0QR} &\small =\frac{1}{2}\times \frac{\sqrt{7}}{3}\times \frac{7}{6}\\
&\small =\color{red}{\frac{7\sqrt{7}}{36} \space \cdots 【答】}\\
\end{split}

本記事のまとめ

今回は1の\(\small n\)乗根を含む式の値を求める問題と、その発展問題として平面図形との融合問題について解説してみました。少しコツをつかむまでは難しく感じるかもしれませんが、式変形のパターンがある程度決まっているので、ポイントを押さえてしまえば同じような考え方で解ける問題が多いので、今回の問題の解き方をしっかりと復習しておきましょう。

では、最後に本記事のポイントをおさらいして終わりにしましょう。

☆重要ポイント☆
≫ 1の\(\small n\)乗根を含む式の値の求め方
① 因数分解の利用
$$\small x^n-1=(x-1)(x^{n-1}+x^{n-2}+\cdots+x+1)$$
② 1の\(\small n\)乗根の定義の利用
$$\small z^n=1 $$
③ \(\small x^n=1\)の方程式の解 \(\small 1,z,z^2,\cdots z^{n-1}\)が満たす関係式の利用
$$\small x^n-1=(x-1)(x-z)(x-z^2)\cdots(x-z^{n-1})=0$$

≫ 1の\(\small n\)乗根の図形的位置関係
・1の\(\small n\)乗根の解は、\(\small \{z^m,z^{n-m}\}\)が互いに共役複素数になる。
$$\small \displaystyle z^{n-m}=\overline{z^m}$$
このことは、1の\(\small n\)乗根が複素数平面上で、1を出発点として円周上に等間隔に並ぶことを覚えておけば、実軸に対して線対称な位置関係にある\(\small z^m\)と\(\small z^{n-m}\)が共役複素数であると気づくことができる。

今回は以上です。お疲れさまでした！