今回は複素数を極形式で表す方法について解説していきます。
突然ですが皆さんは『\(\small 1+i\)』を極形式で表すことができますか?そもそも極形式って何だっけ?という人や複雑な式変形や公式を駆使して極形式に変換した人もいるかもしれません。
でも実は複素数を極形式に変換するためには、特別な式変形や公式を覚えなくても図と三角比の基礎知識さえあれば簡単に求めることができます。
そこで、本記事では公式を使わずに極形式に変換する裏ワザ的解法と極形式が役立つ場面について徹底解説していきます。ぜひ最後まで一緒に確認していきましょう!
- そもそも極形式とはなにかについて知りたい人
- 極形式が使える場面について知りたい人
- 公式不要な極形式の変換方法について知りたい人
- 定期テスト対策、受験対策がしたい人
【基礎講義】複素数の極形式
【講義1】極形式とは?
まずはじめに今回のメインテーマである極形式とは何かについて解説しておきます。
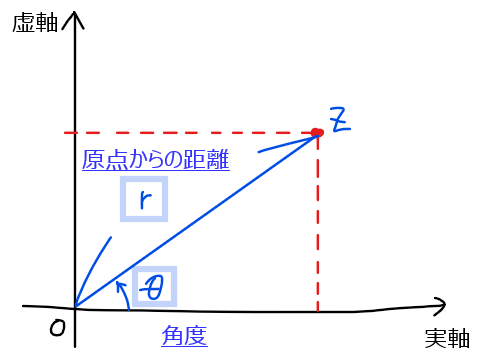
これまで複素数といったら、\(\small 2-3i\)や\(\small \displaystyle \frac{1}{2}+\sqrt{3}i\)のように、『(実部)\(\small +\)(虚部)\(\small i\)』の形で表していました。まぁ複素数は実数と虚数を組み合わせた数であるということから考えると至極まっとうな表記方法ですよね。実部を\(\small x\)、虚部を\(\small y\)とすれば一般に\(\small x+iy\)と表現できます。
一方で、極形式は原点からの距離と実軸からの角度(偏角)で表現する方法です。まずはこれまでとは少し異なった表現方法なんだなということを押さえておきましょう。
では極形式で複素数を表したときの一般形(\(\small x+iy\)に相当するもの)はどのような形で書けるのか次章で確認していきます。
【講義2】極形式の一般形(公式)
ではさっそく極形式で複素数がどう表せるのか求めていきましょう。極形式で複素数を表すとは、すなわち『原点からの距離』と『実軸からの角度(偏角)』の2つだけを使って複素数を表すということに注意しましょう。この2つ以外の文字は使ってはいけません。
なんだか難しそうに感じますが、図を描いて考えれば意外と簡単に求めることができます。
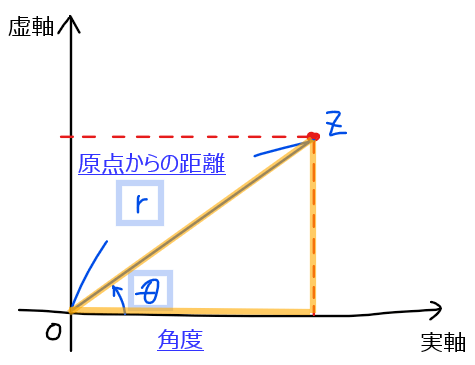
まず上図のように複素数\(\small z\)がある場合、原点からの距離 \(\small r\)と実軸との角度 \(\small \theta\)は図の通りになります。ここで、黄色の三角形に着目すると斜辺が\(\small r\)、1角が \(\small \theta\)の直角三角形ができるので、三角関数を用いることで実軸と虚軸の値(直角三角形の残り縦横の長さ)を求めることができます(下図参照)。
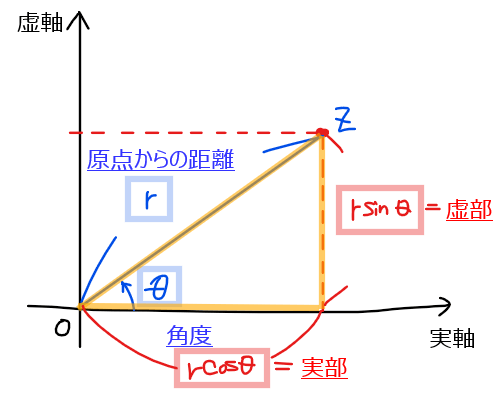
【補足】極形式と極座標表示
原点からの距離と角度を使って平面上の1点を表す…。この考え方、どこかで見覚えはないでしょうか?実は、円の媒介変数表示でおなじみの極座標表示と同じ考え方ですね。
\begin{cases}
\small x = r\cos\theta\\
\small y = r\sin\theta\\
\end{cases}
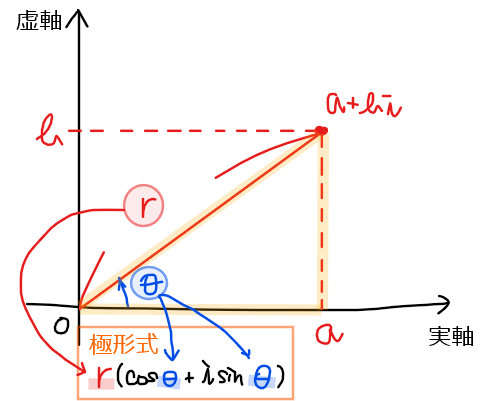
よって、複素数\(\small z\)は実部が\(\small r\cos\theta\)、虚部が\(\small r\sin\theta\)の複素数となるので、
\begin{split}
\small z &\small= r\cos\theta +i(r\sin\theta)\\
&\small= \color{#ef5350}{r(\cos\theta +i\sin\theta)}\\
\end{split}
のように表すことができます。
この式は、もともと求めたかった『原点からの距離( \(\small =r\))』と『実軸からの角度( \(\small = \theta\))』の2つだけを使って複素数を表しているので、これが極形式の一般形になります。
$$\small \color{#ef5350}{r(\cos\theta +i\sin\theta)}$$
【講義3】[裏ワザあり]極形式を求める3STEP
最後に複素数を極形式に変換する方法を解説します。では、実際の例題を通して解説していきます。
複素数 \(\small z = 1 + \sqrt{3}i\)を極形式で表せ。ただし偏角は\(\small 0≦\theta < 2\pi\)とする。
☞ 複素数\(\small z=x+iy\)の原点からの距離は \(\small |z|=\sqrt{x^2+y^2}\)
・極形式の公式の括弧内にある三角関数を満たす偏角 \(\small \theta \)を求める。
\(\small 1+\sqrt{3}i\)の原点からの距離は、\(\small |z|=\sqrt{1^2+(\sqrt{3})^2}=2\)であることから、全体を\(\small 2\)で括り出すと
\begin{split}
\small z &\small= 1+\sqrt{3}i\\
&\small= \color{#ef5350}2\left(\frac{1}{\color{#ef5350}2}+\frac{\sqrt{3}}{\color{#ef5350}2}i\right)\\
\end{split}
上式と極形式の公式 \(\small r(\cos\theta+i\sin\theta)\)を見比べると、\(\small r = 2\)、三角関数部分については、
\begin{cases}
\small \displaystyle \cos\theta = \frac{1}{2}\\
\small \displaystyle \sin\theta = \frac{\sqrt{3}}{2}\\
\end{cases}
となることから、上記を満たす角度\(\small \theta \)は\(\small \displaystyle \theta=\frac{\pi}{3} \)と求めることができる。
よって、問題の複素数を極形式で表すと \(\small \displaystyle 2\left(\cos \frac{\pi}{3}+i\sin\frac{\pi}{3} \right)\)…【答】となる。
***
上記が一般的な複素数を極形式に変換する解法ですが、上記の解法は極形式を意識して意図的な式変形をしていく必要があるため、変形の難易度がやや高いなぁと感じる人も多いと思います。
そこでここからは図を描くことで極形式に変換する裏ワザ的解法を紹介していこうと思います。
・STEP2:斜辺の長さを求める(三平方の定理)
・STEP3:実軸からの角度を求める(三角比)
では先程の例題の場合で実際の使い方を確認していきましょう!
≪図を用いた裏ワザ的解法≫
まずは変換したい複素数 \(\small 1+ \sqrt{3}i\)を複素数平面上に図示します。
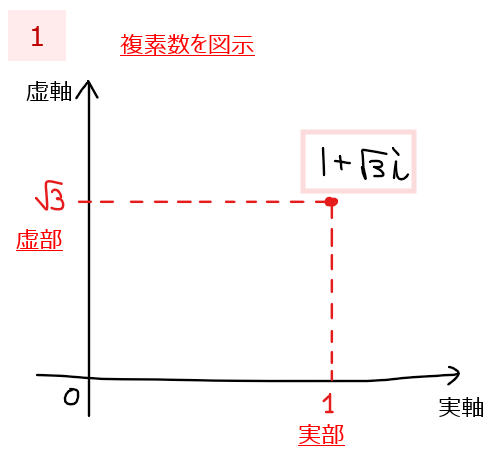
次に斜辺の長さ(=原点からの距離)を求めます。これは、図示した三角形を見れば三平方の定理から、\(\small \sqrt{1^2+(\sqrt{3})^2}=\sqrt{4}=2\)と求められます。
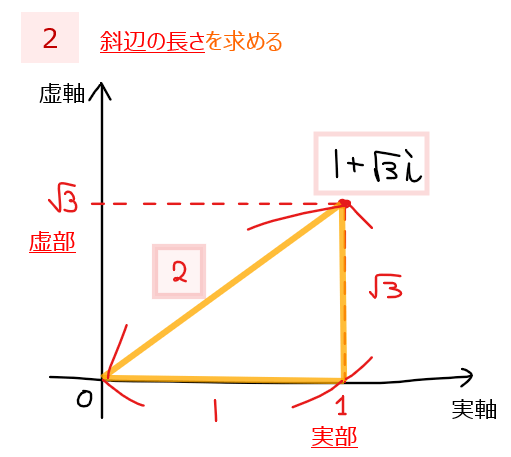
最後に三角形の各辺の比から実軸と斜辺の角度(=偏角)を求めます。今回であれば辺の比が\(\small 1 :2:\sqrt{3}\)の三角形なので角度は\(\small \displaystyle \frac{\pi}{3}\)であることが分かります。
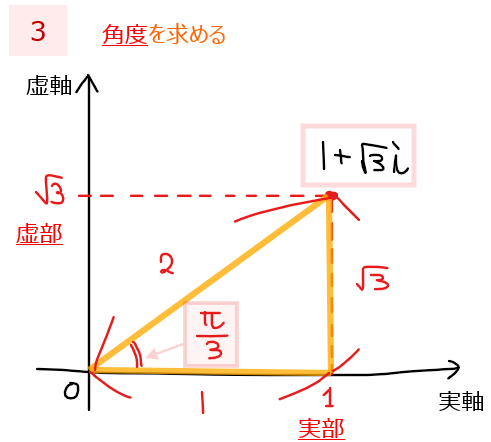
よって、STEP2で求めた原点からの距離 \(\small 2\)とSTEP3で求めた偏角 \(\small \displaystyle \frac{\pi}{3}\)から極形式は、\(\small \displaystyle 2\left(\cos \frac{\pi}{3}+i\sin\frac{\pi}{3} \right)\)…【答】であることが求まります。
この解法であれば、複雑は式変形を回避しながら、原点との距離と偏角を求めることができるため、おすすめの解法になります。
例題では偏角が\(\small \displaystyle 0≦ \theta ≦\frac{\pi}{2}\)の場合でしたが、\(\small \displaystyle \frac{\pi}{2}< \theta\)の場合でも同じように求めることができます。
詳しくはこのあとの問題演習の中で解説していきます。
【講義4】極形式ってなんで必要?
ここまででなんとなく極形式についてわかってきたところで、この章ではそもそもなんで極形式を考えるのかについて簡単に解説しておきます。
極形式とは、複素数を「原点からの距離」と「実軸からの角度」で表す表記方法であると言いました。では原点からの距離や角度で表すのでしょうか?
実は、複素数の計算をするうえで積や商は図形的に回転・拡大(縮小)という意味を持ちます。回転は角度、拡大や縮小は原点からの距離が長くなったり短くなったりする移動のことなので、原点からの距離と偏角に注目した極形式の表記をしておくと、かけ算や割り算がとても簡単に計算できます。
たとえば、\(\small \displaystyle \left(\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}}i \right)^{100}\)の計算をしたい場面を考えてみます。普通に計算すると100乗はさすがに計算できませんよね…。
でも\(\small \displaystyle \frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}}i\)を
$$\small \frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}}i=\cos \frac{\pi}{4}+i\sin \frac{\pi}{4}$$
のように極形式で表すと、原点からの距離が1、偏角が\(\small \displaystyle \frac{\pi}{4}\)の複素数と分かるので、複素数のかけ算では原点からの距離はかけ算、偏角は足し算になる性質を利用すると、原点からの距離は\(\small 1^{100}=1\)、偏角は\(\small \displaystyle \frac{\pi}{4}\times 100 = 25\pi\)とすぐに計算できるので、計算結果は
\begin{split}
&\small \displaystyle \left(\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}}i \right)^{100}\\
&\small \displaystyle = \cos 25\pi +i\sin 25\pi\\
&\small = -1\\
\end{split}
と求めることができます。
このように複素数の積や商を計算するときには、複素数の原点からの距離と偏角が重要になってくるので、極形式にして計算することで非常に威力を発揮します。
【問題&解説】複素数を極形式に変換する問題
【基本問題】\(\small a+bi\)型の複素数の極形式
次の複素数を極形式で表せ。ただし、偏角\(\small \theta \)は\(\small 0≦\theta < 2\pi\)とする。
(1)\(\small \sqrt{3}+3i\)
(2)\(\small -1+i\)
(3)\(\small -2i\)
問題の複素数を図示すると下図の通り。
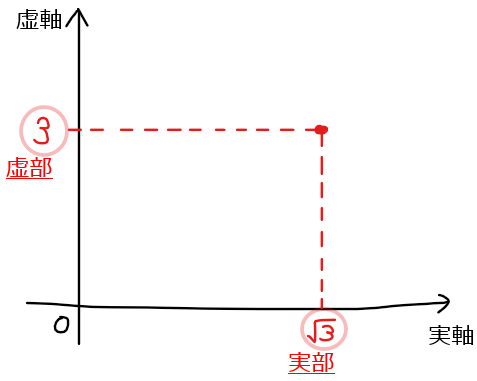
次に原点と複素数を結んでできる三角形に着目して斜辺と偏角を求めると
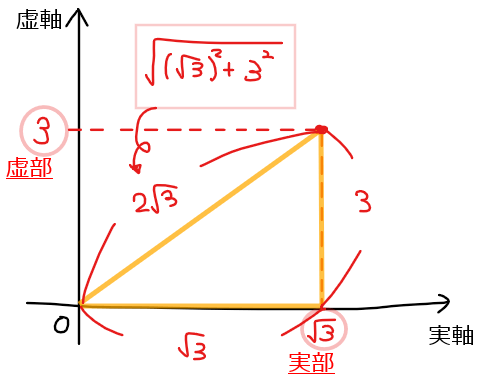
斜辺は三平方の定理から\(\small \sqrt{(\sqrt{3})^2+3^2}=\sqrt{12}=\color{red}{2\sqrt{3}}\)…①と求まる。
偏角を求めるときには、三角形の辺の比を確認して\(\small 1:2:\sqrt{3}\)(30° or 60°の三角形)なのか\(\small 1:1:\sqrt{2}\)(45°の三角形)のどちらになるのかを確認すればよいだろう。
今回は辺の比が少し分かりにくいが、全部の辺を\(\small \sqrt{3}\)で割り算すると\(\small 1:2:\sqrt{3}\)の三角形になっていることが分かる。
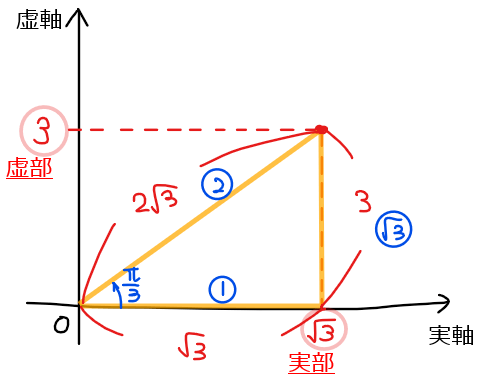
よって、偏角は \(\small \displaystyle \frac{\pi}{3}\)…②と求まる。
①、②より、原点からの距離が\(\small 2\sqrt{3}\)、偏角が\(\small \displaystyle \frac{\pi}{3}\)の複素数であることから極形式は、\(\small \displaystyle 2\sqrt{3}\left(\cos \frac{\pi}{3}+i\sin \frac{\pi}{3}\right)\)…【答】.
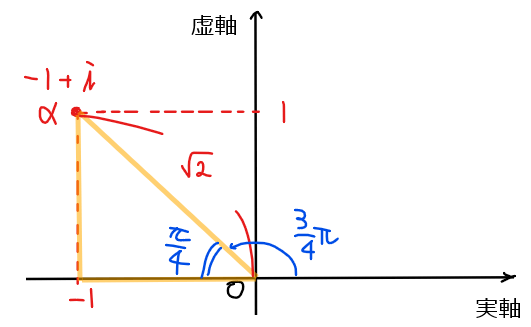
まずは、複素数\(\small -1+i\)を複素数平面上に図示する。
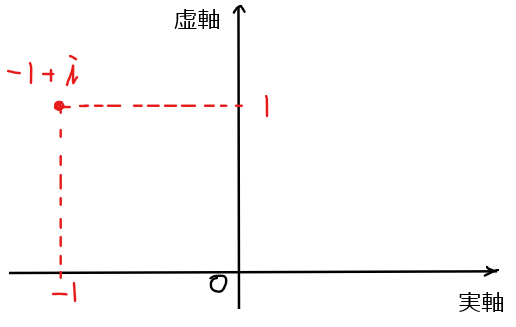
今回は実部が負なので、考えるべき三角形は以下のようになることに注意する[*1]。
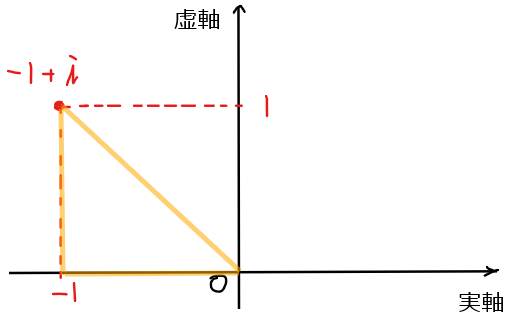
*1:【補足】考える三角形に注意
極形式に変換するときに考える三角形は、必ず実軸と斜辺を2辺に持つ三角形で考えることに注意しましょう。単位円で三角比を考えるときと同じですね。
よって、斜辺の長さは\(\small \sqrt{(-1)^2+1^2}=\color{red}{\sqrt{2}}\)、偏角は\(\small 1:1:\sqrt{2}\)の三角形なので、\(\small \displaystyle \pi – \frac{\pi}{4}=\color{red}{\frac{3}{4}\pi}\) [*2]。
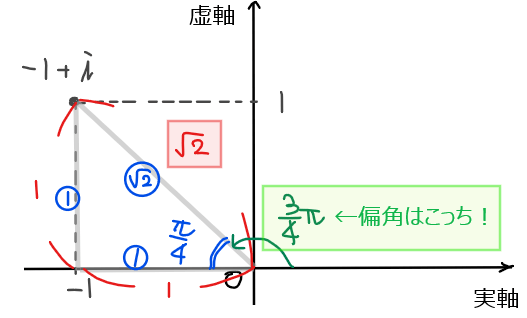
*2:【補足】偏角の求め方
三角関数を含む方程式を解くときに使う単位円と同様に、角度は必ず実軸の正の部分から計った角度になることに注意。
以上より、原点からの距離が\(\small \sqrt{2}\)、偏角が\(\small \displaystyle \frac{3}{4}\pi\)の複素数であることから極形式は、\(\small \displaystyle \sqrt{2}\left(\cos \frac{3}{4}\pi+i\sin \frac{3}{4}\pi \right)\)…【答】.
\(\small -2i\)は実部が\(\small 0\)、虚部が\(\small -2\)であることから、複素数平面上では以下のように虚軸上に位置する。
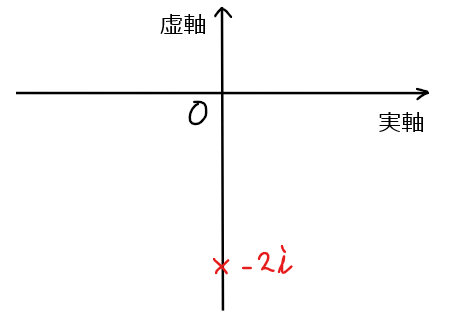
虚軸上にあるため三角形はできないが、単位円で三角比の値を求めるときと同じ考え方で、原点からの距離と偏角をそれぞれ確認しておこう。
まず原点からの距離は、図から\(\small 2\)…①とすぐ求まる。
次に偏角を確認していく。偏角 \(\small \theta \)とは『実軸の正の部分からの反時計回りの角度』という意味だったことを思い出すと、問題の条件である偏角の範囲が\(\small 0≦ \theta <2\pi\)とは、実軸正の部分から反時計回りに一周する範囲で角度を表せというのが今回の偏角の範囲になる [*1]。
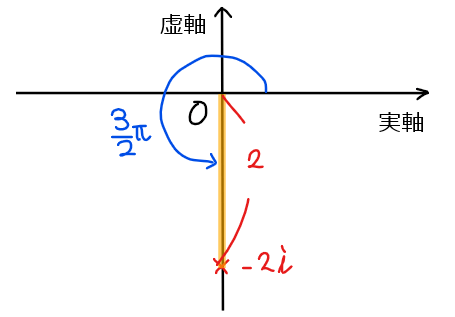
*1:【補足】偏角の範囲について
多くの問題では偏角 \(\small \theta \)は\(\small 0≦ \theta <2\pi\)の範囲となることが多いが稀に\(\small -\pi≦ \theta <\pi\)のように異なる範囲が指定されることがあるので注意が必要。
仮に本問の偏角を\(\small -\pi≦ \theta <\pi\)の範囲で表すのであれば、\(\small \displaystyle -\frac{\pi}{2}\)(時計回りに\(\small 90°\)の位置)となる。
よって、偏角は\(\small \displaystyle \color{red}{\frac{3}{2}\pi}\)(時計回り\(\small 270°\)の位置)…②。
①、②より、原点からの距離が\(\small 2\)、偏角が\(\small \displaystyle \frac{3}{2}\pi\)の複素数であることから極形式は、\(\small \displaystyle 2\left(\cos \frac{3}{2}\pi+i\sin \frac{3}{2}\pi \right)\)…【答】.
【標準問題】複素数の積・商の極形式
次の複素数を極形式で表せ。ただし、偏角\(\small \theta \)は\(\small 0≦\theta < 2\pi\)とする。
(1)\(\small \displaystyle \frac{2+3i}{5+i}\)
(2)\(\small \alpha = -1+i\), \(\small \beta = \sqrt{3}+i\)のとき、\(\small \displaystyle \alpha\beta, \frac{\alpha}{\beta} \)
Ⅰ.極形式に変換可能
・計算前に極形式に変換してから図形的な性質(回転・拡大)を利用して解く
Ⅱ.極形式に変換不可
・有理化・展開して\(\small a+bi\)型にしてから極形式に変換
極形式に変換するにはまず複素数を複素数平面上に図示する必要があるわけだが、問題の複素数は分数型になっておりこのままだと実部と虚部が分からず図示できない。分母分子の複素数も極形式に変換できそうにはないことから、まずは有理化して\(\small a+bi\)型に変形する。
\begin{split}
\small \displaystyle \frac{2+3i}{5+i} &\small =\frac{(2+3i)\color{#ef5350}{(5-i)}}{(5+i)\color{#ef5350}{(5-i)}}\\
&\small \displaystyle =\frac{13+13i}{25+1}\\
&\small \displaystyle =\frac{13(1+i)}{26}\\
&\small \displaystyle =\frac{1}{2}(1+i) \quad \cdots ①\\
\end{split}
先頭に\(\small \displaystyle \frac{1}{2}\)がついていて少し分かりにくいが、展開したら\(\small \displaystyle \frac{1}{2}+\frac{1}{2}i\)となることから、\(\small a+bi\)型に変形できた。
このあと原点からの距離と偏角を求める際には全体を\(\small \displaystyle \frac{1}{2}\)で括った①の形にしておいて括弧内の\(\small 1+i\)を極形式に変換して最後に\(\small \displaystyle \frac{1}{2}\)を掛け算する方が計算が簡単なので、①の括弧内を極形式に変換することを考える。
\(\small 1+i\)を図示して原点からの距離と偏角を求めると下図のようになることから、極形式では
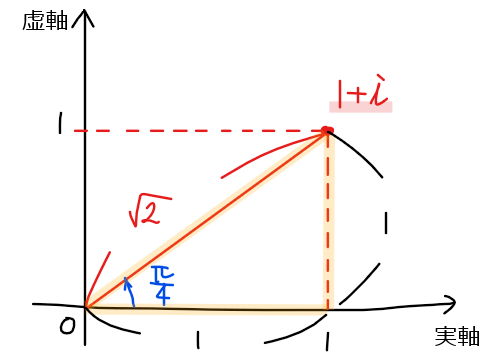
$$\small \displaystyle 1+i = \color{red}{\sqrt{2}}\left(\cos \color{blue}{\frac{\pi}{4}}+i\sin \color{blue}{\frac{\pi}{4}}\right) \quad \cdots ②$$
と表すことができる。
最後に②を①に代入することで求める複素数の極形式は、\(\small \displaystyle \frac{\sqrt{2}}{2}\left(\cos \frac{\pi}{4}+i\sin \frac{\pi}{4} \right)\)…【答】.
それぞれの複素数 \(\small \alpha, \beta\)は実部・虚部を見ると\(\small \pm1, \space \sqrt{3}\)などから構成されており極形式に変換できそうな複素数である。
そこでまずはそれぞれを極形式に変換しておく。
\begin{split}
\small \alpha &\small =-1+i\\
&\small \displaystyle =\sqrt{2}\left(\cos \frac{3}{4}\pi + i \sin \frac{3}{4}\pi \right) \quad \cdots ①\\
\end{split}
\begin{split}
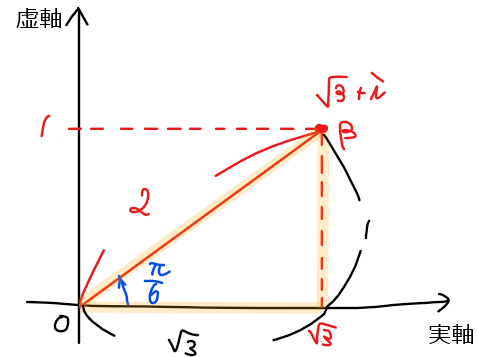
\small \beta &\small =\sqrt{3}+i\\
&\small \displaystyle =2\left(\cos \frac{\pi}{6} + i \sin \frac{\pi}{6}\right) \quad \cdots ②\\
\end{split}
あとは、複素数の積・商が図形的な回転・拡大(縮小)の意味合いを持つことを利用して\(\small \alpha\beta\)や\(\small \displaystyle \frac{\alpha}{\beta}\)の極形式を計算すればよい(複素数の積・商の図形的意味合いについて詳しい解説は「【数C_複素数平面】複素数の回転・拡大と極形式」を確認しよう!)。
≫ \(\small \alpha\beta\)(複素数の積)の計算
複素数同士を掛け算すると
・原点からの距離:それぞれの積
・偏角:それぞれの和
になることを利用すると、①、②の結果から、\(\small \alpha \beta\)の原点からの距離は\(\small 2\sqrt{2}\)、偏角は\(\small \displaystyle \frac{3}{4}\pi+\frac{\pi}{6}=\)\(\small \displaystyle \frac{11}{12}\pi\)になる。
よって、極形式は\(\small \displaystyle \alpha \beta=\color{red}{2\sqrt{2}\left(\cos \frac{11}{12}\pi+i\sin \frac{11}{12}\pi \right)}\) …【答】.
≫ \(\small \displaystyle \frac{\alpha}{\beta}\)(複素数の商)の計算
複素数同士を割り算すると
・原点からの距離:それぞれの商
・偏角:それぞれの差
になることを利用すると、①、②の結果から、\(\small \displaystyle \frac{\alpha}{\beta}\)の原点からの距離は\(\small \displaystyle \frac{\sqrt{2}}{2}\)、偏角は\(\small \displaystyle \frac{3}{4}\pi-\frac{\pi}{6}=\)\(\small \displaystyle \frac{7}{12}\pi\)になる。
よって、極形式は\(\small \displaystyle \frac{\alpha}{\beta}=\color{red}{\frac{\sqrt{2}}{2}\left(\cos \frac{7}{12}\pi+i\sin \frac{7}{12}\pi \right)}\) …【答】.
【補足】極形式に変換してから積・商を計算する理由
解き方として、\(\small \alpha\beta\)や\(\small \displaystyle \frac{\alpha}{\beta}\)を計算して\(\small a+bi\)の形にしてから極形式にする解法ではダメなのでしょうか?
結論、その解法では解けない問題があります。なぜならば偏角がうまく求められない場合があるからです。今回の問題がその典型例で、たとえば積を計算してから極形式に変換しようとすると
\begin{split}
\small \alpha\beta &\small =(-1+i)(\sqrt{3}+i)\\
&\small \displaystyle =(-\sqrt{3}-1)+(\sqrt{3}-1)i\\
\end{split}
となりますが、実部と虚部が我々の知っている三角比ではないため詰んでしまいます…。
なぜこんなことが起きるのかというと、実は計算前の時点では各々の複素数の偏角は\(\small 30°\)と\(\small 135°\)という見慣れた角度なのですが、積をとると\(\small 30°+135°= 165°\)という未知の角度になってしまい三角比の値から角度を特定できなくなることが原因です。
そのため、複素数の積・商を計算するときには、既知の三角比になっているうちに個々の複素数を極形式に変換しておくことがポイントになります。
【応用問題】三角関数を含む複素数の極形式
次の複素数を極形式で表せ。ただし、偏角\(\small \theta \)は\(\small 0≦\theta < 2\pi\)とする。
(1)\(\small -\sin \alpha + i\cos \alpha \)(\(\small 0 ≦ \alpha < 2\pi\))
(2)\(\small -\cos \alpha + i\sin \alpha \)(\(\small 0 ≦ \alpha < 2\pi\))
☞ 三角形の角度が\(\small 0°\)~\(\small 90°\)の間でないと図形的な考察がしにくいので、\(\small \displaystyle 0<\alpha <\frac{\pi}{2}\)の範囲で\(\small \sin \alpha\)や\(\small \cos \alpha\)の符号に注意して図示する。
・偏角 \(\small \theta \)を求めたら、\(\small 0 ≦ \theta < 2\pi\)の範囲であるかの確認を行う。
☞ 範囲外になっている場合は偏角に\(\small 2\pi\)を足し引きして調整すればOK。
一般的には、極形式の基本形 \(\small r(\cos \theta+i \sin \theta)\)と比較して\(\small r, \space \theta\)を特定するという数式変形を駆使した解法が紹介されるが、三角比の角度に関する諸公式が完璧に頭に入っていないと詰んでしまう。
ここで紹介する解法では図形的な考察から解く方法を紹介しているので、公式を忘れてしまった場合や検算の際に是非活用してみてほしい。
図形的な考察をするためにまずは\(\small \displaystyle 0< \alpha <\frac{\pi}{2}\)の範囲に限定して複素数を図示することを考える。
\(\small \displaystyle 0< \alpha <\frac{\pi}{2}\)の範囲では、\(\small \cos \alpha >0\)、\(\small \sin \alpha >0\)なので、問題の複素数 \(\small -\sin \alpha + i\cos \alpha\)の実部は負、虚部は正になることに注意して図示すると下図のようになる。
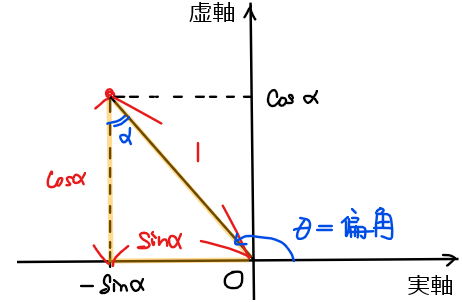
原点からの距離は、三角形の斜辺になるので\(\small \sqrt{(-\sin \alpha)^2+\cos^2 \alpha}=1\)とすぐ求めることができる。
次に偏角については実軸正の部分からの角度となるが、三角形の角度に着目すると複素数が位置する角度はちょうど\(\small \alpha\)になる [*1]ことから、三角形の図形問題を解く要領で偏角 \(\small \theta\)は\(\small \displaystyle \theta =\frac{\pi}{2}+\alpha \)(三角形の一つの外角はそれと隣り合わない二つの内角の和に等しい)と求めることができる。
*1:【補足】三角形の角度の計算
慣れないうちは少し分かりにくいかもしれないが、下図のように角度を\(\small x\)とおいて三角比の定義に当てはめて考えると\(\small x=\alpha\)になることが分かる。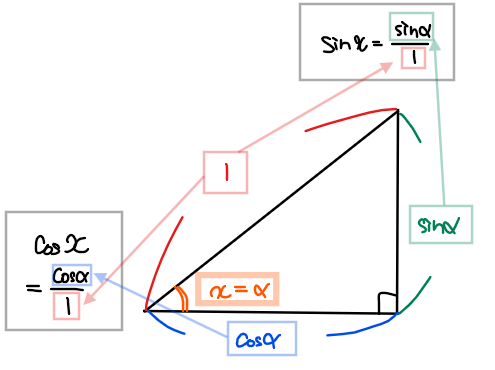
よって、原点からの距離が1、偏角が\(\small \displaystyle \alpha + \frac{\pi}{2}\)なので、極形式は\(\small \displaystyle \cos \left(\frac{\pi}{2}+\alpha\right)+i\sin \left(\frac{\pi}{2}+\alpha\right) \)…①となる。
ただし①が成り立つのはあくまで\(\small \displaystyle 0< \alpha <\frac{\pi}{2}\)の範囲であることに注意が必要。そのほかの範囲では原点からの距離は変わらないが偏角が\(\small 0≦\theta < 2\pi\)の範囲内にあるか確認する必要がある。
そこで\(\small \displaystyle \alpha + \frac{\pi}{2}\)が取り得る範囲を確認すると
\begin{split}
\small 0≦ &\small \alpha <2\pi\\
\small \Leftrightarrow \space 0+\color{#ef5350}{\frac{\pi}{2}}≦ &\small \alpha +\color{#ef5350}{\frac{\pi}{2}}<2\pi+\color{#ef5350}{\frac{\pi}{2}}\\
\small \Leftrightarrow \space \frac{\pi}{2}≦ &\small \alpha +\frac{\pi}{2}<\frac{5}{2}\pi\\
\end{split}
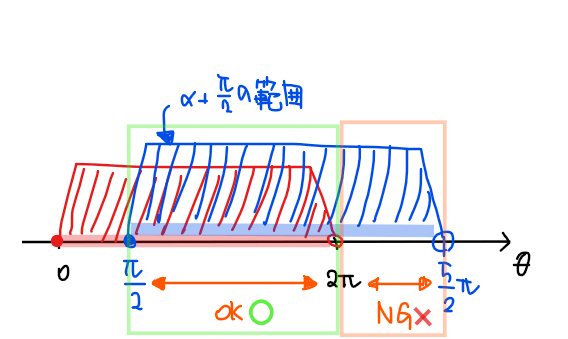
この範囲を見ると、上図の赤線範囲が偏角\(\small \displaystyle 0≦ \theta <2\pi\)の範囲なので
\(\small \displaystyle \frac{\pi}{2}≦\alpha +\frac{\pi}{2} <2\pi\)は範囲内 …(A)
一方で、赤線範囲外となっている
\(\small \displaystyle 2\pi≦ \alpha +\frac{\pi}{2} < \frac{5}{2}\pi\)は範囲外 …(B)
になっている。
範囲外になっている(B)については、範囲外だから不適…とするのではなく、三角比の角度は\(\small \cos(\theta +2n\pi)=\cos \theta\)のように\(\small 2\pi\)の周期をずらしても同じ値(単位円上で一周したら同じ値)であることに注意すると\(\small \displaystyle 0≦ \theta <2\pi\)の範囲内となるように角度を調整してあげればよい。
今回の場合であれば\(\small \displaystyle 2\pi≦ \alpha +\frac{\pi}{2} < \frac{5}{2}\pi\)は、\(\small \displaystyle 0≦ \theta <2\pi\)の範囲を超えて2周目に突入してしまっているので、\(\small 2\pi\)だけ引き算して1周分前に戻してあげればよいだろう。
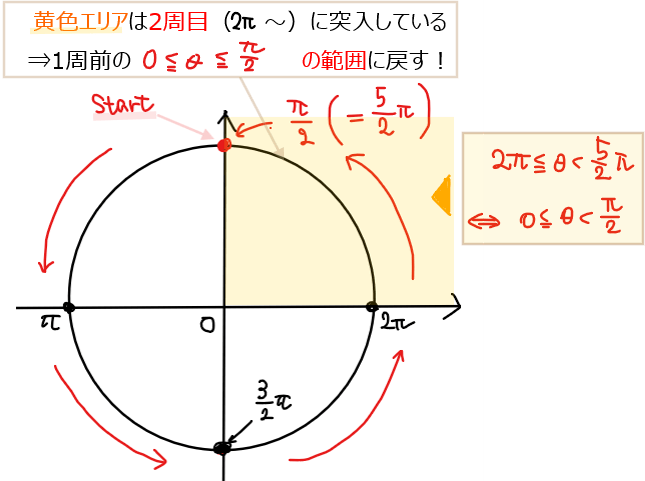
つまり偏角は
$$\small \displaystyle \left(\alpha +\frac{\pi}{2}\right)-2\pi = \color{#ef5350}{\alpha -\frac{3}{2}\pi}$$
としておけばよい。
以上をまとめると、(A)の範囲、すなわち
\begin{split}
\small \displaystyle \frac{\pi}{2}≦ &\small \alpha +\frac{\pi}{2} <2\pi\\
\small \Leftrightarrow \space \displaystyle \color{red}{0≦ }&\small \color{red}{\alpha <\frac{3}{2}\pi}\\
\end{split}
の範囲では極形式は\(\small \displaystyle \cos \left(\alpha + \frac{\pi}{2}\right)+i\sin \left(\alpha + \frac{\pi}{2}\right) \) …【答】となり、(B)の範囲、すなわち
\begin{split}
\small \displaystyle 2\pi≦ &\small \alpha +\frac{\pi}{2} <\frac{5}{2}\pi\\
\small \Leftrightarrow \space \displaystyle \color{red}{\frac{3}{2}\pi≦ }&\small \color{red}{\alpha <2\pi}\\
\end{split}
の範囲では極形式は\(\small \displaystyle \cos \left(\alpha -\frac{3}{2}\pi \right)+i\sin \left(\alpha -\frac{3}{2}\pi \right) \) …【答】となる。
\(\small \displaystyle 0< \alpha <\frac{\pi}{2}\)の範囲では、問題の複素数 \(\small -\cos \alpha + i\sin \alpha\)の実部は負、虚部は正になることに注意して図示すると下図のようになる。
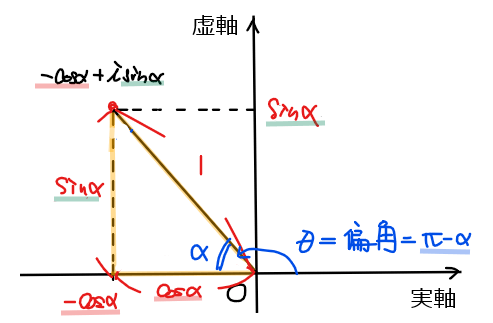
図示した三角形から、原点との距離が1、原点が位置する角度が\(\small \alpha\)になるので、偏角は\(\small \theta = \pi – \alpha\)と求めることができる。
偏角の値が取り得る範囲を確認すると
\begin{split}
\small 0≦ &\small \alpha <2\pi\\
\small \Leftrightarrow \space -2\pi < &\small -\alpha ≦0\\
\small \Leftrightarrow \space \color{#ef5350}{\pi}-2\pi < &\small \color{#ef5350}{\pi}-\alpha ≦\color{#ef5350}{\pi}\\
\small \Leftrightarrow \space -\pi< &\small \pi-\alpha ≦\pi\\
\end{split}
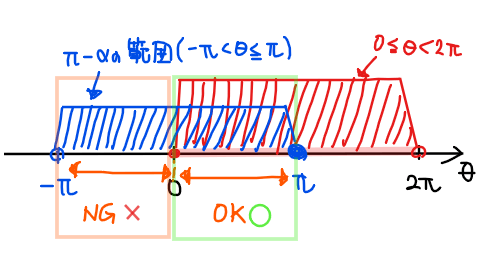
よって、偏角の範囲が\(\small 0≦ \pi-\alpha ≦\pi\)、すなわち\(\small 0≦ \alpha ≦\pi\)のときは偏角\(\small \theta = \pi -\alpha\)が \(\small 0≦\theta<2\pi\)の範囲内なので、極形式は \(\small \cos (\pi -\alpha)+i\sin (\pi -\alpha)\)…【答】となる。
一方で、偏角の範囲が\(\small -\pi< \pi-\alpha <0\)、すなわち\(\small \pi< \alpha <2\pi\)のときは偏角\(\small \theta = \pi -\alpha\)が\(\small 0≦\theta<2\pi\)の範囲より小さい範囲に外れいている(\(\small -\pi< \theta <0\)なので)ので、1周分足し算してあげれば\(\small 0≦\theta<2\pi\)の範囲内に含められる。
よって、偏角に\(\small 2\pi\)を足し算することで、\(\small (\pi -\alpha)+2\pi =3\pi-\alpha \)とすればよい。
ゆえに、\(\small \pi< \alpha <2\pi\)のとき、極形式は \(\small \cos (3\pi -\alpha)+i\sin (3\pi -\alpha)\)…【答】となる。
本記事のまとめ
今回は複素数を極形式に変換する方法について解説していきました。極形式は複素数の最重要分野と言っても過言ではない非常によく使う考え方になるので、変換方法はもちろん、本記事で紹介した裏ワザ的解法を利用して素早く変換できるように何度も練習を重ねておきましょう。
では最後に本記事のポイントを復習して終わりにしましょう。
☆本記事のポイント☆
・極形式とは、複素数を『原点からの距離』と『実軸からの角度(偏角)』を使って表すこと。
・極形式への変換は、複素数平面上に複素数を図示して原点からの距離と偏角を図形的に求めるのがおすすめ!
・極形式は、複素数の積や商を計算する際に便利な表記方法。
今回は以上です。お疲れさまでした!






コメント