【数Ⅰ】2次関数を平行移動した式を求める公式（なぜマイナスになるのか分かりやすく解説）

2次関数を\(\small x\)軸方向に\(\small p\)、\(\small y\)軸方向に\(\small q\)だけ平行移動した式を求めよ、といった問題でこんな疑問を抱いたことはないでしょうか？

なんで\(\small x\)軸方向に\(\small p\)移動しているのに\(\small x\color{red}{-p}\)のようにマイナス符号が付くのか？

今回はそんな疑問について、なるべく数学の小難しい説明を使わずに分かりやすく解説していこうと思います。

そして、本記事の後半では平行移動を駆使して2次関数の式を求める問題について解説していますので、苦手を克服したい人や自分の実力を試してみたい人はぜひ最後まで問題にチャレンジしてみてください！

　本記事はこんな人におすすめ

平行移動の公式の符号にマイナスが付く理由について理解したい人
2次関数を平行移動や対称移動した式の求め方について知りたい人
共通テスト対策、定期テスト対策がしたい人

　本記事のレベル

重要度

低

余力あれば

普通

必須

高
難易度

易しい

易

やや易

やや難

難

難しい
暗記/理解

暗記重視

暗記

半々

理解

理解重視

【基礎講義】平行移動の考え方
1. 【講義1】平行移動の公式
2. 【講義2】なぜ符号がマイナスになるのか？
【問題＆解説】平行移動に関する問題
本記事のまとめ

【基礎講義】平行移動の考え方

【講義1】平行移動の公式

平行移動の公式について解説する前に、まず平行移動とは何かについて簡単に復習しておきましょう。

平行移動とは、向きが変わらないような縦方向や横方向へのグラフ移動という意味です。縦方向と横方向の移動だけ考えて斜め方向の移動は考えないの？と思った人もいるかもしれないですが、斜め方向への移動は結局は縦移動と横移動の組み合わせなので縦横方向の移動だけを考えればOKという言うわけです！

逆に、向きが変わるような反転や回転は平行移動とは言いません。

では、ここからが本題です。平行移動の公式を確認していきましょう。

Point：平行移動した式の求め方

\(\small x\)軸方向（横方向）に\(\small p\)、\(\small y\)軸方向（縦方向）に\(\small q\)平行移動した関数の式を求めたければ、\(\small x\)を\(\small x-p\)、\(\small y\)を\(\small y-q\)に置き換えせよ！

説明だけだと分かりにくいと思うので、具体例で解説します。

例題１：平行移動した式の求め方

\(\small y=x^2+1\)を\(\small x\)軸方向に\(\small 3\)、\(\small y\)軸方向に\(\small -2\)だけ平行移動した式を求めよ。

（解説＆解答）
Pointの内容に当てはめてあげると、\(\small p=3\)、\(\small q = -2\)に対応するので、\(\small x\)を\(\small x-3\)、\(\small y\)を \(\small y-(-2)=y+2\)に置き換えてあげることで
\begin{split}
&\small \color{#ef5350}{y+2}=\color{#ef5350}{(x-3)}^2+1\\
\small \Leftrightarrow \space &\small y=(x-3)^2-1\\
\small \Leftrightarrow \space &\small \color{red}{y=x^2-6x+8 \space \cdots 【答】}\\
\end{split}

【講義2】なぜ符号がマイナスになるのか？

平行移動した式の求め方は分かったかと思いますが、ここからはなぜ符号にマイナスが付くのか？もう少し正確にいえば、なぜ移動方向と符号が逆転するのか？という理由について『直感的な説明』と『数学的な説明』の2パターンで説明していきたいと思います。数学の細かい説明が苦手だけど理由が知りたいという人は『直感的な説明』を、厳密な説明じゃないと納得できないという人は『数学的な説明』を中心に確認してみましょう！

　≫大前提　
大前提として、点の移動と式の移動は根本的に異なることを認識しておくとこのあとの説明が分かりやすくなると思います（個人的にはこのポイントについては教科書等でもあまり触れられていないのかなと思っています…）。

何を言っているのか分からないと思うので、かみ砕いて説明しますね。例えば点\(\small (1,2)\)を\(\small x\)軸方向に2、\(\small y\)軸方向に\(\small -3\)だけ平行移動した場合、移動後の点の座標は\(\small (3,-1)\)になります。これは皆さんの感覚と同じように移動した分、座標が増減しています。これは点自体の移動だからというのがポイントです。

一方で、式（グラフ・関数）の平行移動は、\(\small y = x^2+3x+1\)の移動のように具体的な点ではなく\(\small x\)や\(\small y\)といった変数の移動です。変数は基準点である原点（\(\small x=0,y=0\)の点）の位置によって値が決まるので、変数が移動するということは原点が移動するということになります（詳細は「直感的な説明」の方で解説します）。

なので、式の平行移動とは変数の移動であり、変数の移動とは基準点の移動ということを頭の片隅に置いておきましょう。

　≫直感的な説明　
符号が逆転する理由を端的に説明するならば、基準点の移動によって、各点の位置関係は逆方向に移動することになるからです。

たとえば、今皆さんの手元に1枚の宝の地図があるとします。その地図には『海賊船がある場所から東に3km、北に4km進んだところに宝箱がある』と書かれていたとします。

ここで、海賊船が波に流されて東に1km、北に1km平行移動してしまったとします。このとき、宝箱は今いる海賊船からどのくらいの位置にあるでしょうか？

落ち着いて考えればすぐ分かると思いますが、答えは『東に2km、北に3km』の位置になります。もともと宝箱があった『東に3km、北に4km』の位置から北東に1kmずつ移動しているからといって、それぞれ+1kmして『東に4km、北に5km』とはなりません。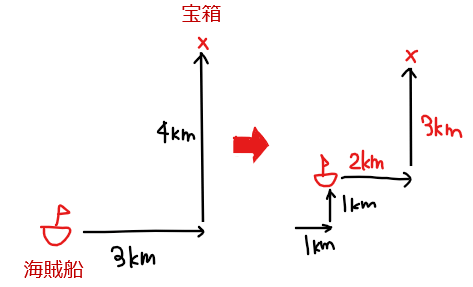

このように、海賊船という基準点（関数の場合は原点）が平行移動したことで、宝箱がある点の位置は逆方向に移動することになります。つまり、基準となる海賊船の位置がずれることで宝箱の位置自体は変わらないものの海賊船からの位置関係は変わることが分かります。

最後にこの考え方を例題1のグラフに当てはめて考えてみます。\(\small x,y\)方向にそれぞれ\(\small +3, -2\)だけグラフを平行移動するという操作は、見方を変えると原点を\(\small x,y\)方向にそれぞれ\(\small -3, +2\)だけ平行移動すると考えることもできます。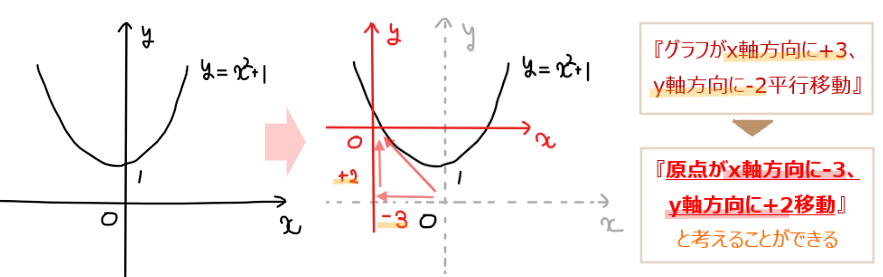

このように考えると、各点\(\small (x,y)\)自体は原点が移動した分、\(\small (x-3,y+2)\)のように位置関係が変わることになります。

　≫数学的な説明　
では、例題1の状況を例として、数式を使ったちょっと真面目な説明もしておきます。
関数は無数の点の集合なので、平行移動を考えるときには特定の点の移動について考えて、それが他の点にも同じように適用できるという説明の流れで考えると分かりやすいでしょう。

というわけで、まずは\(\small y=x^2+1\)上のとある点\(\small \mathrm{P}(x_1, y_1)\)が例題1のような平行移動をして点\(\small \mathrm{Q}(x_2, y_2)\)に移動したとします。このとき、\(\small x_1,x_2,y_1,y_2\)の関係としては、
\begin{split}
\begin{cases}
\small x_2=x_1+3\\
\small y_2=y_1-2\\
\end{cases}
\small \quad \cdots ①
\end{split}
が成り立ちます。ここまでは符号が感覚と一致していると思います。

ここから、移動後の点\(\small \mathrm{Q}(x_2, y_2)\)が満たす関係式が求めたい式になるので、\(\small x_2,y_2\)の関係式を求めていきます。

ここで、\(\small \mathrm{P}(x_1, y_1)\)は\(\small y=x^2+1\)上の点だったので、当然
\begin{split}
&\small y_1=x_1^2+1 \space \cdots ②
\end{split}
が成り立ちます。

すると、①の関係式を
\begin{cases}
\small x_1=\color{#ef5350}{x_2-3}\\
\small y_1=\color{#ef5350}{y_2+2}\\
\end{cases}
と変形したうえで（ここで符号が逆転する）、②に代入することで
\begin{split}
&\small \color{#ef5350}{(y_2+2)}=\color{#ef5350}{(x_2-3)}^2+1\\
\small \Leftrightarrow \space &\small y_2=(x_2^2-6x_2+9)-1\\
\small \Leftrightarrow \space &\small y_2=x_2^2-6x_2+8\\
\end{split}
の関係式が得られます。

今は特定の点\(\small \mathrm{P}(x_1, y_1)\)を点\(\small \mathrm{Q}(x_2, y_2)\)へ移動する場合を考えましたが、これは点\(\small \mathrm{P}\)がどんな値であっても成り立ちます。つまり、移動先の点\(\small \mathrm{Q}\)もどんな点であっても成り立つので、特定の点を表す\(\small x_2, y_2\)という表記をすべての実数を表す\(\small x,y\)に置き換えた\(\small y=x^2-6x+8\)が平行移動後の式を表す関数になるわけです。

【問題＆解説】平行移動に関する問題

基本問題

（1）\(\small x\)軸方向に\(\small -1\)、\(\small y\)軸方向に\(\small 2\)だけ平行移動すると放物線 \(\small y=x^2+3x+4\) に移されるような放物線の方程式を求めよ。
（2）放物線 \(\small y＝−x^2+2x+2\)を\(\small x\)軸方向に平行移動して点\(\small (2,1)\)を通るようにするためには、\(\small x\)軸方向にどのくらい平行移動すればよいか求めよ。
（3）放物線 \(\small y＝−x^2+3\)をどのように平行移動すると放物線 \(\small y=-x^2+6x-1\)になるか求めよ。
（4）放物線 \(\small y＝2x^2+kx+1\)を\(\small x\)軸方向に\(\small 1\)、\(\small y\)軸方向に\(\small -2\)だけ平行移動した放物線が点\(\small (0,-1)\)を通るとき、\(\small k\)の値を求めよ。

↓↓各問題の解説はこちら

問題（1）の解説
問題（2）,（3）の解説
問題（4）の解説

応用問題

（1）\(\small xy\)平面上の点の\(\small (-3,2)\)を通る2次関数 \(\small y＝f(x)\)がある。このグラフを\(\small x\)軸の正の方向へ\(\small 4\)だけ平行移動すると、\(\small x\)軸との交点が原点および点\(\small (2,0)\)となるような関数\(\small f(x)\)を求めよ。
（2）ある放物線を\(\small x\)軸方向に\(\small -1\)、\(\small y\)軸方向に\(\small -3\)だけ平行移動し、さらに\(\small x\)軸に関して対称移動すると放物線 \(\small y=x^2-2x+2\)となるとき、もとの放物線の方程式を求めよ。

↓↓各問題の解説はこちら

問題（1）の解説
問題（2）の解説

【基本問題1】平行移動前の方程式を求める問題

（1）\(\small x\)軸方向に\(\small -1\)、\(\small y\)軸方向に\(\small 2\)だけ平行移動すると放物線 \(\small y=x^2+3x+4\) に移されるような放物線の方程式を求めよ。

問題解決のKey

・平行移動前の方程式は、移動後の方程式を逆方向に平行移動すれば簡単に求まる！
・平行移動した式の求め方については、「【講義1】平行移動の公式」を参照。

　解説（1）

もとの放物線の方程式を求めたければ、『放物線 \(\small y=x^2+3x+4\)を\(\small x\)軸方向に\(\small 1\)、\(\small y\)軸方向に\(\small -2\)だけ平行移動』することで求めることができる。

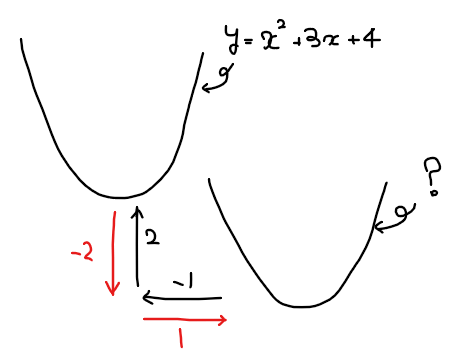
よって、移動後の式で\(\small x \to x-1\)、\(\small y \to y+2\)に置き換えてあげればよいので

\begin{split}
\small y+2 &\small =(x-1)^2+3(x-1)+4\\
\small \Leftrightarrow \space y+2 &\small=x^2-2x+1+3x-3+4\\
\small \Leftrightarrow \space \color{red}y &\small \color{red}{=x^2+x \space \cdots 【答】}\\
\end{split}

【基本問題2】どのように平行移動したか求める問題

（2）放物線 \(\small y＝−x^2+2x+2\)を\(\small x\)軸方向に平行移動して点\(\small (2,1)\)を通るようにするためには、\(\small x\)軸方向にどのくらい平行移動すればよいか求めよ。
（3）放物線 \(\small y＝−x^2+3\)をどのように平行移動すると放物線 \(\small y=-x^2+6x-1\)になるか求めよ。

問題解決のKey

平行移動の仕方の求め方
代表的な解法は以下の2通り。
・解法①：平行移動を文字でおき、移動後の方程式が満たす条件から文字を求める。
・解法②：移動前後の方程式が分かっている場合は、頂点の座標がどのくらい平行移動したかを確認する。

　解説（2）

放物線 \(\small y＝−x^2+2x+2\)を\(\small x\)軸方向に \(\small p\)だけ平行移動したとすると、移動後の放物線の方程式は \(\small x \to x-p\)と置き換えてあげればよいので、\(\small y= −\color{#ef5350}{(x-p)}^2+2\color{#ef5350}{(x-p)}+2\)となる。

この式が点\(\small (2,1)\)を通ればよいので、移動後の放物線の式に\(\small x=2,\) \(\small y=1\)を代入することで

\begin{split}
&\small \color{#ef5350}1 = −(\color{#ef5350}2-p)^2+2(\color{#ef5350}2-p)+2\\
\small \Leftrightarrow \space &\small 1=-(4-4p+p^2)+4-2p+2\\
\small \Leftrightarrow \space &\small p^2-2p-1=0\\
\small ∴ \space &\small \color{red}{p=1 \pm \sqrt{2} \space \cdots 【答】}\\
\end{split}

　解説（3）

（2）同様に\(\small x\)軸方向に\(\small p\)、\(\small y\)軸方向に\(\small q\)だけ平行移動したと文字でおいても解くことも可能だが、2次関数に代入して展開して係数比較した後に\(\small p\)と\(\small q\)の連立方程式を解く必要があり計算が大変…。

そこで本問では移動前後の放物線の方程式が分かっているので、頂点の座標がどの程度移動しているかを確認することでグラフがどの程度平行移動したのかを知ることができる。

移動前の放物線 \(\small y=-x^2+3\)の頂点の座標は、\(\small (0,3)\) …①.

移動後の放物線 \(\small y=-x^2+6x-1\)の頂点の座標は、

\begin{split}
\small y &\small =-(\color{#ef5350}{x^2-6x})-1\\
&\small =-\{\color{#ef5350}{(x-3)^2-9}\}-1\\
&\small =-(x-3)^2+8\\
\end{split}

よって、\(\small (3,8)\) …②.

①、②の座標のずれを確認すると\(\small x\)軸方向には\(\small 0 \to 3\)なので\(\small 3\)、\(\small y\)軸方向には\(\small 3 \to 8\)なので\(\small 5\)平行移動していることが分かる。

よって、\(\small x\)軸方向に3、\(\small y\)軸方向に5だけ平行移動すればよい …【答】.

【基本問題3】平行移動の条件を満たす定数を求める問題

（4）放物線 \(\small y＝2x^2+kx+1\)を\(\small x\)軸方向に\(\small 1\)、\(\small y\)軸方向に\(\small -2\)だけ平行移動した放物線が点\(\small (0,-1)\)を通るとき、\(\small k\)の値を求めよ。

問題解決のKey

（2）と同様に、移動後の放物線の式を求めてから通過する点の座標を代入することで\(\small k\)の値を求めることもできるが、移動後の放物線が通る点が\(\small (0,-1)\)と分かっているので、平行移動前は\(\small x\)軸方向に\(\small -1\)、\(\small y\)軸方向に\(\small 2\)だけ平行移動することで、点\(\small (-1,1)\)を通ることが分かるので、この座標を問題の放物線の式に代入する方が計算が楽である。

　解説（4）

平行移動後の放物線が点\(\small (0,-1)\)を通るということは、平行移動前の放物線は点\(\small (-1,1)\)を通ることから、\(\small x=-1\), \(\small y=1\)を問題の放物線の式に代入することで

\begin{split}
&\small 1=2\cdot (-1)^2+k\cdot(-1)+1\\
\small \Leftrightarrow \space &\small 1=2-k+1\\
\small ∴ &\small \quad \color{red}{k = 2 \space \cdots 【答】}\\
\end{split}

【別解】（2）同様の解法　
平行移動後の放物線の式は、\(\small x \to x-1\)、\(\small y \to y+2\)に置き換えてあげればよいので
\begin{split}
&\small \color{#ef5350}{y+2} =2 \color{#ef5350}{(x-1)}^2+k\color{#ef5350}{(x-1)}+1\\
\small \Leftrightarrow \space &\small y+2 =2(x^2-2x+1)+kx-k+1\\
\small \Leftrightarrow \space &\small y=2x^2+(k-4)x-k+1\\
\end{split}
上記の放物線が点\(\small (0,-1)\)を通ればよいので、\(\small x=0\), \(\small y=-1\)を代入することで
\begin{split}
&\small -1=2\cdot 0^2+(k-4)\cdot 0-k+1\\
\small \Leftrightarrow \space &\small -1=-k+1\\
\small ∴ &\small \quad \color{red}{k = 2 \space \cdots 【答】}\\
\end{split}

【応用問題1】平行移動前後の条件を満たす放物線を求める問題

問題解決のKey

平行移動前の2次関数を\(\small f(x)=ax^2+bx+c\)とおいて、点\(\small (-3,2)\)を通るという条件から
\begin{split}
&\small 2=9a-3b+c\\
\small \Leftrightarrow \space &\small c=-9a+3b+2\\
\end{split}
ゆえに、\(\small f(x)=ax^2+bx -9a+3b+2\)として、この式を平行移動した後に通過する点に着目して2次関数を決定してもよいが、計算がやや大変である。
『関数の平行移動』よりも『点の平行移動』の方が計算が簡単なことから、点\(\small (-3,2)\)を先に平行移動することで平行移動後に通過する3点から2次関数を決定してしまい、最後に平行移動前の2次関数を逆算する方が簡単だろう。

　解説（1）

平行移動後の関数を\(\small y = g(x)\)とする。

関数\(\small f(x)\)上の点 \(\small (-3,2)\)を\(\small x\)軸方向に4だけ平行移動すると点 \(\small (1,2)\)に移ることから、関数\(\small g(x)\)は点 \(\small (1,2)\)、点 \(\small (0,0)\)、点 \(\small (2,0)\)の3点を通る。

2点 \(\small (0,0)\)、\(\small (2,0)\)はいずれも\(\small x\)軸上の点なので関数\(\small g(x)\)は

\begin{split}
&\small g(x) = ax(x-2)\\
\end{split}

とおくことができる。これが点\(\small (1,2)\)を通ることから

\begin{split}
&\small 2 = a \cdot 1 \cdot (1-2)\\
\small ∴ \space &\small a=-2 \\
\end{split}

【補足】2次関数の決定
3点の座標が分かっている場合、一般には\(\small y = ax^2+bx+c\)とおいて3点の座標を代入した連立方程式を解くことで\(\small a,b,c\)の値を求めることができるが、今回は分かっている座標が特徴的な点なので、解答の方針で求めている。連立方程式で解いても同じ結果になる。

よって、\(\small g(x)=-2x(x-2)\)と求めることができたので、移動前の2次関数\(\small f(x)\)は\(\small x\)軸方向に\(\small -4\)だけ平行移動、すなわち \(\small x \to x+4\)に置き換えることで求めることができるので

\begin{split}
\small f(x) &\small=-2(x+4)\{(x+4)-2\}\\
&\small =-2(x+4)(x+2)\\
&\small =\color{red}{-2x^2-12x-16 \space \cdots 【答】}\\
\end{split}

【応用問題2】平行移動と対称移動の組合せ

（2）ある放物線を\(\small x\)軸方向に\(\small -1\)、\(\small y\)軸方向に\(\small -3\)だけ平行移動し、さらに\(\small x\)軸に関して対称移動すると放物線 \(\small y=x^2-2x+2\)となるとき、もとの放物線の方程式を求めよ。

問題解決のKey

・もとの放物線の式を求めるには、後ろから順に逆の手順で戻していく。
　☞ \(\small x\)軸に対称移動してから\(\small x\)軸方向に1、\(\small y\)軸方向に3だけ平行移動

　≫ 種々の移動　
・\(\small x\)軸に関して対称移動
　☞ \(\small y \to -y\)に置き換え　※\(\small y\)座標が反転
・\(\small y\)軸に関して対称移動
　☞ \(\small x \to -x\)に置き換え　※\(\small x\)座標が反転
・原点に関して対称移動
　☞ \(\small x \to -x\) かつ \(\small y \to -y\)に置き換え　※\(\small x,y\)座標が反転

　解説（2）

もとの放物線の式は、\(\small x\)軸に関して対称移動したあとに、\(\small x\)軸方向に1、\(\small y\)軸方向に3だけ平行移動することで求めることができる。

放物線 \(\small y=x^2-2x+2\)を\(\small x\)軸に関して対称移動した式は、\(\small y \to -y\)に置き換えればよいので

\begin{split}
&\small \color{#ef5350}{-y}=x^2-2x+2\\
\small \Leftrightarrow \space &\small y=-x^2+2x-2\\
\end{split}

この式を\(\small x\)軸方向に1、\(\small y\)軸方向に3だけ平行移動、すなわち、\(\small x \to x-1\)、\(\small y \to y-3\)に置き換えばよいので、

\begin{split}
&\small y-3=-(x-1)^2+2(x-1)-2\\
\small \Leftrightarrow \space &\small y-3=-(x^2-2x+1)+2x-2-2\\
\small ∴ \space &\small \color{red}{y=-x^2+4x-2 \space \cdots 【答】}\\
\end{split}

本記事のまとめ

今回は平行移動に関する問題について典型問題を一通り解説していきました。特に、平行移動のときに符号が感覚と逆方向になる理由についても解説してみました。

『\(\small x\)軸方向に\(\small p\)だけ移動した場合、関数の変数を\(\small x \to x-p\)に置き換えする』という結論自体は簡単なので暗記するで全然よいと思いますが、なぜそうなるのかを知っておくことが応用力を身に着ける近道だと思うので、数学で出てくるさまざまな定理や公式は余力があれば仕組みも併せて把握しておくのがおすすめです。導出方法や仕組みにまで踏み込んで理解しておくことが、逆に覚えることを減らすことに繋がったりします。

最後に本記事のポイントだけおさらいして終わりにしましょう。

☆重要ポイント☆
≫ \(\small x\)軸方向に\(\small p\)だけ平行移動したときに式の変数を\(\small x \to x-p\)に置き換える理由
⇒ 『変数の変更』＝『基準点の変更』なので、基準点がズレた分だけ変数自体は逆にズレるから。

では、今回は以上です。お疲れさまでした！