#PCやタブレットなどの大画面でご覧いただくと数式などが見やすいくなりおすすめです!
今回は、図形問題と極限値を求める問題の融合問題について解説していきます。図形+極限の問題は高校数学の様々な分野の知識と絡めた問題が作りやすく総合的な数学力を確認できることから大学入試でも頻出の分野になっていますが、それゆえどんな思考回路で解いていけばよいのか分かりにくいと悩む受験生も多いと思います。
そこで本記事では、図形問題に関する極限値を求める問題を通して解き方のコツを徹底解説していきます。極限の計算に自信がある人もない人も一緒に学んでいきましょう!
- 図形問題を題材とした極限値を求める問題に挑戦したい人
- 大学入試問題を通して極限分野の問題演習がしたい人
- 定期テスト対策がしたい人
【問題&解説】図形問題と極限値
【問題1】内分点に関する極限値(難易度:★★☆)
\(\small O\)を原点とする座標平面上に2点\(\small \mathrm{A}(2,0)、\mathrm{B}(0,1)\)がある。自然数\(\small n\)に対し、線分\(\small \mathrm{AB}\)を\(\small 1:n\)に内分する点を\(\small \mathrm{P}_n\)とし、\(\small \angle \mathrm{AOP}_n= \theta_n\)とする。ただし、\(\small \displaystyle 0<\theta_n<\frac{\pi}{2}\)である。
線分\(\small \mathrm{AP}_n\)の長さを\(\small \ell_n\)として、極限値 \(\small \displaystyle \lim_{n\to\infty} \frac{\ell_n}{\theta_n}\)を求めよ。
[福島県立医大]
・正弦定理や余弦定理を利用して平面図形的に解いてもよいが、座標平面の問題はベクトルを利用するのが得策!
まずは問題文の状況を図で整理しておく。
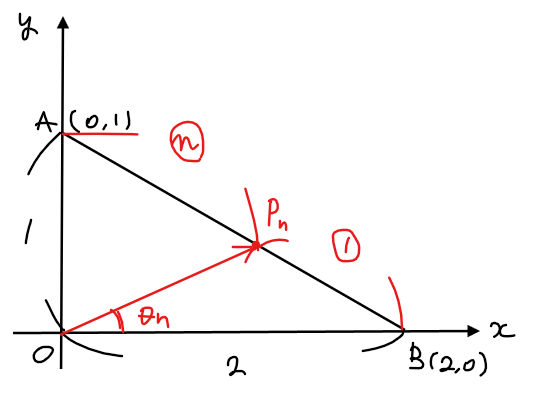
\(\small △\mathrm{OAB}\)において、内分点の公式[*1]から
\begin{split}
\small \overrightarrow{\mathrm{OP}_n} &\small = \displaystyle \frac{n\overrightarrow{\mathrm{OA}}+\overrightarrow{\mathrm{OB}}}{n+1}\\
&\small = \displaystyle \frac{n}{n+1}\overrightarrow{\mathrm{OA}}+\frac{1}{n+1}\overrightarrow{\mathrm{OB}}\\
&\small = \displaystyle \frac{n}{n+1}\left(2,0\right)+\frac{1}{n+1}\left(0,1\right)\\
&\small = \displaystyle \left(\dfrac{2n}{n+1},0\right)+\left(0,\dfrac{1}{n+1}\right)\\
&\small = \displaystyle \left(\dfrac{2n}{n+1}, \dfrac{1}{n+1}\right) \quad \cdots ①
\end{split}
*1:ベクトルの内分点の公式
△\(\small \mathrm{OAB}\)の辺\(\small \mathrm{AB}\)を\(\small m:n\)に内分する点\(\small \mathrm{P}\)は
$$\small \displaystyle \overrightarrow{\mathrm{OP}}=\frac{n\overrightarrow{\mathrm{OA}}+m\overrightarrow{\mathrm{OB}}}{m+n}$$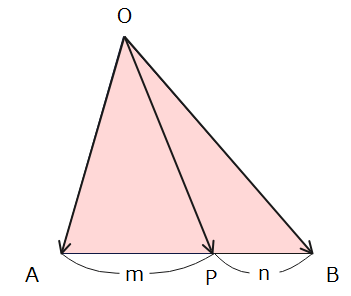
ここで、\(\small \sin \theta_n\)の値は、下図のように点\(\small \mathrm{P}_n\)から\(\small x\)軸に下した垂線の足を\(\small \mathrm{H}_n\)とすると
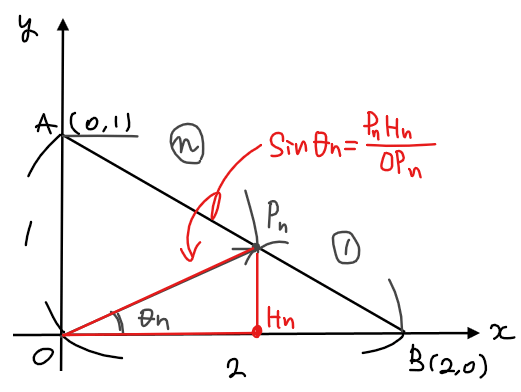
$$\small \displaystyle \sin \theta_n=\frac{\mathrm{P}_n\mathrm{H}_n}{\mathrm{OP}_n}$$
と表せる。
線分 \(\small \mathrm{OP}_n\)の長さは①より、
\begin{split}
\small |\overrightarrow{\mathrm{OP}_n} |^2=&\small \displaystyle \left(\dfrac{2n}{n+1}\right)^2+\left(\dfrac{1}{n+1}\right)^2\\
\small =&\small \displaystyle \dfrac{4n^2+1}{(n+1)^2}\\
\small ∴ \space |\overrightarrow{\mathrm{OP}_n} |=&\small \displaystyle \dfrac{\sqrt{4n^2+1}}{n+1}\\
\end{split}
また、線分 \(\small \mathrm{P}_n\mathrm{H}_n\)の長さは点\(\small \mathrm{P}_n\)の \(\small y\)座標、すなわち\(\small \overrightarrow{\mathrm{OP}_n}\)の \(\small y\)座標 [*2]なので、
\begin{split}
\small \mathrm{P}_n\mathrm{H}_n =&\small \displaystyle \dfrac{1}{n+1}\\
\end{split}
*2:補足
原点を始点とするベクトルの成分表示は、終点の座標になります。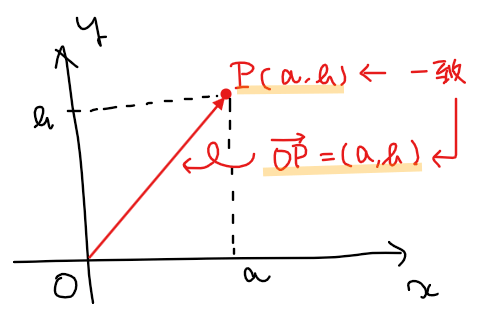
ゆえに、
\begin{split}
\small \displaystyle \sin \theta_n &\small \displaystyle =\frac{1}{\sqrt{4n^2+1}} \quad \cdots ②\\
\end{split}
また、
\begin{split}
\small \displaystyle \ell_n &\small \displaystyle =\frac{1}{n+1}\mathrm{AB}\\
&\small \displaystyle =\frac{\sqrt{5}}{n+1} \quad \cdots ③\\
\end{split}
②、③より、求める極限は
\begin{split}
\small \displaystyle \lim_{n\to\infty} \frac{\ell_n}{\theta_n} &\small \displaystyle =\lim_{n\to\infty} \frac{\sin \theta_n}{\theta_n} \times \frac{\ell_n}{\sin \theta_n} \\
&\small \displaystyle =\lim_{n\to\infty} 1 \cdot \frac{\sqrt{5}\sqrt{4n^2+1}}{n+1} \quad [*3]\\
&\small \displaystyle =\lim_{n\to\infty}\frac{\sqrt{5}\sqrt{4+\dfrac{1}{n^2}}}{1+\dfrac{1}{n}} \\
&\small =\color{red}{2\sqrt{5}\space \cdots 【答】}
\end{split}
*3:補足
\(\small n \to \infty\)の極限では、イメージとして線分\(\small \mathrm{AB}\)が\(\small 1:\infty\)に内分される=点\(\small \mathrm{P}_n\)が点\(\small \mathrm{B}\)に限りなく近づくことになる。つまり、\(\small \theta_n \to 0\)になることから、
\begin{split}
&\small \displaystyle \lim_{n\to\infty} \frac{\sin \theta_n}{\theta_n} \\
\small =&\small \lim_{\theta_n\to 0} \frac{\sin \theta_n}{\theta_n}\\
\small =&\small 1\\
\end{split}
・角度を含む極限値の計算は、\(\small \sin \theta /\theta \)の形に変形しよう。
【問題2】面積の極限値(難易度:★☆☆)
#はじめに…
本問題は数Ⅲの積分の知識が必要になるのであらかじめご了承くださいm(__)m
\(\small \displaystyle 0 < t < \frac{\pi}{2}\)とする。曲線 \(\small y=\sin x\)上の点 \(\small \displaystyle \mathrm{P}\left(t+\frac{\pi}{2},\sin\left(t+\frac{\pi}{2}\right)\right)\)における法線を\(\small \ell\)、直線 \(\small \displaystyle x=\frac{\pi}{2}\)を\(\small m\)とおき、法線 \(\small \ell\)と直線 \(\small m\)の交点を\(\small \mathrm{Q}\)とおく。曲線 \(\small y=\sin x\)と法線 \(\small \ell\)および直線 \(\small m\)で囲まれた部分の面積を\(\small S(t)\)とするとき、\(\small \displaystyle \lim_{t\to +0}\frac{S(t)}{t}\)を求めよ。 [2014年北里大 改題]
極限の分母にある\(\small S(t)\)を求めることができればあとはただの極限計算の問題に帰着できるので、\(\small S(t)\)を求める方針で計算していけばよいだろう。
点\(\small \mathrm{P}\)の\(\small x\)座標である\(\small \displaystyle t+\frac{\pi}{2}\)が
\begin{split}
&\small 0 < t <\frac{\pi}{2}\\
\small \Leftrightarrow \space &\small \color{#ef5350}{0 < t+\frac{\pi}{2} <\pi}\\
\end{split}
の範囲にあることから、問題文の状況を図示すると以下のようになる。
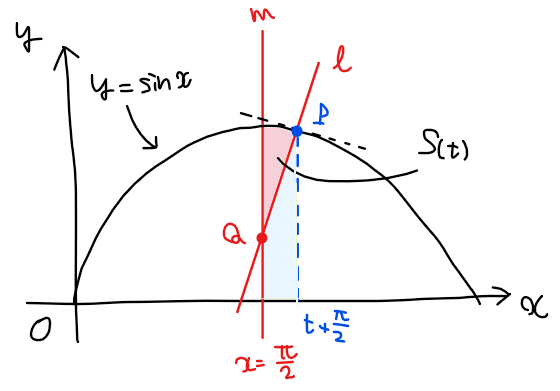
上図から、\(\small S(t)\)は
\begin{split}
\small S(t) &\small \displaystyle = \int_{\frac{\pi}{2}}^{t+\frac{\pi}{2}} \sin x dx -\color{blue}{\mathsf{青色部分の台形の面積}}\\
&\small \displaystyle = \bigg[-\cos x \bigg]_{\frac{\pi}{2}}^{t+\frac{\pi}{2}} -\color{blue}{\mathsf{青色部分の台形の面積}}\\
&\small \displaystyle = \sin t -\color{blue}{\mathsf{青色部分の台形の面積}}\quad \cdots (*)\\
\end{split}
と表せる。青色部分の台形の面積は、点\(\small \mathrm{P}\)と点\(\small \mathrm{Q}\)の\(\small y\) 座標が分かれば計算できることから、これらの座標を求めていこう。
まず点\(\small \mathrm{P}\)は\(\small x\)座標が\(\small \displaystyle t+\frac{\pi}{2}\)と分かっていることから、\(\small y\)座標は、
\begin{split}
\small \displaystyle \sin \left( t+\frac{\pi}{2}\right)=\cos t
\end{split}
と求められる。よって、
\begin{split}
\small \displaystyle \color{#ef5350}{\mathrm{P}\left( t+\frac{\pi}{2},\cos t\right) \quad \cdots ①}
\end{split}
点\(\small \mathrm{P}\)における接線の傾きは、\(\small y’=\cos x\)より、
\begin{split}
\small \displaystyle(\mathsf{点}\mathrm{P}\mathsf{の接線の傾き})&\small \displaystyle =\cos \left(t+\frac{\pi}{2}\right)\\
&\small =-\sin t\\
\end{split}
なので、法線 \(\small \ell\)の傾きは\(\small \displaystyle \frac{1}{\sin t}\)。
●補足
2直線\(\small y=mx+a\)と\(\small y=nx+b\)が直交(直角に交わる)する条件は
$$\small mn=-1$$
法線とは接線に直交する直線のことなので、この性質を利用することで接線の傾きから法線の傾きを求めることができる。
また、法線 \(\small \ell\)は\(\small \displaystyle \mathrm{P}\left( t+\frac{\pi}{2},\cos t\right)\) を通ることから、直線の方程式は
\begin{split}
\small \displaystyle \ell : y=\frac{1}{\sin t}\left\{ x-\left( t+\frac{\pi}{2} \right) \right\}+\cos t\\
\end{split}
点\(\small \mathrm{Q}\)がこの法線 \(\small \ell \)上の点かつ\(\small x\)座標が\(\small \displaystyle \frac{\pi}{2}\)であることから、\(\small y\) 座標は
\begin{split}
\small \displaystyle \ell : y & \small =\frac{1}{\sin t}\left\{ \color{red}{\frac{\pi}{2}}-\left( t+\frac{\pi}{2} \right) \right\}+\cos t\\
& \small =-\frac{t}{\sin t}+\cos t\\
\end{split}
よって、
\begin{split}
\small \displaystyle \color{#ef5350}{\mathrm{Q}\left(\frac{\pi}{2},-\frac{t}{\sin t}+\cos t\right) \quad \cdots ②}
\end{split}
であり、\(\small \displaystyle 0 < t <\frac{\pi}{2}\)の範囲では\(\small \sin t >0、\cos t>0\)であることから、点\(\small \mathrm{Q}\)の\(\small y\)座標は常に正である。
●補足
\(\small t\)の値によって、点\(\small \mathrm{Q}\)の\(\small y\)座標が負になる場合、冒頭の\(\small S(t)\)の面積を求める際に出てきた青色部分が台形ではなくなるため、場合分けが必要になるので、その必要がないかを確認している。
①、②より、青色部分の台形の面積は、
\begin{split}
\small \displaystyle (青色部分の台形の面積)&\small =\frac{1}{2}t \left[(点\mathrm{P}のy座標)+(点\mathrm{Q}のy座標) \right]\\
&\small =\frac{1}{2}t \left( \cos t-\frac{t}{\sin t}+\cos t\right)\\
&\small =t\cos t-\frac{t^2}{2\sin t}\space \cdots ③\\
\end{split}
\(\small (*)\)に③を代入することで
\begin{split}
\small S(t) &\small \displaystyle = \sin t-t\cos t+\frac{t^2}{2\sin t}\\
\end{split}
よって、求める極限は
\begin{split}
\small \lim_{t\to+0} \frac{S(t)}{t} &\small \displaystyle = \lim_{t\to+0} \left(\frac{\sin t}{t}-\cos t+\frac{t}{2\sin t}\right)\\
&\small \displaystyle = 1-1+\frac{1}{2}\\
&\small \displaystyle = \color{red}{\frac{1}{2}\space \cdots 【答】}\\
\end{split}
●補足
極限の第3項目は、
\begin{split}
&\small \lim_{t\to+0} \frac{t}{2\sin t}\\
&\small \displaystyle =\frac{1}{2\lim\limits_{t\to+0} \dfrac{\sin t}{t}}\\
&\small \displaystyle =\frac{1}{2}\\
\end{split}
【問題3】面積の極限値(2)(難易度:★★★)
\(\small n\)を3以上の自然数とする。点\(\small \mathrm{O}\)を中心とする半径1の円において、円周を\(\small n\)等分する点\(\small \mathrm{P}_0,\mathrm{P}_1,\cdots,\mathrm{P}_{n-1}\)を時計回りにとる。各\(\small i=1,2,\cdots,n\)に対して、直線\(\small \mathrm{OP}_{i-1},\mathrm{OP}_i\)とそれぞれ点\(\small \mathrm{P}_{i-1},\mathrm{P}_i\)で接するような放物線を\(\small C_{i}\)とする。ただし、\(\small \mathrm{P}_n\)と\(\small \mathrm{P}_0\)は一致する。放物線\(\small C_1,C_2,\cdots,C_n\)によって囲まれる部分の面積を\(\small S_n\)とするとき、\(\small \lim\limits_{n\to\infty}S_n\)を求めよ。 [大阪大]
・円上の点の座標を表す際には、安直に\(\small (x,y)\)とおくのではなく角度を利用すると使用する文字を減らし計算式が複雑になるのを防ぐことができる。
点\(\small \small \mathrm{P}_0,\mathrm{P}_1,\cdots,\mathrm{P}_{n-1}\)の基準点はどこに設定しても求める\(\small S_n\)は変わらないため、本解答では下図のように\(\small \mathrm{P}_0\)と\(\small \mathrm{P}_1\)が\(\small y\)軸対称になるように設定する。
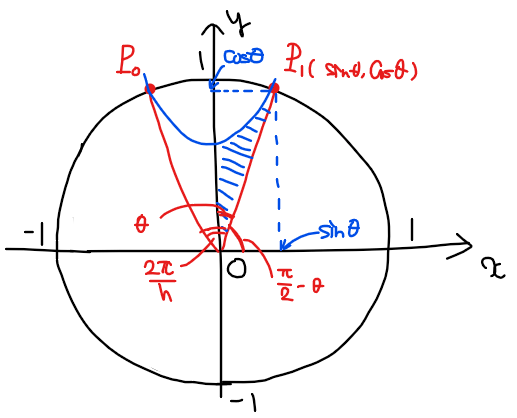
点\(\small \mathrm{P}_1\)と\(\small y\)軸のなす角度を\(\small \theta\)とおくと、点\(\small \mathrm{P}_i\)が円周を\(\small n\)等分する点の集合であることから、\(\small \displaystyle \angle \mathrm{P}_0\mathrm{OP}_1=\frac{2\pi}{n}\)より、\(\small \displaystyle \theta =\frac{\pi}{n}\)となる。
また、点\(\small \mathrm{P}_1\)の座標は
\begin{split}
\small \displaystyle \mathrm{P}_1\left( \sin \theta,\cos \theta \right)\\
\end{split}
●補足
通常単位円などでよく設定しているように\(\small x\)軸とのなす角度を\(\small \theta\)とする設定とは異なり、今回の\(\small \theta\)は\(\small y\)軸との角度である点に注意する。
\begin{split}
&\small \displaystyle \mathrm{P}_1\left( \cos\left(\frac{\pi}{2}-\theta\right),\sin\left(\frac{\pi}{2}-\theta\right)\right)\\
\small ∴\space &\small \displaystyle \mathrm{P}_1\left( \sin \theta,\cos \theta \right)\\
\end{split}
\(\small C_1\)の放物線の式を\(\small C_1:f(x)=ax^2+b\)とすると、点\(\small \mathrm{P}_1\)を通ることから、
\begin{split}
&\small \displaystyle \cos \theta =a \sin^2 \theta +b\space \cdots ①
\end{split}
また、点\(\small \mathrm{P}_1\)が放物線\(\small C_1\)の接点となっており、そのときの接線の傾きは、
\begin{split}
&\small f^\prime(\sin\theta)=2ax|_{x=\sin \theta}=2a\sin\theta\\
\end{split}
であり、これが直線\(\small \mathrm{OP}_1\)の傾きと一致することから、
\begin{split}
&\small \displaystyle 2a\sin\theta=\frac{\cos\theta}{\sin\theta}\\
\small \Leftrightarrow \space &\small \displaystyle a=\frac{\cos\theta}{2\sin^2\theta}\\
\end{split}
この結果を①に代入することで、
\begin{split}
&\small \displaystyle b=\frac{\cos\theta}{2}
\end{split}
よって、放物線\(\small C_1\)は、\(\small \displaystyle C_1:f(x)=\frac{\cos\theta}{2\sin^2\theta}x^2+\frac{\cos\theta}{2}\)と求まる。
今回求める面積\(\small S_n\)は、下図の青色部分の面積の\(\small 2n\)倍(\(\small n\)等分の1をさらに半分にしているので)なので、青色部分の面積を求めることを考える。
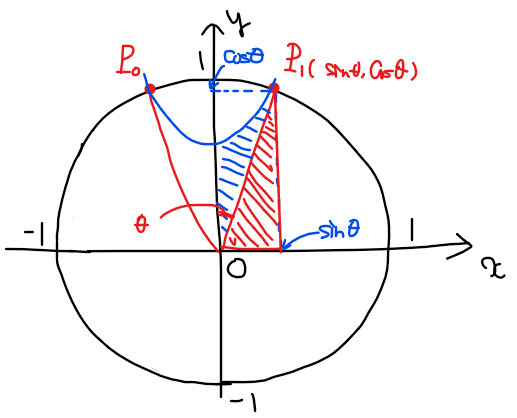
青色部分の面積は、\(\small C_1\)と直線\(\small x=0\)、直線\(\small x=\sin\theta\)で囲まれた面積(\(\small S_1\)とする)から赤色部分の三角形の面積(\(\small S_2\)とする)を引き算すればよい。
\begin{split}
\small S_1 &\small \displaystyle =\int_0^{\sin\theta}\left(\frac{\cos\theta}{2\sin^2\theta}x^2+\frac{\cos\theta}{2}\right) dx\\
&\small \displaystyle =\left[\frac{\cos\theta}{2\sin^2\theta}\frac{x^3}{3}+\frac{\cos\theta}{2}x \right]_0^{\sin\theta}\\
&\small \displaystyle =\frac{1}{6}\sin\theta\cos\theta+\frac{1}{2}\sin\theta \cos\theta\\
&\small \displaystyle =\frac{2}{3}\sin\theta\cos\theta\\
\end{split}
\begin{split}
\small S_2 &\small \displaystyle =\frac{1}{2}\sin\theta \cos\theta\\
\end{split}
よって、青色部分の面積は、
\begin{split}
\small S_1-S_2 &\small \displaystyle =\frac{1}{6}\sin\theta \cos\theta\\
\end{split}
青色部分の面積を\(\small 2n\)倍したものが今回求める面積\(\small S_n\)なので、
\begin{split}
\small S_n &\small \displaystyle =2n \times \frac{1}{6}\sin\theta \cos\theta\\
&\small \displaystyle =\frac{n}{3}\sin\theta \cos\theta\\
\end{split}
ここで、\(\small \displaystyle \theta =\frac{\pi}{n}\)と設定していたことから、求める極限は
\begin{split}
\small \lim_{n\to\infty} S_n &\small \displaystyle =\lim_{n\to\infty} \frac{n}{3}\sin\left(\frac{\pi}{n}\right) \cos\left(\frac{\pi}{n}\right)\\
&\small \displaystyle =\lim_{n\to\infty} \frac{n}{3}\frac{\sin\left(\dfrac{\pi}{n}\right)}{\color{red}{\dfrac{\pi}{n}}} \times \color{red}{\frac{\pi}{n}}\times \cos\left(\frac{\pi}{n}\right)\\
&\small \displaystyle =\frac{\pi}{3} \lim_{n\to\infty} \left[\frac{\sin\left(\dfrac{\pi}{n}\right)}{\dfrac{\pi}{n}}\right]\cos\left(\frac{\pi}{n}\right)\\
&\small \displaystyle =\color{red}{\frac{\pi}{3} \space \cdots 【答】}\\
\end{split}
本記事のまとめ
今回は図形問題と絡めた極限値を求める問題について解説していきましたがいかがでしたか?図形問題では三角関数がほぼほぼ出てくるので、三角関数の極限の代表的な公式である\(\small \displaystyle \lim_{x \to 0}\frac{\sin x}{x}=1\)は絶対に覚えておきましょう。
最後に、図形問題の極限で頻出の公式について、注意したいと危ない罠とその回避策として正確に公式を覚えるためのコツを確認して終わりにしたいと思います。
【図形の極限で頻出】\(\small \sin x/x\)公式の罠と覚え方
ちなみに、この公式とよく似た形で\(\small \displaystyle \lim_{x\to \infty}\frac{\sin x}{x}\)がありますが、この場合は極限値は0になります(解説は後述)。サインの角度部分の極限が「0」なのか「∞」なのかが非常に重要になるわけですね。
この話を聞くと、どっちのときが1になるのか忘れそう…と不安になりそうですが、個人的におすすめの覚え方があります。それは、図形的な意味で理解する覚え方です。
どういう言うことか説明すると、\(\small \displaystyle \lim_{x\to 0}\frac{\sin x}{x}=1\)の公式は、\(\small x\)が0付近で\(\small \displaystyle \frac{\sin x}{x}=1\)が成り立つ、すなわち\(\small \sin x =x\)が成り立つということを言ってます。\(\small \sin x =x\)が成り立つということは、関数\(\small y=\sin x\)と\(\small y=x\)が\(\small x\to0\)のときにグラフ的に重なるという意味合いになるワケですが、実際にグラフをイメージすると確かに重なってそうですね(下図)。
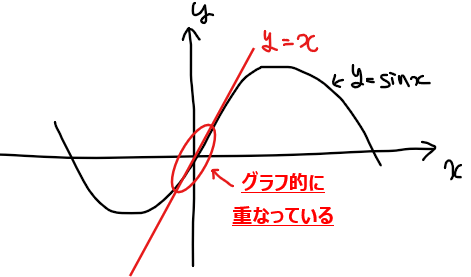
なので、\(\small \lim_{x\to 0}\sin x/x\)の極限値を忘れてしまった場合は、\(\small y=\sin x\)と\(\small y=x\)のグラフをイメージして\(\small x \to 0\)だから原点付近ではグラフが重なっている(=同じ)ということは1になるなと確認できるとよいでしょう。
同じ考え方で冒頭に触れた\(\small \displaystyle \lim_{x \to \infty}\frac{\sin x}{x}\)の極限値も考えることができます。今度は\(\small x \to \infty\)なので、グラフの右側をイメージします。すると分母は\(\small y=x\)と無限に大きな数になることが分かります。一方で、分子の\(\small y=\sin x\)は周期関数なので、\(\small -1~1\)の間をうろついているだけです。よって、分母の値が非常に大きくなるので、全体としては0に収束することが分かります。
●補足
しっかりとした証明をする場合は、\(\small |\sin x|≦1\)であることを用いて、はさみうちの原理を利用すれば示すことができますが、ここでは割愛します。気になる人は実際に計算してみましょう。
では、今回はここまでです。お疲れさまでした!








コメント