【整数問題】n乗を含む不定方程式の整数解【有名大学入試の良問】【合同式】（千葉大、東北大、九州大）

今回は、整数問題の中でも難問と言われる問題が多い「n乗を含む整数解の求め方」について徹底解説していきます。一番とっかかりずらい分野であり「何から手を付けていいのか分からない…」という人向けに実際の入試問題を題材に解き方のコツを分かりやすく解説しているので、ぜひ最後まで読んでみてください！

• 以下のような不定方程式の問題が苦手…
  \(\small \color{red}{3^n=k^3+1}\)を満たす正の整数組\(\small (k,n)\)を全て求めよ
  \(\small \color{red}{3^a-2^b=1}\)を満たす整数解\(\small (a,b)\)の組をすべて求めよ
• 解説を読んだら理解できるけどどうやったら自分で解法を導き出せるのか知りたい！
• 問題を解いて自分の実力をチェックしたい！

【解説編】\(\small n\)乗を含む不定方程式の解き方

この記事でいう「\(\small n\)乗を含む不定方程式」というのは\(\small 2^n=\cdots\) のように指数の部分に文字が来ている不定方程式のことを指すことにします。なので、\(\small n\)乗でなくても、\(\small a\)乗や\(\small p\)乗でもよいです。とにかく指数の部分が文字になっている整数問題をイメージしてもらえればOKです！

合同式を利用しろ

苦手な人が多い\(\small n\)乗（指数型）の不定方程式ですが、整数解の求め方の基本方針はすごくシンプルです。基本方針を一言でいうと「合同式を利用せよ」、以上です。キーワードは「合同式」になります。これだけは絶対に覚えておきましょう。

「合同式ってなんだっけ？(ﾟДﾟ;)」という人向けに簡単に復習しておきましょう。

■合同式とは
　余りに着目した方程式。
　例：\(\small \color{red}{10} \equiv \color{blue}1 \pmod{\color{green}3}\)
　　　→「\(\small \color{red}{10}\)を\(\small \color{green}3\)で割った余りは\(\small \color{blue}1\)」という意味
　　　　（mod 3は3で割った余りの世界で考えようということだった）

合同式を利用した解き方のポイント

「でも、合同式を使えって言われてもどう使えばいいの？(-_-;)」となると思うので、合同式の代表的な使い方と合同式を使った解き方のポイントについて紹介します。

STEP1の合同式を方程式のようにして解くという部分について次章で具体的に説明します。

【絶対に覚えろ！】合同式の重要な性質

ここでは整数問題で頻出の合同式の計算方法について例題で解説します。これは絶対に覚えてください！

この式変形のやり方が整数問題では頻出なので、しっかり覚えましょう。

両辺のmod2を考えると

\begin{split}
\color{red}3\cdot \color{blue}5^n&= \color{green}k+\color{darkorange}2\\
\Rightarrow \space \color{red}1\cdot \color{blue}{1^n} &\equiv \color{green}k+\color{darkorange}0\pmod{2}\\
k &\equiv 1\pmod{2} \quad \cdots \mathbf{(答)}
\end{split}

実際の整数問題では、上記の式から、\(\small k\)は2で割ったら1余る数であることを表しているので、\(\small \color{red}{k=2\ell+1}\)とおいて解の条件を絞ることになる。

（補足）式それぞれのmodを考えればいい理由
合同式の計算に慣れていないと、\(\small 3\cdot 5^n\)のmod2を計算しようと思っても「n乗があるし、3倍もされているしよくわからん…」というmod2の定義から考えだしてしまい手が止まるだろう。でも、この計算自体は簡単で解答で書いた通り、それぞれ単品でmod2の計算結果に置き換えてあげればよい。
この計算でよい理由は、以下ポイントにある「合同式の性質」の①～③の性質を組み合わせて考えると理解できる。

\begin{split}
3 &\equiv 1 \pmod{2}\cdots(a)\\
5 &\equiv 1 \pmod{2}\\
→& \space 5^n \equiv 1^n \pmod{2}\cdots(b) \space (∵\mathbf{「}③\small \mathrm{-1}\mathbf{」の性質を}n\mathbf{回繰り返し適用})\\
k &\equiv k \pmod{2}\cdots(c)\\
2 &\equiv 0 \pmod{2}\cdots(d)\\
\end{split}
③-1の性質で(a)と(b)を掛け合わせると、\(\small 3\cdot5^n \equiv 1\cdot 1^n \pmod{2}\cdots(e)\)。
一方で、①の性質で(c)と(d)を足し合わせると、\(\small k+2 \equiv k+0 \pmod{2}\cdots(f)\)。
問題文より、(e)と(f)の左辺はイコールなので、\(\small 1\cdot1^n\equiv k+0 \pmod{2}\)。
というわけで、毎回この計算をするのは大変なので、結論、それぞれ単品でmod2に置き換えてあげればよいという変形方法を覚えておこう。

【問題＆解説】\(\small n\)乗を含む不定方程式の整数解

【問題1】\(\small n\)乗を含む不定方程式の整数解[千葉大]

右辺の\(\small k^3+1^3\)を見ると、\(\small x^3+y^3=k\)型の不定方程式として解きたくなるが、\(\small (k+1)(k^2-k+1)=3^n\)と因数分解して

\begin{cases}
k+1&=3^a\\
k^2-k+1=&3^{n-a}\\
\end{cases}

として\(\small 3^{n-a}=3^{2n}-3k\)まで式変形できるが、n乗の処理ができずに行き詰ってしまう。n乗を処理するためには合同式で余りが満たすべき条件から解の候補を絞っていくのが有効である。

両辺のmod3（3で割った余り）を考える。\(\small 3^n\)を3で割ると余りが0、1を3で割ると余りが1は自明だが、\(\small k^3\)を3で割った余りはすぐには分からないので、\(\small k^3\)のままとして方程式を解くと

\begin{split}
3^n&=k^3+1\\
\Rightarrow\space 0 &\equiv k^3+1 \pmod{3}\\
\Rightarrow\space k^3&\equiv -1 \pmod{3}\\
\Rightarrow\space k&\equiv \color{red}{-1} \pmod{3}\quad \cdots (*)\\
\end{split}

\(\small k\)は整数なので方程式の解は\(\small -1\)だけになります。

よって、式\(\small (*)\)が表す意味を言語化すると、「\(\small k\)は3で割ったときに-1余る数」ということになるので、一般的に

$$k=3\ell-1\space (\ell =1、2、\cdots)$$
と表すことができます。

（補足）マイナスの余りってなに？
通常余りはプラスだが、マイナスの余りという概念を取り入れると計算が楽になることがある。たとえば、整数\(\small n\)が4で割って3余る数だとすると、\(\small n=4\ell\color{red}{+3}\)（\(\small \ell\)は整数）として\(\small n \equiv \color{red}3 \pmod{4}\)としてもよいが、\(\small n=4\ell\color{blue}{-1}\)（\(\small \ell\)は整数）として\(\small n \equiv \color{blue}{-1} \pmod{4}\)と表すこともできる。
\begin{cases}
n&=4\ell+3=\cdots、3、7、10、13、\cdots\\
n&=4\ell-1=\cdots、-1、3、7、10、\cdots\\
\end{cases}
特に余りを\(\small -1\)で表すテクニックは整数問題では頻出なので覚えておきましょう。

（補足）すべての整数は余りの種類数で分類できる
例えば、ある整数を3で割ったときの余りは、0、1、2の3パターン（実際に適当な数を選んで3で割ると3パターンしかないことが確認できる）で、それぞれ、\(\small 3\ell、3\ell+1、3\ell+2\)（\(\small \ell\)は整数）と表せる。
一般に整数を\(\small n\)で割ったときの余りは\(\small n\)パターンあるので、余りの種類によって\(\small n\)種類に分類できる。難しく聞こえるが、2で割ったときの余りのパターンは、0か1の2種類で、余りが0（2で割り切れる）の数を偶数、余りが1の数を奇数と分類するという考え方はその代表例である。

合同式を利用して解の形が絞れたので、この結果を問題の式に代入して因数分解の形に持って行く。

\begin{split}
3^n&=k^3+1\\
3^n&=(3\ell -1)^3+1^3\\
3^n&=\{(3\ell -1)+1\}\{(3\ell -1)^2-(3\ell -1)+1\}\\
3^n&=3\ell (9\ell^2-9\ell+3)\\
3^n&=9\ell (3\ell^2-3\ell+1)\\
\end{split}

左辺は\(\small 3^n=3\times3\times\cdots\times3\)のように3が\(\small n\)回掛け算された式なので右辺も同じように3のかけ算になっている必要があるので、

\begin{cases}
\ell = 3^p\quad \cdots ①\\
3\ell^2-3\ell+1 = 3^q\quad \cdots ②\\
\end{cases}

①を②に代入すると

\begin{split}
3\cdot3^p(3^p-1)+1 = 3^q
\end{split}

上式は左辺が3の倍数+1、右辺が3の倍数なので一見成立しないように思えるが、両辺が1のときだけ成立することができ、\(\small p=0、q=0\)となる。

よって、①より

\begin{split}
\ell&=3^q=3^0=\color{red}1\\
k&=3\ell-1\\
&=3\cdot \color{red}1-1\\
\mathbf{∴} \space k& =\color{blue}2\\
3^n&=k^3+1\\
&=\color{blue}2^3+1\\
&=9\\
&=3^{\color{green}2}\\
\mathbf{∴} \space n& =2\\
\end{split}

（解答）
\(\small \quad \color{red}{(k,n)=(2,2)}\)

【問題2】\(\small n\)乗を含む不定方程式の整数解[一橋大]

\(\small n\)乗があるので合同式で解の条件を絞り込む。\(\small n^n+1\)が3で割り切れるためには

\begin{split}
n^n +& 1 \equiv 0 \pmod{3}\\
n^n &\equiv -1 \pmod{3}\\
\end{split}

を満たす必要があるので、\(\small n^n\)は3の倍数-1の数、すなわち、\(\small \color{red}{n^n=3k-1 \cdots①}\)（\(\small k=1、2、3、\cdots\)）とおける。ここから、\(\small n\)が満たすべき条件をmod3のパターンで場合分けして考える。

[1] \(\small n \equiv 0 \pmod{3}\)の場合
\(\small n^n \equiv 0^n=0 \pmod{3}\)なので
\begin{split}
n^n&=3k-1\\
\Rightarrow \space 0 &\equiv 0-1 \pmod{3}\\
0 &\equiv -1 \pmod{3}\rightarrow \space \color{red}{×\mathbf{不適}}\\
\end{split}

[2] \(\small n \equiv 1 \pmod{3}\)の場合
\(\small n^n \equiv 1^n=1 \pmod{3}\)なので
\begin{split}
n^n&=3k-1\\
\Rightarrow \space 1 &\equiv -1 \pmod{3} \rightarrow \space \color{red}{×\mathbf{不適}}\\
\end{split}

[3] \(\small n \equiv -1 \pmod{3}\)の場合
\(\small n^n \equiv (-1)^n \pmod{3}\)なので
\begin{split}
n^n&=3k-1\\
\Rightarrow \space (-1)^n &\equiv -1 \pmod{3}\\
\end{split}
上式が成り立つには、\(\small n\)が奇数であればよい。一方で、そもそも\(\small n \equiv -1 \pmod{3}\)なので、\(\small n=3m-1\)（\(\small m=1、2、3、\cdots\)）と表せるので、これが奇数になるには\(\small 3m\)が偶数、すなわち\(\small m=2\ell\)（\(\small \ell =1、2、3、\cdots\)）と表せる必要があるので、

\begin{split}
\color{red}{n=}3\cdot(2\ell)-1=\color{red}{6\ell-1\space (\ell=1、2、3、\cdots)}
\end{split}

あとは、100以下で上記を満たす\(\small \ell\)の個数を調べればよいので（\(\small \ell\)が決まると\(\small n=6\ell-1\)に代入することで\(\small n\)も決まるため）

\begin{split}
n=6\ell-1&≦100\\
6\ell&≦101\\
\ell&≦\frac{101}{6}=16.8\cdots\\
\end{split}

よって、\(\small \ell\)は1～16までの\(\small \color{red}{16}\)個…(答)

【問題3】\(\small n\)乗を含む不定方程式の整数解[東北大]

●注意
この問題は一部数学Ⅱの知識が必要です。

\(\small 2^b>0\)であることから、\(\small 3^a=2^b+1>\color{red}0+1=1\)より、\(\small \color{red}{a>0}\)。

（補足）指数の性質【数学Ⅱ】
#指数がマイナスになったり、分数になるパターンは数学Ⅱの「指数関数」で詳しく学習するので未学習の人は参考程度に…
\(\small 3^a>1\)ならば\(\small a>0\)になる理由については、指数関数のグラフをイメージするとわかりやすいと思います。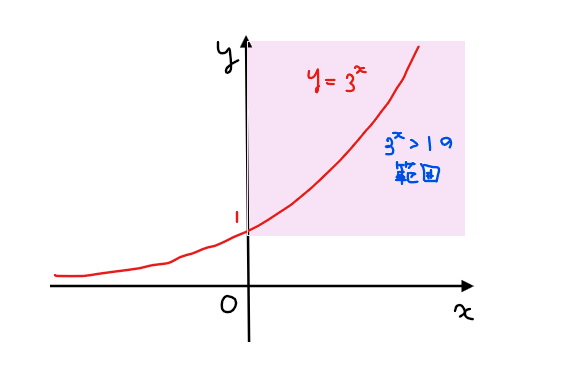

上記のグラフを見ると、\(\small 3^x>1\)である紫色の範囲では必ず\(\small x>0\)となっていることが分かります。（逆に\(\small 3^x<1\)の範囲では\(\small x<0\)になっている）
数式的にも考えてみます。まず、\(\small a≧1\)(たとえば\(\small a=1、2、3、\cdots\)をイメージしてください)の場合、\(\small 3^a\)は3以上の数字になるので明らかに1より大きくなります。
次に\(\small a<0\)の場合、\(\small 3^a\)は\(\small \displaystyle \frac{1}{3}、\frac{1}{9}、\cdots\)など1より小さい数になります。
最後に\(\small 0<a<1\)の場合が少しイメージしにくいですが、\(\small a\)の値が大きくなるほど、\(\small 3^a\)も大きくなることから、指数の大小関係が\(\small 3^a\)自体の大小関係になります。つまり、\(\small 1<3^a<3\)（\(\small 3^{\color{red}0}<3^{\color{red}a}<3^{\color{red}1}\)）となるので1より小さい数になります。

\(\small a\)は\(\small a>0\)を満たす整数なので\(\small a≧1\)としても問題ない。\(\small 2^b=3^a-1≧3^1-1=2\)より、\(\small 2^b≧2\)なので\(\small \color{red}{b≧1}\)。よって題意は示された。

（補足）\(\small a、b\)が0や負だと①式が成り立たないことを示す方針はだめ？
結論、たくさんの場合分けが必要なので逆に面倒くさくなります。この問題では、\(\small a、b\)がともに正であることを示さないとだめなので、成り立たない場合のパターンとしては
　①\(\small a>0、b≦0\)
　②\(\small a≦0、b>0\)
　③\(\small a≦0、b≦0\)
となり、それぞれを示す方が大変そう…。余事象的な考え方は考慮すべきパターン数が多いときに検討するのがよいでしょう。

偶奇性を知りたい場合は、合同式を利用して\(\small (-1)^a\)の形を作り出すとうまくいくことが多い。今回の問題であれば、\(\small 3^a\)なので、-1余るようにするためにmod4を考えることにする。

問題文より\(\small b≧2\)なので、\(\small 2^b\)は必ず4の倍数（\(\small 2^b=4、8、16、\cdots\)）になることに注意すると、式①のmod4は

\begin{split}
3^a-2^b &\equiv 1 \pmod{4}\\
\Rightarrow \space \color{red}{(-1)}^a-\color{red}0 &\equiv 1 \pmod{4}\\
\Rightarrow \space (-1)^a&\equiv 1 \pmod{4}\\
\end{split}

この式が成り立つためには、\(\small a\)は偶数である必要がある（\(\small a\)が奇数だと左辺が-1になっちゃうので）。

(1)の結果より、\(\small b\)は正の整数（\(\small b≧1\)）なので、ここでは、\(\small b=1\)と\(\small b≧2\)の2パターンで場合分けして考える。

\(\small b=1\)の場合、\(\small a=1\)なので、\(\small \color{red}{(a,b)=(1,1) \cdots ①}\)。

\(\small b≧2\)の場合、(2)の結果より、\(\small a=2k\)（\(\small k=1、2、\cdots\)）とおけるので①式は、\(\small 3^{2k}-2^b=1\)とおける。このあと、何をするか手が止まってしまった人は、冒頭の解説編で紹介した解き方のポイントを思い出そう。

STEP1については(1)、(2)で絞り込めているので、この後すべきは因数分解ですね。

\begin{split}
3^{2k}-2^b&=1\\
3^{2k}-1&=2^b\\
(3^{k})^2-1^2&=2^b\\
(3^{k}+1)(3^{k}-1)&=2^b\\
\end{split}

途中の因数分解は\(\small a^2-b^2=(a+b)(a-b)\)を利用している。ここで、

\begin{cases}
3^{k}+1=2^p\cdots②\\
3^{k}-1=2^q\cdots③\\
\end{cases}

（\(\small p+q=b\)）とおいてみる。②-③で\(\small 3^k\)を消去すると

\begin{split}
2^p-2^q=2\\
2^q(2^{p-q}-1)=2
\end{split}

（補足）\(\small p、q\)の大小関係に注意
式②、③からわかるように、\(\small 3^{k}+1>3^{k}-1\)なので\(\small p<q\)となることに気を付けましょう。このことを踏まえると、\(\small 2^p-2^q=2\)を式変形するときは、解答のように指数が小さい\(\small 2^q\)でくくりださないといけません。
文字だけで分かりずらい人は、たとえば\(\small 2^5-2^2\)みたいにイメージしてもらうと、普通は\(\small 2^2(2^3-1)\)のように指数の小さい\(\small 2^2\)の方を括弧の外にくくりだすよね（指数が大きい方でくくると\(\small 2^5(1-2^{-3})\)となり式変形としては微妙）ということです。

[1] \(\small 2^q=1\)、\(\small 2^{p-q}-1=2\)の場合
\(\small 2^{p-q}=3\)となるが上記を満たす解はないため不適。

[2] \(\small 2^q=2\)、\(\small 2^{p-q}-1=1\)の場合
\(\small q=1\)なので、
\begin{split}
2^{p-1}-1&=1\\
2^{p-1}&=2^1\\
\Rightarrow \space p-1&=1\\
p&=2\\
\end{split}
よって、②、③に代入すると
\begin{split}
\begin{cases}
3^{k}+1=2^2\\
3^{k}-1=2^1\\
\end{cases}
\space\Rightarrow 3^k=3、k=1
\end{split}
すると、\(\small a=2k\)より、\(\small \color{red}{a=2}\)と求まるので、①式は
\begin{split}
3^a-2^b&=1\\
3^2-2^b&=1\\
2^b&=8\\
\Rightarrow \space \color{red}b&\color{red}{=3}
\end{split}
よって、\(\small \color{red}{(a,b)=(2,3)\cdots④}\)

よって、②、④より、\(\small \color{red}{(a,b)=(1,1)、(2,3)\cdots}\)（答）

【問題4】\(\small n\)乗を含む不定方程式の難問[九州大]

\(\small \dfrac{n^2+1}{2},\dfrac{n^2-1}{2}\)が互いに素であることを示す前に、大前提として、\(\small \dfrac{n^2+1}{2},\dfrac{n^2-1}{2}\)が整数なのか？ということを示しておこう。なぜならば、例えば\(\small n=2\)の場合、\(\small \dfrac{n^2+1}{2}=\dfrac{5}{2},\dfrac{n^2-1}{2}=\dfrac{3}{2}\)のように分数になるので、互いに素とかの前に整数じゃない…となってしまうからである。

\(\small \dfrac{n^2+1}{2},\dfrac{n^2-1}{2}\)が整数になるためには、分子が偶数であればよいので、\(\small n^2\)が奇数であればよい。2乗した数が奇数ならば、2乗する前の数も奇数なので（仮に偶数だったら、2乗しても偶数になる）、\(\small n\)が奇数であることを示せればよい。つまり、合同式で表すならば、\(\small \color{red}{n\equiv1 \pmod{2}}\)を示せればよい。

問題の式の両辺をmod2で考えると

\begin{split}
n^4&=1+210m^2\\
\Rightarrow \space n^4&\equiv 1+\color{red}0 \pmod{2}\\
\Rightarrow \space n^4&\equiv 1 \pmod{2}\\
\Rightarrow \space n&\equiv \pm 1 \pmod{2}\\
\Rightarrow \space n&\equiv 1 \pmod{2}\\
\end{split}

（補足）
最後の式変形は、mod2の場合、\(\small -1 \equiv 1 \pmod{2}\)を用いた。

よって、\(\small n\)が奇数であることが分かったので、\(\small \dfrac{n^2+1}{2},\dfrac{n^2-1}{2}\)が整数という大前提は示すことができた。

では続いて本題。互いに素であるということは、最大公約数が1であるということなので、

\begin{cases}
\dfrac{n^2+1}{2}=g\ell\\
\dfrac{n^2-1}{2}=gk
\end{cases}

（ただし、\(\small g、\ell、k\)は自然数）とおいて、\(\small g=1\)を示せればよい。

上式を式変形すると

\begin{split}
&\begin{cases}
n^2=2g\ell -1\\
n^2=2gk +1\\
\end{cases}\\
&\Rightarrow \space 2g\ell -1=2gk +1\\
&\qquad 2g(\ell-k)=2\\
& \qquad g(\ell-k)=1\\
\end{split}

よって、\(\small \color{red}{g=1}、\ell-k=1\)となるので、題意は示された。

ちなみに、この結果をもとの式に代入してあげると

\begin{cases}
\dfrac{n^2+1}{2}=k+1\\
\dfrac{n^2-1}{2}=k
\end{cases}

となり、それぞれ、連続する数であることが分かる。

王道的に、\(\small n^2-1=168k\)を示すという攻め方があるが、問題の式に4乗など高次の指数が含まれることからかなり厳しいので、合同式を使って168の倍数であることを調べていく方針が有効だろう。

\(\small 168=2^3 \times 3 \times 7\)なので、\(\small n^2-1\)が3の倍数かつ、7の倍数かつ、8の倍数を示せればよい。一旦問題文の式を変形して\(\small n^2-1\)の形を出しに行くと

\begin{split}
n^4&=1+210m^2\\
n^4&-1=210m^2\\
(n^2&-1)(n^2+1)=2\cdot3\cdot5\cdot7 m^2\quad\cdots(*)\\
\end{split}

ここで、\(\small (*)\)の両辺でmod3を考えると

\begin{split}
(n^2&-1)(n^2+1) \equiv 0 \pmod{3}\\
\Rightarrow &\space n^2 \equiv1 \pmod{3}\\
\Rightarrow &\space \color{red}{n^2 -1\equiv 0\pmod{3}}
\end{split}

よって3の倍数であることが確認できた。

7の倍数であることの確認も同様にmod7を考えることで

\begin{split}
(n^2&-1)(n^2+1) \equiv 0 \pmod{7}\\
\Rightarrow &\space n^2 \equiv1 \pmod{7}\\
\Rightarrow &\space \color{red}{n^2 -1\equiv 0\pmod{7}}
\end{split}

最後に8の倍数であることは、若干式変形が必要。まず\(\small (*)\)の両辺を4で割ると

\begin{split}
(n^2-1)&(n^2+1)=2\cdot3\cdot5\cdot7 m^2\\
\frac{(n^2-1)}{2}&\cdot\frac{(n^2+1)}{2}=\frac{3\cdot5\cdot7 m^2}{2}\\
\end{split}

(1)で左辺のかけ算はそれぞれ整数であることを確認したので、右辺も整数である必要があることから、\(\small m\)は偶数であることが確定する。\(\small m=2a\)とおくと

\begin{split}
\frac{(n^2-1)}{2}&\cdot\frac{(n^2+1)}{2}=2\cdot3\cdot5\cdot7 a^2\\
(n^2-1)&(n^2+1)=2^3\cdot3\cdot5\cdot7 a^2\\
\end{split}

この式でmod8を考えると、

\begin{split}
(n^2-1)&(n^2+1)\equiv0 \pmod{8}\\
\Rightarrow \space & \color{red}{n^2-1 \equiv0 \pmod{8}}\\
\end{split}

よって、8の倍数であることが確認できた。

上記の結果より、\(\small n^2-1\)が3の倍数かつ7の倍数かつ8の倍数であることが確認できたので、168の倍数であることが示された。

（補足）
他にも(1)の誘導を使って、\(\small n^2+1\)が3や7の倍数でないことを示す解法もあるが確認すべきパターンが多く大変なので、個人的には直接示す方が早いかなと思っています。

(2)の結果から、\(\small n^2-1=168\ell\)とおけるので、この結果を使って適当に整数解を見つければよい。\(\small (*)\)に代入して因数分解すると

\begin{split}
168\ell(168\ell+2)&=2\cdot3\cdot5\cdot7 m^2\\
8\ell(84\ell+1)&=5 m^2\\
\end{split}

両辺のmod5を考えると

\begin{split}
\color{red}3\ell(\color{red}{(-1)}\cdot\ell+1)&\equiv \color{red}0 \pmod{5}\\
3\ell(-\ell+1)&\equiv 0 \pmod{5}\\
\Rightarrow \space \ell\equiv &0、1 \pmod{5}
\end{split}

よって、\(\small \ell\)は5の倍数または5の倍数+1が解の候補になる。具体的には、\(\small \ell=5、6、10、11、15、16\cdots\)など。あとは順番に探していく。

[1] \(\small \ell=5\)の場合
\begin{split}
8\ell(84\ell+1)&=5 m^2\\
\Rightarrow \space 8\cdot5\cdot (84\cdot5&+1)=5 m^2\\
2^3\cdot421=&m^2\\
\end{split}
上記を満たす自然数\(\small m\)は存在しないため不適。

[2] \(\small \ell=6\)の場合
\begin{split}
8\ell(84\ell+1)&=5 m^2\\
\Rightarrow \space 2^3\cdot 6\cdot505&=5 m^2\\
\Rightarrow \space 2^4\cdot 3\cdot101&=m^2\\
\end{split}
上記を満たす自然数\(\small m\)は存在しないため不適。

[3] \(\small \ell=10\)の場合
\begin{split}
8\ell(84\ell+1)&=5 m^2\\
\Rightarrow \space 2^3\cdot 10\cdot841&=5 m^2\\
\Rightarrow \space 2^4\cdot29^2&=m^2\\
\Rightarrow \space (4\cdot29)^2&=m^2\\
\end{split}
上記を満たす自然数は\(\small m=116\)。

このとき、\(\small n^2=168\ell+1=168\cdot10+1=1681=41^2\)より、\(\small n=41\)。

よって、\(\small (m,n)=(116,41)\cdots\)(答)

【本記事のまとめ】\(\small n\)乗を含む不定方程式の整数解の求め方

今回は、\(\small n\)乗を含む不定方程式の整数解の求め方を難関大学の入試問題を通して解説していきました。解き方のポイントはズバリ「合同式を利用せよ」でした。合同式で解の条件を絞った後に因数分解で解を特定しに行くというアプローチでだいたいの問題は対処できるので、ぜひ他の問題にもチャレンジしてみてください。

他にも有名大学の整数問題を解きたいという人は、「【整数問題】3乗を含む不定方程式の整数解【有名大学入試の良問】【京大、千葉大、一橋大】」の記事もあるのでぜひチャレンジしてみてください！

では、今回はここまでです。お疲れさまでした！