今回はド・モアブルの定理を利用する典型問題の一種である複素数のn乗根を求める問題について徹底解説していきます。また、大学入試などでもよく題材として取り上げられる\(\small n\)乗根の解が複素数平面上で持つ図形的な意味合いについても解説していきます。一つ一つ順番に理解していけば誰でも理解できる内容だと思うので、一緒に確認していきましょう!
- ド・モアブルの定理を利用した複素数の\(\small n\)乗根の求め方を知りたい人
- 複素数の\(\small n\)乗根が持つ図形的な意味合いについて理解したい人
- 定期テスト対策、受験対策がしたい人
【問題&解説】n乗根に関する問題
本記事では以下の問題を解説していきます。
次の方程式を解け。
(1)\(\small z^6 = 27\)
(2)\(\small z^3 = 8i\)
(3)\(\small z^3 = -4i\)
(4)\(\small z^4 = -9\)
問題1の解説はこちら
\(\small x=\cos \theta +i\sin\theta\)とおく。\(\small 0≦\theta <2\pi\)の範囲で、方程式 \(\small 2x^5 = \sqrt{3}+i\)を満たす\(\small \theta \)を求めよ。 [山形大]
問題2の解説はこちら
複素数平面上において、\(\small z^3=4+4\sqrt{3}i\)の解を \(\small z_n\)(\(\small n=1,2,3\))とし、それぞれ\(\small \mathrm{P}(z_1)\), \(\small \mathrm{Q}(z_2)\), \(\small \mathrm{R}(z_3)\)とする。このとき、\(\small △\mathrm{PQR}\)の面積を求めよ。
問題3の解説はこちら
【問題1】複素数のn乗根を求める問題(難易度:★☆☆)
次の方程式を解け。
(1)\(\small z^6 = 27\)
(2)\(\small z^3 = 8i\)
(3)\(\small z^3 = -4i\)
(4)\(\small z^4 = -9\)
① 左辺を\(\small z = r(\cos \theta +i\sin \theta)\)とおいてド・モアブルの定理を適用
② 右辺を極形式に変換
③ 両辺の原点からの距離と偏角を比較
・右辺の極形式への変換は以下4パターンを押さえておけばOK。
\begin{split}
\small 1 &\small \displaystyle = \cos 2k\pi + i \sin 2k\pi\\
\small \displaystyle i &\small \displaystyle= \cos \left(\frac{\pi}{2}+2k\pi\right) + i \sin \left(\frac{\pi}{2}+2k\pi\right)\\
\small \displaystyle -1 &\small \displaystyle= \cos (2k+1)\pi + i \sin (2k+1)\pi\\
\small \displaystyle -i &\small \displaystyle= \cos \left(\frac{3\pi}{2}+2k\pi\right) + i \sin \left(\frac{3\pi}{2}+2k\pi\right)\\
\end{split}
↓↓ド・モアブルの定理について詳しく知りたい人はこちらの記事をチェック!↓↓
【数C_複素数平面】ド・モアブルの定理とは?複素数の累乗計算を分かりやすく解説
\begin{split}
\small z &\small = \sqrt[n]{r}(\cos \theta +i\sin \theta )^{\frac{1}{n}}\\
&\small = \sqrt[n]{r}\left(\cos \frac{\theta}{n} +i\sin \frac{\theta}{n} \right)\\
\end{split}
のように解くのはダメなのでしょうか?
結論、この解法は誤りとなります。理由は、複素数の世界では非整数乗はうまく定義できないからです(非整数とは\(\small 1/2, -3/4\)といった分数のこと)。どういうことか具体例で説明すると、例えば、複素数の非整数乗として\(\small (-1)^{\frac{1}{2}}\)を考えてみましょう。これは一見すると、\(\small (-1)^{\frac{1}{2}}=\sqrt{-1}=i\)となりそうですが、一方で、
\begin{split}
\small (-1)^{\frac{1}{2}} &\small = \left(\frac{1}{-1}\right)^{\frac{1}{2}}\\
&\small = \frac{1}{i}\\
&\small = \frac{1 \cdot i}{i \cdot i}\\
&\small = -i\\
\end{split}
と計算することもできるので、\(\small (-1)^\frac{1}{2}= i = -i\)というおかしな関係が成り立ってしまいます。
このように、複素数の指数が整数でない場合は計算結果が一意に定まらないことが分かります。
なので、冒頭のように\(\small \displaystyle \frac{1}{n}\)乗に対してド・モアブルの定理を利用してしまうのは、指数が整数ではないので不適切というわけです。
\(\small z\)を原点からの距離が\(\small r\)(\(\small r\)は正の実数)、偏角が\(\small \theta \)(\(\small 0≦\theta <2\pi\))の複素数とすると、その極形式は\(\small z=r(\cos \theta +i\sin \theta) \)とおけるので、方程式の左辺は
\begin{split}
\small z^6 &\small =r^6(\cos \theta +i\sin \theta )^6\\
&\small =r^6(\cos 6\theta +i\sin 6\theta ) \quad ◀ド・モアブルの定理\\
\end{split}
左辺がド・モアブルの定理で極形式の形になっているので、右辺も極形式で表すと
\begin{split}
\small 27 &\small = 27 \cdot \color{#ef5350}{1}\\
&\small = 27\color{#ef5350}{\left(\cos 2k\pi +i\sin 2k\pi\right)}\\
\end{split}
ただし、\(\small k\)は整数。
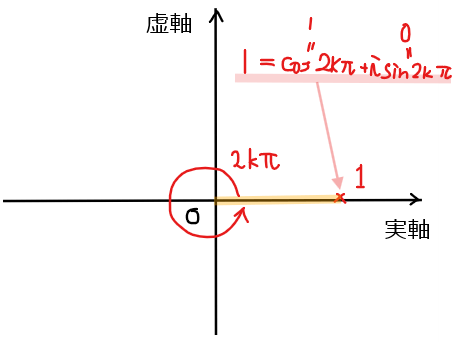
【補足】なぜ極形式の偏角を一般角にするのか?
「1」を表す複素数は、\(\small 0~2\pi\)までの偏角で考えるならば、\(\small \cos 0 +i\sin 0\)と表せるが、なぜ偏角を一般角として\(\small \cos 2k\pi +i\sin 2k\pi\)とする必要があるのだろうか?
答えは、\(\small n\)乗した後の複素数の偏角は一般的には\(\small 0~2\pi\)の範囲にあるとは限らないからだ。本問であえば、複素数 \(\small z\)自体の偏角は\(\small 0≦\theta <2\pi\)を満たすが、\(\small z^6\)の偏角はド・モアブルの定理から\(\small 6\theta\)なので、\(\small 0≦6\theta <12\pi\)の範囲で考える必要がある。そのため、まずは極形式の偏角は一般角で考えておき、そのあとで整数\(\small k\)が取り得る範囲を絞り込んでいくのがよい。
よって、これらの結果をもとの方程式に代入すると
\begin{split}
\small \displaystyle z^6 &\small = 27\\
\small \Leftrightarrow \space \displaystyle r^6\color{#ef5350}{(\cos 6\theta +i\sin 6\theta)} &\small = 27\color{#ef5350}{\left(\cos 2k\pi +i\sin 2k\pi\right)} \\
\end{split}
よって、両辺が等しくなるためには原点からの距離と偏角が両辺で一致している必要があるので、
\begin{cases}
\small r^6 = 27 \quad \cdots ①\\
\small 6 \theta = 2k\pi \quad \cdots ②\\
\end{cases}
あとは上記の方程式をそれぞれ解いて、\(\small r\)と\(\small \theta \)を求めればよい。
まず①を解くと、
\begin{split}
&\small r^6 = 3^3\\
\small \Leftrightarrow \space &\small r = (3^3)^{\frac{1}{6}} \space ◀ \space r > 0\\
\small \Leftrightarrow \space &\small r = 3^{\frac{1}{2}}\\
\small \Leftrightarrow \space &\small r = \sqrt{3} \space \cdots ③\\
\end{split}
次に②を解くと
\begin{split}
&\small 6\theta = 2k\pi\\
\small \Leftrightarrow \space &\small \theta = \frac{k\pi}{3} \quad \cdots ④\\
\end{split}
ここで、偏角\(\small \theta\)は\(\small 0≦ \theta < 2\pi\)を満たす必要があるので
\begin{split}
&\small 0≦ \theta < 2\pi\\
\small \Leftrightarrow \space &\small 0≦ 6\theta < 12\pi\\
\small \Leftrightarrow \space &\small 0≦ 2k\pi < 12\pi\\
\small \Leftrightarrow \space &\small 0≦ k < 6\\
\end{split}
\(\small k\)は整数なので、上記不等式を満たす具体的な\(\small k\)はの値を書き下すと\(\small k=0,1,2,3,4,5\)。
よって、これらの\(\small k\)の値を④の式に代入することで偏角の値はそれぞれ
\begin{split}
&\small \theta_0 = 0, \theta _1 = \frac{\pi}{3},\\
&\small \theta_2 = \frac{2}{3}\pi, \theta _3 = \pi,\\
&\small \theta_4 = \frac{4}{3}\pi, \theta _5 = \frac{5}{3}\pi\\
\end{split}
と求めることができる。これで原点からの距離が\(\small \sqrt{3}\)(∵ ③)、偏角が\(\small \theta_k\)(\(\small k=0,1,2,3,4,5\))の複素数が求める解になるので、極形式で表せば
\begin{split}
\small \displaystyle z_k &\small = \sqrt{3}(\cos \theta_k + i\sin \theta_k) \quad \cdots ⑤\\
\end{split}
⑤にこれまでの結果を代入したものが答えになる。
[i] \(\small k=0\)のとき
\begin{split}
\small z_0 &\small \displaystyle = \sqrt{3}\left(\cos 0 + i\sin 0\right) \\
&\small \displaystyle = \color{red}{\sqrt{3} \space \cdots 【答】}\\
\end{split}
[ii] \(\small k=1\)のとき
\begin{split}
\small z_1 &\small \displaystyle = \sqrt{3}\left(\cos \frac{\pi}{3} + i\sin \frac{\pi}{3}\right) \\
&\small \displaystyle = \sqrt{3}\left(\frac{1}{2}+\frac{\sqrt{3}}{2}i\right)\\
&\small \displaystyle = \color{red}{\frac{\sqrt{3}}{2}+\frac{3}{2}i \space \cdots 【答】}\\
\end{split}
[iii] \(\small k=2\)のとき
\begin{split}
\small z_2 &\small \displaystyle = \sqrt{3}\left(\cos \frac{2}{3}\pi + i\sin \frac{2}{3}\pi\right) \\
&\small \displaystyle = \sqrt{3}\left(-\frac{1}{2}+\frac{\sqrt{3}}{2}i\right)\\
&\small \displaystyle = \color{red}{-\frac{\sqrt{3}}{2}+\frac{3}{2}i \space \cdots 【答】}\\
\end{split}
[iv] \(\small k=3\)のとき
\begin{split}
\small z_3 &\small \displaystyle = \sqrt{3}\left(\cos \pi + i\sin \pi\right) \\
&\small \displaystyle = \color{red}{-\sqrt{3} \space \cdots 【答】}\\
\end{split}
[v] \(\small k=4\)のとき
\begin{split}
\small z_4 &\small \displaystyle = \sqrt{3}\left(\cos \frac{4}{3}\pi + i\sin \frac{4}{3}\pi\right) \\
&\small \displaystyle = \sqrt{3}\left(-\frac{1}{2}-\frac{\sqrt{3}}{2}i \right)\\
&\small \displaystyle = \color{red}{-\frac{\sqrt{3}}{2}-\frac{3}{2}i \space \cdots 【答】}\\
\end{split}
[vi] \(\small k=5\)のとき
\begin{split}
\small z_5 &\small \displaystyle = \sqrt{3}\left(\cos \frac{5}{3}\pi + i\sin \frac{5}{3}\pi\right) \\
&\small \displaystyle = \sqrt{3}\left(-\frac{1}{2}-\frac{\sqrt{3}}{2}i \right)\\
&\small \displaystyle = \color{red}{-\frac{\sqrt{3}}{2}-\frac{3}{2}i \space \cdots 【答】}\\
\end{split}
$$\small \displaystyle z_k = \sqrt[n]{a}\left(\cos \frac{2k\pi}{n} + i\sin \frac{2k\pi}{n}\right) \quad (k=0,1,\cdots,n-1)$$
と表される。
*略解*
\(\small a= a(\cos 2k\pi+i\sin 2k\pi)\)、\(\small z =r(\cos \theta +i\sin\theta) \)として方程式に代入すると
$$\small r^n(\cos n\theta +i\sin n\theta)=a(\cos 2k\pi +i\sin 2k\pi)$$
となることから\(\small r,\theta\)を求めると上式を導ける。
\(\small k\)の値の範囲も、偏角\(\small \theta \)が\(\small 0≦ \theta <2\pi\)を満たすことから求めることができる。
\(\small z = r(\cos\theta +i\sin\theta)\)(\(\small r\)は正の実数、\(\small 0≦\theta <2\pi\))とおく。
方程式の左辺は
\begin{split}
&\small z^3= r^3(\cos 3\theta +i\sin 3\theta)\\
\end{split}
一方、右辺を極形式で表すと
\begin{split}
\small 8\color{#ef5350}i = 8\color{#ef5350}{\left(\cos \frac{\pi}{2}+i\sin \frac{\pi}{2}\right)}\\
\end{split}
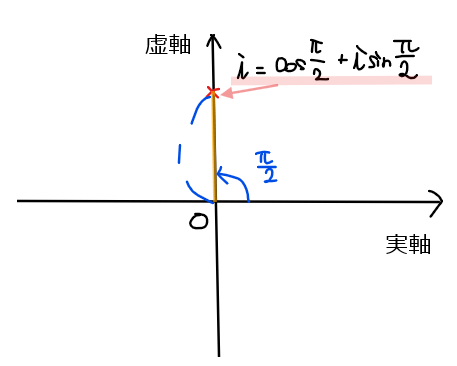
より、偏角の一般形としては
\begin{split}
\small 8i = 8\left(\cos \left(\frac{\pi}{2}+\color{red}{2k\pi}\right)+i\sin\left(\frac{\pi}{2}+\color{red}{2k\pi} \right)\right) \\
\end{split}
(ただし、\(\small k\)は整数)。
以上より、問題の方程式は
\begin{split}
\small z^3 &\small = 8i\\
\small \Leftrightarrow \space r^3(\cos 3\theta +i\sin 3\theta) &\small= 8\left(\cos \left(\frac{\pi}{2}+2k\pi\right)+i\sin\left(\frac{\pi}{2}+2k\pi\right)\right) \\
\end{split}
よって、両辺の原点からの距離と偏角を比較することで
\begin{cases}
\small r^3 = 8 \space \cdots ①\\
\small \displaystyle 3\theta = \frac{\pi}{2}+2k\pi \space \cdots ②\\
\end{cases}
①は\(\small r\)が原点からの距離、すなわち正の実数であることを踏まえると、\(\small r= 2\) …③。
②は、\(\small \theta \)について解くと
\begin{split}
&\small \displaystyle \theta = \frac{\pi}{6}+\frac{2k\pi}{3} \space \cdots ④\\
\end{split}
また、整数\(\small k\)の取り得る範囲は、偏角が\(\small 0≦\theta < 2\pi\)であることから
\begin{split}
&\small \displaystyle 0≦\theta <2\pi\\
\small \Leftrightarrow \space &\small \displaystyle 0≦\frac{\pi}{6}+\frac{2k\pi}{3} <2\pi \quad ◀④を代入\\
\small \Leftrightarrow \space &\small \displaystyle 0≦\frac{4k+1}{6}\pi <2\pi\\
\small \Leftrightarrow \space &\small \displaystyle 0≦4k+1 <12\\
\small \Leftrightarrow \space &\small \displaystyle -\frac{1}{4}≦k <\frac{11}{4}\\
\end{split}
上記の不等式を満たす整数\(\small k\)は\(\small k= 0,1,2\)。
あとは、それぞれの\(\small k\)の値に対応する偏角\(\small \theta\)を④に代入することで求めると、
\begin{split}
\begin{cases}
\small \displaystyle \theta_0 = \frac{\pi}{6}\\
\small \displaystyle \theta_1 = \frac{\pi}{6}+\frac{2}{3}\pi=\frac{5}{6}\pi\\
\small \displaystyle \theta_2 = \frac{\pi}{6}+\frac{4}{3}\pi=\frac{3}{2}\pi\\
\end{cases}
\small \quad \cdots ⑤\\
\end{split}
となるので、方程式を満たす解は、③、⑤より、\(\small z_k = 2(\cos \theta_k+i\sin \theta_k)\)となるので
[i] \(\small k= 0\)のとき
\begin{split}
\small z_0 &\small \displaystyle =2\left(\cos \frac{\pi}{6}+i\sin \frac{\pi}{6}\right)\\
&\small \displaystyle =2\left(\frac{\sqrt{3}}{2}+\frac{1}{2} i \right)\\
&\small \displaystyle =\color{red}{\sqrt{3}+i \quad \cdots 【答】}\\
\end{split}
[ii] \(\small k= 1\)のとき
\begin{split}
\small z_1 &\small \displaystyle =2\left(\cos \frac{5\pi}{6}+i\sin \frac{5\pi}{6}\right)\\
&\small \displaystyle =2\left(-\frac{\sqrt{3}}{2}+\frac{1}{2} i \right)\\
&\small \displaystyle =\color{red}{-\sqrt{3}+i \quad \cdots 【答】}\\
\end{split}
[iii] \(\small k= 2\)のとき
\begin{split}
\small z_2 &\small \displaystyle =2\left(\cos \frac{3\pi}{2}+i\sin \frac{3\pi}{2}\right)\\
&\small \displaystyle =2\left(0-i \right)\\
&\small \displaystyle =\color{red}{-2i \quad \cdots 【答】}\\
\end{split}
\(\small z = r(\cos\theta +i\sin\theta)\)(\(\small r\)は正の実数、\(\small 0≦\theta <2\pi\))とおく。
方程式の左辺は
\begin{split}
&\small z^3= r^3(\cos 3\theta +i\sin 3\theta)\\
\end{split}
一方、右辺を極形式で表すと
\begin{split}
\small -4i &\small = 4 \cdot \color{#ef5350}{(-i)}\\
&\small =4\color{#ef5350}{\left\{\cos \left(\frac{3}{2}\pi +2k\pi \right) +i\sin \left(\frac{3}{2}\pi +2k\pi \right)\right\}} \quad [*1]\\
\end{split}
(ただし、\(\small k\)は整数)。
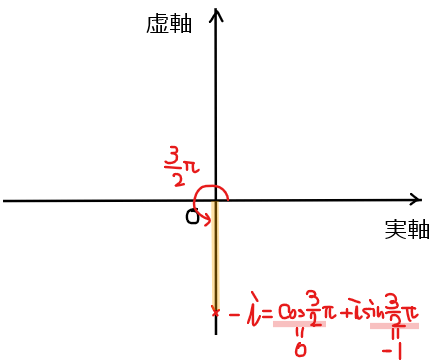
*1:【補足】\(\small -i\)の極形式の一般角
偏角が\(\small 0 ≦ \theta <2\pi\)の範囲では、\(\small \displaystyle -i =\cos \frac{3}{2}\pi+i\sin \frac{3}{2}\pi\)であることから、一般形では1周分角度がズレているものも三角比としては同じ値になるので、\(\small 2k\pi\)(\(\small k\):整数)を角度に付けてあげればよい。
よって、問題の方程式は
\begin{split}
\small z^3 &\small = -4i\\
\small \Leftrightarrow \space r^3(\cos 3\theta +i\sin 3\theta) &\small= 4\left\{\cos \left(\frac{3}{2}\pi +2k\pi \right) +i\sin \left(\frac{3}{2}\pi +2k\pi \right)\right\} \\
\end{split}
よって、両辺の原点からの距離と偏角を比較することで
\begin{split}
&\small r^3 = 4\\
\small ∴ \space &\small r = \sqrt[3]{4} \quad (∵ \space r>0) \space \cdots ①\\
\end{split}
\begin{split}
&\small \displaystyle 3\theta = \frac{3}{2}\pi +2k\pi\\
\small \Leftrightarrow \space &\small \displaystyle \theta = \frac{\pi}{2} +\frac{2k\pi}{3}\\
\small ∴ \space &\small \displaystyle \theta = \frac{4k+3}{6}\pi \space \cdots ②\\
\end{split}
②の偏角\(\small \theta\)は、\(\small k\)の値を求めると
\begin{split}
&\small \displaystyle 0≦\theta <2\pi\\
\small \Leftrightarrow \space &\small \displaystyle 0≦\frac{4k+3}{6}\pi <2\pi\\
\small \Leftrightarrow \space &\small \displaystyle 0≦4k+3 <12\\
\small \Leftrightarrow \space &\small \displaystyle -\frac{3}{4}≦k<\frac{9}{4}\\
\end{split}
\(\small k\)は整数であることから、上記の不等式を満たすのは\(\small k= 0,1,2\)。
よって、各\(\small k\)の値に対応する偏角\(\small \theta \)は②に代入することで
\begin{split}
\begin{cases}
\small \displaystyle \theta_0 = \frac{\pi}{2}\\
\small \displaystyle \theta_1 = \frac{7}{6}\pi\\
\small \displaystyle \theta_2 = \frac{11}{6}\pi\\
\end{cases}
\small \quad \cdots ③\\
\end{split}
①、③より、方程式を満たす解は、\(\small z_k = \sqrt[3]{4}(\cos \theta_k+i\sin \theta_k)\)となるので
[i] \(\small k= 0\)のとき
\begin{split}
\small z_0 &\small \displaystyle =\sqrt[3]{4}\left(\cos \frac{\pi}{2}+i\sin \frac{\pi}{2}\right)\\
&\small \displaystyle =\sqrt[3]{4}\left(0+i \right)\\
&\small \displaystyle =\color{red}{\sqrt[3]{4}i \quad \cdots 【答】}\\
\end{split}
[ii] \(\small k= 1\)のとき
\begin{split}
\small z_1 &\small \displaystyle =\sqrt[3]{4}\left(\cos \frac{7\pi}{6}+i\sin \frac{7\pi}{6}\right)\\
&\small \displaystyle =\sqrt[3]{4}\left(-\frac{\sqrt{3}}{2}-\frac{1}{2}i \right)\\
&\small \displaystyle =\color{red}{-\frac{\sqrt[3]{4}}{2}\left(\sqrt{3}+i \right) \quad \cdots 【答】}\\
\end{split}
[iii] \(\small k= 2\)のとき
\begin{split}
\small z_2 &\small \displaystyle =\sqrt[3]{4}\left(\cos \frac{11\pi}{6}+i\sin \frac{11\pi}{6}\right)\\
&\small \displaystyle =\sqrt[3]{4}\left(\frac{\sqrt{3}}{2}-\frac{1}{2}i \right)\\
&\small \displaystyle =\color{red}{\frac{\sqrt[3]{4}}{2}\left(\sqrt{3}-i \right) \quad \cdots 【答】}\\
\end{split}
\(\small z = r(\cos\theta +i\sin\theta)\)(\(\small r\)は正の実数、\(\small 0≦\theta <2\pi\))とおく。
方程式の左辺は
\begin{split}
&\small z^4= r^4(\cos 4\theta +i\sin 4\theta)\\
\end{split}
一方、右辺を極形式で表すと
\begin{split}
\small -9 &\small = 9 \cdot \color{#ef5350}{(-1)}\\
&\small =4\color{#ef5350}{(\cos (2k+1)\pi +i\sin (2k+1)\pi)} \quad [*1]\\
\end{split}
(ただし、\(\small k\)は整数)。
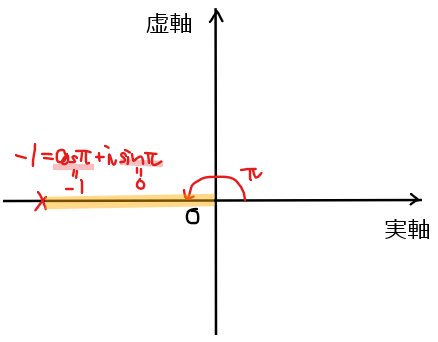
*1:【補足】\(\small -1\)の極形式の一般角
\(\small -1\)は複素数平面上では偏角が\(\small \pi\)や\(\small 3\pi\), \(\small 5\pi\)など『(奇数)\(\small \times \pi\)』となることから、\(\small (2k+1)\pi\)としている。もちろん、\(\small -1 = \cos \pi+i\sin \pi \)なので、偏角を一般角に直して(\(\small 2k\pi\)を付けて)、
\begin{split}
\small \cos \pi+i\sin \pi &\small = \cos (\pi+2k\pi)+i\sin (\pi+2k\pi) \\
&\small = \cos (2k+1)\pi+i\sin (2k+1)\pi\\
\end{split}
のように導き出してもOK。
よって、問題の方程式は
\begin{split}
\small z^4 &\small = -9\\
\small \Leftrightarrow \space r^4(\cos 4\theta +i\sin 4\theta) &\small= 9(\cos (2k+1)\pi +i\sin (2k+1)\pi)\\
\end{split}
よって、両辺の原点からの距離と偏角を比較することで
\begin{split}
&\small r^4 = 9\\
\small ∴ \space &\small r = \sqrt{3} \quad (∵ \space r>0) \space \cdots ①\\
\end{split}
\begin{split}
&\small \displaystyle 4\theta = (2k+1)\pi\\
\small \Leftrightarrow \space &\small \displaystyle \theta = \frac{(2k+1)\pi}{4} \space \cdots ②\\
\end{split}
②の偏角\(\small \theta\)は、\(\small k\)の値を求めると
\begin{split}
&\small \displaystyle 0≦\theta <2\pi\\
\small \Leftrightarrow \space &\small \displaystyle 0≦\frac{(2k+1)\pi}{4} <2\pi\\
\small \Leftrightarrow \space &\small \displaystyle 0≦(2k+1)\pi <8\pi\\
\small \Leftrightarrow \space &\small \displaystyle -\frac{1}{2}≦k<\frac{7}{2}\\
\end{split}
\(\small k\)は整数であることから、上記の不等式を満たすのは\(\small k= 0,1,2,3\)。
よって、各\(\small k\)の値に対応する偏角\(\small \theta \)は②に代入することで
\begin{split}
\begin{cases}
\small \displaystyle \theta_0 = \frac{\pi}{4}\\
\small \displaystyle \theta_1 = \frac{3}{4}\pi\\
\small \displaystyle \theta_2 = \frac{5}{4}\pi\\
\small \displaystyle \theta_3 = \frac{7}{4}\pi\\
\end{cases}
\small \quad \cdots ③\\
\end{split}
①、③より、方程式を満たす解は、\(\small z_k = \sqrt{3}(\cos \theta_k+i\sin \theta_k)\)となるので
[i] \(\small k= 0\)のとき
\begin{split}
\small z_0 &\small \displaystyle =\sqrt{3}\left(\cos \frac{\pi}{4}+i\sin \frac{\pi}{4}\right)\\
&\small \displaystyle =\sqrt{3}\left(\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}}i \right)\\
&\small \displaystyle =\color{red}{\frac{\sqrt{6}}{2}\left(1+i \right) \quad \cdots 【答】}\\
\end{split}
[ii] \(\small k= 1\)のとき
\begin{split}
\small z_1 &\small \displaystyle =\sqrt{3}\left(\cos \frac{3\pi}{4}+i\sin \frac{3\pi}{4}\right)\\
&\small \displaystyle =\sqrt{3}\left(-\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}}i \right)\\
&\small \displaystyle =\color{red}{\frac{\sqrt{6}}{2}\left(-1+i \right) \quad \cdots 【答】}\\
\end{split}
[iii] \(\small k= 2\)のとき
\begin{split}
\small z_2 &\small \displaystyle =\sqrt{3}\left(\cos \frac{5\pi}{4}+i\sin \frac{5\pi}{4}\right)\\
&\small \displaystyle =\sqrt{3}\left(-\frac{1}{\sqrt{2}}-\frac{1}{\sqrt{2}}i \right)\\
&\small \displaystyle =\color{red}{-\frac{\sqrt{6}}{2}\left(1+i \right) \quad \cdots 【答】}\\
\end{split}
[iii] \(\small k= 3\)のとき
\begin{split}
\small z_3 &\small \displaystyle =\sqrt{3}\left(\cos \frac{7\pi}{4}+i\sin \frac{7\pi}{4}\right)\\
&\small \displaystyle =\sqrt{3}\left(\frac{1}{\sqrt{2}}-\frac{1}{\sqrt{2}}i \right)\\
&\small \displaystyle =\color{red}{\frac{\sqrt{6}}{2}\left(1-i \right) \quad \cdots 【答】}\\
\end{split}
【問題2】n乗根の方程式の解と極形式(難易度:★☆☆)
\(\small x=\cos \theta +i\sin\theta\)とおく。\(\small 0≦\theta <2\pi\)の範囲で、方程式 \(\small 2x^5 = \sqrt{3}+i\)を満たす\(\small \theta \)を求めよ。 [山形大]
・\(\small \displaystyle \frac{\sqrt{3}}{2}+\frac{1}{2}i\)を極形式に変換する際に、\(\small \displaystyle \cos \frac{\pi}{6}+i\sin \frac{\pi}{6}\)のように偏角の範囲を\(\small 0~2\pi\)に限定しないように注意!
⇒ 本問は \(\small \displaystyle \frac{\sqrt{3}}{2}+\frac{1}{2}i\)の5乗根を求める問題なので、5乗する前の複素数の偏角\(\small \theta\)は\(\small 0≦\theta <2\pi\)の範囲内になるが、5乗した後の複素数は偏角が\(\small 5\)倍になるので、\(\small 0≦5\theta <10\pi\)の範囲となり、\(\small 0~2\pi\)の範囲内になるとは限らない。
問題の方程式は
\begin{split}
\small x^5 &\small \displaystyle =\frac{\sqrt{3}}{2}+\frac{1}{2}i\\
\small \Leftrightarrow \space x^5 &\small \displaystyle =\cos \color{#ef5350}{\left(\frac{\pi}{6}+2k\pi\right)}+i\sin \color{#ef5350}{\left(\frac{\pi}{6}+2k\pi\right)}\\
\end{split}
(ただし\(\small k\)は整数)と式変形できることから、\(\small x = \cos \theta +i\sin\theta\)を代入することで
\begin{split}
\small (\cos \theta +i\sin\theta)^5 &\small \displaystyle =\cos \left(\frac{\pi}{6}+2k\pi\right)+i\sin \left(\frac{\pi}{6}+2k\pi\right)\\
\small \Leftrightarrow \space \cos 5\theta +i\sin 5\theta &\small \displaystyle =\cos \left(\frac{\pi}{6}+2k\pi\right)+i\sin \left(\frac{\pi}{6}+2k\pi\right)\\
\end{split}
両辺が等しいことから、左右の複素数の原点からの距離と偏角が等しくなる。原点からの距離はどちらも\(\small 1\)で一致しているので偏角に注目すると
\begin{split}
\small 5\theta &\small \displaystyle =\frac{\pi}{6}+2k\pi\\
\small ∴ \space \theta &\small \displaystyle =\frac{\pi}{30} +\frac{2k\pi}{5} \quad \cdots ①\\
\end{split}
問題の条件から、\(\small \theta\)は\(\small 0≦\theta<2\pi \)を満たす必要があるので
\begin{split}
&\small \displaystyle 0≦\frac{\pi}{30} +\frac{2k\pi}{5}<2\pi\\
\small \Leftrightarrow \space &\small \displaystyle 0≦12k+1<60\\
\small \Leftrightarrow \space &\small \displaystyle -\frac{1}{12}≦k<\frac{59}{12}\\\
\end{split}
\(\small k\)は整数であることから、上記の不等式を満たすのは \(\small k = 0,1,2,3,4\)。
よって、①にそれぞれ\(\small k\)の値を代入することで求める\(\small \theta\)の値は
\begin{split}
&\small \displaystyle \color{red}{\theta = \frac{\pi}{30},\frac{13\pi}{30},\frac{5\pi}{6},\frac{37\pi}{30},\frac{49\pi}{30}\quad \cdots 【答】}
\end{split}
【問題3】n乗根の図形的性質を利用した問題(難易度:★★☆)
複素数平面上において、\(\small z^3=4+4\sqrt{3}i\)の解を \(\small z_n\)(\(\small n=1,2,3\))とし、それぞれ\(\small \mathrm{P}(z_1)\), \(\small \mathrm{Q}(z_2)\), \(\small \mathrm{R}(z_3)\)とする。このとき、\(\small △\mathrm{PQR}\)の面積を求めよ。
・上記の図形的性質を踏まえると本問の解を頂点とする\(\small △\mathrm{PQR}\)は正三角形となるため、1辺の長さが求まれば面積を求めることができます。
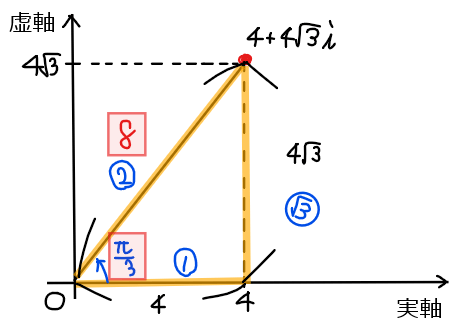
\(\small 4+4\sqrt{3}i\)を極形式で表すと
\begin{split}
&\small \displaystyle 4+4\sqrt{3}i=8\left(\cos \left(\frac{\pi}{3}+2k\pi\right)+i\sin \left(\frac{\pi}{3}+2k\pi\right)\right)\\
\end{split}
(ただし、\(\small k\)は整数)。
\(\small z = r(\cos \theta+i\sin \theta)\)(\(\small 0≦ \theta < 2\pi\))とすると、ド・モアブルの定理より
\begin{split}
\small \displaystyle z^3 &\small=4+4\sqrt{3}i\\
\small \Leftrightarrow \space \displaystyle r^3(\cos 3\theta +i\sin 3\theta) &\small =8\left(\cos \left(\frac{\pi}{3}+2k\pi\right)+i\sin \left(\frac{\pi}{3}+2k\pi\right)\right)\\
\end{split}
上式の両辺の原点からの距離と偏角を比較することで
\begin{split}
\small \displaystyle r^3 &\small = 8\\
\small ∴ \space \displaystyle r &\small= 2 \space \cdots ①\\
\end{split}
\begin{split}
\small \displaystyle 3\theta &\small = \frac{\pi}{3}+2k\pi\\
\small ∴ \space \displaystyle \theta &\small= \frac{6k+1}{9}\pi \space \cdots ②\\
\end{split}
①から複素数\(\small z_1,z_2,z_3\)はすべて原点からの距離が\(\small 2\)であることが分かる。
\(\small k\)の値が取り得る範囲としては、
\begin{split}
&\small 0≦\theta <2\pi\\
\small \Leftrightarrow \space &\small \displaystyle 0≦ \frac{6k+1}{9}\pi <2\pi\\
\small \Leftrightarrow \space &\small \displaystyle 0≦ 6k+1 <18\\
\small \Leftrightarrow \space &\small \displaystyle -\frac{1}{6}≦ k <\frac{17}{6}\\
\end{split}
上記不等式を満たす整数 \(\small k\)の値は、\(\small k=0,1,2\)。
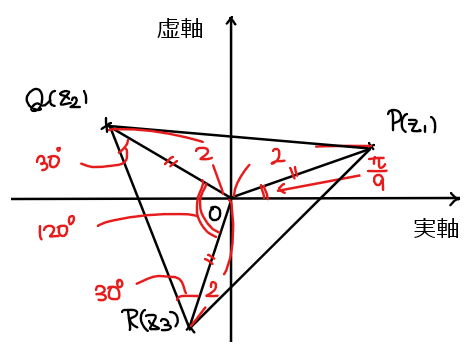
よって、②に代入することで、\(\small z_1、z_2、z_3\)の偏角はそれぞれ\(\small \displaystyle \theta_1 =\frac{\pi}{9} \), \(\small \displaystyle \theta_2 =\frac{7\pi}{9} \), \(\small \displaystyle \theta_3 =\frac{13\pi}{9} \)となる。
以上より、\(\small z_1、z_2、z_3\)の解を複素数平面上に図示すると以下のようになることから、\(\small △\mathrm{PQR}\)は正三角形 [*1]となる。
*1:【補足】正三角形になることの確認
\begin{split}
&\small \angle \mathrm{QOR} =\theta_3-\theta_2\\
&\small \displaystyle =\frac{13\pi}{9}-\frac{7\pi}{9}\\
&\small \displaystyle =\frac{2\pi}{3}\space (=120°)\\
\end{split}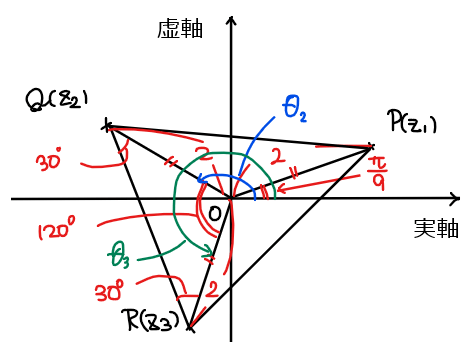
また、\(\small \mathrm{OQ}= \mathrm{OR}=2\)(複素数\(\small z_2,z_3\)の原点からの距離が\(\small 2\)だから)であることから、\(\small △\mathrm{OQR}\)は頂角が\(\small 120°\)の二等辺三角形なので、底角 \(\small \angle \mathrm{OQR} =\angle = \mathrm{ORQ} =30°\)。
\(\small △\mathrm{OPQ},△\mathrm{OPR}\)についても同様の計算すると同じ結果になることから、\(\small \angle \mathrm{PQR} =\angle \mathrm{QRP} = \angle \mathrm{RPQ}=60°\)となり正三角形であることが確認できる。
1辺の長さは\(\small △\mathrm{OQR}\)に着目することで、\(\small \mathrm{QR}=2\sqrt{3}\)と求めることができる。
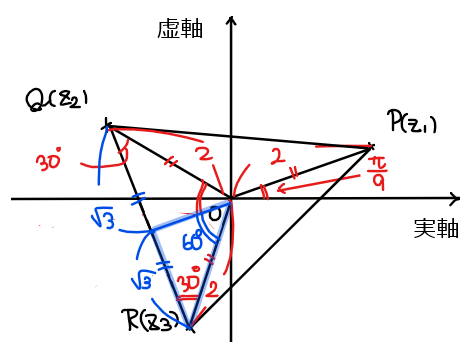
よって、\(\small △\mathrm{PQR}\)の面積は
\begin{split}
\small △\mathrm{PQR} &\small = \frac{1}{2}\mathrm{QP}\cdot \mathrm{QR}\sin \angle \mathrm{PQR}\\
&\small = \frac{1}{2}\times 2\sqrt{3} \times 2\sqrt{3}\times \sin \frac{\pi}{3}\\
&\small = 6\times \frac{\sqrt{3}}{2}\\
&\small = \color{red}{3\sqrt{3} \space \cdots 【答】}\\
\end{split}
本記事のまとめ
今回はド・モアブルの定理を利用した\(\small n\)乗根の求め方と図形的な意味合いについて解説してみました。\(\small n\)乗根の求め方は、解き方のコツさえつかんでしまえば、いろいろな問題で応用できる非常に重要な考え方になるので、是非マスターしておきましょう!
最後に今回の重要ポイントを復習して終わりにしましょう。
☆重要ポイント☆
≫ \(\small n\)乗根の求め方
\(\small z^n =a+bi\)(\(\small n\)は自然数、\(\small a,b\)は実数)を以下の3ステップで解け!
STEP1: 左辺を\(\small z = r(\cos \theta +i\sin \theta)\)とおいてド・モアブルの定理を適用
STEP2: 右辺を極形式に変換
STEP3: 両辺の原点からの距離と偏角を比較
≫ 複素数平面上での\(\small n\)乗根の図形的意味合い
\(\small z^n =a+bi\)(\(\small n\)は自然数、\(\small a,b\)は実数)を満たす\(\small n\)乗根は、原点を中心とした正\(\small n\)角形の頂点に位置する。
今回は以上です。お疲れさまでした!






コメント