今回は媒介変数表示された曲線のグラフの概形を求める方法について徹底解説していきます。「媒介変数」と聞くと概形の把握が大変な印象を持っている人も多いと思います。また、三次関数や三角関数といった既知の関数と異なり、数式からはグラフの概形が想像しにくいという特徴もあり、5段階、7段階の増減表を書かないといけないことから、難関大学入試でも頻出の分野になっています。
そこで本記事では、入試でよく出る媒介変数表示された曲線の代表例として、サイクロイド、アステロイド、カージオイド曲線の概形の求め方についてわかりやすく解説していこうと思います。特に増減表の書き方は参考書によっても様々ですが、本記事では個人的におすすめしたい増減表の書き方についても解説していこうと思いますので、是非最後まで確認してみてください!
- 媒介変数表示された曲線の概形の求め方が知りたい人
- サイクロイド、アステロイド、カージオイド曲線の理解を深めたい人
- 媒介変数表示された曲線の増減表の書き方のコツを知りたい人
- 大学入試対策・定期テスト対策がしたい人
【問題&解説】媒介変数表示された曲線の概形
【問題1】サイクロイド曲線の概形(難易度:★☆☆)
\(\small x\)軸に接する半径\(\small r\)の円(ただし\(\small r>0\)とし、円の中心座標を \(\small \mathrm{C}(0,r)\)とする)の円周上に点\(\small \mathrm{P}(0,0)\)をとる。この円が\(\small x\)軸に接しながら正の方向に滑ることなく1回転するとき、以下の問いに答えよ。
(1)点\(\small \mathrm{C}\)から\(\small x\)軸に下した垂線と線分\(\small \mathrm{CP}\)がなす角度を\(\small \theta\)とするとき、点\(\small \mathrm{P}\)の座標を\(\small r\)および\(\small \theta\)を用いて表せ。
(2)円周上の点\(\small \mathrm{P}\)が描く曲線の概形を図示せよ。
・媒介変数表示された曲線の増減表は6段階で作成するのがおすすめ(詳細は媒介変数表示された曲線の増減表の作り方を参照)。
問題文が少々複雑だが、半径\(\small r\)、円の中心座標\(\small \mathrm{C}(0,r)\)、円周上の点\(\small \mathrm{P}\)、角度\(\small \theta\)の関係性を図示すると下図のようになる。最初は左側の円のような状態になっており、\(\small x\)軸正の方向へ回転するにつれて点\(\small \mathrm{P}\)が右図のように移動していくことがイメージできていればよいだろう。
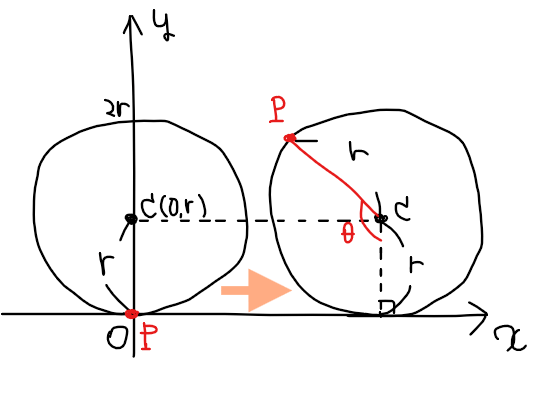
状況整理ができたところで、ここからは点\(\small \mathrm{P}\)の座標を\(\small r,\theta\)を用いて表すことを考えていく。ここで、点\(\small \mathrm{P}\)の座標は原点を始点とする\(\small \overrightarrow{\mathrm{OP}}\)のベクトルの成分に等しい([*1])ことから、\(\small \overrightarrow{\mathrm{OP}}\)の成分を求めることを考える。
*1:補足
原点を始点とするベクトルの成分表示は、終点の座標になります。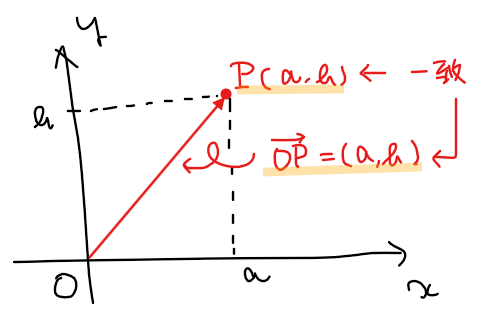
下図より、
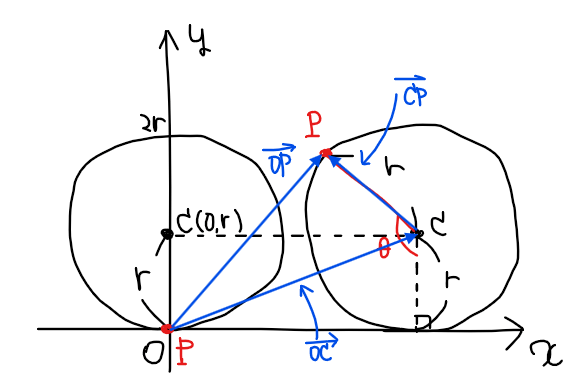
\begin{split}
\small \overrightarrow{\mathrm{OP}} &\small =\overrightarrow{\mathrm{OC}}+\overrightarrow{\mathrm{CP}}\\
&\small \displaystyle =
\begin{pmatrix}
r\theta\\ r
\end{pmatrix}
+
\begin{pmatrix}
r\cos\left(\dfrac{3}{2}\pi-\theta\right)\\ r\sin\left(\dfrac{3}{2}\pi-\theta\right)
\end{pmatrix}
\space [*2]
\\
&\small =
\begin{pmatrix}
r\theta-r\sin\theta\\ r-r\cos\theta
\end{pmatrix}\\
\end{split}
よって、点\(\small \mathrm{P}\)の座標は\(\small \mathrm{P}(r(\theta-\sin \theta),r(1-\cos\theta))\)…【答】.
\(\small *2\):補足
\(\small \overrightarrow{\mathrm{OC}}\)と\(\small \overrightarrow{\mathrm{CP}}\)の成分計算は、図形的な考察が要求されるため、慣れていないと若干躓くので補足解説。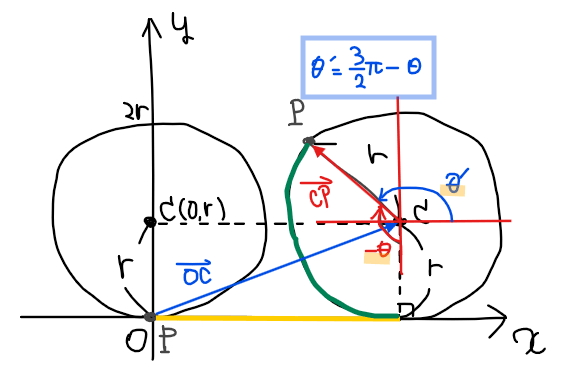
まず、\(\small \overrightarrow{\mathrm{OC}}\)については、\(\small x\)座標は上図の黄色の長さになるが、これは問題文よりもともと原点にあった点\(\small \mathrm{P}\)が回転した距離である緑色の弧の長さと等しくなる。そして緑色の長さは弧度法(ラジアン)を用いて「半径×角度[ラジアン]」で求めることができるため、\(\small \color{red}{r\theta}\)となる。
次に、\(\small \overrightarrow{\mathrm{CP}}\)については、極座標表示の考え方に立ち返り、x軸正の部分からの方向付角度(反時計回り:正、時計回り:負)と半径で機械的に座標を求めることが効果的である。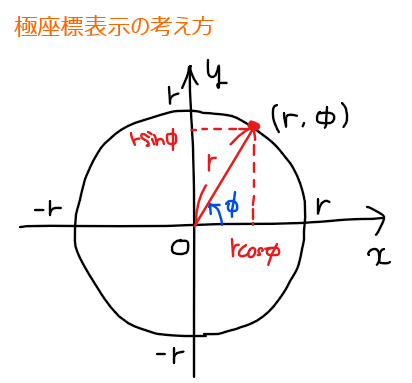
本問であれば、点\(\small \mathrm{P}\)は \(\small x\) 軸正の部分から \(\small \displaystyle \frac{3}{2}\pi-\theta\) だけ進んだ位置にいることが分かるため、極座標表示の角度\(\small \phi\)を\(\small \displaystyle \frac{3}{2}\pi-\theta\)とすることでベクトルの成分を求めることができる。このように、点\(\small \mathrm{P}\)の角度に注目して位置を考えてあげればよく、図形的な位置までは把握不要という点がポイントだ。
別解としてベクトルを用いずに図形的に求めることも可能。
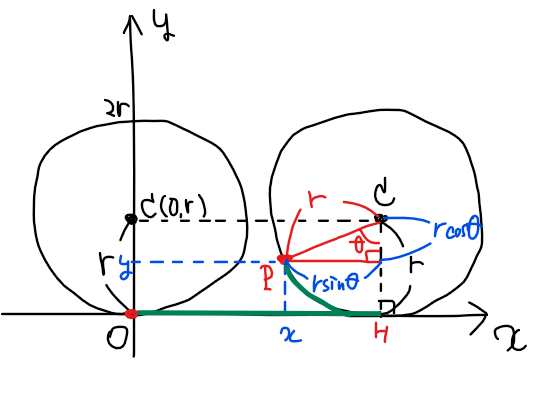
便宜上、イメージがしやすいように\(\small \theta\)が\(\small \pi/2\)以下の場合の図で考える(上図)。このとき、点\(\small \mathrm{P}\)の座標は
\begin{split}
\small x &\small =\mathrm{OH}-\color{blue}{r\sin \theta}\\
&\small =r\theta-r\sin \theta\\
&\small =r(\theta-\sin \theta)\\
\end{split}
\begin{split}
\small y &\small =r-\color{blue}{r\cos \theta}\\
&\small =r(1-\cos\theta)\\
\end{split}
よって、点\(\small \mathrm{P}\)の座標は\(\small \mathrm{P}(r(\theta-\sin \theta),r(1-\cos\theta))\)…【答】.
(1)の結果より、点\(\small \mathrm{P}\)の座標は媒介変数\(\small \theta\)を用いて
\begin{cases}
\small x =r(\theta-\sin \theta)\\
\small y=r(1-\cos\theta)\\
\end{cases}
と表される。ここで、角度\(\small \theta\)は円が回転した角度なので、1回転の範囲では\(\small 0≦\theta≦2\pi\)となることに注意されたい。
媒介変数表示されたグラフの概形を描くには、6段階の増減表を作成するのがおすすめ(作り方は媒介変数表示された曲線の増減表の作り方で解説)。増減表の作成するための準備段階として、\(\small x,y\)を媒介変数である\(\small \theta\)でそれぞれ微分し極値を確認しておく。
\(\small r\)は半径であり定数であることに注意すると
\begin{split}
\small \displaystyle \frac{dx}{d\theta}=r(1-\cos\theta)
\end{split}
より、\(\small \displaystyle \frac{dx}{d\theta}=0\)となるときの\(\small \theta\)の値は
\begin{split}
&\small r(1-\cos\theta)=0\\
\small \Leftrightarrow \space &\small \cos\theta=1\\
\small ∴ \space &\small \theta=0,2\pi\\
\end{split}
同様に、
\begin{split}
\small \displaystyle \frac{dy}{d\theta}=r\sin\theta
\end{split}
より、\(\small \displaystyle \frac{dy}{d\theta}=0\)となるときの\(\small \theta\)の値は
\begin{split}
&\small r\sin\theta=0\\
\small ∴ \space &\small \displaystyle \theta=0,\pi,2\pi\\
\end{split}
また、
\begin{split}
\small \displaystyle \frac{dy}{dx} &\small =\frac{dy/d\theta}{dx/d\theta}\\
&\small =\frac{r\sin\theta}{r(1-\cos\theta)}\\
&\small =\frac{\sin\theta(1+\cos\theta)}{(1-\cos\theta)(1+\cos\theta)}\\
&\small =\frac{(1+\cos\theta)}{\sin\theta}\\
\end{split}
より、
\begin{split}
\small \displaystyle \lim_{\theta \to +0} \frac{dy}{dx}
&\small = \lim_{\theta \to 0} \frac{(1+\cos\theta)}{\sin\theta}\\
&\small = \infty\\
\small \displaystyle \lim_{\theta \to 2\pi-0} \frac{dy}{dx}
&\small = \lim_{\theta \to 2\pi-0} \frac{(1+\cos\theta)}{\sin\theta}\\
&\small = -\infty\\
\end{split}
以上の情報から増減表は下図の通り。
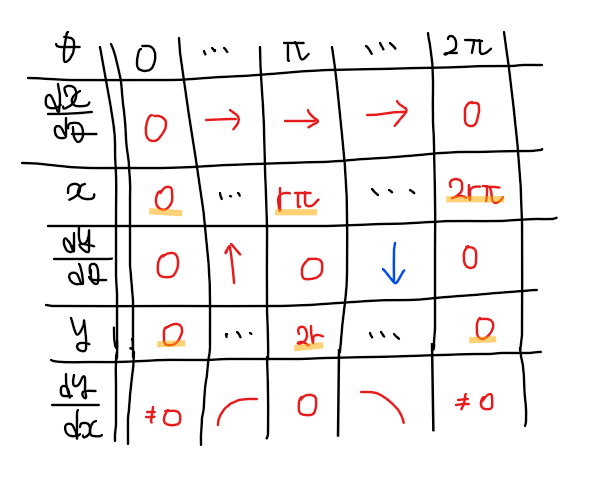
よって、グラフの概形を図示すると以下のようになる。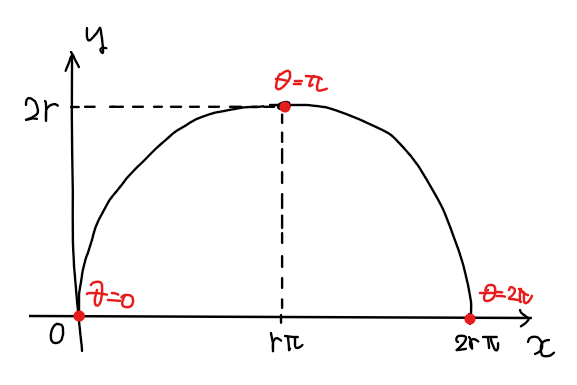 …【答】
…【答】
媒介変数表示された曲線の増減表は通常の増減表と若干異なるので、ここではおすすめの作り方を解説する。
まずは、下図のように6段階の増減表の枠を用意する。

●補足
参考書では5段階(表の上5つまで)の増減表が主流だが、グラフをしっかり描くならば個人的には\(\small dy/dx\)まで含めた6段階の増減表をかく方が概形を掴みやすいと思っている。
次に、準備段階で求めたパラメータ微分に関する極値(微分=0の箇所)を埋めていく。併せて、
$$\small \displaystyle \frac{dy}{dx}=\frac{\dfrac{dy}{d\theta}}{\dfrac{dx}{d\theta}}$$
の関係から、\(\small dy/dx\)の値も求めておく。ここが「0」か「0以外」かが概形把握では重要になってくる。
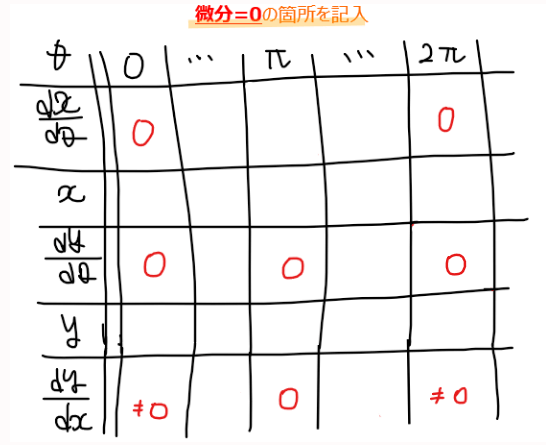
本問であれば、\(\small \theta=0,2\pi\)では\(\small dx/d\theta\)と\(\small dy/d\theta\)がともに0のため、\(\small 0/0\)(不定形)となっているので、解答のように極限が求まるように式変形が必要。
一方で、\(\small \theta=\pi\)では、\(\small dx/d\theta \neq 0\)、\(\small dy/d\theta =0\)なので、\(\small dy/dx=0\)となる。
各極値での\(\small x,y\)座標の値を埋める。座標の値を求める作業は必須ではないが、グラフの概形を描くときには\(\small x,y\)座標の値があるとグラフが通過する点が分かりやすくなり概形が把握しやすくなるので求めておくのがおすすめ。
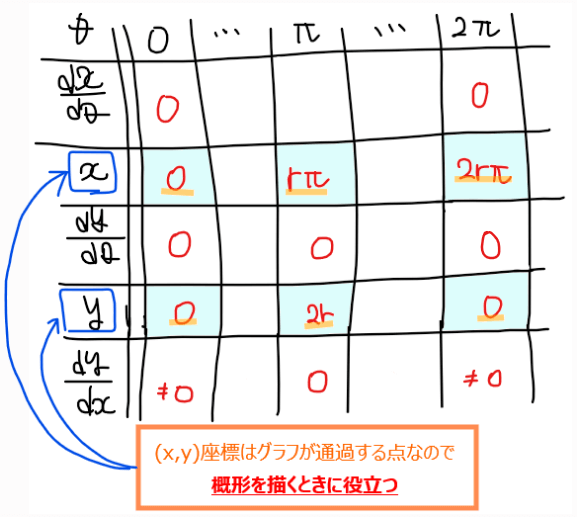
最後に、\(\small \displaystyle \frac{dx}{d\theta}、\frac{dy}{d\theta}\)の空欄箇所に矢印、\(\small \displaystyle \frac{dy}{dx}\)の空欄箇所に概形を記入していく。ここが媒介変数表示特有のポイントである。

通常の\(\small y=f(x)\)の形で表される関数の増減表であれば、\(\small \displaystyle \frac{dy}{dx}\)の1つしかないため増減が分かりやすいが、媒介変数表示の場合は、\(\small x\)方向と\(\small y\)方向それぞれの増減があるため、上図のように、\(\small \displaystyle \frac{dx}{d\theta}\)であれば\(\small x\)方向の増減、\(\small \displaystyle \frac{dy}{d\theta}\)であれば\(\small y\)方向の増減を確認したうえで、グラフの概形を確認する必要がある。
●補足
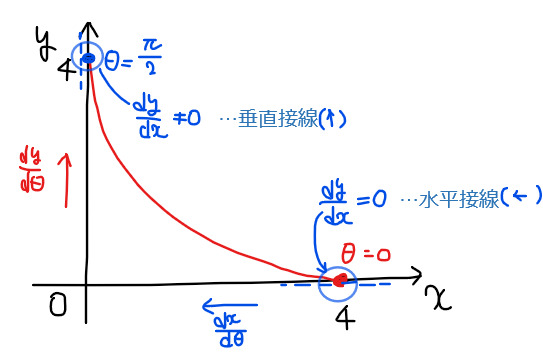
\(\small \displaystyle \frac{dx}{d\theta}\),\(\small \displaystyle \frac{dy}{d\theta}\)の符号の組合せごとのグラフの概形は下図のようになる。どちらの概形になるかは、増減表6段目で\(\small \displaystyle \frac{dy}{dx}=0\)側が水平接線、\(\small \displaystyle \frac{dy}{dx}\neq 0\)側で垂直接線になることから判断できる。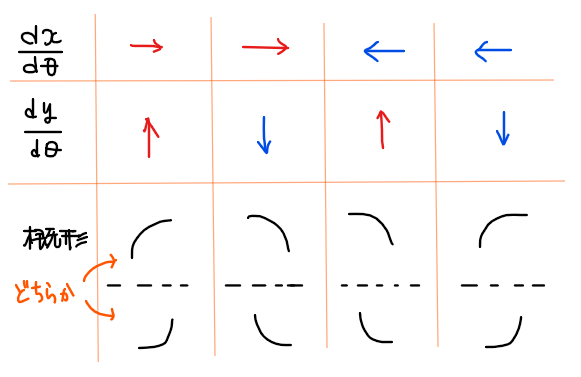
たとえば、本問であれば、\(\small 0≦\theta≦\pi\)の範囲では\(\small \theta=0\)側(左側)が\(\small \displaystyle \frac{dy}{dx}\neq 0\)なので垂直接線、\(\small \theta=\pi\)側(右側)が\(\small \displaystyle \frac{dy}{dx}=0\)なので水平接線となるので解答のようなカーブになる。
【問題2】アステロイド曲線の概形(難易度:★★☆)
\(\small xy\)平面において、原点\(\small O\)を中心とする半径4の円\(\small C\)の内側を半径1の円\(\small C^\prime\)が内接しながら滑ることなく転がるとき、円\(\small C^\prime\)上の点\(\small \mathrm{P}\)が描く曲線を\(\small X\)とする。ただし、点\(\small \mathrm{P}\)のはじめの位置は点\(\small \mathrm{P}_0(4,0)\)とする。円\(\small C^\prime\)の中心\(\small O^\prime\)が原点\(\small O\)のまわりを\(\small \theta\)だけ回転したときの点\(\small \mathrm{P}\)の座標を\(\small (x,y)\)とするとき、次の問いに答えよ。
(1)\(\small x,y\)を\(\small \theta\)を用いて表せ。
(2)曲線\(\small X\)の概形を図示せよ。
[岐阜薬科大 改題]
・(2)は図形の対称性を確認しておくと増減表を作成する範囲を絞ることができ、論証も楽になる。
・概形の凹凸は、\(\small dy/dx\)が「0」か「0以外」かで判断。
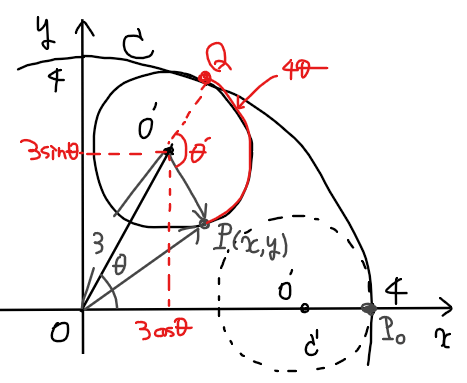
問題文から点\(\small \mathrm{P}\)を図示すると下図の通り。
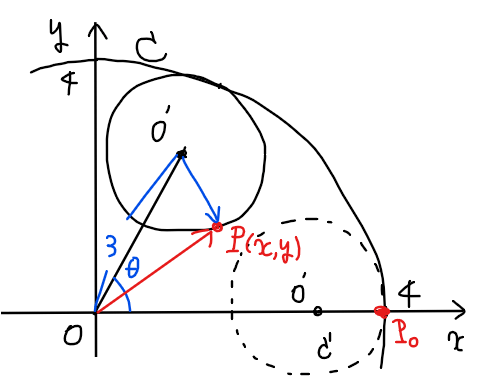
下図のように点\(\small \mathrm{Q}\)を円\(\small C\)と円\(\small ^\prime\)の接点とし、\(\small \angle PO^\prime Q=\theta^\prime\)とおく。
\(\small \stackrel{\huge\frown}{PQ}=\stackrel{\huge\frown}{P_0Q}\)(転がった距離が等しいため)であることから、
\begin{split}
&\small \stackrel{\huge\frown}{PQ}=\theta^\prime \space [*1]\\
&\small \stackrel{\huge\frown}{P_0Q}=4\theta\\
\end{split}
より、\(\small \theta^\prime =4\theta\)を得る(これは、半径が1/4なので回転角が4倍になっていることを意味する)。
*1:補足
円の半径を\(\small r\)、中心角を\(\small \theta\)(ラジアン)とする場合、その弧の長さ\(\small \ell\)は
$$\small \ell =r\theta$$
よって、
\begin{split}
\small \overrightarrow{\mathrm{OP}} &\small =\overrightarrow{\mathrm{OO^\prime}}+\overrightarrow{\mathrm{O^\prime P}}\\
&\small =
\begin{pmatrix}
3\cos \theta\\ 3\sin \theta
\end{pmatrix}
+
\begin{pmatrix}
\cos(-3\theta)\\ \sin(-3\theta)
\end{pmatrix}
\space [*2]
\\
&\small =
\begin{pmatrix}
3\cos \theta\\ 3\sin \theta
\end{pmatrix}
+
\begin{pmatrix}
\cos 3\theta\\ -\sin 3\theta
\end{pmatrix}
\\
&\small =
\begin{pmatrix}
3\cos \theta+\cos 3\theta\\ 3\sin \theta-\sin 3\theta
\end{pmatrix}
\\
&\small =
\begin{pmatrix}
4\cos^3 \theta\\ 4\sin^3 \theta
\end{pmatrix}
\space [*3]
\\
\end{split}
*2:【補足】\(\small \overrightarrow{\mathrm{O^\prime P}}\)の成分の求め方
本問の場合、図形的な位置関係から解こうとすると、正確な点\(\small \mathrm{P}\)の位置関係を把握する必要があるが、これはかなり難しい(下図参照)。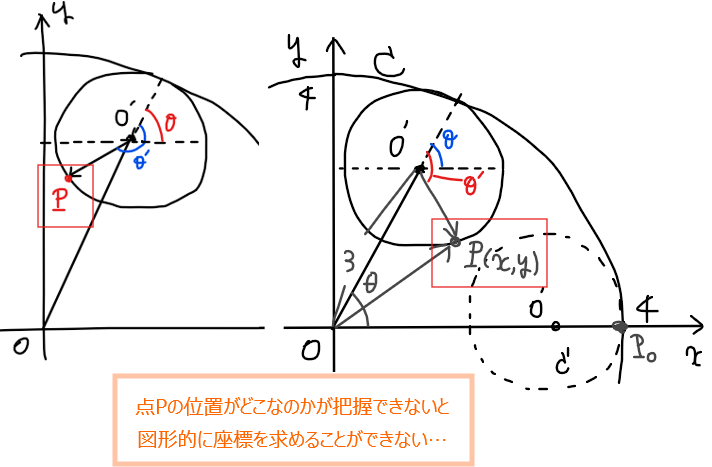
このような場合は、問題1でも解説した通り極座標表示の考え方に立ち返り、\(\small x\)軸正の部分からの方向付角度(反時計回り:正、時計回り:負)と半径で機械的に座標を求めることが効果的だった。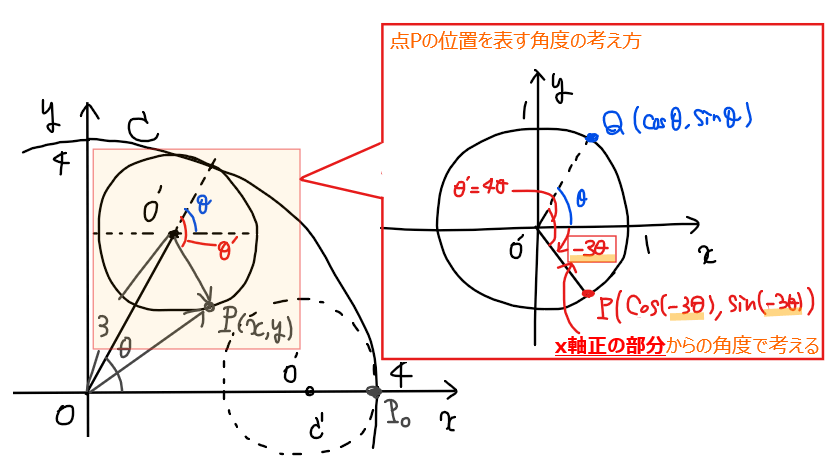
本問であれば、点\(\small \mathrm{P}\)は \(\small -3\theta\) 進んだ位置にいることが分かる。
*3:【補足】3倍角の公式
\(\small \sin 3\theta,\cos 3\theta\)の処理は、3倍角の公式を利用する。加法定理から導出できるようにしておけば公式自体は暗記不要。
\begin{split}
\small \color{#ef5350}{\sin 3\theta} &\small =\sin(\theta +2\theta)\\
&\small =\sin\theta\cos 2\theta+\cos \theta \sin 2\theta\\
&\small =\sin\theta(1-2\sin^2\theta)+2\sin \theta \cos^2 \theta\\
&\small =\sin\theta-2\sin^3\theta+2\sin \theta (1-\sin^2 \theta)\\
&\small = \color{#ef5350}{3\sin\theta-4\sin^3\theta}\\
\small \color{#ef5350}{\cos 3\theta} &\small =\cos(\theta +2\theta)\\
&\small =\cos\theta\cos 2\theta-\sin \theta \sin 2\theta\\
&\small =\cos\theta(2\cos^2\theta-1)-2\sin^2 \theta \cos \theta\\
&\small =2\cos^3\theta-\cos\theta-2\cos \theta (1-\cos^2 \theta)\\
&\small = \color{#ef5350}{4\cos^3\theta-3\cos\theta}\\
\end{split}
ゆえに、
\begin{split}
\begin{cases}
\small \color{red}{x=4\cos^3 \theta}\\
\small \color{red}{y=4\sin^3 \theta}\\
\end{cases}
\small \color{red}{\space \cdots【答】}
\end{split}
円\(\small C\)の内側を円\(\small C^\prime\)が内接しながら転がるという操作は\(\small xy\)平面の原点\(\small O\)に対して点対称であることから、\(\small x>0,y>0\)の部分、すなわち\(\small \displaystyle 0≦\theta≦\frac{\pi}{2}\)の範囲だけ考えて最後に回転させることで全体の概形を描くことができる。
\begin{split}
\small \displaystyle \frac{dx}{d\theta} &\small =-12\cos^2 \theta \sin \theta≦0\\
\end{split}
(\(\small \displaystyle 0≦\theta≦\frac{\pi}{2}\)では\(\small \sin \theta≧0\)のため)より、\(\small dx/d\theta=0\)となる\(\small \theta\)の値は\(\small \displaystyle 0≦\theta≦\frac{\pi}{2}\)であることに注意すると
\begin{split}
&\small \displaystyle \sin \theta = 0, \space \cos \theta =0\\
&\small \displaystyle ∴ \space \theta = 0, \frac{\pi}{2}\\
\end{split}
同様に
\begin{split}
\small \displaystyle \frac{dy}{d\theta} &\small =12\sin^2 \theta \cos \theta≧0\\
\end{split}
(\(\small \displaystyle 0≦\theta≦\frac{\pi}{2}\)では\(\small \cos \theta≧0\)のため)より、\(\small dy/d\theta=0\)となる\(\small \theta\)の値は
\begin{split}
&\small \displaystyle \sin \theta = 0, \space \cos \theta =0\\
&\small \displaystyle ∴ \space \theta = 0, \frac{\pi}{2}\\
\end{split}
また、
\begin{split}
\small \displaystyle \frac{dy}{dx} &\small = \frac{dy/d\theta}{dx/d\theta}\\
&\small = \frac{12\sin^2 \theta \cos \theta}{-12\cos^2 \theta \sin \theta}\\
&\small = -\frac{\sin \theta}{\cos \theta}\\
&\small = -\tan\theta\\
\end{split}
より、\(\small \theta =0\)のとき、\(\small dy/dx=0\)、
\begin{split}
&\small \displaystyle \lim_{\theta \to \frac{\pi}{2}-0} \frac{dy}{dx}\\
&\small \displaystyle = -\lim_{\theta \to \frac{\pi}{2}-0} \tan\theta\\
&\small = -\infty\\
\end{split}
以上の情報から増減表は
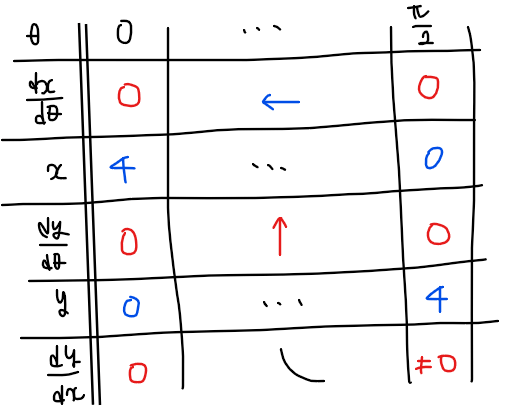
となるので、\(\small \displaystyle 0≦\theta≦\frac{\pi}{2}\)のグラフの概形は
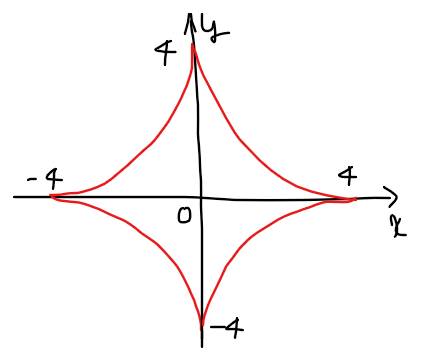
最後に、冒頭に考察したように曲線 \(\small X\)は原点\(\small O\)に関して点対称となることから、曲線 \(\small X\)の概形は下図のようになる。
【問題3】カージオイド曲線の概形(難易度:★★★)
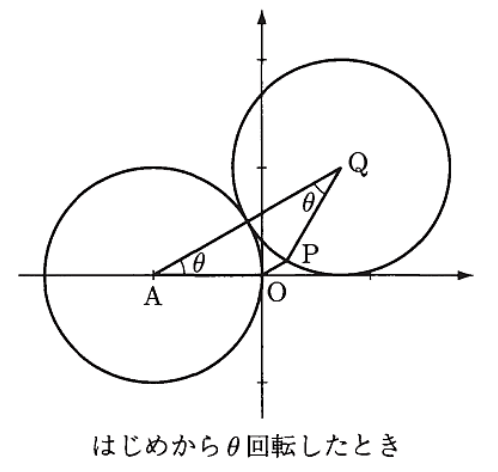
点\(\small \mathrm{A}(-1,0)\)を中心とする半径1の円\(\small A\)があり、半径1の円\(\small Q\)は円\(\small A\)に外接しながら滑ることなく反時計回りに半周する。円\(\small Q\)上の点\(\small \mathrm{P}\)ははじめ原点にある。下図は円\(\small Q\)が角\(\small \theta\)回転した状態を示す。このとき、以下の問いに答えよ。
(1)点\(\small \mathrm{P}\)の座標を\(\small \theta\)を用いて表せ。
(2)点\(\small \mathrm{P}\)が描く曲線の概形を図示せよ。
[順天堂大 改題]
・(2)は極値が多く出てくるので、丁寧に三角不等式を解いて\(\small dx/d\theta、dy/d\theta\)の符号を確認していく必要がある(三角不等式の解き方に関しては、「三角関数を含む不等式」の解説記事で詳しく説明しています)。
・\(\small dy/dx\)の計算では、\(\small \theta = 0\)のとき\(\small dy/dx = 0/0\)の不定形になっているため、適切に式変形してから極限をとる必要がある。
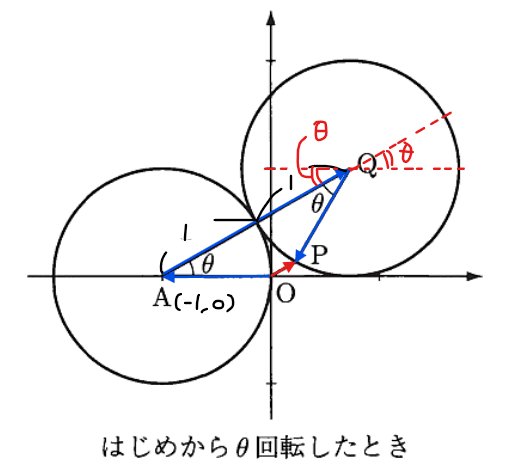
\(\small \overrightarrow{\mathrm{OP}} = \overrightarrow{\mathrm{OA}}+ \overrightarrow{\mathrm{AQ}}+ \overrightarrow{\mathrm{QP}}\)であり、
\begin{split}
&\small \overrightarrow{\mathrm{OA}}=
\begin{pmatrix}
-1\\ 0
\end{pmatrix}\\
&\small \overrightarrow{\mathrm{AQ}}=
\begin{pmatrix}
2\cos \theta\\ 2\sin \theta
\end{pmatrix} \space [*1]\\
&\small \overrightarrow{\mathrm{QP}}=
\begin{pmatrix}
\cos(\pi+2\theta)\\ \sin(\pi+2\theta)
\end{pmatrix}\\
&\small \quad =
\begin{pmatrix}
-\cos 2\theta\\ -\sin 2\theta
\end{pmatrix} \space [*2]\\
\end{split}
より、
\begin{split}
\small \overrightarrow{\mathrm{OP}} &\small =
\begin{pmatrix}
2\cos\theta-\cos 2\theta -1\\ 2\sin\theta -\sin 2\theta
\end{pmatrix}
\end{split}
よって、点\(\small \mathrm{P}\)の座標は、\(\small \mathrm{P}(2\cos\theta-\cos 2\theta -1,\space 2\sin\theta -\sin 2\theta)\)…【答】.
*1:補足
下図のような直角三角形を考えてあげれば、点\(\small \mathrm{A}\)から点\(\small \mathrm{Q}\)までは、\(\small x\)方向に\(\small 2\cos \theta\)、\(\small y\)方向に\(\small 2\sin \theta\)進むことから、解答の成分表示になる。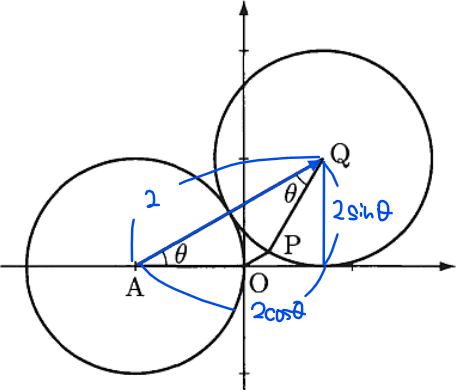
*2:【補足】\(\small \overrightarrow{\mathrm{QP}}\)の成分の求め方
極座標表示の考え方を利用して、点\(\small \mathrm{P}\)の位置を下図赤軸の\(\small x\)軸正の方向からの角度で考えると、\(\small \pi+2\theta\)(もしくは\(\small -\pi+2\theta\)でも可)なので、半径1であることから解答のような成分表示ができる。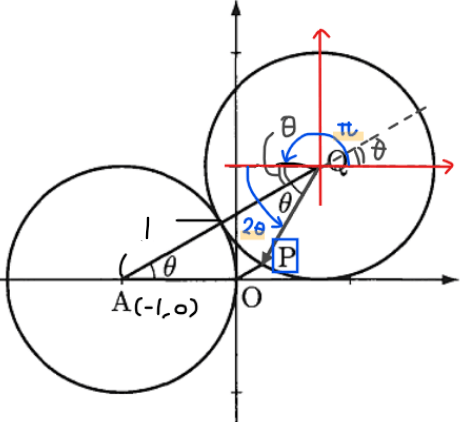
(1)の結果から、
\begin{split}
\small \displaystyle \frac{dx}{d\theta} &\small =-2\sin \theta+2\sin 2\theta\\
&\small =-2\sin \theta+4\sin \theta \cos \theta\\
&\small =2\sin\theta(2 \cos \theta-1)\\
\end{split}
円\(\small Q\)は半周だけ回転することから、角\(\small \theta \)の範囲は\(\small 0≦\theta≦\pi\)となることに注意して、\(\small dx/d\theta≧0\)となる\(\small \theta\)の範囲を求めると、
\begin{split}
&\small 2\sin\theta(2 \cos \theta-1)≧0\\
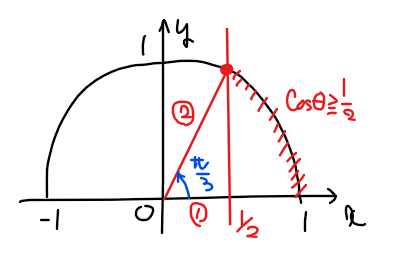
\small \Rightarrow \space &\small \sin\theta≧0, \space かつ、\cos \theta≧\frac{1}{2} \\
&\small または、\space \sin\theta≦0, \space かつ、\cos \theta≦\frac{1}{2} \space [*3]\\
& \small ∴ \space 0≦\theta≦\frac{\pi}{3}, \space \theta=\pi\\
\end{split}
*3:【補足】\(\small AB≧0\)の解き方
掛け算が0以上ということは、「\(\small (0以上)×(0以上)\)」または「\(\small (0以下)×(0以下)\)」ということなので、A、Bは以下(1)、(2)のいずれかを満たす。
(1)\(\small \mathrm{A}≧0\) かつ \(\small \mathrm{B}≧0\)
(2)\(\small \mathrm{A}≦0\) かつ \(\small \mathrm{B}≦0\)
同様に、\(\small dy/d\theta\)についても考えると
\begin{split}
\small \displaystyle \frac{dy}{d\theta} &\small =2\cos\theta-2\cos2\theta\\
&\small =2\cos\theta-2(2\cos^2\theta-1)\\
&\small =-2(2\cos^2\theta-\cos\theta-1)\\
&\small =-2(2\cos\theta+1)(\cos\theta-1)\\
\end{split}
より、\(\small dy/d\theta≧0\)となる\(\small \theta\)の範囲は
\begin{split}
&\small -2(2\cos\theta+1)(\cos\theta-1)≧0\\
\small \Leftrightarrow \space &\small (2\cos\theta+1)(\cos\theta-1)≦0\\
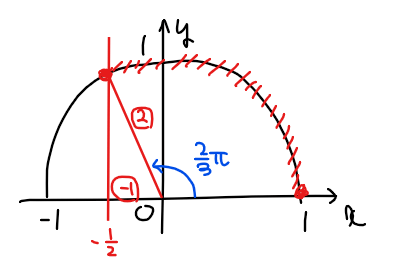
\small \Leftrightarrow \space &\small -\frac{1}{2}≦\cos \theta≦1\\
\small ∴ \space &\small 0≦\theta≦\frac{2}{3}\pi\\
\end{split}
また、
\begin{split}
\small \displaystyle \frac{dy}{dx} &\small =\frac{dy/d\theta}{dx/d\theta}\\
&\small =\frac{-2(2\cos\theta+1)(\cos\theta-1)}{2\sin\theta(2 \cos \theta-1)}\\
&\small =-\frac{(2\cos\theta+1)(\cos\theta-1)\color{#ef5350}{(\cos\theta+1)}}{\sin\theta(2 \cos \theta-1)\color{#ef5350}{(\cos\theta+1)}}\\
&\small =-\frac{(2\cos\theta+1)\cdot(\color{#ef5350}{-\sin^2\theta})}{\sin\theta(2 \cos \theta-1)(\cos\theta+1)}\\
&\small =\frac{(2\cos\theta+1)\sin\theta}{(2 \cos \theta-1)(\cos\theta+1)}\\
\end{split}
より、
\begin{split}
\small \displaystyle \lim_{\theta \to +0} \frac{dy}{dx} &\small =\lim_{\theta \to +0} \frac{(2\cos\theta+1)\sin\theta}{(2 \cos \theta-1)(\cos\theta+1)}\\
&\small =\frac{3\cdot 0}{1\cdot 2}\\
&\small =0\\
\end{split}
以上の情報から増減表を作成すると
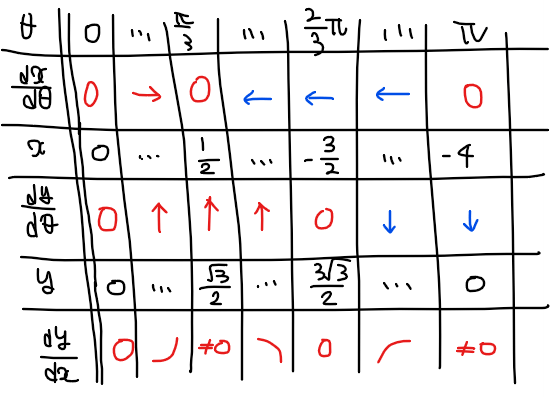
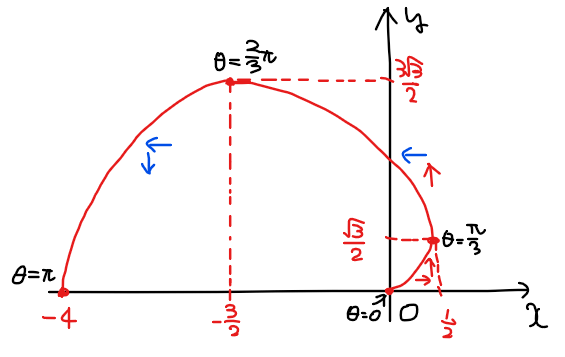
よって、グラフの概形は以下の通り。
本記事のまとめ
今回は媒介変数表示された曲線の概形の求め方について、おすすめの増減表の作り方も交えながら解説してみました。今回紹介した曲線以外の問題であっても媒介変数を含む関数のグラフの書き方は変わらないので、ぜひ他の問題にも挑戦して流れを確かめてみてください。
また、今回はグラフの概形を描く問題だったので6段階の増減表を書きましたが、たとえば、面積や回転体の体積を求めるためにおおまかな形だけ把握できればよい問題であれば、最下行までは求めずに各パラメータでの微分までを計算して5段階の増減表が書ければ十分だったりします。
概形の図示以外の問題で増減表をどのように書くかイメージしたい人は、「媒介変数表示された曲線の面積計算」の記事も併せて確認してみるといいかと思います。
では今回は以上です。お疲れさまでした!








コメント