今回は、\(\small xyz\)空間における直線や平面図形を回転させたときにできる立体の体積を求める問題について解説します。「平面図形を回転させて得られる回転体の概形や断面の形ってどうやって把握すればいいの?」という人向けに解き方のコツを分かりやすく解説しているので、ぜひ最後まで読んでみてください!
なお、本記事は、大学入試を意識した応用的なレベルになっているので、「積分を使った体積の基本問題について知りたい!」という人は、こちらの記事から読んでみることをお勧めします。
- 空間図形の回転体の問題の解き方、考え方のコツを知りたい
- 回転体の断面の形を把握するコツを知りたい
- 大学入試に向けた空間図形の回転体の体積を求める問題の演習がしたい
【座学編】問題の解き方と考え方のコツ
早速ですが、はじめに直線や平面図形の回転体の体積を求める問題の解法手順と考え方のポイントをお伝えします。
【基本方針】解法手順の大原則
■解法手順の大原則
①回転体の概形なんて考えない
②回転させる前の断面の形を把握する
「え、求める立体の形は考えないの!?」、「立体の概形が分からないと切り口の断面の形なんて分からなくない?」と驚いたり疑問に思った人もいるかもしれませんが、この方針が空間図形における回転体の大原則です。逆に言うと、多くの人がこれらを考えてしまい「どうやって概形を把握すればいいんだ…」と絶望したり、「結局、空間把握能力がない自分には捨て問だな…」とあきらめてしまうことになります。
でも実際には、概形把握は不要だし、空間把握能力なんてなくても解くことができるので、次章で具体的な解法手順について解説していきます。
【徹底解説】解法手順と考え方のポイント
では、具体的な解法手順とそれぞれのポイントを解説します。分量が多くなっていますが、まずはSTEPごとの概要だけでもいいので確認してみましょう。
【サクッと理解したい人向け】解き方解説(概要編)
■直線・平面図形の回転体の体積の求め方
・STEP1:立体を切る平面を決める
・STEP2:切断面の端点の座標を求める
・STEP3:断面図形の図示
・STEP4:切断面の面積を計算する
・STEP5:非回転体の公式で体積を求める
「5ステップもあってよくわからん!」という人は、
- 回転前の図形の断面を図示する
- その図形を回転軸まわりで回転させる
- 断面積を積分する
という流れだけまずは頭に入れておきましょう。
手順のポイントとしては、回転させた立体の断面を考えるのではなく、回転前の断面を回転させることで回転体の断面図を把握するということです。回転させたものを切るのと切ったものを回転させるのは同じなので、回転前の断面で考えた方が分かりやすいというわけです。
【詳しく理解したい人向け】解き方解説(詳細編)
立体を切る平面を決める
■切断面の決め方
回転軸と垂直な平面で切断せよ!
回転軸に垂直な平面で切ることで、断面が円形になり計算が楽になります。
(補足)
実際の入試問題では問題文の中で「平面\(\small z=t\)…」のような文言が出てくることが多いので、その場合はこの平面に沿って立体を切断すればokです。他にも問題文の中で座標の値を変数でおく指定がある場合は、その平面で切断しましょう。たとえば、「\(\small x\)座標を\(\small t\)として…」とあれば、平面\(\small x=t\)を考える感じです。
切断面の端点の座標を求める
■端点の座標を求めるコツ
空間図形における座標の値はベクトルを利用せよ!
大原則でも述べましたが、ここでは回転前の図形と切断平面との交点の座標を求めていきます(回転後の図形の切断面ではないので注意!)。
(補足)
平面図形までであれば図形的に計算して座標を求めればよかったですが、\(\small xyz\)空間では図形的に解く方法はおすすめしません。理由は、図示するのが難しいため勘違いによるミスが起きたり、時間もかかってしまうためです。
詳しくは例題で解説しますが、ベクトルを利用すれば簡単かつスピーディーに座標を求めることができます!
断面図形の図示
■断面図形を図示するコツ
断面図は必ず平面上で考えるべし!(\(\small xyz\)空間上で考えないこと)
切断面の面積を計算する
STEP3で図示した切断面を回転軸まわりで回転させることで求める断面積を計算します。
■断面把握のコツ
回転軸と回転させる図形の長軸と短軸に注目せよ!
【直線の回転】
・断面の形は円になる
└半径:断面点と回転軸との距離
・面積の求め方
(円で囲まれた立体の断面積)=\(\small \pi \times ( \color{red}{\textbf{点と回転軸との距離}})^2\)
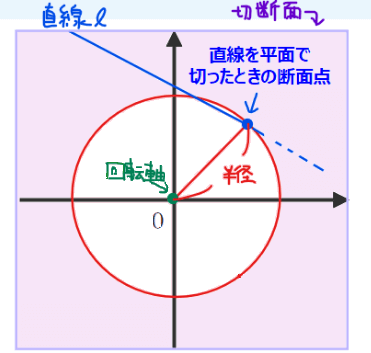
その断面は点になる。点を回すと円になる。
【平面図形の回転】
・断面の形はドーナツ型になる
└長軸:回転軸から最も遠い線分上の点との距離
└短軸:回転軸から最も近い線分上の点との距離
・面積の求め方
(通過領域の断面積)=\(\small \pi(\color{red}{\textbf{長軸}})^2-\pi (\color{blue}{\textbf{短軸}})^2\)
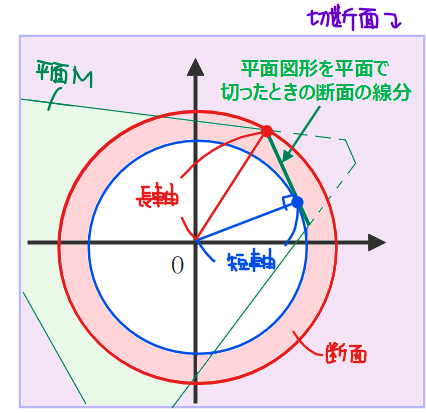
その断面は線分になる。線分を回転させたときの
通過領域はドーナツ型になる。
(補足)なんで線分を回転させるとドーナツ型になるの?
線分は、たくさんの点が集まってできています。そのため、「線分を回転させる」=「1つ1つの点を回転させる」ということになります。その結果、回転軸から最も遠い点が外円、最も近い点が内円となり、結果ドーナツ型になるわけです。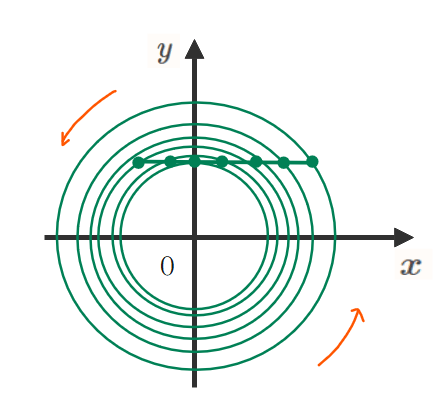
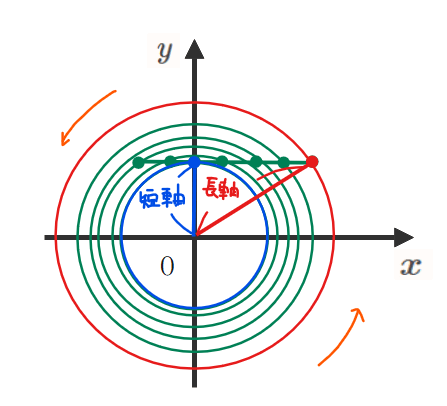
非回転体の公式で体積を求める
■非回転体の体積を求める公式
求める立体の断面積を\(\small S(t)\)として、\(\small t\)軸に沿って積み重ねる場合、その立体の体積\(\small V\)は、
$$\color{red}{V=\int S(t) dt}$$
※\(\small t\)軸(積分の軸)は、切り口の断面に垂直になるようにとる
非回転体の体積を求める公式について、詳細説明は割愛するので、詳しく知りたい人は以下の記事を確認してみてください!
【例題編】解法手順を使った問題の解き方
では、例題を通して解法手順を実際の問題でどのように使えばいいのか見ていきましょう。
\(\small xyz\)空間内の2点 \(\small \mathrm{A}(0,2,0)\), \(\small \mathrm{B}(1,0,2)\)を通る直線 \(\small \ell\)を\(\small x\)軸まわりに1回転して得られる図形と2つの平面 \(\small x=0, x=1\)で囲まれた立体の体積を求めよ。 [類 北海道大]
立体を切る平面を決める
回転軸である\(\small x\)軸と垂直な平面 \(\small x=t \)で切っていきます。問題より、今回考える立体は2つの平面 \(\small x=0, x=1\)で囲まれた立体なので、\(\small t\)の範囲は\(\small 0≦t≦1\)としておきます。
切断面の端点の座標を求める
直線 \(\small \ell\)を図示すると下図のようになります。
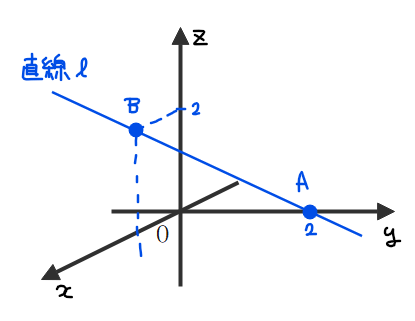
では、この直線\(\small \ell \)を\(\small x=t\)で切断したときの座標を求めています。直線と平面がの交点は1つの点になるので、直線 \(\small \ell\)と平面\(\small x=t\)との交点の座標を\(\small \mathrm{P}\)とおくことにします。
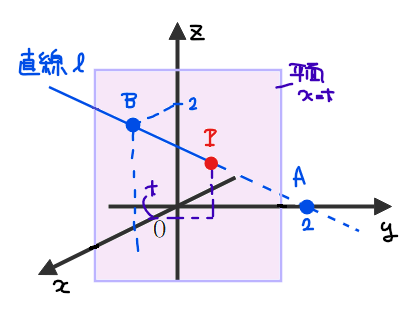
点\(\small \mathrm{P}\)の座標を求めたいのですが、空間図形の座標は図形的に考えると大変なので、ベクトルを利用します。ベクトルと座標を結びつけるにはベクトルの成分表示を使います。
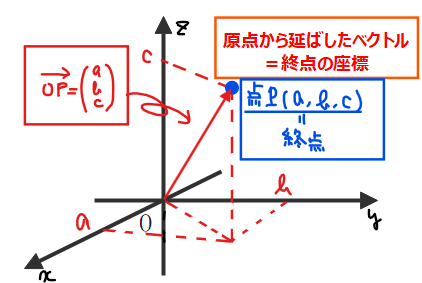
終点の座標を表す
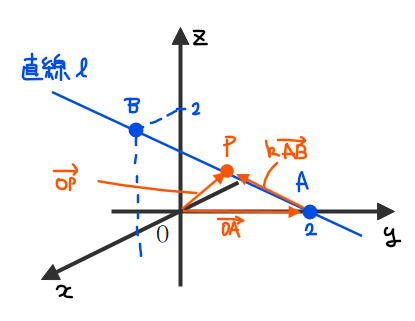
原点を始点としたベクトルの成分表示は、終点の座標を表すので、点\(\small \mathrm{P}\)の座標が知りたければ、\(\small \overrightarrow{\mathrm{OP}}\)の成分を求めればいいことになります。
下図より、\(\small \overrightarrow{\mathrm{OP}}=\overrightarrow{\mathrm{OA}}+k \overrightarrow{\mathrm{AB}}\)(ただし、\(\small k\)は実数)と表せるので、
\begin{equation}
\begin{split}
\overrightarrow{\mathrm{OP}}&=\overrightarrow{\mathrm{OA}}+k(\overrightarrow{\mathrm{OB}}-\overrightarrow{\mathrm{OA}})\\
&=(1-k)\color{red}{\overrightarrow{\mathrm{OA}}}+k\color{blue}{ \overrightarrow{\mathrm{OB}}}\\
&=(1-k)\color{red}{
\begin{pmatrix}
0\\ 2\\ 0
\end{pmatrix}}
+k\color{blue}{
\begin{pmatrix}
1\\ 0\\ 2
\end{pmatrix}}\\
&=\begin{pmatrix}
k\\ 2-2k\\ 2k
\end{pmatrix}\\
\end{split}
\end{equation}
赤字と青字の箇所は、それぞれ\(\small \mathrm{A}\)座標、\(\small \mathrm{B}\)座標の成分を代入しています。
(補足)ベクトルの成分表示の表記について
括弧の向きは高校数学では横書きだと思いますが、数学界ではベクトル成分は縦書きがスタンダードなので、本サイトでは縦書きしてます(見やすいし)。もちろん横書きでもokです。上から順に\(\small x,y,z\)座標の成分です。
今回知りたい座標\(\small \mathrm{P}\)は\(\small x\)座標が\(\small t\)なので(\(\small x=t\)との交点なので…)、\(\small k=t\)としてあげれば点\(\small \mathrm{P}\)の座標は、\(\small \mathrm{P}(t,2-2t,2t)\)と求まりました。
断面図形の図示
点\(\small \mathrm{P}\)を\(\small x\)軸まわりに回転させると下図のような円になるので、求める立体の断面はこの円の内部となります。
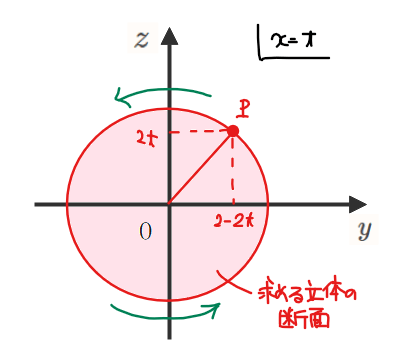
切断面の面積を計算する
断面の形状が円だとわかったので、半径\(\small \mathrm{OP}\)を求めることで面積が計算できます。三平方の定理から、\(\small \mathrm{OP}^2=(2-2t)^2+(2t)^2=4(1-t)^2+4t^2\)より、断面積を\(\small S(t)\)とおくと、\(\small \color{red}{S(t)=\pi \mathrm{OP}^2=\pi \{(4(1-t)^2+4t^2\}}\)となります。
非回転体の公式で体積を求める
最後は求めた断面積をSTEP1で設定した\(\small 0≦t≦1\)の範囲で積分すればOKです。
\begin{equation}
\begin{split}
V&=\int S(t)dt\\
&=\int_0^1 \color{red}{\pi \{(4(1-t)^2+4t^2\}} dt\\
&=4\pi \int_0^1 (1-t)^2 dt+4\pi \int_0^1 t^2 dt\\
&=4\pi \bigg[ -\frac{(1-t)^3}{3}\bigg]_0^1+4\pi \bigg[ \frac{t^3}{3} \bigg]_0^1\\
&=4\pi \bigg[ 0-\left(-\frac{1}{3} \right) \bigg]+4\pi \bigg[\frac{1}{3}-0\bigg]\\
&=\color{red}{\frac{8}{3}\pi \quad \cdots (答)}\\
\end{split}
\end{equation}
(解答)
\(\displaystyle \quad \color{red}{\frac{8}{3}\pi}\)
【実践編】問題&解説
ここからは実践編です。実際の入試問題が解けるか確認してみましょう。
【問題1】平面図形の回転体の体積
\(\small xyz\)空間に3点\(\small \mathrm{P}(1,1,0), \mathrm{Q}(-1,1,0), \mathrm{R}(-1,1,2)\)をとる。この△\(\small \mathrm{PQR}\)を\(\small z\)軸まわりに回転して得られる回転体の体積を求めよ。 [類 神戸大]
まずは△\(\small \mathrm{PQR}\)を構成する3点の位置関係を把握します。図示するとこんな感じですね。
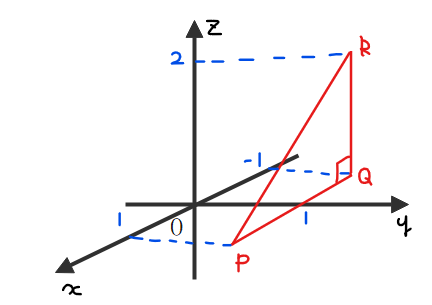
ポイントとしては、△\(\small \mathrm{PQR}\)は\(\small xz\)平面に平行であり、点\(\small \mathrm{Q}\)の真上に点\(\small \mathrm{R}\)があるということが図から読み取れればOKです。
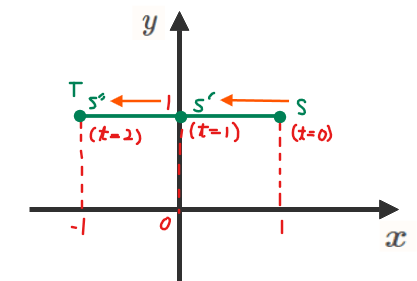
この問題では、\(\small z\)軸まわりに回転させることから、平面\(\small z=t\)(ただし、\(\small 0≦t≦2\))での断面を考えていきます。\(\small t\)の範囲は、\(\small z\)軸方向に最も長い線分\(\small \mathrm{QR}\)の範囲になります。平面\(\small z=t\)と△\(\small \mathrm{PQR}\)が交わる部分は下図のような線分(緑線箇所)になる(平面図形を平面で切った断面は線分になる)ので、端点を\(\small \mathrm{S}, \mathrm{T}\)としておきます。
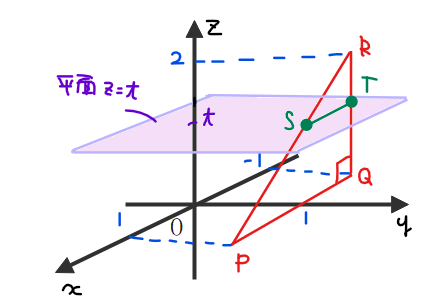
点\(\small \mathrm{S}\)の座標は、\(\small \overrightarrow{\mathrm{OS}}=\overrightarrow{\mathrm{OP}}+u\overrightarrow{\mathrm{PR}}\)(ただし、\(\small u\)は実数)より
\begin{equation}
\begin{split}
\overrightarrow{\mathrm{OS}}&=
\begin{pmatrix}
1\\ 1\\ 0
\end{pmatrix}
+u
\begin{pmatrix}
-2\\ 0\\ 2
\end{pmatrix}\\
&=
\begin{pmatrix}
1-2u\\ 1\\ 2u
\end{pmatrix}\\
\end{split}
\end{equation}
点\(\small \mathrm{S}\)の\(\small z\)座標が\(\small t\)なので、\(\small 2u=t\)、つまり\(\small u=\dfrac{t}{2}\)を上式の結果に代入することで、\(\small \mathrm{S}(1-t,1,t)\)。
同様に、点\(\small \mathrm{T}\)の座標は、\(\small \overrightarrow{\mathrm{OT}}=\overrightarrow{\mathrm{OQ}}+v\overrightarrow{\mathrm{QR}}\)(ただし、\(\small v\)は実数)より
\begin{equation}
\begin{split}
\overrightarrow{\mathrm{OT}}&=
\begin{pmatrix}
-1\\ 1\\ 0
\end{pmatrix}
+v
\begin{pmatrix}
0\\ 0\\ 2
\end{pmatrix}\\
&=
\begin{pmatrix}
-1\\ 1\\ 2v
\end{pmatrix}\\
\end{split}
\end{equation}
よって、\(\small \mathrm{T}(-1,1,t)\)。
これらの結果から、\(\small z=t\)での断面の線分点\(\small \mathrm{ST}\)を図示すると下図(\(\small z\)軸正の方向から見下ろした図)になります。
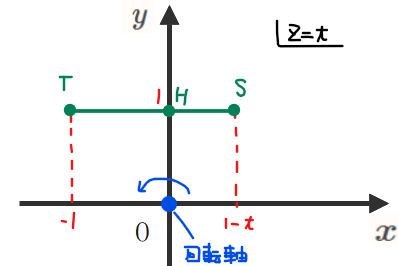
ここからは、上図の線分\(\small \mathrm{ST}\)を回転させたときの断面積を計算していきます。断面把握にあたっては、解説手順にも書いた通り、線分を回転させたときの通過領域はドーナツ型になるため、回転軸と線分の長軸と短軸に注目するというポイントを思い出しておきましょう。
■断面把握のコツ(再掲)
回転軸と回転させる図形の長軸と短軸に注目せよ!
【平面図形の回転】
・断面の形はドーナツ型になる
└長軸:回転軸から最も遠い線分上の点との距離
└短軸:回転軸から最も近い線分上の点との距離
・面積の求め方
(通過領域の断面積)=\(\small \pi(\color{red}{\textbf{長軸}})^2-\pi (\color{blue}{\textbf{短軸}})^2\)
※大きな円から小さな円を引き算した面積

図を見ると、短軸は線分\(\small \mathrm{OH}\)、長軸は線分\(\small \mathrm{OT}\)のように見えますが、点\(\small \mathrm{S}\)の\(\small x\)座標は\(\small 1-t\)なので、\(\small t\)の値によって位置が変わります。具体的に調べると、\(\small t=0\)のときは\(\small \mathrm{S}(\color{red}1,1,\color{red}0)\)、\(\small t=1\)のときは\(\small \mathrm{S}(\color{red}0,1,\color{red}1)\)、\(\small t=2\)のときは\(\small \mathrm{S}(\color{red}{-1},1,\color{red}2)\)のように、点\(\small \mathrm{S}\)は\(\small t\)の値が大きくなるにつれて点\(\small \mathrm{T}\)の方に近づいています(点\(\small \mathrm{S}\)が三角形の斜辺\(\small \mathrm{PR}\)上の点であることからもそのことが分かりますね)。
このことから、長軸は点\(\small \mathrm{S}\)がどんな位置にあるときでも線分\(\small \mathrm{OT}=\sqrt{2}\)になりそうです。
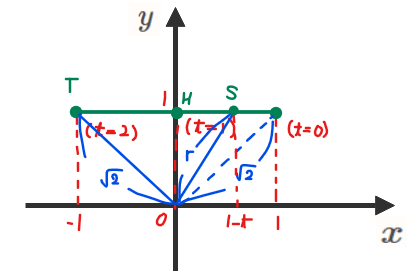
数学的に論証するなら、\(\small \mathrm{OT}^2-\mathrm{OS}^2≧0\)(2乗した差が0以上であれば\(\small \mathrm{OT}\)の方が長いことになる)を示してあげればよいので
\begin{equation}
\begin{split}
\mathrm{OT}^2-\mathrm{OS}^2&=(\sqrt{2})^2-\{(1-t)^2+1\}\\
&=2-(2-2t+t^2)\\
&=2t-t^2\\
&=t(2-t)\color{red}{≧0}\\
\end{split}
\end{equation}
なぜならば、\(\small 0≦t≦2\)のため、という論証をしておけばよいでしょう。
短軸については、一見すると原点と線分との距離が最短となる線分\(\small \mathrm{OH}\)のように思えます。ですが、下左図のような場合はそもそも交点\(\small \mathrm{H}\)がないため短軸は線分\(\small \mathrm{OS}\)になることに注意しましょう。
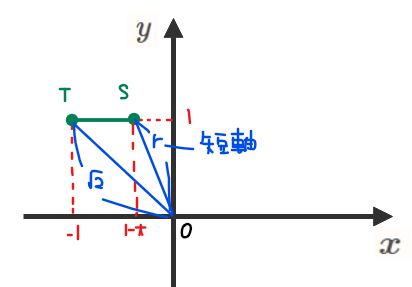
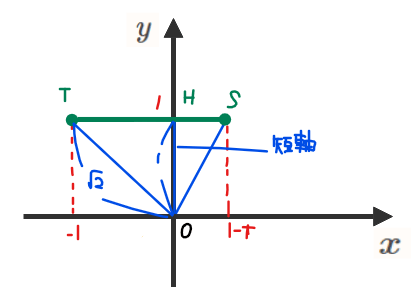
交点\(\small \mathrm{H}\)がなくなるのは、点\(\small \mathrm{S}\)の\(\small x\)座標が0以下になるときなので、\(\small 1-t≦0\)、すなわち\(\small 1≦t\)のときです。もともと\(\small 0≦t≦2\)であることから、\(\small \color{blue}{1≦t≦2}\)のとき(左上図)、短軸は線分\(\small \color{blue}{\mathrm{OS}}=\sqrt{(1-t)^2+1^2}=\color{blue}{\sqrt{2-2t+t^2}}\)、逆に\(\small \color{blue}{0≦t≦1}\)のとき(右上図)は、短軸は線分\(\small \color{blue}{\mathrm{OH}=1}\)となります。
ちょっと情報が複雑になってきたので、\(\small t\)の値ごとの長軸と短軸について整理すると以下のようになります。
[1] \(\small 0≦t≦1\)のとき
・長軸:\(\small \mathrm{OT}=\sqrt{2}\)
・短軸:\(\small \mathrm{OH}=1\)
[2] \(\small 1≦t≦2\)のとき
・長軸:\(\small \mathrm{OT}=\sqrt{2}\)
・短軸:\(\small \mathrm{OS}=\sqrt{2-2t+t^2}\)
あとは、それぞれの場合で断面積を求めていきます。断面積を\(\small S(t)\)とすると、
\(\small 0≦t≦1\)のとき、\(\small S(t)=\pi \times (\sqrt{2})^2-\pi \times 1^2=\pi\)
\(\small 1≦t≦2\)のとき、\(\small S(t)=\pi \times (\sqrt{2})^2-\pi \times (\sqrt{2-2t+t^2})^2=(2t-t^2)\pi\)
となります。
よって、求める体積\(\small V\)は
\begin{equation}
\begin{split}
V&=\int_0^2 S(t)dt\\
&=\int_0^1 \pi \space dt + \int_1^2 (2t-t^2)\pi \space dt\\
&=\pi + \pi \bigg[ t^2-\frac{t^3}{3}\bigg]_1^2\\
&=\pi + \pi \bigg[ \left( 4-\frac{8}{3}\right)-\left( 1-\frac{1}{3}\right) \bigg]\\
&=\color{red}{\frac{5}{3}\pi \quad \cdots(答)}
\end{split}
\end{equation}
(解答)
\( \displaystyle \quad \color{red}{\frac{5}{3}\pi}\)
【問題2】曲面の回転体の体積
\(\small xyz\)空間内に2点\(\small \mathrm{P}(u,u,0), \mathrm{Q}(u,0,\sqrt{1-u^2})\)を考える。\(\small u\)が0から1まで動くとき、線分\(\small \mathrm{PQ}\)が通過してできる曲面を\(\small x\)軸まわりに1回転させて得られる立体の体積を求めよ。 [類 東北大]
解法手順の5つのステップを意識して解答を読んでみると流れが分かりやすいかと思います。
\(\small x=u\)での断面図を考える。線分\(\small \mathrm{PQ}\)を図示すると下図の通り。\(\small u\)が0から1を動くとき、点\(\small \mathrm{P}\)、\(\small \mathrm{Q}\)の\(\small x\)座標も0から1へ動き、点\(\small \mathrm{P}\)の\(\small y\)座標も0から1へ動く。点\(\small \mathrm{Q}\)の\(\small z\)座標だけは1から0へ動く(緑矢印で記載)。
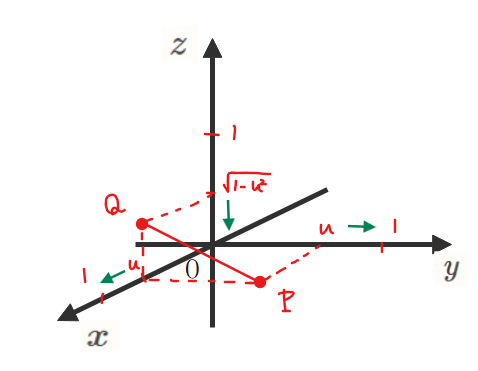
線分\(\small \mathrm{PQ}\)は\(\small yz\)平面に平行(=\(\small x\)軸に垂直)なので、\(\small x=u\)での切り口は線分\(\small \mathrm{PQ}\)そのものとなる。
(補足)
一般には線分(直線)を平面で切断すると点になりますが、今回は切断面と線分が同じ向きなので線分になっています。点の位置を図示するときには、点同士の位置関係や軸との位置関係を意識するとよいでしょう。
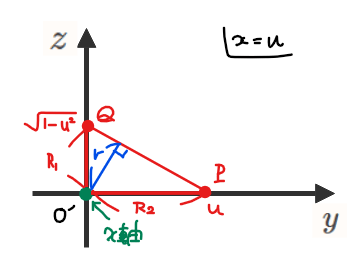
回転軸と線分\(\small \mathrm{PQ}\)との最短距離は、上図の\(\small \color{blue}r\)(点と線の距離)となるので
\begin{equation}
\begin{split}
\mathrm{△O’PQ}\mathbf{の面積}=\frac{1}{2}u(\sqrt{1-u^2})=\frac{1}{2}\mathrm{PQ}\times r\\
\end{split}
\end{equation}
であること、\(\small \mathrm{PQ}=\sqrt{u^2+(\sqrt{1-u^2})^2}=1\)であることから、\(\small \color{blue}{r=u\sqrt{1-u^2}\cdots ①}\)。
(補足)\(\small r\)の求め方
解答では、点\(\small \mathrm{O’}\)と線分\(\small \mathrm{PQ}\)との距離\(\small r\)を直角三角形\(\small \mathrm{△O’PQ}\)の面積を2通りで表すことで求めています。1つは底辺を\(\small \mathrm{O’P}\)として面積を表した中央の式、もう1つは底辺を\(\small \mathrm{PQ}\)として面積を表した右辺の式です。他にも点と直線の距離の公式を使って求めてもよいかと思います。
回転軸と線分\(\small \mathrm{PQ}\)との距離が最も長くなるのは\(\small R_1=\sqrt{1-u^2}\) または \(\small R_2=u\)だが、\(\small u\)の値によってどちらが長くなるかは異なるので場合分けして考える。
[1]\(\small R_1≧R_2\)の場合
\(\small \sqrt{1-u^2}≧u\)の場合なので、両辺とも非負であることから、両辺を2乗して不等式を解くと
\begin{equation}
\begin{split}
(1-u^2)&≧u^2\\
2u^2&≦1\\
u^2&≦\frac{1}{2}\\
-\frac{1}{\sqrt{2}}≦u&≦\frac{1}{\sqrt{2}}\\
\end{split}
\end{equation}
問題文から\(\small 0≦u≦1\)なので、共通範囲を考えることで\(\small \displaystyle \color{red}{0≦u≦\frac{1}{\sqrt{2}}}\)のとき、\(\small R_1\)の方が長くなる。
(補足)\(\small \sqrt{1-u^2}≧u\)を解く際の注意点
両辺を2乗する前に、「両辺とも非負である」という一文を入れているのは、もし仮にどちらかが負である場合2乗することで大小関係が逆転してしまう可能性があるからです。たとえば、\(\small 3≧-4\)という不等式は両辺を2乗すると\(\small 9≧16\)となり不等号が成立しなくなります。このように、不等式を2乗する際にはお互いが非負(つまりマイナスではない)であることを確認するようにしましょう。
[2]\(\small R_1≦R_2\)の場合
[1]以外の場合なので、\(\small \displaystyle \color{red}{\frac{1}{\sqrt{2}}≦u≦1}\)のとき、\(\small R_2\)の方が長くなる。
よって、\(\small x=u\)での断面積を\(\small S(u)\)とすると、
\begin{equation}
S(u)=
\begin{cases}
\pi (R_1)^2-\pi r^2 & \left(\small 0≦u≦\frac{1}{\sqrt{2}}\right)\\
\pi (R_2)^2-\pi r^2 & \left(\small \frac{1}{\sqrt{2}}≦u≦1\right)
\end{cases}
\end{equation}
①で求めた \(\small r=u\sqrt{1-u^2}\)と\(\small R_1=\sqrt{1-u^2}\)、\(\small R_2=u\)を代入することで
\begin{equation}
S(u)=
\begin{cases}
\pi(1-u^2)-\pi u^2(1-u^2) \\
=\color{red}{\pi(1-u^2)^2} & \left(\small 0≦u≦\frac{1}{\sqrt{2}}\right)\\
\pi u^2-\pi u^2(1-u^2) \\
=\color{red}{\pi u^4} & \left(\small \frac{1}{\sqrt{2}}≦u≦1\right)
\end{cases}
\end{equation}
以上より、求める立体の体積を\(\small V\)とすると
\begin{equation}
\begin{split}
V&=\int_0^1 S(u) du\\
&=\int_0^{\frac{1}{\sqrt{2}}} \pi(1-u^2)^2 du+\int_{\frac{1}{\sqrt{2}}}^1 \pi u^4 du\\
&=\pi \int_0^{\frac{1}{\sqrt{2}}} (1-2u^2) du+\color{blue}{\pi \int_0^{\frac{1}{\sqrt{2}}} u^4 du+\pi \int_{\frac{1}{\sqrt{2}}}^1 u^4 du}\\
&=\pi \int_0^{\frac{1}{\sqrt{2}}} (1-2u^2) du+\color{blue}{\pi \int_0^1 u^4 du}\\
&=\pi \bigg[ u-\frac{2}{3}u^3\bigg]_0^{\frac{1}{\sqrt{2}}}+\pi \bigg[ \frac{u^5}{5}\bigg]_0^1 \\
&=\pi\left( \frac{1}{\sqrt{2}}-\frac{2}{3}\cdot\frac{1}{2\sqrt{2}}\right)+\frac{1}{5}\pi\\
&=\color{red}{\left( \frac{\sqrt{2}}{3}+\frac{1}{5}\right)\pi \quad \cdots (答)}
\end{split}
\end{equation}
(補足)
青色の積分は以下の性質を使ってまとめてます。
$$\int_{\color{red}a}^c f(x)dx+\int_c^{\color{red}b} f(x)dx = \int_{\color{red}a}^{\color{red}b} f(x)dx$$
(解答)
\(\displaystyle \color{red}{\left( \frac{\sqrt{2}}{3}+\frac{1}{5}\right)\pi }\)
本記事のまとめ
今回は、直線や平面図形を回転させたときの体積を求める問題について解説しました。空間図形の体積が苦手という人は、まずは大原則である「回転体の概形なんて考えない」、「回転させる前の断面の形を把握する」をしっかり頭に叩き込んじゃいましょう。それだけで、問題の見方がだいぶ変わってくると思います。
そのうえで、具体的な解き方のポイントは以下5点でした。
■直線・平面図形の回転体の体積の求め方
・STEP1:立体を切る平面を決める
・STEP2:切断面の端点の座標を求める
・STEP3:断面図形の図示
・STEP4:切断面の面積を計算する
・STEP5:非回転体の公式で体積を求める
それぞれのステップごとにもポイントがあったので苦手な部分があれば再度見返して復習しておきましょう。空間図形における回転体の問題は体積計算の問題の中で最も難しい分野に位置するので、この問題がしっかり解けた人は自信をもっていいと思います。また、まだ苦手意識がある人もポイントを理解して解けるようになれば他の人と差をつけられる分野なので、ぜひあきらめずに復習してみてください。
それでは今回はここまでです。お疲れさまでした!









コメント
今まで見たどんな解説よりも分かりやすかったです!!!助かりました