今回は、\(\small y=x\)軸まわりの回転体(斜軸回転体)の体積やドーナツ型をした回転体の体積の求め方について解説します。「回転軸が斜めになったときの体積の求め方が分からない…」、「途中で出てくる置換積分の計算が苦手…」といった悩みを抱えている人向けに、斜軸回転体の立式方法と解き方のコツ、またドーナツ型の体積の計算方法についてわかりやすく解説していきます!ぜひ最後まで読んでもらって苦手を克服していきましょう!
- 斜軸回転体の体積ってどうやって立式すればいいの?
- 斜軸回転体の体積を求めるときに出てくる置換積分の方法が知りたい!
- ドーナツ型の体積ってどう求めるの?簡単に求められる裏ワザってないの?
【はじめに】回転体の体積の求め方と立式手順
斜軸回転体の問題を解く前に、回転体の体積を計算するときに知っておいてほしい前提知識を冒頭説明します。詳しくは、別記事の「回転体の体積の求め方を徹底解説(x軸、y軸まわり、バームクーヘン型積分)」で解説しているので詳細を知りたい人はこちらの記事も併せてチェックしてみてください。
ポイントだけ抜粋すると、皆さんがよく知っている回転体の体積を求める公式、\(\small \color{red}{V=\int_{a}^{b} \pi \{f(x)\}^2 dx}\)は\(\small x\)軸を軸として回した場合のみ使える公式なので、\(\small y\)軸まわりや直線\(\small y=x\)のような斜軸まわりの回転体の体積を求めるときには使うことができない公式でした。
なので、\(\small x\)軸まわり以外の回転体の体積を求める場合は、以下の公式と手順で解いていくことがポイントになります。
■回転体の体積を求める公式
回転軸からの距離(半径)を\(\small R(t)\)、回転軸を\(\small t\)軸とし、\(\small t=a\)から\(\small t=b\)まで積み上げるとき、回転体の体積\(\small V\)は
$$V=\int_{a}^b \pi \{R(t)\}^2 dt$$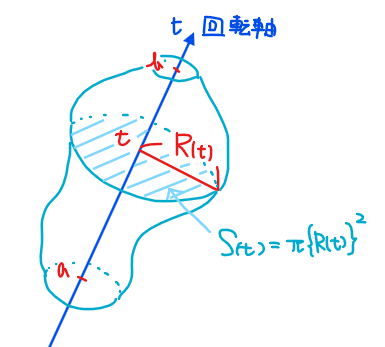
■立式の手順
①回転軸を確認する
②回転軸を積分変数として(上記なら \(\small t\))、始点と終点を積分範囲とする
③断面の半径を積分変数 \(\small t\)の関数 \(\small R(t)\)として表す
それでは、実際の問題を通して解き方を学んでいきましょう!
【問題&解説】回転体の体積計算
【問題1】斜軸回転体の体積
\(\small y=-x^2+2x\)と直線\(\small y=x\)軸で囲まれた領域を\(\small y=x\)を軸に一回転させた回転体の体積を求めよ。
問題文の領域を図示すると下図の青線部分になります。
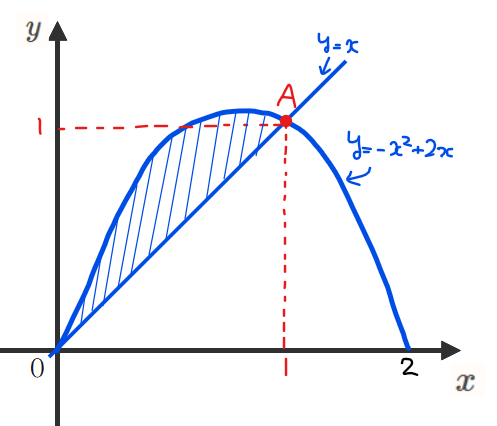
「ここから何をすればいいの?」と手が止まってしまう人が多いので、前章でポイントとして挙げた立式の手順に沿って一緒に一つずつ考えていきましょう。
■立式の手順
①回転軸を確認する
②回転軸を積分変数として(上記なら \(\small t\))、始点と終点を積分範囲とする
③断面の半径を積分変数 \(\small t\)の関数 \(\small R(t)\)として表す
徹底解説①:積分範囲の特定
①の回転軸を確認については、問題文から\(\small y=x\)が回転軸になるというところまでよいですね。では、②から詳しく解説していきます。
まずは、回転軸を積分変数にします。ただ、回転軸 \(\small y=x\)にはもちろん座標軸がないので、積分変数は自分で設定してあげる必要があります。ここでは、\(\small y=x\)に沿って右上方向に\(\small t\)軸を設定してあげます(下図)。斜軸回転体の問題ではこの設定の仕方しかないのでここは覚えちゃいましょう。
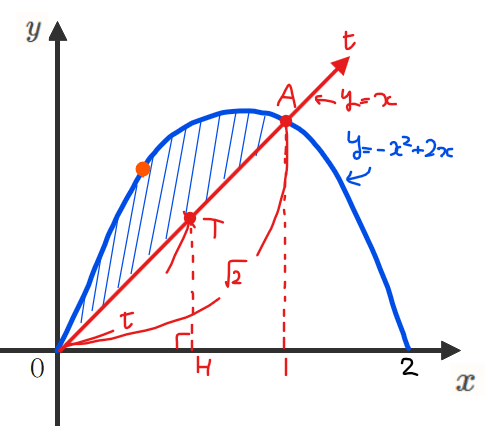
\(\small t\)軸は\(\small x\)軸が斜め45°傾いたようなイメージを持ってもらえればokです。
ここで、\(\small t\)軸上で\(\small t\)座標の値が\(\small t\)となる座標を\(\small T\)とおきます(端的に言うと、上図のように\(\small OT=t\)となる点を\(\small T\)とおく、ということ)。このように\(\small t\)軸をおくことで今回の回転体の積分範囲は、始点が原点(\(\small t=0\))、終点が点\(\small A\)(\(\small t=\sqrt{2}\))となります。
徹底解説②:回転体の半径
回転体の半径は、下図の\(\small PT\)になります。\(\small PT\)の長さは、点\(\small P\)の座標を\(\small P(s,-s^2+2s)\)(ただし\(\small 0≦ s ≦1\))とおくことで、点\(\small P\)と直線 \(\small x-y=0\)(\(\small y=x\)を式変形しただけ)に対して点の距離の公式を使うことで計算できて、

\begin{equation}
\begin{split}
PT&=\frac{|s-(-s^2+2s)|}{\sqrt{1^2+(-1)^2}}\\
&=\frac{|s^2-s|}{\sqrt{2}}\\
&=\frac{s-s^2}{\sqrt{2}}\\
\end{split}
\end{equation}
(補足)\(\small |s^2-s|\)の絶対値計算
\(\small s\)が点\(\small P\)の\(\small x\)座標であり、曲線 \(\small y=-x^2+2x\)上を点\(\small O\)から点\(\small A\)までしか動かないことから、\(\small 0≦s≦1\)となるので、\(\small s≧0\)、\(\small s-1≦0\)なので、
$$\color{red}{s^2-s=s(s-1)≦0}$$
より、絶対値の中身が負なので、\(\small |s^2-s|=\color{red}{-(s^2-s)=s-s^2}\)となります。
一旦、回転体の半径を\(\small s\)を使って表現できたのですが、ポイントでは、「断面の半径を積分変数 \(\small t\)の関数 \(\small R(t)\)として表す」とあるので、ここからは半径\(\small PT\)を回転軸の座標である\(\small t\)で表すことを考えます。
そのためには変数\(\small s\)と変数\(\small t\)を紐づける関係式が必要になります。
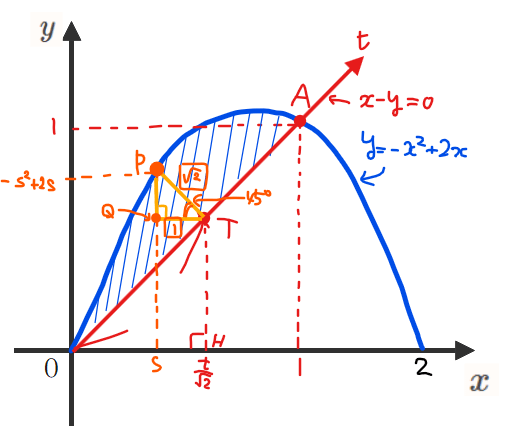
関係式は数式だけを見ていてもわからないので、実際の座標平面上で図形的に考える必要があります。すると、△\(\small PQT\)は45°の直角二等辺三角形になっているので、\(\small PT:QT=\sqrt{2}:1\)より、\(\small \displaystyle QT=\frac{1}{\sqrt{2}}PT=\frac{s-s^2}{2}\cdots①\)となります。
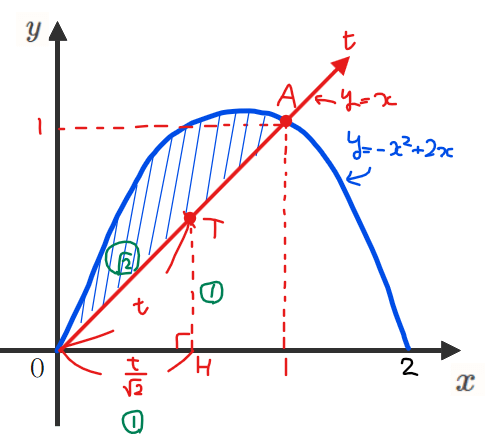
また、上図で△\(\small OTH\)が45°の直角二等辺三角形で\(\small OT=t\)であることから、\(\small \displaystyle OH=\frac{t}{\sqrt{2}}\cdots②\)です。
\(\small x\)座標の位置関係から、\(\small OH=s+QT\)なので、①,②の結果から、\(\small \displaystyle OH=\color{red}{\frac{t}{\sqrt{2}}=s+\frac{s-s^2}{2}}\)、すなわち
\begin{equation}
\begin{split}
\frac{t}{\sqrt{2}}&=s+\frac{s-s^2}{2}\\
\frac{t}{\sqrt{2}}&=\frac{3s-s^2}{2}\\
t&=\color{red}{\frac{3s-s^2}{\sqrt{2}}\cdots③}\\
\end{split}
\end{equation}
これで、所望の\(\small s\)と\(\small t\)の関係式が得られたわけですが、半径 \(\small \displaystyle PT=\frac{s-s^2}{\sqrt{2}}\)を \(\small t\)の関数にするには③の式を「\(\small s=\cdots\)」の形にして代入しないといけません。でも③は \(\small s\)の2次関数ですから、結構面倒です。
このような場合は、積分変数を回転軸\(\small t\)の積分ではなく、\(\small s\)の積分に変換することで解くことができます。
徹底解説③:積分の立式
置換積分で解いていく場合のポイントは以下の通りです。
■置換積分の使い道
置換積分は半径を回転軸の関数で表すことができないときに使うべし!
<置換積分の手順>
①回転軸を積分変数として一旦立式する
②置換積分で積分変数を変換する
└積分範囲の変換
└微小変化量の変換
では、実際に立式していきます。まずは、一旦積分変数は回転軸である\(\small t\)として立式すると、
\begin{equation}
\begin{split}
V&=\int_{0}^{\sqrt{2}}\pi (PT)^2 dt\\
&=\int_{0}^{\sqrt{2}}\pi \left( \frac{s-s^2}{\sqrt{2}}\right)^2 dt\quad \cdots (*)\\
\end{split}
\end{equation}
こんな感じです。積分範囲と積分変数が \(\small t \)になっていて、半径の関数だけが\(\small s\)の関数になっています。そして、半径の関数を\(\small t\)の関数にすると計算が鬼難しくなるので、積分範囲、積分変数の方を \(\small s\)に合わせようというのがこれからやりたいことになります。
はじめに積分範囲の変換からすると、\(\small t\)が\(\small 0~\sqrt{2}\)まで動くとき、\(\small s\)の値の範囲は、下図より\(\small 0~1\)なので、積分範囲は、\(\small 0≦s≦1\)となります。

微小変化量の変換についは、\(\small \displaystyle t=\frac{3s-s^2}{\sqrt{2}}\)の両辺の微分することで
$$dt=\frac{3-2s}{\sqrt{2}}ds$$
よって、これらの結果を\(\small (*)\)に代入することで求める体積の積分式は
\begin{equation}
\begin{split}
V&=\int_{\color{red}0}^{\color{red}1}\pi \left( \frac{s-s^2}{\sqrt{2}}\right)^2 \times \color{red}{\frac{3-2s}{\sqrt{2}}ds}\\
&=\frac{\pi}{2\sqrt{2}}\int_{0}^{1} (s-s^2)^2(3-2s)ds\\
&=\frac{\pi}{2\sqrt{2}}\int_{0}^{1}s^2(s-1)^2(3-2s)ds\\
\end{split}
\end{equation}
これで、積分の式は立式できたのであとは頑張って計算していきます。
徹底解説④:積分計算と解答
多項式の積分なので、式を展開してから積分していきます。
\begin{equation}
\begin{split}
V&=\frac{\pi}{2\sqrt{2}}\int_{0}^{1}s^2(s-1)^2(3-2s)ds\\
&=\frac{\pi}{2\sqrt{2}}\int_{0}^{1}s^2(s^2-2s+1)(3-2s)ds\\
&=\frac{\pi}{2\sqrt{2}}\int_{0}^{1}s^2(-2s^3+7s^2-8s+3)ds\\
&=\frac{\pi}{2\sqrt{2}}\int_{0}^{1}(-2s^5+7s^4-8s^3+3s^2)ds\\
&=\frac{\pi}{2\sqrt{2}}\bigg[-\frac{1}{3}s^6+\frac{7}{5}s^5-2s^4+s^3\bigg]_{0}^{1}\\
&=\frac{\pi}{2\sqrt{2}}\left(-\frac{1}{3}+\frac{7}{5}-2+1\right)\\
&=\frac{\pi}{2\sqrt{2}}\left(\frac{-5+21-15}{15}\right)\\
&=\frac{\pi}{2\sqrt{2}}\times \frac{1}{15}\\
&=\color{red}{\frac{\pi}{30\sqrt{2}}\quad \cdots (答)}\\
\end{split}
\end{equation}
(解答)
\(\small \displaystyle \color{red}{\frac{\pi}{30\sqrt{2}}}\)
【問題2】ドーナツ型の体積(円の回転体)
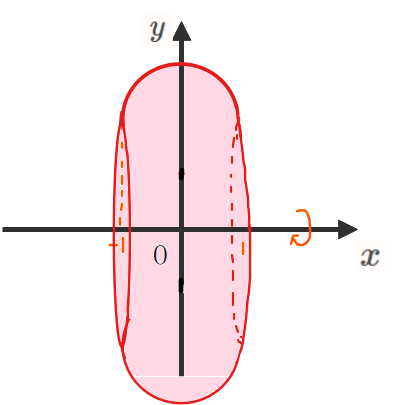
領域 \(\small x^2+(y-2)^2≦1\)を\(\small x\)軸まわりに一回転させたときにできる回転体の体積を求めよ。
皆さんもご存じの通り、この円を\(\small x\)軸を回転軸として1回転させると中央が空洞のドーナツ型になります。今回は下図のようなドーナツ型の体積の求め方を解説していきます。
不等式 \(\small x^2+(y-2)^2≦1\)で表される領域を図示すると下図赤線部分になります。
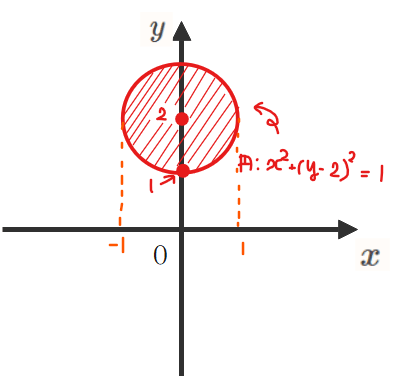
回転軸は\(\small x\)軸、\(\small x\)の積分範囲は上図より\(\small -1≦x≦1\)となります。求める体積を\(\small V\)とすると、
$$V=\int_{-1}^{1} \pi \{R(x)\}^2 dx$$
となるので、あとは回転体の半径を求めていけばよさそうです。ここで回転軸と領域(赤斜線の円内部)の位置関係をみて『バームクーヘンだ!』とピンと来た人はかなり演習が積めていると思います。ただ、ほとんどの人が「いきなり、バームクーヘン?おなかすいたなぁ…」という状態だと思うので、ポイントを再掲します。詳しくは冒頭でも紹介した「回転体の体積の求め方を徹底解説(x軸、y軸まわり、バームクーヘン型積分)」の記事を確認しましょう。
■バームクーヘン型積分を使うタイミング
回転軸と領域が離れていたら『バームクーヘン』
→全体部分から空洞部分を引き算で求めよ!
ここで言いたいのは、今回のように回転軸と回転させる領域が離れている場合は、回転させると中央に空洞ができるので、空洞部分の体積を全体から引き算する方針で体積計算していけばよい、ということです。なので、名前は知らなくても方針が理解できていればokです。
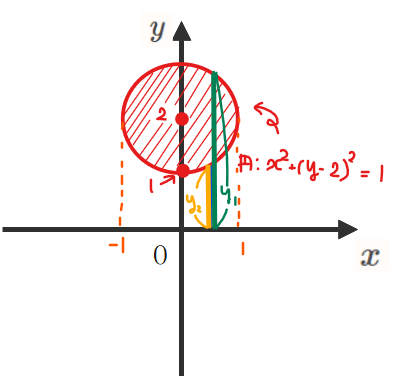
長い方の回転体の円の半径を\(\small \color{green}{y_1}\)、短い方の回転体の円の半径を\(\small \color{orange}{y_2}\)とすると、
\begin{equation}
\begin{split}
&\color{green}{y_1=2+\sqrt{1-x^2}}\quad \cdots①\\
&\color{orange}{y_2=2-\sqrt{1-x^2}}\quad \cdots②\\
\end{split}
\end{equation}
となります。
(補足)半径の計算方法について
\(\small y_1\)、\(\small y_2\)の求め方について補足します。円の方程式 \(\small x^2+(y-2)^2=1\)を\(\small y\)について解くと
\begin{equation}
\begin{split}
(y-2)^2&=1-x^2\\
y-2&=\pm \sqrt{1-x^2}\\
y&=2\pm \sqrt{1-x^2}\\
\end{split}
\end{equation}
となります。ここで、\(\small \color{red}{y=2+ \sqrt{1-x^2}}\)の方は、\(\small 0≦x≦1\)より\(\small y\)の取り得る値の範囲は、\(\small \color{red}{2≦y≦3}\)(\(\small x=0\)のとき\(\small y=3\)、\(\small x=1\)のとき、\(\small y=2\))で円の上半分を表しています。一方で、\(\small \color{red}{y=2- \sqrt{1-x^2}}\)の方は、\(\small \color{red}{1≦y≦2}\)(\(\small x=0\)のとき\(\small y=1\)、\(\small x=1\)のとき、\(\small y=2\))で、円の下半分を表しています。
\(\small y_1\)、\(\small y_2\)を使って求める体積を立式する場合、下図のような全体部分(半径\(\small y_1\)の緑円部分)から内部の空洞部分(半径\(\small y_2\)のオレンジ円部分)の体積を引き算すればよいので

$$V=\int_{-1}^{1} \pi \color{green}{(y_1)^2}dx-\int_{-1}^{1} \pi \color{orange}{(y_2)^2}dx\quad \cdots(*)$$
と立式できます。
補足:立式の考え方(別解)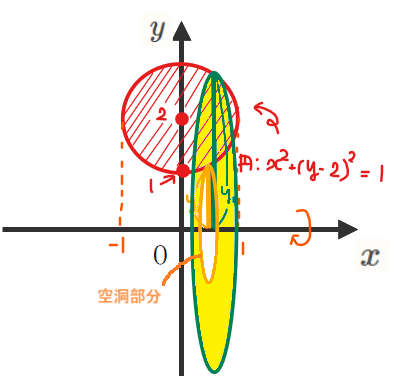
上図の断面である黄色部分を\(\small -1≦x≦1\)の範囲で積み重ねると考えると、回転体の断面積は\(\small \pi (y_1)^2-\pi (y_2)^2\)なので、
$$V=\color{red}{\int_{-1}^{1} \left( \pi (y_1)^2-\pi (y_2)^2 \right) dx}$$
なります。
どちらの考え方でも結果は同じ式になるので、考えやすい方を使えばokです。
\(\small (*)\)に①、②を代入すると
\begin{equation}
\begin{split}
V&=\int_{-1}^{1} \pi \left(2+\sqrt{1-x^2} \right)^2dx\\
&\quad -\int_{-1}^{1} \pi \left(2-\sqrt{1-x^2} \right)^2dx\\
&=\pi \int_{-1}^{1} \left(4+4\sqrt{1-x^2}+(1-x^2) \right)dx\\
&\quad -\pi \int_{-1}^{1} \left(4-4\sqrt{1-x^2}+(1-x^2) \right)dx\\
&= 8\pi \int_{-1}^{1} \sqrt{1-x^2}dx\\
&= 8\pi \times \frac{\pi}{2}\\
&=\color{red}{4\pi^2 \quad \cdots (答)}\\
\end{split}
\end{equation}
(補足)\(\small \displaystyle \int_{-1}^{1} \sqrt{1-x^2}dx\)の積分計算
この積分の形を見たら半円の面積だと気づけるようにしておくと便利です。一般的には半径\(\small r\)の半円の面積は\(\small \displaystyle \color{red}{\int_{-r}^{r} \sqrt{r^2-x^2}dx}\)となります。今回であれば\(\small r=1\)、つまり半径1の半円の面積なので、\(\small \displaystyle \color{red}{\int_{-1}^{1} \sqrt{1-x^2}dx=\frac{\pi}{2}} \)と積分計算しなくても求めることができます。もちろん実際に、積分計算して求めてもよいのですが、その場合、\(\small x=\sin \theta\)で置換積分をする必要があるので、計算も大変ですし時間もかかります。
(解答)
\(\small 4 \pi^2\)
【知っトク】ハップスギュルダンの定理
最後に、ドーナツ型の体積を求めるときに使える裏ワザを紹介します。入試の解答欄には書けませんが検算として使えるので覚えておくとよいと思います。
【公式と直観的な証明】ハップスギュルダンの定理とは?
■ハップスギュルダンの定理
断面積\(\small S\)の領域Dを回転軸 \(\small \ell\)を軸に1回転させることで作られるドーナツ型の体積\(\small V\)は、領域Dの重心と回転軸 \(\small \ell\)との距離を\(\small d\)とすれば
$$\color{red}{V=2 \pi d S}$$
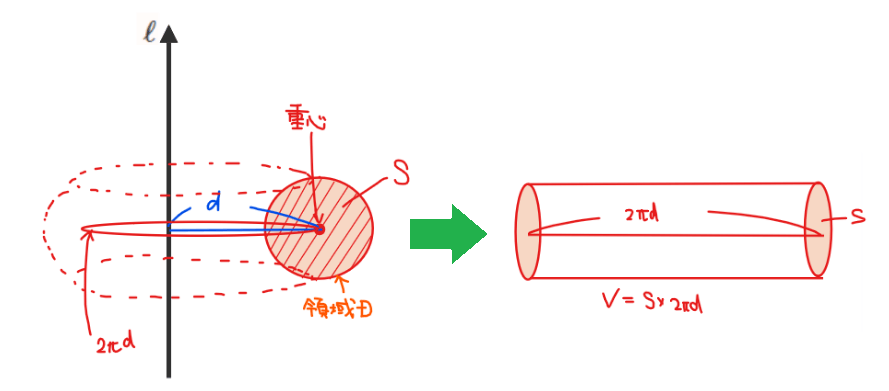
公式の直感的なイメージとしては、左上図のように、ドーナツ型の立体を断面で切って一直線に伸ばすと右上図のような円柱状の立体になり、この体積は底面積が\(\small S\)、高さが\(\small 2 \pi d\)の円柱になるので、求める立体の体積は\(\small V=2 \pi d S\)になるというのがハップスギュルダンの定理です。
【問題2の別解】ハップスギュルダンの定理を用いた解法
ここでは、問題2をハップスギュルダンの定理を使って解いてみます。とても簡単に計算できるので、検算をするときに非常に便利です。
領域 \(\small x^2+(y-2)^2≦1\)は半径1の円なので、断面積は \(\small \pi\)、回転軸と円の重心との距離は、\(\small x\)軸と円の中心 \(\small (0,2)\)との距離なので、2になります。
よって、ハップスギュルダンの定理から
\begin{equation}
\begin{split}
V=2\pi d S &=2 \pi \times \color{blue}2 \times \color{red}\pi\\
&=4 \pi^2 \quad \cdots (答)\\
\end{split}
\end{equation}
このように簡単に計算できました。
本記事のまとめ
今回は、斜軸回転体の体積とドーナツ型の立体の体積の求め方について解説しました。いずれの体積計算の場合であっても、立式の手順は変わらずで、問題によって半径の関数を積分変数で表せない場合があったり、全体から空洞部分を引き算してあげる必要があったりというアレンジが加わっている感じでしたね。
■立式の手順
①回転軸を確認する
②回転軸を積分変数として(上記なら \(\small t\))、始点と終点を積分範囲とする
③断面の半径を積分変数 \(\small t\)の関数 \(\small R(t)\)として表す
■置換積分の使い道
置換積分は半径を回転軸の関数で表すことができないときに使うべし!
<置換積分の手順>
①回転軸を積分変数として一旦立式する
②置換積分で積分変数を変換する
└積分範囲の変換
└微小変化量の変換
■バームクーヘン型積分を使うタイミング
回転軸と領域が離れていたら『バームクーヘン』
→全体部分から空洞部分を引き算で求めよ!
あとは、ドーナツ型の体積を簡単に求める裏ワザとして、ハップスギュルダンの定理を紹介しました。余裕がある人は覚えておくと検算の時に便利です。
■ハップスギュルダンの定理
断面積\(\small S\)の領域Dを回転軸 \(\small \ell\)を軸に1回転させることで作られるドーナツ型の体積\(\small V\)は、領域Dの重心と回転軸 \(\small \ell\)との距離を\(\small d\)とすれば
$$\color{red}{V=2 \pi d S}$$
今回はここまでです。お疲れさまでした!







コメント