軸・定義域に文字を含んだ2次関数の最大値・最小値の場合分けのコツを徹底解説

今回は、文字を含んだ2次関数の最大値や最小値を求める問題について、パターンごとにわかりやすく解説していきます。軸や定義域に文字が含まれると最大値や最小値をどう求めればよいかわからないという人は、ぜひこの記事を最後まで読んでもらって、苦手を克服しちゃいましょう！

　本記事はこんな人におすすめ

今回の記事は次のような質問をよく見かけるため、本記事で1からしっかり解説しようと決意しました。

2次関数の問題で、定義域に定数aを含む最大最小の問題がわからない…
参考書の解説を読んでも解き方がよくわからない…
文字を含んだ2次関数の場合分けの方法がよくわからない…

こんな悩みを抱えている人向けに、この記事では問題のパターンごとに場合分けの方法や考え方のコツを教えます。

　本記事のレベル

重要度

低

1

2

3

4

5

高
難易度

易しい

1

2

3

4

5

難しい
暗記/理解

暗記重視

1

2

3

4

5

理解重視

【はじめに】文字が含まれると難しくなる理由
文字を含んだ最大値・最小値の求め方
まとめ

【はじめに】文字が含まれると難しくなる理由

文字が出てこなければ2次関数の問題は余裕で解けるのに、文字が出てきた途端考える気力が遠のく…。こう思っている高校生はたくさんいます。では、なぜ多くに人は文字が含まれると難しいと感じてしまうのでしょうか？

理由は、文字が含まれると具体的にグラフを描いたりイメージができなくなるからです。

■文字が含まれると難しくなる理由
具体的な値が分からない
↓
いろいろなパターンが生まれる
↓
場合分けが必要

■具体的な2次関数、定義域がある場合
　→最大値、最小値はグラフを描いて計算すれば求まる！

最小値は頂点である-6、最大値は定義域-1≦x≦5では
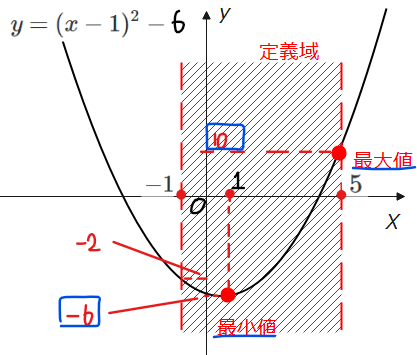
yの値が最も大きいx=5の時の値、10となる。

■文字を含んだ2次関数の場合…
　→グラフと定義域の位置関係が決まらずパターンごとに考える必要あり…

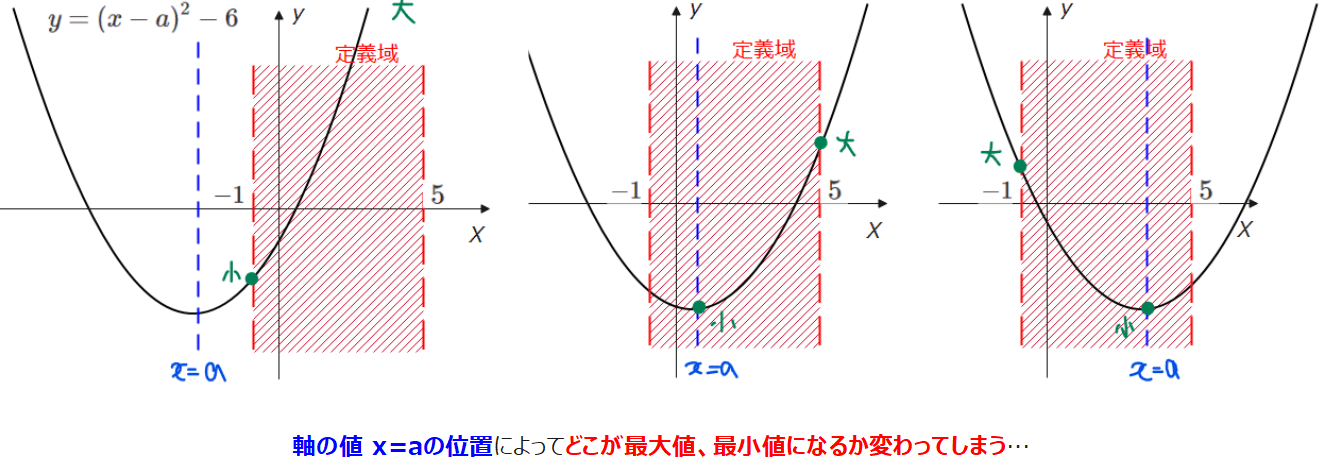
つまり、場合分けは避けて通れないわけですが、今回は場合分けが苦手な人向けに、文字を含んだ2次関数の最大値最小値の求め方を徹底解説しますのでぜひ最後まで読んで疑問を解消させましょう！

文字を含んだ最大値・最小値の求め方

2次関数の分野において文字が含まれる問題は大きく次の2種類に分けることができます。

2次関数に文字を含むパターン
定義域に文字を含むパターン

①2次関数に文字を含むパターン

問題1：文字を含む2次関数の最小値の求め方

問題(2次関数の最小値)

$\small a$を定数とする。関数$\small y=2x^2+4ax \space (-1≦x≦1) $の最小値を求めよ。

■2次関数に文字を含むときの最小値を求めるコツ
　軸の位置が定義域の左外、内側、右外の3パターンで場合分け！

　解説

軸の位置で場合分けするために、まずは軸を求めます。
$\small y=2x^2+4ax $を平方完成すると、
$$
\begin{equation}
\begin{split}
&y=2x^2+4ax \\
&y=2(x^2+2ax)\\
&y=2\{(x+a)^2-a^2\}\\
&y=2(x+a)^2-2a^2\\
\end{split}
\end{equation}
$$

よって、軸が$\small x=-a$で頂点が$\small (-a,-2a^2)$であることが分かりました。

次に、グラフを描くにあたって、軸$\small x=-a$が定義域の左側、内側、右側の3パターンに場合分けして考えます。軸の位置で場合分けする理由は、定義域内に頂点があるかないかで最小値が異なるからです。

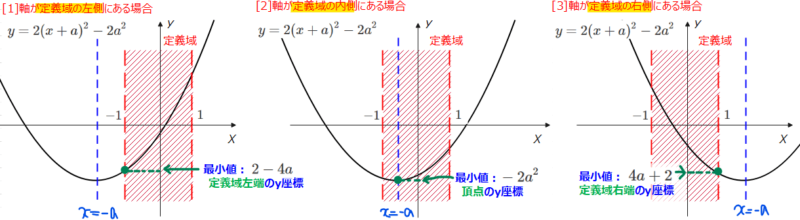
定義域$\small -1≦x≦1$の範囲（赤線部分）で$\small y$座標が最も小さくなる値が最小値になります。上の図を見るとわかりますが、そのパターンは、軸の位置によって異なっています。場合分けが苦手という人は、まずはこの感覚をしっかり理解しましょう。

[1]軸が定義域の左側にある場合
図を描くと以下の通りです。青点線が軸$\small x=-a$、赤線部分が定義域$\small -1≦x≦1$です。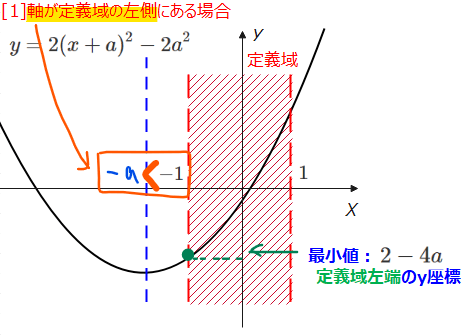

この場合は、図を見れば一目瞭然ですが必ず$\small x=-1$で$\small y$の値が最小値となります。
「軸が定義域の左側」という状況を数式で表すと、軸$\small x=-a$が定義域の左端である$\small x=-1$よりも左側にあればいいので、$\small -a<-1$が成り立ちます。左側なので不等号に「＝(イコール)」は含めないようにします。これを解くと、$\small a>1$の場合となります。
あとは最小値の計算ですが、$\small x=-1$を$\small y=2x^2+4ax $に代入すればいいので$\small \color{red}{2-4a}$と求まります。

[2]軸が定義域の内側にある場合
この場合は、軸が定義域内(赤線)にあるので必ず$\small x=-a$で$\small y$の値が最小値となります。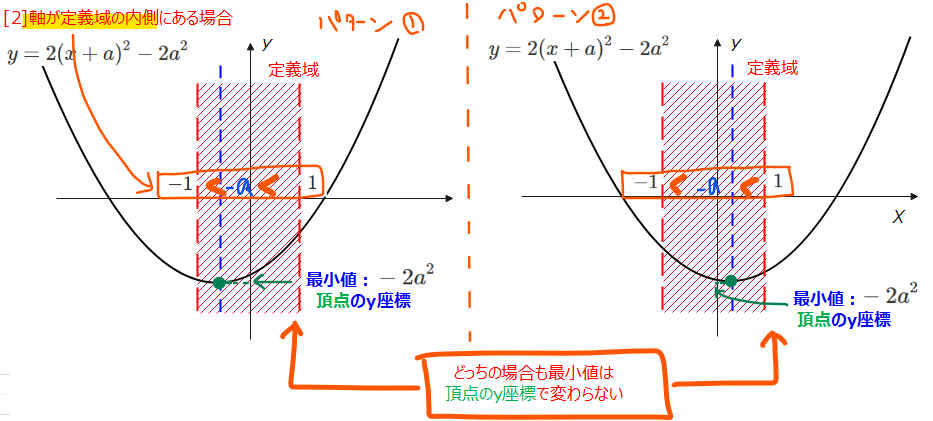

よく「定義域内でも場合分けする必要ありますか？」という質問をもらいますが、簡単なグラフを何パターンか描いてみれば場合分けが必要かどうか分かります。上記では定義域内に軸があるパターンを2つ書いてみましたが最小値はどちらも頂点の$\small y$座標なので場合分けは不要になります。
今回も「軸が定義域の内側」という状況を数式で表すと、軸$\small x=-a$が定義域$\small -1～1$の間にあればいいので、$\small -1≦-a≦1$となります。これを解くと、$\small -1≦a≦1$の場合となります。
最後に最小値は、頂点の$\small y$座標なので$\small \color{red}{-2a^2}$となります。

[3]軸が定義域の右側になる場合
この場合は、必ず$\small x=1$で$\small y$の値が最小値となります。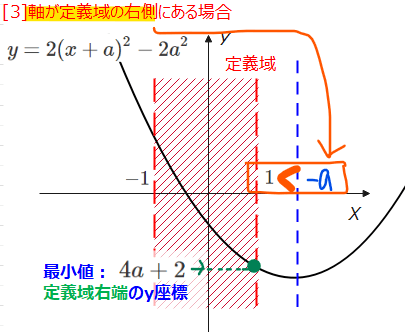

「軸が定義域の右側」という状況を数式で表すと、軸$\small x=-a$が定義域の右端である$\small x=1$よりも右側にあればいいので、$\small 1<-a$が成り立ちます。これを解くと、$\small a<-1$の場合です。
最小値は、$\small x=1$の時なので、$\small \color{red}{4a+2}$です。

よって[1]～[3]の答えを整理したものが解答です。

（解答）
$\small a>1$のとき、$\small x=-1$で最小値$\small 2-4a$、
$\small -1≦a≦1$のとき、$\small x=-a$で最小値$\small -2a^2$、
$\small a<-1$のとき、$\small x=1$で最小値最小値$\small 4a+2$をとる。

問題2：文字を含む2次関数の最大値の求め方

問題(2次関数の最大値)

$\small a$を定数とする。関数$\small y=2x^2+4ax \space (-1≦x≦1) $の最大値を求めよ。

■2次関数に文字を含むときの最大値を求めるコツ
　軸の位置が定義域の中心より左側、定義域の中心、定義域の中心より右側の3パターンで場合分け！

最大値を求めるときも軸の位置で場合分けというのは変わりません。ただ、最大値の場合は、場合分けの方法が異なります。定義域の中心を基準に左側、中心、右側の3パターンで分けていきます。

ここでよく、「2次関数の問題って、3パターンで場合分けする以外にも5パターンで場合分けする問題もあるけど何が違うの？」という質問をする人がいます。結論、5パターンで場合分けするのは、「最大値と最小値の両方を求めるとき」です。最大値と最小値を両方答えるときには、最小値の場合分け方法と最大値の場合分け方法が異なるので、組み合わせとして5パターン必要になります。

こう聞くと、「5パターンで場合分けしたり3パターンだったり混乱しちゃう…」という人もいると思いますが、効率を求めないのであれば、どんな問題も5パターンの場合分けをすれば確実に解くことができます。

■2次関数に文字を含むときの最大値、最小値を求めるコツ
軸の位置が、定義域の左外、定義域の内側(左)、定義域の内側(中央)、定義域の内側(右)、定義域の右外の5パターンで場合分けすればok。

今回は、あえて5パターンの場合分けをする方法で最大値を求めてみようと思います。そして計算の結果、結局ポイントに記載の3パターンの場合分けでよいことを確認してみましょう。

　解説

[1]軸が定義域の左外にある場合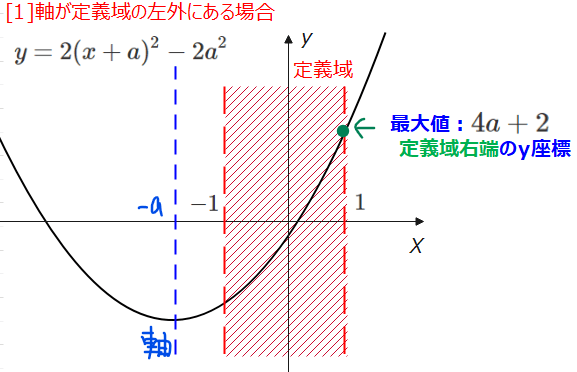

軸が定義域の左外ということは、軸が$\small x=-1$よりも左側ということなので、$\small -a<-1$すなわち、$\small a>1$の場合になります。
この時、最大値は図を描くことで、$\small x=1$の時に最大値$\small 4a+2$と分かります。

[2]軸が定義域の内側(左)にある場合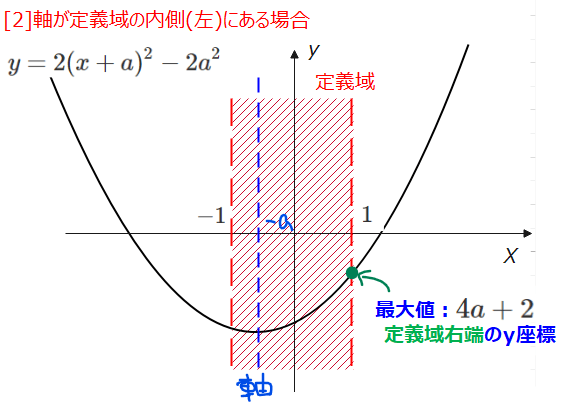

軸が定義域の内側の左半分にあるときというのは軸がどんな位置にあるときかというと、定義域の中心が$\small x=0$なので、$\small -1≦-a<0$、すなわち$\small 0<a≦1$の時になります。
このとき、最大値は図から$\small x=1$の時に最大値$\small 4a+2$と分かります。

[3]軸が定義域の内側(中央)にある場合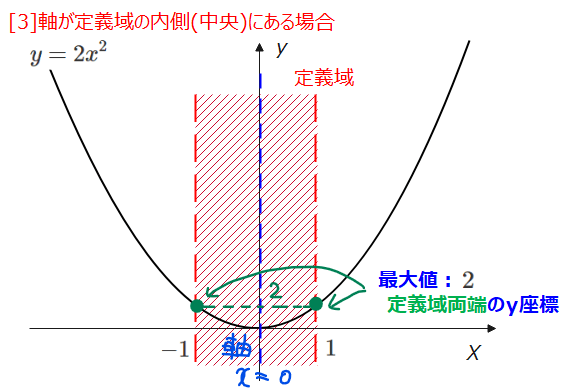

軸$\small x=-a$が定義域の中央にある場合は、具体的に$\small a$の値を求めることができます。つまり、軸が$\small x=0$になるわけなので、$\small a=0$の場合です。
すると、定数だった文字$\small a$が消えてしまうので具体的なグラフが描けて、考える2次関数は$\small y=2x^2$になります。
ところで、軸が中央にある場合をピンポイントで場合分けする理由はなぜでしょう？これは軸が中央の場合だけ最大値が定義域の両端になるからです。つまり、図を見るとわかるように、$\small x=-1$と$\small x=1$のときに最大値$\small 2$をとります。

[4]軸が定義域の内側(右)にある場合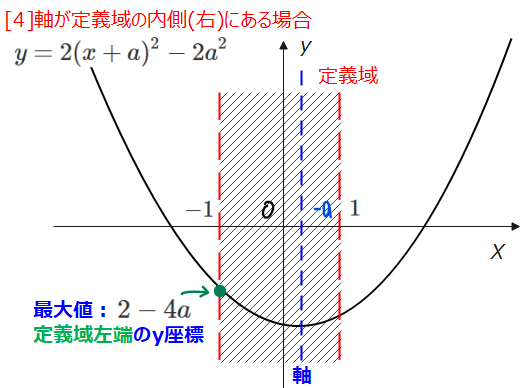

軸が定義域の内側の右半分にあるときは、軸が$\small 0<-a≦1$の範囲にあるときなので、$\small -1≦a<0$の場合になります。
このときは、図から$\small x=-1$のときに最大値$\small 2-4a$となります。

[5]軸が定義域の右外にある場合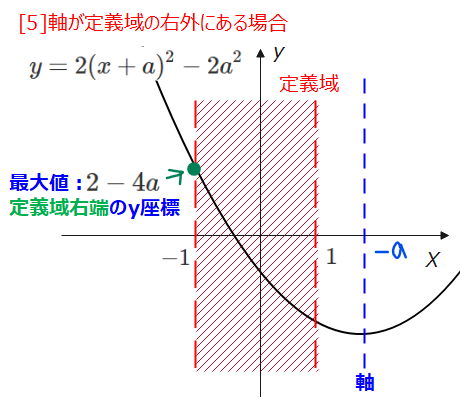

軸が定義域の右外にある場合は、$\small 1<-a$、すなわち$\small a<-1$の場合です。
このとき、最大値は図から$\small x=-1$のとき最大値$\small 2-4a$となります。

[1]～[5]の結果を整理すると、
$\small a<-1$のとき、$\small x=-1$で最大値$\small 2-4a$…[5]、
$\small -1≦a<0$のとき、$\small x=-1$で最大値$\small 2-4a$…[4]、
$\small a=0$のとき、$\small x=-1$と$\small x=1$で最大値$\small 2$…[3]、
$\small 0<a≦1$のとき、$\small x=1$で最大値$\small 4a+2$…[2]、
$\small 1<a$のとき、$\small x=1$で最大値$\small 4a+2$…[1]
となりますが、最大値のパターンは結局、緑線、黄色線、赤線の3パターンに分かれるので$\small a$の範囲を以下の通りまとめることができます。

(解答)
$\small a<0$のとき、$\small x=-1$で最大値$\small 2-4a$、
$\small a=0$のとき、$\small x=-1$と$\small x=1$で最大値$\small 2$、
$\small 0<a$のとき、$\small x=1$で最大値$\small 4a+2$.

上記の解答は、軸である$\small x=-a$が定義域の中央値である0を基準に、左側、中央、右側の3パターンに分けることで最大値を求めることができることを示しています。

このように、5パターンに分けても結局重複するパターンをまとめることで冒頭のポイントで紹介した3パターンの場合分けをすれば効率よく求めることができるわけです。

②定義域に文字を含むパターン

問題3：定義域に文字を含む場合の最小値の求め方

問題(2次関数の定義域に文字を含む場合の最小値)

$\small a$を正の定数とする。関数$\small y=2x^2-2x \space (a≦x≦a+2) $の最小値とそのときの$\small x$の値を求めよ。

■定義域に文字を含むときの最小値を求めるコツ
軸と定義域の位置関係で場合分け！
つまり、文字を含む2次関数の最小値と同様、軸の位置が定義域の左外、内側、右外の3パターンを意識した場合分けでok。

2次関数に文字が含まれるパターンでは軸に文字が含まれていたので軸の位置で場合分けしました。定義域に文字が含まれる場合でも基本的に同じ考え方で解くことができます。理由は、最大値、最小値を求めるには、軸と定義域の位置関係だけが重要だからです。どういうことかというと、軸が動こうが、定義域が動こうが、結局は軸と定義域がどんな位置関係にあるのかというパターンで最大値、最小値をとる場所が確定するので、場合分けの方針は変わらないということです。

ただし注意点としては、定義域に文字が含まれる場合は、必ずしも3パターンとは限りません。問題の条件によって、1パターンや2パターンとなる可能性もありますが、maxでも3パターンという意味なので注意しましょう。

では、細かい部分は実際の問題を通して確認していきましょう！

　解説

2次関数を平方完成すると
$$
\begin{equation}
\begin{split}
&y=2x^2-2x\\
&y=2(x^2-x)\\
&y=2\left\{\left(x-\frac{1}{2}\right)^2-\frac{1}{4}\right\}\\
&y=2\left(x-\frac{1}{2}\right)^2-\frac{1}{2}\\
\end{split}
\end{equation}
$$

このように、今回はグラフの位置は決まっていて動くのは定義域になるので定義域の位置で場合分けします。

[1]軸が定義域の左外にある場合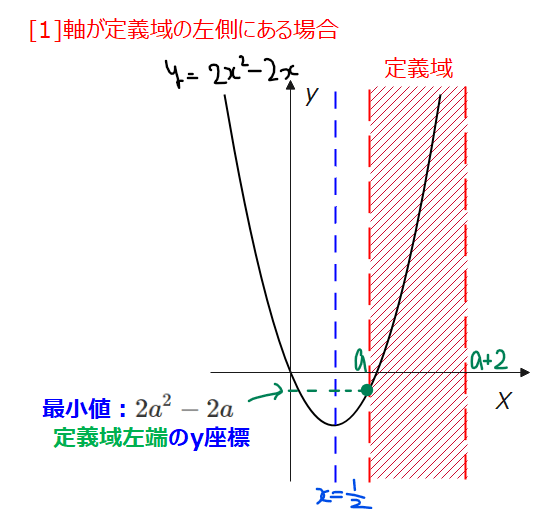

軸が定義域の左外にある場合は、定義域の左端$\small x=a$が関数$\small y=2x^2-2x$の軸である$\small x=\frac{1}{2}$よりも右側にあるときということなので、条件としては$\small \frac{1}{2}<a$のときとなります。
このとき、最小値は$\small x=a$のときの$\small y$の値になるので、$\small 2a^2-2a$です。

[2]軸が定義域内にある場合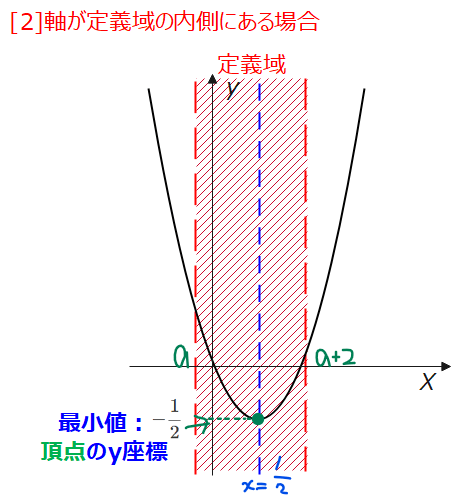

軸が定義域内にあるとき、定義域と軸の位置関係から
$$a≦\frac{1}{2}≦a+2 \quad \cdots ①$$
が成り立つ。これを解くと
$$-\frac{3}{2}≦a≦\frac{1}{2}$$
の場合ということが分かります。①の不等式が両端に文字があって解き方が怪しい人もいるかもしれないので補足すると、左半分と右半分で不等式を解いて、最後に合体させればokです。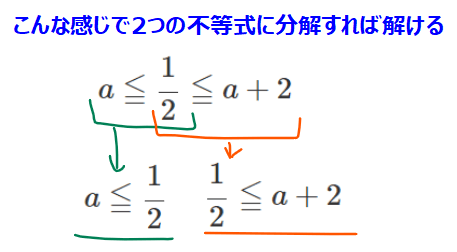

この時最小値は、グラフから常に頂点の$\small y$座標になるので、$\small x=\frac{1}{2}$のとき最小値$\small -\frac{1}{2}$です。

[3]軸が定義域の右外にある場合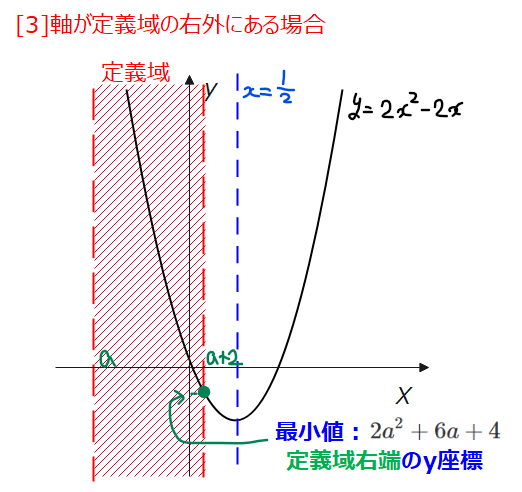

軸が定義域の右端よりも右側にあるということは、$\small a+2 < \frac{1}{2}$なので、$\small a<-\frac{3}{2}$の場合になります。
このとき、$\small x=a+2$で最小値$\small 2a^2+6a+4$となります。

最後に、[1]～[3]の結果をまとめれば答えになります。

(解答)
$\small a<-\dfrac{3}{2}$のとき、$\small x=a+2$で最小値$\small 2a^2+6a+4$、
$\small -\dfrac{3}{2}≦a≦\dfrac{1}{2}$のとき、$\small x=\dfrac{1}{2}$で最小値$\small -\dfrac{1}{2}$、
$\small \dfrac{1}{2}<a$のとき、$\small x=a$で最小値$\small 2a^2-2a$.

問題4：定義域に文字を含む場合の最大値の求め方

問題(2次関数の定義域に文字を含む場合の最大値)

$\small a$を正の定数とする。関数$\small y=2x^2-2x \space (a≦x≦a+2) $の最大値とそのときの$\small x$の値を求めよ。

■定義域に文字を含むときの最大値を求めるコツ
最小値と同様、軸と定義域の位置関係で場合分け！
つまり、軸の位置が定義域の中心より左側、定義域の中心、定義域の中心より右側の3パターンを意識した場合分けでok。

　解説

定義域、$\small a≦x≦a+2$の中心の$\small x$座標は、$\small \frac{a+(a+2)}{2}=\frac{2a+2}{2}=a+1$なので、定義域の中心、$\small x=a+1$を基準に場合分けしていきます。

[1]軸が定義域の中心$\small x=a+1$よりも左側にある場合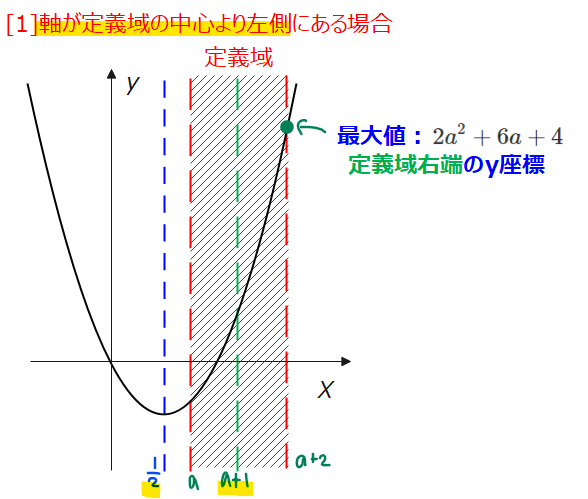

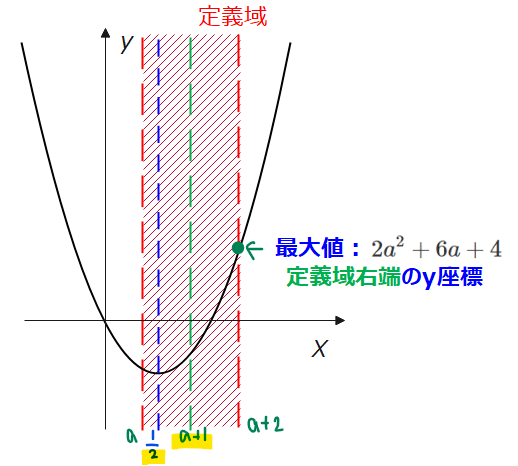
上図の緑点線が定義域の中心$\small x=a+1$、青点線が軸$\small x=\frac{1}{2}$、赤線部分が定義域$\small a≦x≦a+2$です。
軸が定義域の中心よりも左側なので、$\small \frac{1}{2}<a+1$の不等式が成り立ちます。
これを解くと、
$$
\begin{equation}
\begin{split}
&a+1>\frac{1}{2}\\
&2a+2>1\\
&2a>-1\\
&a>-\frac{1}{2}\\
\end{split}
\end{equation}
$$
よって、今回考える$\small a$の範囲は、$\small a>-\dfrac{1}{2}$になります。
このとき、図からもわかるように軸が定義域の中にあっても、外にあっても最大値は定義域の右端になるので、$\small x=a+2$のとき最大値$\small 2a^2+6a+4$となります。

[2]軸が定義域の中心$\small x=a+1$にある場合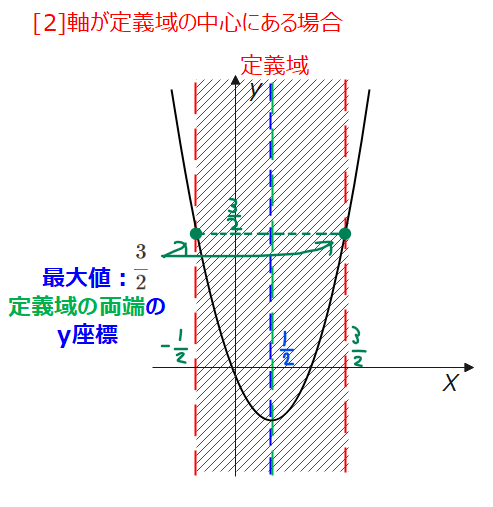

定義域の中心=軸であることから、$\small a+1=\frac{1}{2}$となるので、これを解くと$\small a=-\frac{1}{2}$が今回考える場合です。
$\small a$の値が求まったので、定義域は$\small -\frac{1}{2}≦x≦\frac{3}{2}$とわかるのでグラフを描くことができます。図から、定義域の両端で最大値をとるパターンになるので、$\small x=-\dfrac{1}{2}、\dfrac{3}{2}$で最大値$\small \dfrac{3}{2}$をとることが分かります。

[3]軸が定義域の中心$\small x=a+1$よりも右側にある場合

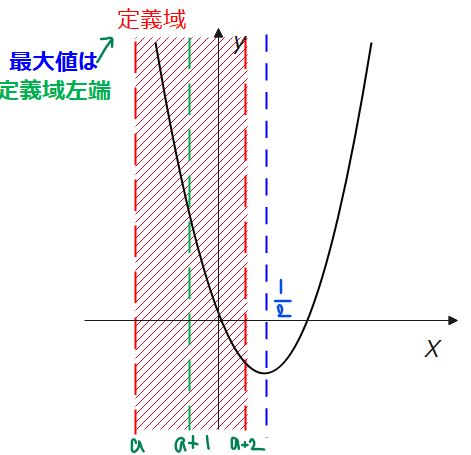
定義域の中心と軸の位置関係から、
$$
\begin{equation}
\begin{split}
&a+1<\frac{1}{2}\\
&2a+2<1\\
&2a<-1\\
&a<-\frac{1}{2}\\
\end{split}
\end{equation}
$$
よって、$\small a<-\dfrac{1}{2}$が今回考える場合です。
このとき、最大値は定義域の左端、$\small x=a$のときなので、$\small 2a^2-2a$になります。

(解答)
$\small a<-\dfrac{1}{2}$のとき、$\small x=a$で、最大値$\small 2a^2-2a$、
$\small a=-\dfrac{1}{2}$のとき、$\small x=-\dfrac{1}{2}、\dfrac{3}{2}$で最大値$\small \dfrac{3}{2}$、
$\small a>-\dfrac{1}{2}$のとき、$\small x=a+2$で最大値$\small 2a^2+6a+4$.