本記事では、「確率問題を解く上で大事になる余事象の考え方」を「良問を通して解説」していきます。
- 余事象について知りたい!
- 余事象の問題の解き方のコツを知りたい!
- 受験対策として、応用的な問題を解きたい!
【解説編】余事象の復習
1.1 余事象とは
余事象の説明をする前に、1つだけ用語の説明です。
事象とは?
とある出来事(パターン)のこと。
では本題の余事象についての解説です。
余事象とは?
とある出来事以外の出来事のこと。
どうでしょう?「余」事象という言葉は、読んで字のごとく、「余った事象(出来事)」という意味なのですが、この説明だけだとなんだか漠然としていてイメージわかないですよね?
大丈夫です。具体的なイメージで理解していきましょう!
1.2 余事象の具体例
例えば皆さんが洋服の買い物をしているとします。気に入った服が、A、B、Cの3着あるのですが、お小遣い的に1着しか買えません。どれか1着は必ず買うとき、「Aの服を買う」、「Bの服を買う」、「Cの服を買う」というのが「事象」です。そして、「Aの服を買う」という事象の余事象は「それが起こらない事象(出来事・パターン)」なので「BかCの服を買う」となります。
このように、とある出来事以外の出来事のことを「余事象」といいます。
1.3 余事象の使い道
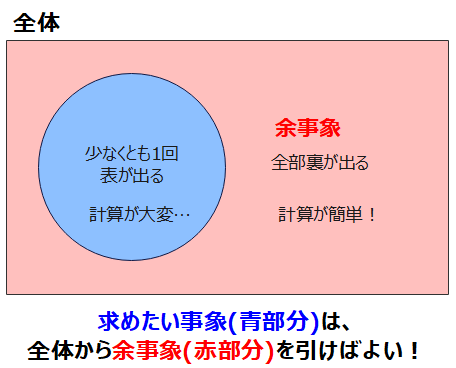
数学の問題で確率を求めるときに、余事象を使うと簡単に解ける問題があります。それは、求めるパターンが非常に多いときです。具体的には、「少なくとも…」や「~以上/未満」などが問題文中に含まれることが多いです。
たとえば、「コインを10回投げたときに、少なくとも表が1回出る確率」は、そのまま考えようとすると、「表が1回出る場合、2回出る場合、…、10回出る場合」とかなり多くのパターンを考える必要がありますが、余事象に着目すると、「表が1回も出ない場合(つまり全部裏)」の1パターンのみを考えて、全体から引き算してあげればよいので、とても簡単に計算できます。
【演習編】余事象の問題2選
ここからは実際の問題を通して余事象について解説します。
問題1(さいころの最大値と最小値)
複雑な余事象はしっかりベン図を描いて考えることが重要!
ベン図が描けたら、あとはベン図に従って集合計算を用いて確率を求めればok。
さいころを振って出た目の最大値と最小値の差が5になるということは、最大値が6で最小値が1であることが確定するので、この問題は、「さいころを\(\small n\)回振ったときに、1と6の目が少なくても1回は出る確率」を求める問題と言い換えることができます。なので、余事象を考えることにしましょう。
複雑な余事象はベン図を描いた方がよい
この問題の余事象はどうなるでしょうか?「さいころを\(\small n\)回振って1も6も1回も出ない確率」でしょうか?
このように考えてしまった人は要注意!実はこれは違います。理由は、逆に「1も6も出ない場合」の余事象が問題で求めたい事象と合致するかを考えたときに、これだと「1は出るけど6は出ない」などのパターンが含まれてしまいます。今回は1も6もどちらも1回は出てほしいので、余事象としては不適切です。
今回のように事象自体が複雑な場合は、感覚的に言語化するのではなく、しっかりとベン図を描いて整理することが大事です。
求めたい確率をベン図で可視化
先程の「さいころを\(\small n\)回振ったときに、1と6の目が少なくても1回は出る」をもう少し分解すると「さいころを\(\small n\)回振ったときに、少なくても1の目が1回は出る」かつ「さいころを\(\small n\)回振ったときに、少なくても6の目が1回は出る」です。2つの事象のAND条件になっていたわけです。
これをベン図で描くとこうなります。
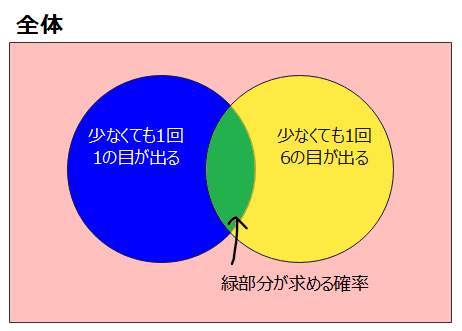
今回求めるのは緑色の部分なので、あとは集合の知識を駆使して計算していきましょう。
ちなみに、先程間違い例として紹介した「さいころを\(\small n\)回振って1も6も1回も出ない」事象は、上のベン図でいうと赤色の部分になっているので、緑の余事象としては不適切というのが図で見ると一目瞭然です。(ベン図を積極的に活用しましょう!)
集合知識を活用した確率計算
ベン図の緑の確率を求める計算をしていきましょう。緑が起きる確率を\(\small \mathrm{P}(緑)\)、同様に青、黄色が起きる確率をそれぞれ\(\small \mathrm{P}(青)\)、\(\small \mathrm{P}(黄)\)とすると、
$$
\begin{equation}
\begin{split}
\mathrm{P}(緑)&=\mathrm{P}(青\cap黄) \cdots①\\
\end{split}
\end{equation}
$$
≪重要≫集合計算の基礎(共通集合と和集合)
$$
\begin{equation}
\begin{split}
&\mathrm{P}(青\cup黄)=\mathrm{P}(青)+\mathrm{P}(黄)- \mathrm{P}(青\cap黄)\\
&\mathrm{P}(青\cap黄)=\mathrm{P}(青)+\mathrm{P}(黄)- \mathrm{P}(青\cup黄)\cdots②\\
\end{split}
\end{equation}
$$
①、②から
$$\mathrm{P}(緑)=\mathrm{P}(青)+\mathrm{P}(黄)- \mathrm{P}(青\cup黄)\cdots③$$
あとはぞれぞれの確率を求めればよく、青色事象の確率であれば、余事象を活用して「1の目が1度も出ない確率を全体から引き算」で求めればよく、\(\small \mathrm{P}(青)=1-\left(\frac{5}{6}\right)^n\)。
黄色事象の確率も同様にして、\(\small \mathrm{P}(黄)=1-\left(\frac{5}{6}\right)^n\)。
最後に\(\small \mathrm{P}(青\cup黄)\)は言語化すると「青と黄の和集合の確率」すなわち「少なくても1または6が1回は出る確率」となるので、余事象である「1も6も1度も出ない確率」を求めればよく、\(\small \mathrm{P}(青\cup黄)=1-\left(\frac{4}{6}\right)^n\)。
以上を③に代入すると
$$
\begin{equation}
\begin{split}
\mathrm{P}(緑)&=\left( 1-\left(\frac{5}{6}\right)^n \right)+\left( 1-\left(\frac{5}{6}\right)^n \right)- \left(1-\left(\frac{4}{6}\right)^n\right)\\
&=1-2 \cdot \left(\frac{5}{6}\right)^n+\left(\frac{4}{6}\right)^n\\
&=\frac{6^n-2\cdot 5^n + 4^n}{6^n}
\end{split}
\end{equation}
$$
(解答)
$$ \frac{6^n-2\cdot 5^n + 4^n}{6^n}$$
問題2(さいころの積)
こちらも集合の知識を活用した確率計算としては王道の問題かなと思いますが、少し複雑になっています。
ベン図で可視化
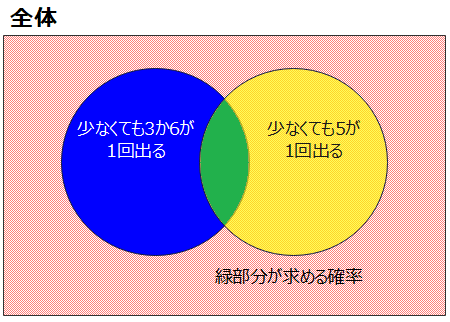
さいころの目の積が15で割り切れるということは、3の倍数と5の倍数の両方が少なくとも1つ入っている必要があります。具体的には、3の倍数は「3か6」、5の倍数は「5」なので、問題を言い換えると「1個のさいころを\(\small n\)回投げた目の積に、「少なくても3か6が1回」かつ「少なくとも5が1回」出る確率」となります。
ベン図も以下の通りで緑部分が求めたい確率です。
細かい条件について
ちょっと細かいですが先に問題の前提について述べておきましょう。これまでの考察から明らかですが15で割り切れるためにはさいころは最低2回振る必要があるので、以下\(\small n≧2\)とします。
事象Aの確率計算
少なくても3か6が1回出る事象をAとして、その確率を\(\small \mathrm{P(A)}\)とすると、余事象「3も6も出ない確率」を考えることで、
$$\mathrm{P(A)}=1-\left(\frac{4}{6}\right)^n\cdots①$$
事象Bの確率計算
次に、少なくとも5が1回出る事象をBとして、その確率を\(\small \mathrm{P(B)}\)とすると、余事象「5が1度も出ない確率」を考えることで、
$$\mathrm{P(B)}=1-\left(\frac{5}{6}\right)^n\cdots②$$
全体の確率計算
求める確率は、\(\small \mathrm{P(A\cap B)}\)なので、
$$
\begin{equation}
\begin{split}
&\mathrm{P(A\cup B)}=\mathrm{P(A)}+\mathrm{P(B)}- \mathrm{P(A\cap B)}\\
&\mathrm{P(A\cap B)}=\mathrm{P(A)}+\mathrm{P(B)}- \mathrm{P(A\cup B)}\cdots③\\
\end{split}
\end{equation}
$$
最後に、\(\small \mathrm{P(A\cup B)}\)を求める必要があります。これは「少なくても3か6が1回出る事象」と「少なくとも5が1回出る事象」の和集合なので、「少なくとも3か6か5が1回出る事象」となり、その確率は
$$\mathrm{P(A\cup B)}=1-\left(\frac{3}{6}\right)^n\cdots④$$
①、②、④を③に代入すると
$$
\begin{equation}
\begin{split}
\mathrm{P(A\cap B)}&=\mathrm{P(A)}+\mathrm{P(B)}- \mathrm{P(A\cup B)}\\
&=\left(1-\left(\frac{4}{6}\right)^n \right)+\left( 1-\left(\frac{5}{6}\right)^n \right)\\
&\quad-\left( 1-\left(\frac{3}{6}\right)^n \right)\\
&=1-\left(\frac{4}{6}\right)^n -\left(\frac{5}{6}\right)^n+\left(\frac{3}{6}\right)^n \\
&=\frac{6^n-4^n-5^n+3^n}{6^n}
\end{split}
\end{equation}
$$
最後の仕上げ
途中で\(\small n≧2\)として計算を進めていましたが、求めた答えに\(\small n=1\)を入れると0となり、さいころを1回振っただけでは15で割れることはあり得ないという事実とも合致しているので、\(\small n=1\)としても不都合が生じません。よって、題意の通り自然数\(\small n\)に対して答えは成立することが分かりました。
(解答)
$$\frac{6^n-4^n-5^n+3^n}{6^n}$$
気を付けられたい失敗例の紹介
■気を付けられたい失敗例
以下Aさんの考え方について、皆さんもどこに間違いがあるか探してみましょう。
~Aさんの考え方(間違いあり)~
「3の倍数と5の倍数の両方が少なくとも1つ入る確率」だから、パターンとしては以下のベン図で、オレンジ枠(3と5が1回は出る)、紫枠(6と5が1回は出る)、緑色(3,5,6が1回は出る)の3つの合計部分を求めれば答えになりそう。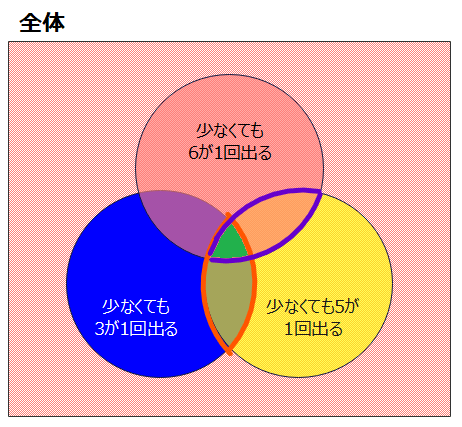
それぞれ、オレンジ、紫枠部分は\(\small 1-\left(\frac{4}{6}\right)^n\)、緑部分は\(\small 1-\left(\frac{3}{6}\right)^n\)だから、求める確率は、オレンジ+紫-緑で
$$1-2\left(\frac{4}{6}\right)^n+\left(\frac{3}{6}\right)^n$$
さぁ、どうでしょうか?一見するとベン図も描けていてよさそうですが、どこに間違いがあったかわかりましたか?
正解は、「オレンジ、紫枠部分は\(\small 1-\left(\frac{4}{6}\right)^n\)、緑部分は\(\small 1-\left(\frac{3}{6}\right)^n\)」の計算です。
Aさんは、例えばオレンジ枠だったら「少なくても3と5が1回出る」の余事象は「3と5以外が出続ける」だから1,2,4,6の4通りが出続ける確率を全体から引けばいいな、と思ったはずです。でもこれだと、「1,2,4,6の4通りが出続ける確率」の余事象は「3か5が含まれる目が出る確率」なので極端に言うと「\(\small n\)回ともすべて3のみ」というパターンも含まれることになります。これだと5が出てないので求めるパターンになりません。
このようなミスが起きるのは、ベン図を描いた後に正しく集合の計算ができずに頭のイメージを頼りに「今回の余事象はこうだ!」と思い込んでしまうことに原因があるので、ベン図をかいたらそれをベースに集合計算に従って計算をすることが非常に大事になります。
まとめ
今回は余事象の問題について2問解説してきましたがいかがでしたか?
余事象は意外と複雑で頭だけで考えるとミスしてしまうこともあるので、ベン図と集合計算をしっかりと行って計算できるように今回の問題をしっかりと復習しておきましょう。
本日はここまでです。お疲れさまでした!





コメント