今回は、2次方程式の応用問題、解の存在範囲を求める問題を解説していきます。
解の存在範囲の求め方
先に結論を言ってしまうと、次の3つを確認することでどんな問題でも解くことができます。
■解の存在範囲の求め方
判別式、軸、境界条件に注目せよ!
- 判別式 ・・・解の個数は?
- 軸 ・・・軸の範囲は?
- 境界条件・・・条件を満たすためには\(\small y\)座標はどうしたらいいか?
では、3つのポイントである、判別式、軸、境界条件をどのように使っていくのか例題を通して確認していきましょう。
異なる2つの正の解を持つ場合
ポイントの「判別式、軸、境界条件」の使い方を例題を通してマスターしましょう。
まず、解の個数から判別式を使います。

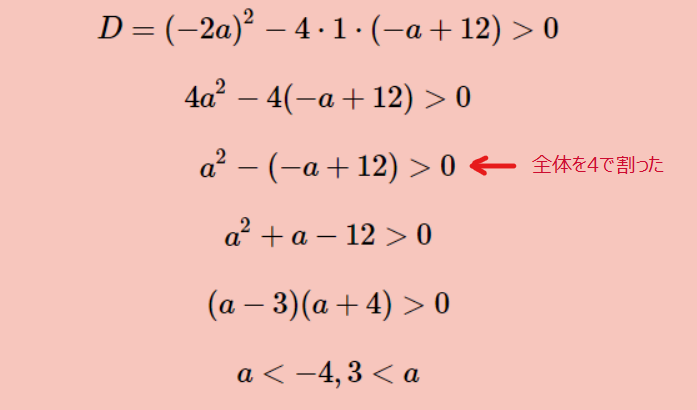
次に、軸と境界条件について考えるために、絵をかきましょう。絵をかかないと、正直、条件を見つけるのしんどいと思います。。。
2次方程式の解と2次関数の関係性は覚えていますか?ここでは詳しく述べませんが、「2次方程式の解」=「2次関数とx軸との交点」でした。なので、今回の問題では、「異なる2つの正の解を持つ」=「2次関数\(\small y=x^2-2ax-a+12\)とx軸との交点が2つとも正」と考えればOK。絵で描くとこんな感じ。
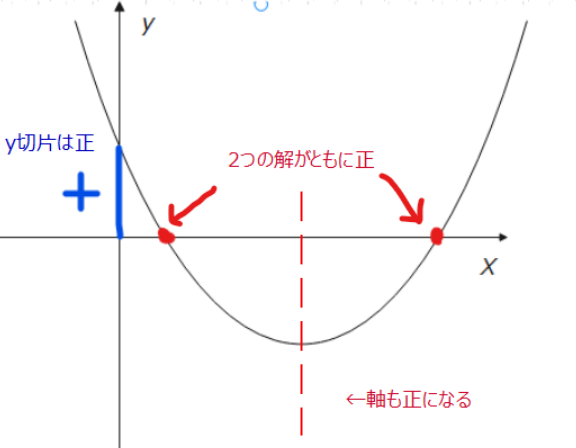
すると、軸と境界条件について以下のような条件があることに気づくと思います。
・軸:常に正になる。
・境界条件:y切片は常に正になる。
(補足)
境界条件について、なんでy切片に注目したのか補足しておきます。
今回は解が正になるという条件があり、解が正かどうかというのは、解がy軸より左側か右側かで決まります。y軸より右にあれば正ですし、左にあれば負です。つまり、y軸が解が正負どちらになるかを決める境目になっているわけです。このような境目のことを数学界では、境界といいます。言葉はあまり覚える必要はないですが、この先境界という言葉を使っていくのでイメージだけ掴んでおいてほしいです。
■失敗しない絵をかく方法
絵を描きましょうとは言ったものの、そもそも絵が間違ってしまう、という人も多いのではないでしょうか?私も、このパターンしかないな、と思っていたら、別のパターンもあったという経験はよくあります。そんな思い込みを防ぐのにおすすめな方法が2つあります。
1つ目は、2次関数をずらしていって、どうなると条件を満たさないのかまで考えておくこと、2つ目は、絵から気づいた条件の妥当性まで考えてみることです。
1つ目は、私はいつも条件を満たさない絵もセットで描いています。
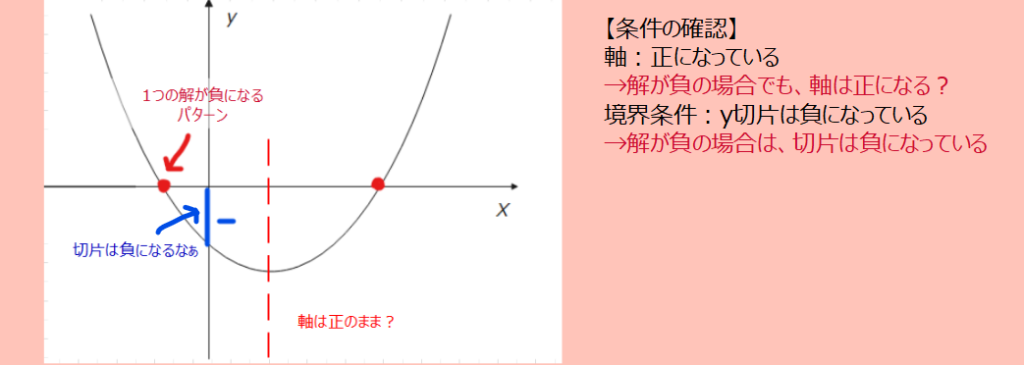
上の図の場合は、軸は正ですが、切片は負になっています。
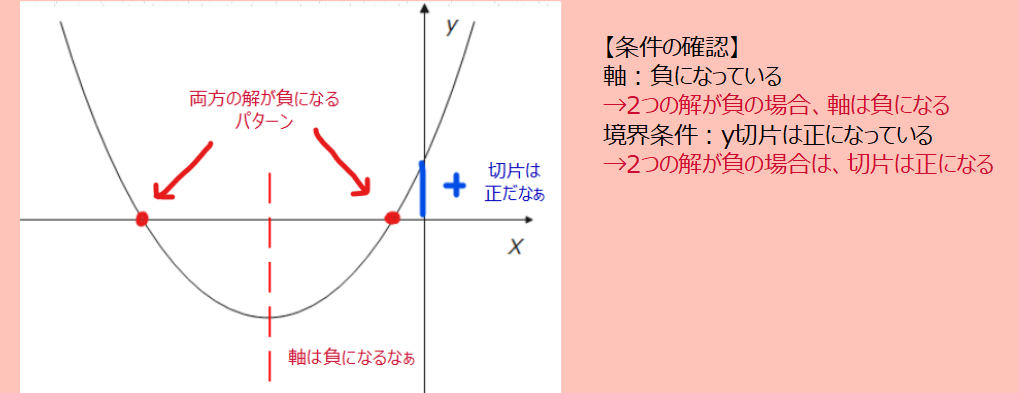
一方で、上の図の場合は、切片は正ですが、軸は負になっています。このように、逆に問題の条件にあてはならない場合も考えてみてあげると、2つの解が正なのは、軸も切片も正の場合でよさそうだな、と判断することができたりします。
2つ目の、絵から気づいた条件の妥当性まで考えるは、少し難しいので余裕があったら確認するでもよいです。今回の例題では、軸も切片も正となる理由を考えてみましょうということです。例えば、軸が正の理由については、軸は2つの解の中間にあり、今回は2つの解がともに正なので軸も正になるとわかるので、絵から気づいた条件は妥当そうだと確信が持てます。
このように、いろいろな角度から理由を探すと思い込みにによるミスは減らすことができるので、参考にしてみてください。
\(\small a>0\)
そして、境界条件はy切片が正なので、切片が\(\small -a+12\)であることから、
\(\small -a+12>0\)
\(\small -a>-12\)
\(\small a<12\)
やっと、判別式、、軸、境界条件の3つの条件がそろったので、最後に条件をまとめます。
①判別式
\(\small a<-4、3<a\)
②軸
\(\small a>0\)
③境界条件
\(\small a<12\)
①~③の条件は、2つの解が正になるための条件を集めてきたものなので、すべて満たす必要があります。1つでも満たせていない条件がある場合、例えば、軸が負になってしまう場合は、途中で紹介した「両方の解が負の場合」になってしまい、今回求める2つの解が正の条件を満たせません。よって、答えはこれらの共通範囲になります。
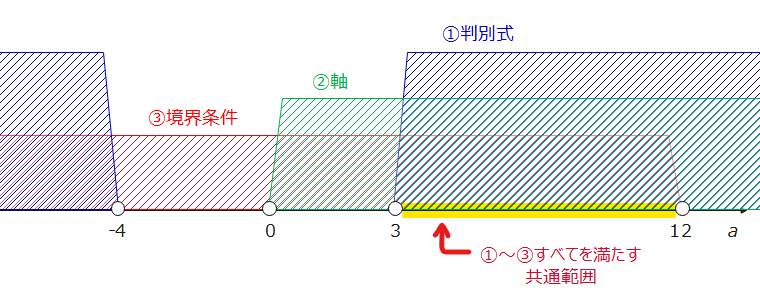
$$\small 3< a <12\space \cdots(答)$$
異なる2つの負の解を持つ場合
異なる2つの実数解を持つので、判別式の条件は、\(\small D>0\)。これを解くと、例題の結果と同じく
\(\small a<-4、3<a\space \cdots①\)
次に、軸と境界条件については、下の絵から
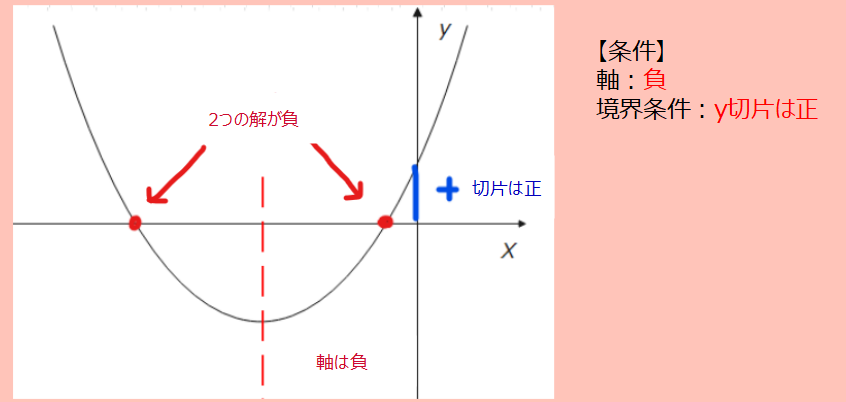
\(\small x<0\space \cdots ②\)
y切片は\(\small -a+12\)であることから、
\(\small -a+12>0\)
\(\small -a>-12\)
\(\small a<12\space \cdots ③\)
①~③の共通範囲は下の図から、
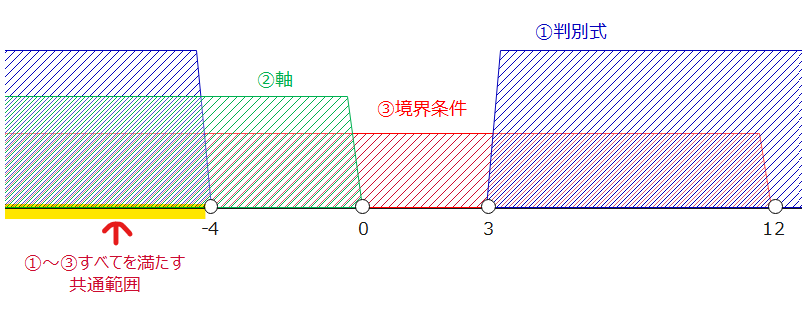
基準値より大きい解と小さい解を持つ場合
実数解の個数は、文章より2個あることが読み取れるので、判別式の条件は、\(\small D>0\)。これを解くと、例題の結果と同じく
\(\small a<-4、3<a\space \cdots①\)
次に軸と境界条件についてはどうなるでしょう。一旦条件を満たすような絵をかいてみます。
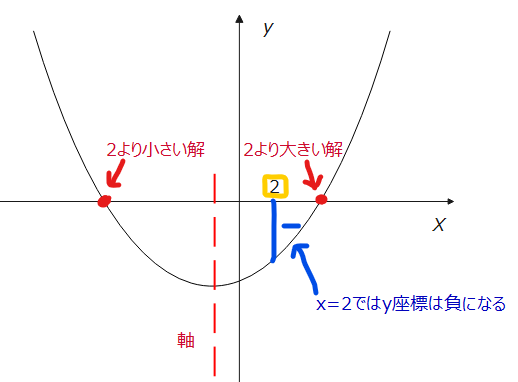
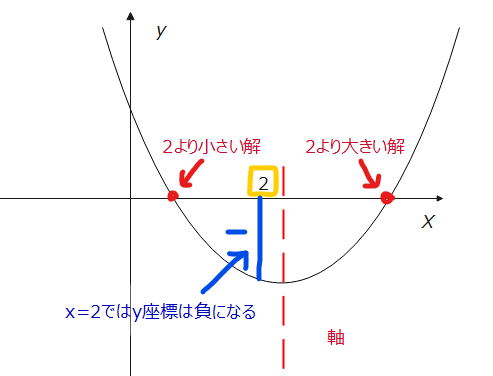
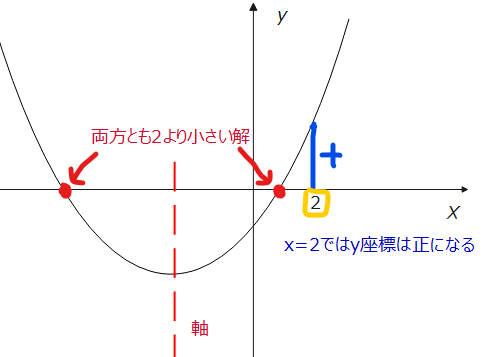
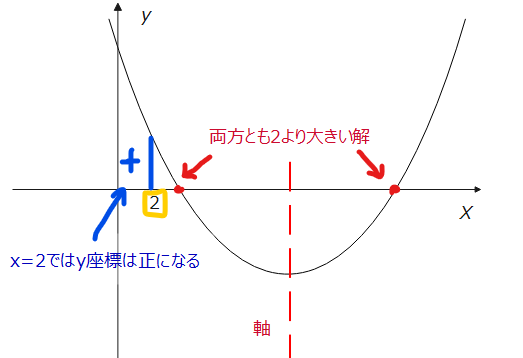
\(\small y=(2)^2-2a・2-a+12\)
\(\small y=4-4a-a+12\)
\(\small y=-5a+16\)
この時の座標が負であればよいので、
\(\small -5a+16<0\)
\(\small -5a<-16\)
\(\small a>\frac{16}{5}\space \cdots②\)
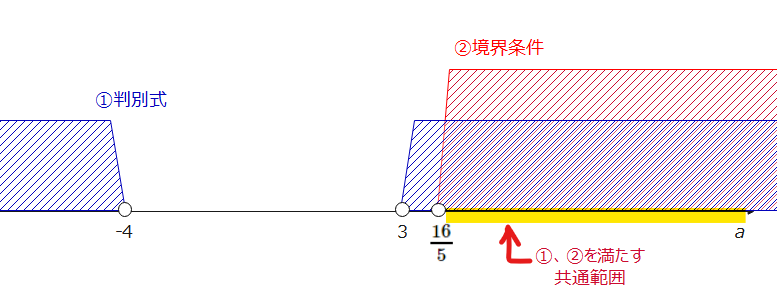
よって、①、②の共通範囲を求めると、
実際の問題での活用例
では最後に、応用問題にチャレンジしてみましょう。
先程までの問題とは見た目が違いますが、少し見方を変えれば同じ問題です。
一見すると、2次関数と直線の交点の問題なので、連立して判別式で解けばいいだろう…、と飛びつきそうです。ただ、直線ではなく、線分となっているので注意が必要かなと思います。まずは毎回恒例の絵をかいておきましょう。
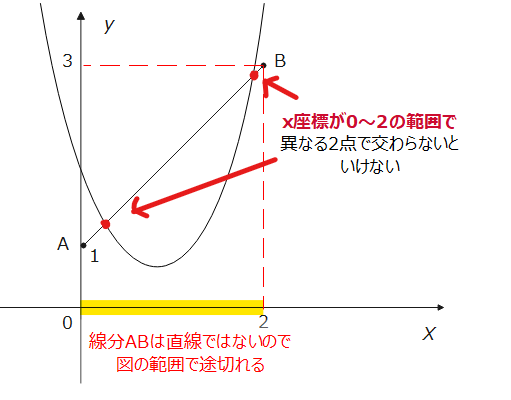
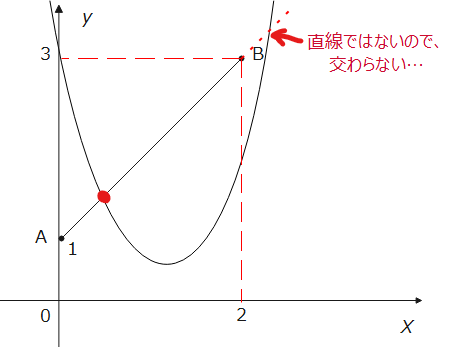

2次方程式、\(\small x^2+(a-1)x+1=0\)が\(\small 0≦x≦2\)に2つの実数解を持つときの\(\small a\)の値の範囲を求めよ。
となります。どうでしょう。さっきまで問題で解いてきた解の存在範囲の問題に帰着しました。では、ここからは同じように、判別式、軸、境界条件に注目して解いていきましょう!
まず、実数解の個数は2個なので、判別式は\(\small D>0\)で、
$$\small D=(a-1)^2-4\cdot 1 \cdot 1>0$$ $$\small (a-1)^2-4>0$$ $$\small [(a-1)+2][(a-1)-2]>0$$ $$\small (a+1)(a-3)>0$$ $$\small a<-1、3<a\space \cdots①$$ 次に、軸と境界条件を考えます。2次方程式、\(\small x^2+(a-1)x+1=0\)が\(\small 0≦x≦2\)に2つの実数解を持つ場合の絵は以下の通り。
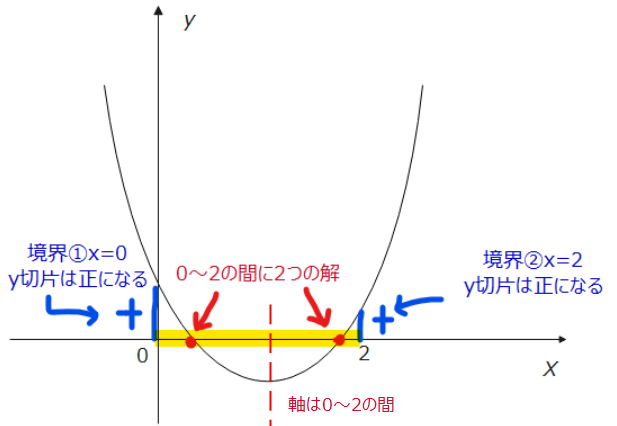
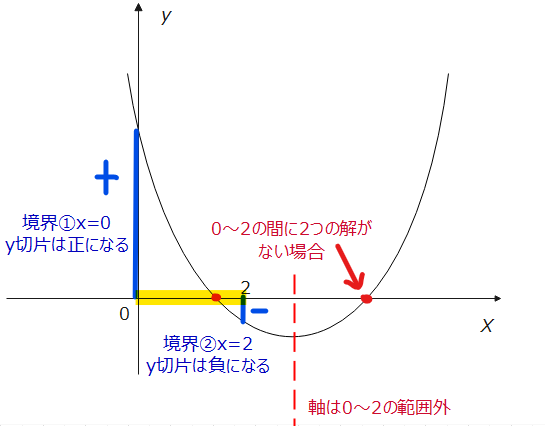
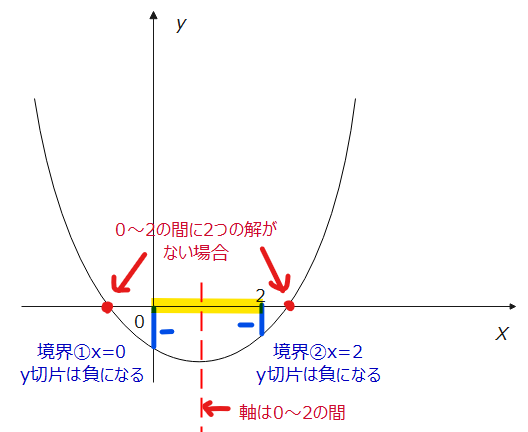
では、軸の条件を数式で表すと、軸が\(\small x=-\frac{a-1}{2}\)であることから
$$\small 0≦-\frac{a-1}{2}≦2$$ $$\small 0≦-(a-1)≦4$$ $$\small 0≦-a+1≦4$$ $$\small -1≦-a≦3$$ $$\small -3≦a≦1\space\cdots②$$ 境界条件は2つあったので、それぞれ考えていきます。まず、境界条件①のx=0でy座標が0以上かについて、x=0のy座標は1なので、実はこれは\(\small a\)の値に関係なく常に満たされているので、OKです。次に、境界条件②のx=2のy座標は、 $$\small y=(2)^2+(a-1)\cdot 2+1$$ $$\small y=4+2(a-1)+1$$ $$\small y=4+2a-2+1$$ $$\small y=2a+3$$ これが0以上になればいいので、 $$\small y=2a+3≧0$$ $$\small y=2a+3≧0$$ $$\small 2a≧-3$$ $$\small a≧-\frac{3}{2}\space\cdots③$$ これで、判別式、軸、境界条件のすべてを見たので、①~③の共通範囲を求めていきましょう。
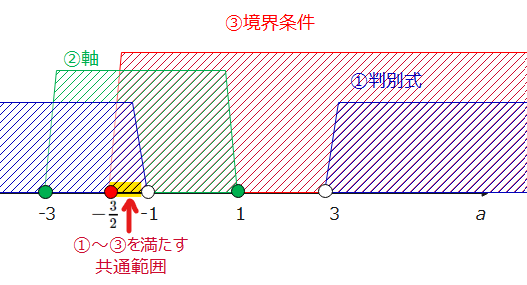
$$\small -\frac{3}{2}≦a<-1\space\cdots(答)$$
まとめ
今回は、2次方程式の解の存在範囲について解説しました。絵をかいて考えるというのが基本になるので、問題集などでいろいろなパターンについて、絵を描くことができるように、練習してみてください。
本日はここまでです。お疲れさまでした!







コメント