「ベクトルって結局、何をしてるのかさっぱり分からない…」 、「公式は覚えたけど、図形が絡むと途端に解けなくなる…」
あなたは今、そんな悩みを抱えていませんか? 数学Cの中でも、多くの高校生が挫折しやすい「ベクトル」。しかし、実はベクトルほど「一度コツを掴めば得点源になる」コスパの良い単元はありません。
この記事では、ベクトルの苦手意識を克服するための具体的な勉強法をステップ形式で徹底解説します。
この記事では、ベクトルに苦手意識がある人でも、苦手を克服できるような勉強法を徹底解説します。
・基礎から独学で伸ばすための3つのステップ
・今のレベルにぴったりの厳選おすすめ参考書
苦手を克服するための具体的な方法について知りたいと思った方は、ぜひ最後までチェックしてください!
ベクトルが全然わからない…と感じていませんか?
ベクトルは、これまでの数学とは大きく雰囲気が異なり、新しい概念の理解が必要ということもあり、そもそもの段階から苦手な人が多い単元です。
- ベクトルの和・差の計算方法が分からない…
- 内積って何?どんな意味があるの?
- 辺の比を求める問題など図形問題にどうベクトルを使えばいいのか分からない…
- 解説を見ても「なぜその式になるのか」が分からない…
このような疑問や悩みを抱えている高校生は少なくありません。
ベクトルの基礎知識で躓いてしまうと、その先の応用問題(ベクトル方程式、平面図形・空間図形への応用等)を解くのは当然難しくなってしまいます。なので、ベクトルが苦手な人はまずはベクトルに出てくる基礎知識をしっかりと理解することが大切です。
ベクトルが苦手な人に共通する3つの原因
【原因①】ベクトルを「式」で理解しようとしている
ベクトルの理解度を図る一番簡単な確認方法は、次の問題に解答できるかを確認することです。
そもそも、ベクトル \(\small \overrightarrow{\mathrm{AB}}\)は、点 \(\small \mathrm{A}\)から点 \(\small \mathrm{B}\)に向かうことを数学的に表しています。
この考え方をもとにすると問題の左辺は『点 \(\small \mathrm{A}\)から点 \(\small \mathrm{B}\)に向かう(下図①)』+『点 \(\small \mathrm{B}\)から点 \(\small \mathrm{C}\)に向かう(下図②)』となり、まとめると、『点 \(\small \mathrm{A}\)から点 \(\small \mathrm{C}\)に向かう(下図③)』と言い換えできます。

最後の『点 \(\small \mathrm{A}\)から点 \(\small \mathrm{C}\)に向かう』は\(\small \overrightarrow{\mathrm{AC}}\)の定義そのものであることから、問題の式が成り立つことが分かります。
皆さんは、うまく説明できましたか?
ベクトルが苦手な人ほど、式だけを見て理解している人が多いです。なので、上記のような問題を出すと、うまく説明できなかったり、「ベクトルの足し算では、\(\small \overrightarrow{\mathrm{A\color{#ff0055}B}}+\overrightarrow{\mathrm{\color{#ff0055}BC}}\)」のように同じ文字がある場合は、最初と最後をくっつけて\(\small \overrightarrow{\mathrm{AC}}\)とすればよい」といった式変形のテクニック的な話をしがちです。
もちろんこのテクニック自体は間違ってなくて計算を早くするためにはぜひ知っておきたいことではあるのですが、なぜそのような方法で計算できるのかを理解していないと延々とテクニックだけを覚えることになり、図形との融合問題を解くときに苦戦することになります。
逆に言えば、『\(\small \overrightarrow{\mathrm{AB}}\)は、点 \(\small \mathrm{A}\)から点 \(\small \mathrm{B}\)に向かうこと』という考え方だけ理解していれば、テクニックの内容は当たり前のことを言っているだけなので簡単に覚えられます。
ベクトルは図形で理解しろ
これがベクトルが苦手な人がまず理解すべきことです。
具体的には…、『\(\small \overrightarrow{\mathrm{AB}}\)は、点 \(\small \mathrm{A}\)から点 \(\small \mathrm{B}\)に向かうこと』と覚えよう。
図形的なイメージを持ってなくても何とかなる問題もありますが、応用問題を解いていきたいなら、図形的に理解しておくことが重要になります。
【原因②】図を描かずに考えている
「ベクトルの問題の解説が分からなんですけど…」と質問に来る生徒の中には、いや図を描けばわかるやん!とツッコミたくなることが多々あります。
ベクトルは図形で理解と言っている以上、図を描かないと解けません。図を描かずにこの問題を解くというのは、例えるなら目隠しした状態で自転車に乗るような行為です。
ではなぜ図を描く必要があるのかですが、今回の問題であれば、そもそも点\(\small \mathrm{P}\)や点\(\small \mathrm{Q}\)がどこにあるのかが図がないとイメージできないですし、そこからベクトル\(\small \overrightarrow{\mathrm{PQ}}\)を求めるには、『点\(\small \mathrm{P}\)から点\(\small \mathrm{Q}\)に向かう』必要があるわけですが、図がないと点\(\small \mathrm{A}~\mathrm{F}\)それぞれの位置関係が掴みにくくどのように辿っていけばいいのかが分からないからです。問題文と一所懸命にらめっこしていてもいい発想は浮かびにくいわけです。
ところが、問題文の条件を図で描いてみると

となり、これを見れば「点 \(\small \mathrm{P}\)→\(\small \mathrm{B}\)→\(\small \mathrm{A}\)→\(\small \mathrm{F}\)→\(\small \mathrm{Q}\)のように辿っていけば点\(\small \mathrm{P}\)から\(\small \mathrm{Q}\)に向かうことができることが分かりやすくなります。これが、図を描く最大のメリットです。
- 問題に書かれた条件を自分なりに図示する
- 図を使ってベクトルの計算をする
これができていない人は、今日から実践してみましょう。
【原因③】難しい問題集で勉強している
ベクトルは最初のハードルが高いため、普通レベルの参考書を買ったつもりでもベクトルの解説に難しさを感じる人は多いです。
- いきなり入試問題を題材にした参考書
- 解説が数式中心で簡潔すぎる参考書
を選ぶと、基礎が固まってないのでなかなか理解が追いつきません。
前章でも述べた通り、ベクトルは図で理解する単元なので「図を使った解説が豊富で、考え方が丁寧に書かれているか」が、参考書選びの際に重要なポイントとなります。
ベクトルが苦手な人の正しい勉強ステップ
【ステップ①】ベクトルとは何かを理解する
そもそもベクトルって何か分からないまま問題を解いている人は意外と多いと思います。でもそれって意味も発音もわからない英単語の綴りを暗記しているようなものなんです。そんな方法でたくさんの英単語を暗記したとしても、実際に英語を読み書きできるようにはなりません。
ベクトルも同じで、そもそもの意味を理解しないまま和・差・定数倍・内積などの公式を全部暗記しても平面図形との融合問題を解けるようにはなりません。なのでまずはベクトルの意味について理解をしましょう。
ベクトルの意味についてはこの記事の【原因①】ベクトルを「式」で理解しようとしているで解説しています。
【ステップ②】ベクトルの和・差・実数倍の計算を「図形的に」理解する
ベクトルが苦手な人が次に身に着けておくべきは、ベクトルの基礎計算を図形的な意味と紐づけて理解することです。ここでは代表例として、和・差・実数倍について紹介します。
【①】ベクトルの和
\(\small \overrightarrow{\mathrm{AB}}+\overrightarrow{\mathrm{BC}}=\overrightarrow{\mathrm{AC}}\)という和の計算は、図形的には『点\(\small \mathrm{A}\)から点\(\small \mathrm{B}\)を経由して点\(\small \mathrm{C}\)まで向かうのは、点\(\small \mathrm{A}\)から点\(\small \mathrm{C}\)へ向かうことに等しい』と理解する。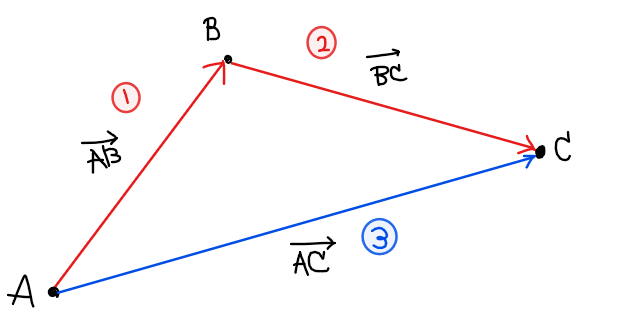
【②】ベクトルの実数倍
実数を\(\small k\)とすると、ベクトル \(\small \overrightarrow{\mathrm{AB}}\)を\(\small k\)倍したベクトル \(\small k\overrightarrow{\mathrm{AB}}\)の図形的な意味は…、
(i)\(\small k≧0\)(正の値)のとき
・ベクトルの長さが\(\small k\)倍になる(向きは変わらない)。
例えば\(\small k=2\)の場合、\(\small \overrightarrow{\mathrm{AB}}\)と\(\small 2\overrightarrow{\mathrm{AB}}\)の関係は以下の通り。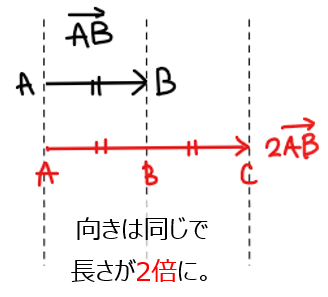
(ii)\(\small k<0\)(負の値)のとき
・ベクトルの長さが\(\small |k|\)倍になり、逆向きになる。
* 絶対値を付けているのは、\(\small k<0\)なので、例えば\(\small -3\)倍みたいに日本語的におかしな表現にならないようにしているだけ。
例えば\(\small k=-1\)の場合、\(\small \overrightarrow{\mathrm{AB}}\)と\(\small -\overrightarrow{\mathrm{AB}}\)の関係は以下の通り。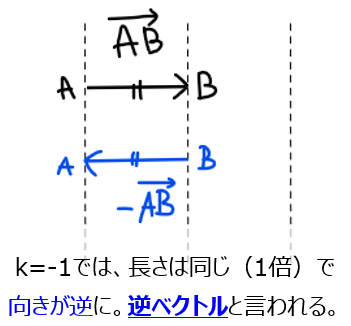
【③】ベクトルの差
ベクトルの差は、『ベクトルと逆ベクトルの和』と理解する。
例えば、\(\small \overrightarrow{\mathrm{AC}}-\overrightarrow{\mathrm{BC}}\)という差の計算は、「\(\small \overrightarrow{\mathrm{AC}}\color{#ff0055}{+(-\overrightarrow{\mathrm{BC}})}\)」の和と考えます。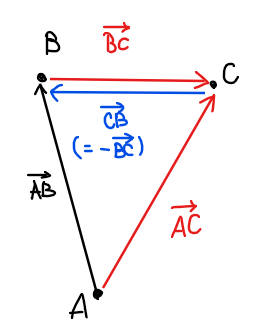
そうすると、【②】ベクトルの定数倍で触れた逆ベクトルの図形的な意味から、\(\small -\overrightarrow{\mathrm{BC}}=\overrightarrow{\mathrm{CB}}\)(逆向きになる)が成り立つので、\(\small \overrightarrow{\mathrm{AC}}+\overrightarrow{\mathrm{CB}}\)。あとは【①】ベクトルの和の考え方から、『点\(\small \mathrm{A}\)から点\(\small \mathrm{C}\)を経由して点\(\small \mathrm{B}\)へ向かう』、すなわち、『点\(\small \mathrm{A}\)から点\(\small \mathrm{B}\)に向かう』と理解できるので、\(\small \overrightarrow{\mathrm{AC}}-\overrightarrow{\mathrm{BC}}=\overrightarrow{\mathrm{AB}}\)と計算できます。
このようなベクトルの和・差・定数倍の計算も必ず図を描いて理解する癖をつけるのが最初のステップです。
ベクトルの問題は基本的には、
- 和
- 差
- 実数倍
の組み合わせです(細かいことを言うと内積がありますが…)。
これを図と式の両方で説明できるようになると、ベクトル演算に関する問題は簡単に解けるようになります。
【ステップ③】典型問題を「図→式」の順で解く
ベクトル演算をマスターできたら、最後は典型問題を図→式の順番で整理して解けるようにしましょう。
- 問題文を図にする
- 図形的な性質を使って必要な辺の比を求める
- 図を使ってベクトルの関係式を立式する
問題によってはベクトルの式だけを見て計算すればよい問題もありますが、多くの問題では図形からベクトルの関係性を考察して、和・差・実数倍を使ってベクトルを求める、あるいは辺の比を求めることが多いです。
この考え方を身につけるには、良質な問題が多く載っている参考書での反復練習が効果的です。
ベクトルが苦手な人におすすめの参考書3選
① ベクトルを基礎から理解したい人向け
『ベクトルが本当によくわかる本 (細野真宏の数学が よくわかる本) 』
・補足説明も豊富でつまづきにくい
・独学でも理解しやすい構成
私自身、受験生時代に苦手分野を克服するためにこの参考書を使って勉強していました。 かっちりした参考書が多い中で、本書の魅力はなんといっても「手書き感」のある親しみやすい見た目です。 また、独学でありがちな「この式変形、どうしてこうなったの?」という疑問も、注釈や補足説明が豊富なので、スムーズに解決できます。数学が苦手な人でも、途中で立ち止まることなく最後まで進められる一冊になっています。
② 入試標準レベルまで引き上げたい人向け
『新課程 チャート式 基礎からの数学C』
・1冊だけで定期テスト~大学入試まで幅広い用途に対応できる
・過去問の橋渡しになる。
高校生なら知らない人はいない代表格の参考書ですね。チャート式はレベル別に白、黄色、青、赤と4つに分かれて、難易度は 白 < 黄 < 青 < 赤 の順に高くなります。なので自分にあったレベルを選択するとよいでしょう。
| 色 | レベル | ターゲット・用途 | 到達目標 |
|---|---|---|---|
| 白 | 入門・基礎 | 数学が苦手な人 教科書を完璧にしたい |
定期テスト・共通テスト準備 |
| 黄 | 標準 | 基礎〜中堅大学を目指す人 平均以上の実力をつけたい |
共通テスト・中堅私大合格 |
| 青 | 応用・発展 | 難関国公立・早慶を目指す人 網羅的に解法を学びたい |
難関校入試の突破 |
| 赤 | 最難関 | 東大・京大・国公立医学部 数学を武器にしたい人 |
最難関校での高得点 |
個人的には数I・Aのときに黄色、青、赤の3冊を持っていました(黄色チャートを買ったつもりが赤チャートだったというミスもあり3冊に…)が、ある程度上位の大学を狙うのであれば青色チャートがおすすめです。赤色は医学部向けということもあり、普段の模試や入試ではあまり見かけないような変わった問題が多いので、医学部を目指しているとかでもなければ不要かなと思います。
あとは注意点として、苦手分野の問題で最初から使うと挫折しやすいので、「ベクトルが本当によくわかる本」→「青チャート」のように、ある程度ベクトルへの理解がついてきてから使うのがおすすめです。
③ 参考書だと長続きしない人向け
スタディサプリ高校講座・大学受験講座(数学)
・動画形式なので、通学中などのスキマ時間で学習できる
・独学のつまずきを解消しやすい
「スタディサプリ高校講座・大学受験講座」は、リクルートが提供するオンライン学習サービスになっており、プロ講師による神授業がPCやスマホなどから簡単に見れるのが特徴です。講義形式なので、参考書を一人で解き進めるのが苦手な人でも始めやすい点が大きなメリットです。
現在の学習状況に合わせて「トップレベル」「ハイレベル」「スタンダード」「ベーシック」の4段階の中から自分自身にあったレベルを選んで授業を受けることができます。
| レベル | 対象・目標 | 内容の特徴 |
|---|---|---|
| トップレベル | 最難関国公立・最私立大学受験対策 | 最難関国公立・私立大学レベルを目指す人向け |
| ハイレベル | 難関国公立・私立大学受験対策 | 難関国公立・私立大学レベルを目指す人向け |
| スタンダード | 定期テスト対策、国公立・私立大学受験対策 | 学校で学んだことの定着度を上げたい人向け 国公立・私立大学を目指す人向け |
| ベーシック | 苦手対策、定期テスト対策 | 教科書レベルの基礎項目をしっかりと学びたい人向け |
「参考書だけでは限界を感じる人」に特におすすめです。
本記事のまとめ
今回はベクトルの苦手を克服するための具体的な勉強法について解説しました。「ベクトル=難しい」というイメージは少しは変わったでしょうか?
最後に、今回のポイントをおさらいしておきましょう。
・ベクトル問題は、図→式の順番で解く
・典型問題の反復演習は、教材選びで理解度が大きく変わる
ベクトルは、一度感覚を掴んでしまえば、驚くほどスラスラ解けるようになる単元であり、そこで身に着けた力は、模試や入試本番でライバルに差をつける可能性を秘めています。
ぜひ今日紹介した勉強法を実践することで、苦手を得意に変えていきましょう。
最後に、本サイトでもベクトルに関する記事はたくさん解説していますので、よければこちらも是非確認してみてください!
今回は以上です。お疲れさまでした!












コメント