領域の色塗分け問題の解法（場合の数）

本記事では、隣り合う領域を異なる色で塗分けする方法が何通りあるのかを求める問題の解き方について解説します。「解き方に自信がない…」、「よくパターンの抜け漏れが出てしまう…」、「解答の解き方も理解できるけど自分の解き方でもよさそうで、どこが間違ってるのかわからない…」などで悩んでいる方は、ぜひチェックしてみてください。

1. 【解説編】色の塗分け問題の解き方

色の塗分け問題にはいくつかの考え方があるので、例題を通して紹介していこうと思います。ぜひ、自分に合った考え方を見つけてみてください。また、それぞれの考え方自体は今後の問題を解くときにも使えるので考え方自体は一通り理解しておきましょう。

6通り

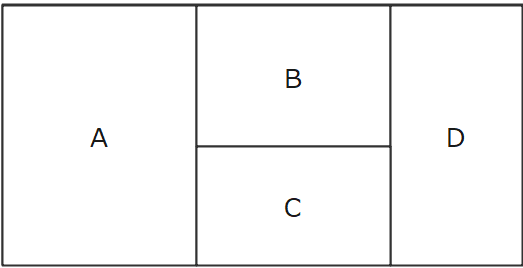
1.1 【解き方その１】樹形図の利用(初心者編)

とにもかくにも、場合の数を求めるときの基本は樹形図を描いてすべてのパターンを漏れなくダブりなく洗い出すことです。この後に紹介する解き方も基本は樹形図を使った考え方が主軸になっているので、場合の数が苦手という人はまずはこの考え方を理解しましょう。

すこし余談ですが、高校生になると順列(\(\small {}_m \mathrm{P}_n \))とか組み合わせ(\(\small {}_m \mathrm{C}_n \))を利用して解くことがほとんどですが、これらは計算方法の手段であって、目的ではないことは忘れないようにしましょう。計算のテクニックを使えれば便利ですが、使い方に不安があるならば、時間はかかるかもしれませんが、しっかり樹形図を描いて全パターンを洗い出した方が確実ですし、樹形図を描けばどんな問題でも解くことができます（もちろん実際は試験時間があったりテストでは\(\small {}_m \mathrm{P}_n \)を使って解けないといけないので勉強しなくていいわけではないですが…）。

では、樹形図を使った解き方の流れを説明します。

1.1.1 【STEP1】色を塗る順に領域番号を付ける

すでに領域にはA～Dまでの名前がついていますが樹形図を描くときには、色を塗っていく順番に領域をナンバリングしておいた方が樹形図を描きやすいので、私は初めに領域番号を付けています。

色を塗るときは、周りと接している領域が多い領域から塗っていくのがおすすめです。なぜならば、そこを先に塗ってしまえば、接している領域は絶対に異なる色で塗らないといけないと決まるからです。

今回だとBとCが3つの領域と接していて最大なので、どちらかから塗っていくのがよいでしょう。ここではBをはじめに塗ることにします。そのあとは、次に接している領域が多いCを塗ります。その次は、AとDも接している領域数は2つで同じなので、どっちから塗ってもよいですが、A→Dの順で塗ることにします。

よって、領域番号はB→C→A→Dの順番に以下の通り付けます。

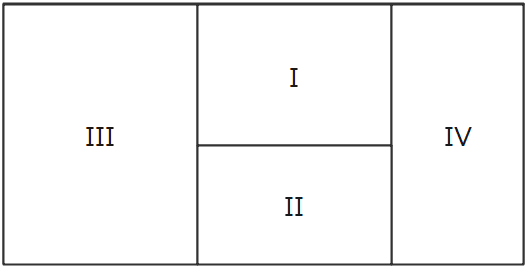
これで樹形図を描く下準備は完了です。STEP2にいきましょう。

1.1.2 【STEP2】同じ色になる領域を意識して樹形図を描く

STEP1でつけた領域番号をもとに樹形図を描いていきます。STEP1で接する領域数が多い領域から番号を付けているので、初めの方は異なる色を塗っていく必要があり分岐はほぼありません。後半にいくにつれて制約が弱まり同じ色で塗ってもよい領域が出てくることなり、ここで分岐が発生します。なので、樹形図の枝を分岐させるときは、同じ色に塗ってもいい領域の組み合わせごとに分けていくようにしましょう。

今回は、領域IIIと領域IVは接していないので同じ色にしてもOKです。それ以外はすべて接している領域同士なので、異なる色で塗らないといけません。それでは、IIIとIVが同じ色になるように樹形図を描いてみましょう。実際に樹形図を描いてみると以下のようになります。

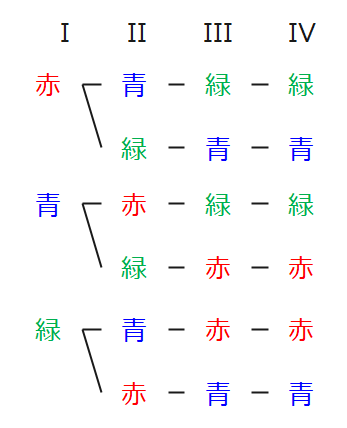
1.1.3 【STEP3】パターンを数え上げる

最後は、STEP2で描いた樹形図のパターンを数えればOKです。答えは、6通りになります。

樹形図を描くことは、漏れがないかやダブりがないかを確認しやすいメリットがある一方で、求めるパターン数が多い場合には描き上げるのが大変になるというデメリットを持っています。このデメリットを軽減するor克服するための方法がこの後紹介する解き方になっているので、しっかり使いこなせるようにしておきましょう！

1.2 【解き方その2】樹形図+順列利用(中級者編)

次に紹介する解き方は、途中までは樹形図を描きつつ、全パターンを描くのはしんどいのである程度パターンが見えたら、そこからは順列の考え方を利用することで全パターン数を求めちゃおうという考え方です。個人的にはこの考え方が一番ミスなくスピードもそこそこ速く解けるのでお勧めです。

では、具体的な解法手順を説明してきます。

STEP1の「色を塗る順に領域番号を付ける」までは同じなので割愛して、STEP2から説明していきます。

1.2.1【STEP2】同じ色になる領域のパターンを樹形図で洗い出す

樹形図を描くときにも意識した点ですが、色の塗分けパターンは大きく分けると同じ領域になるパターンごとに分岐していきます。今回は、領域IIIとIVが同じにあるパターンのみなので、1パーンになります。色も樹形図を描くときは、赤、青、緑と記載していましたが、今回は少し曖昧に、「1」、「2」、「3」としておきます。この少し曖昧にしておくことがSTEP3の順列計算で効果を発揮します。

今回は、同じ色になる領域のパターンを樹形図で描きます。

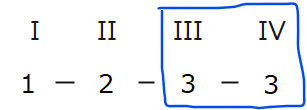
今回は、青枠の部分が同じになるパターンのみです。他にもパターンがある場合は樹形図で描いておきます。

洗い出す際の注意点としては、以下のようなパターンは「領域IIIとIVが同じ色になるというパターン」として同じなのでカウントしないようにしましょう。

1.2.2 【STEP3】パターンごとに順列を使用して計算

最後に、曖昧にしておいた部分を計算して場合の数を求めていきます。

STEP2で、「1-2-3-3」という組み合わせで色を塗ればよいことが分かりました。ここでは1～3に具体的に赤、青、緑の色を割り当てて、場合の数を求めます。ここで出てくるのが順列です。

1～3のに赤、青、緑の色を割り当てる通り数は、1～3に3色を並べるときの通り数と同じなので順列で求めることができます。「赤、青、緑を左から順番に並べる方法は何通りか」という問題と同じということです。

よって、計算式は、\(\small 3!=3 \times 2 \times 1 = 6\)通りと求めることができます。

この方法では、パターン数だけ洗い出せれば、あとは順列計算を使うことで機械的に計算可能なので、解き方その1みたいにたくさんの樹形図を描く必要はありません。ただし、この方法もパターンが多いと結局樹形図を描く量が多くなるので、最後に紹介する解法も参考として知っておきましょう。

1.3 【解き方その3】順列利用（上級者編）

最後に紹介する解き方は決まった手順があるわけではないので、「こんな解き方もあるんだなぁ」と参考程度に読んでもらえればと思います（といっても解き方自体は解き方その2とほぼ変わりません）。

まず、A～Dの領域を問題の指示通りに塗り分けるためには、AとDが同じ色になる必要があります。AとDに塗る色は赤、青、緑の3通り、残りの2色をBとCに塗れればよいので計2通り。よって答えは、\(\small 3\times2=6\)通りと求まります。

いかがでしたでしょうか？あっさり求められる分、図がないのでイメージがわかないという人もいたかもしれません。逆にこの解き方の方がしっくり来たという人もいたと思います。

補足としてこの解き方で解く場合は、初めの方でパターンの洗い出しが漏れると大きく答えがずれてしまうのでっ注意が必要です。また、イメージ図がなく直観的に解いている部分もあるため、実は重複したパターンが混じっていたとしてもなかなか気づきにくいというのがデメリットです。なので、慣れないうちは、解き方その1かその2で解いていき、ある程度自信がついてきたら、その3の方法でも解けるようになっておくといいかなと思います。

1.4 他にも解き方はたくさんある

ここでは、領域の塗分け問題の解き方について、初心者編、中級者編、上級者編の3つに分けて紹介しましたが、もちろん他にもたくさんの解き方があります。でも、枝葉の違いはあれど、大枠はこの3パターンに分類されると思うので、苦手な人はまずはこの3つの考え方を理解できておけばokです。そのうえで、ぜひ自分に合った解き方やカスタマイズを楽しんでみてください。

1.5 ビジネスでも使える樹形図

少し余談ですが、樹形図はビジネスの世界でもよく使われるツールです。たとえば、原因を特定するときや課題の解決策を検討するときなどで使います。

具体的な例として、「とあるコンビニ店舗の売上を伸ばすにはどうしたらいいか」という課題を考えるとしましょう。コンビニ1店舗の売上は、細かい要素はわきに置いておくと、とてもざっくりいってしまえば、

$$売上=(来店客数)\times(購入率)\times(平均客単価)$$

で決まります。なので、売上を上げたいと思ったら、来てもらうお客さんを増やすか、商品を買ってもらう確率を高めるか、買ってもらう商品の値段を上げるかの大まかには3択になるわけです。

ここで、来てもらうお客さんにはどんな人がいるかを樹形図で洗い出してみます。

こんな風に樹形図を使って漏れなくダブりなく洗い出していくことで、ターゲット層を俯瞰してみることで、「うちのコンビニの近くに高校があったから、高校生をメインターゲットにして学割キャンペーンを実施したらいいのでは？」などの解決策が見えてきたりします。

もちろん、ビジネスで使う樹形図は数学の樹形図とは違ってただ一つの正解があるわけではありません。その時代の前提条件（世論、流行・トレンド）や課題解決をするときのアイデア次第でいくつもの正解があります。そこが、ビジネスの難しいところでもあり、興味深い部分でもあります。

2. 【演習編】領域塗り分け問題

では、解法編で学んだ解き方を使って領域塗り分け問題を解いてみましょう。

2.1 特定数の色で塗り分ける（基本問題）

48通り

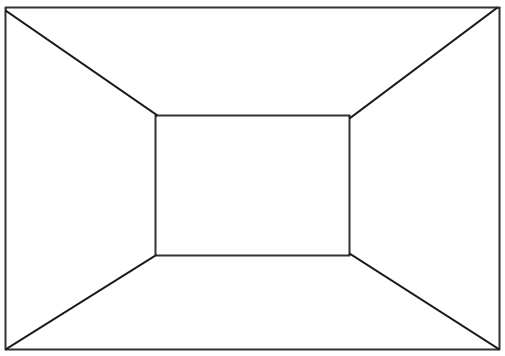
今回は、個人的におすすめの解説編「解き方その2」でお伝えした方法で解いていきます。

まずは、領域に番号を振っていきます。一番初めに塗るべきは、接している領域数が最も多い中央部分です。そのあとは、どこも同じなので、以下のように順番を付けておきましょう。

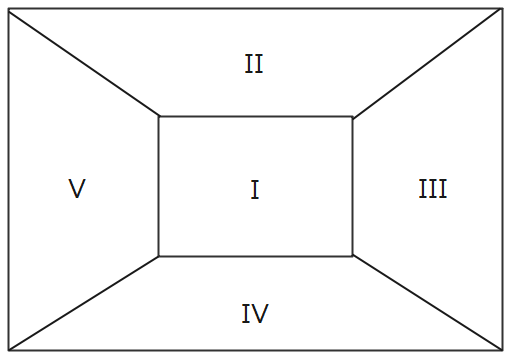
この問題では4つの色をすべて使うので、どこか2つの領域が同じ色になるはずです。同じ色になる領域のペアでパターンを洗い出ししていきましょう。

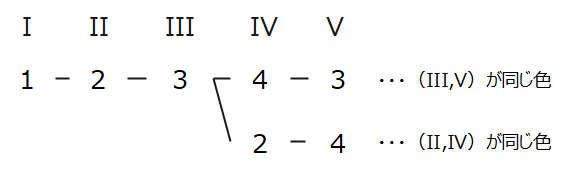
樹形図を描くと、領域IIIとVが同じになるパターンとIIとIVが同じ色になるパターンの全2パターンがありますね。

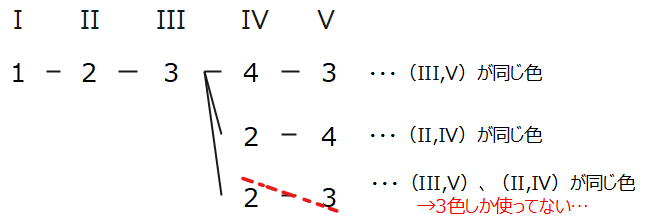
領域の塗分けパターンが2パターンだとわかったので、それぞれの順列計算をしてきます。（1,2,3,4,3）のパターンは、1～4の箇所に4つの色を並べていけばいいので、\(\small {}_4 \mathrm{P}_4 =4!=24\)通り。（1,2,3,2,4）のパターンも同じく24通りあるので、2つのパターンを足して、48通りが答えになります。

最後にそれぞれのパターンを足すのか掛けるのか迷った人は、「積の法則、和の法則の使い分け（場合の数、確率）」で解説しているので、こちらもチェックしておきましょう。

2.2 いくつかの色を使って塗分ける（標準問題）

540通り

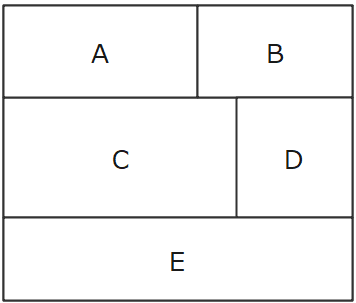
一見すると2.1の問題と同じように見えますが、明らかに違うのが「5色以内」という部分ですね。5色全部使って塗分けてもいいし、4色だけ使って塗分けてもいいということ。なので何色使うのかで場合分けしながら解いていきます。今回は解説編「解き方その2」で解説した後に、別解として「解き方その3」で解いていきます！

まずは色を塗る順番ごとに領域にナンバリングしていきます。微妙に境目がずれているので境界線に沿っていくつの領域と接しているか丁寧に確認してあげましょう。

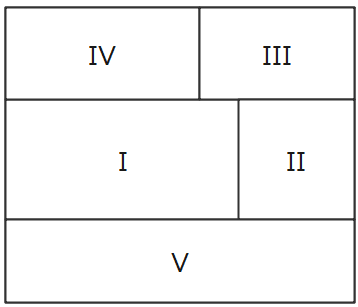
[1]5色全部を使う場合

これは簡単で、5色を領域I～Vに並べる順列なので、5!=120通り…①

[2]4色を使う場合

同じ色になる領域を洗い出すと以下の通り。

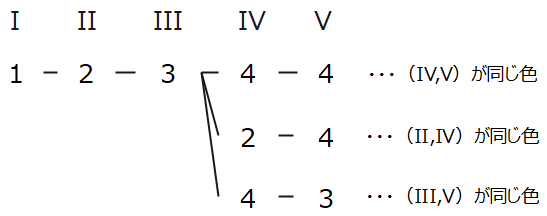
これらの塗分けパターンは、いずれも5色から4色選んで並べる順列で求められるので、\(\small {}_5 \mathrm{P}_4 =120\)通り×3パターン（樹形図で求めた塗分けのパターン）=360通り…②

[3]3色を使う場合

塗分けのパターンは、以下の1通りだけしかありません。

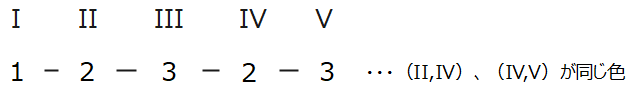
よって、求める場合の数は、\(\small {}_5 \mathrm{P}_3 =60\)通り…③

2色以下では問題の条件を満たすような塗分けは不可能。

よって、①～③より、求める場合の数は、それぞれの場合を合わせて120+360+60=540通り。

5つの領域を塗る順番に領域I～Vにナンバリングするところまでは同様。領域Iから順番に色を塗っていくことを考える。

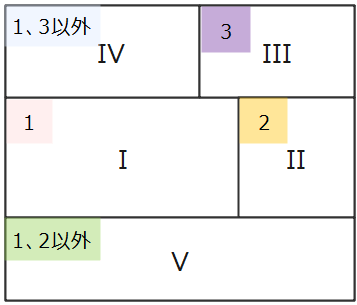
まず、領域I～IIIには5色から異なる3色を選んで塗ればよいので\(\small {}_5 \mathrm{P}_3 =60\)通り(仮に選んだ色をそれぞれ「1」、「2」、「3」とする)。次に領域IVに塗る色は、5色のうち接している領域I、IIIとは異なる色（「2」、「４」、「5」）であればのどれを塗ってもokなので、5-2=3通りの色を塗ることが可能。同じく領域Vについても3通りの色が塗れるので、求める場合の数は、60×3×3=540通り。

2.3 立体を塗り分ける（応用問題）

最後は応用問題です。

この問題は難易度も高く、解説を書いていたら長くなってしまったので、「ゆっくり雑談」の方の記事で解説します。余裕がある人や興味がある人は解いてみてください。この分野が苦手な人はこの問題はスキップで大丈夫です。

解説はこちら→正十二面体を4色で塗り分ける方法（立体の色塗り分け問題・場合の数）

3. まとめ

今回は、場合の数を求める問題の中で領域の塗り分け問題の解き方を解説しました。解き方は大きく3種類あって、樹形図を使って全パターンを洗い出す解法、樹形図と順列計算を組み合わせる解法、順列計算だけで解く解法でした。自分に合った解き方やカスタマイズをしながら演習問題は解けましたか？

いろいろな問題を解くことで経験値がたまり解説の意味が分かるようになることもあるので、他の問題もたくさん解いてみてください。

それでは今日はここまでにします。お疲れさまでした。