本記事では、順列問題の中でも「人を一列に並べる(隣接させる/させない)」、「数字を並べる」問題に関する場合の数の計算方法について解説します。「どう考えたらいいかわからない」、「抜け漏れなく数え上げる方法が知りたい!」、「順列に苦手意識がある…」という人に向けた記事になっていますので、一つでも当てはまるものがあれば、ぜひ最後までチェックしてみてください!
1.【導入編】そもそも順列とは
1.1 順列の意味
初めに今回のメインテーマである「順列」について説明しておきます。「順列」とは一言でいうと「順番を付けて並べる」ことです。「1、2、3」の3枚のカードを順番に並べるのが順列だということです。
ここで一つ誤解してほしくない重要なポイントがあります。それは、順列とは計算方法の名前ではないということ。だから必ずしも\(\small {}_m \mathrm{P}_n\)のような計算をしないと解けないわけではないというのは覚えておきましょう。順列と聞くと「あのPとか使う計算するやつか…」と拒否反応が出て途端に難しく考えてしまう人がいますが、計算で考えるのが難しければ、基本に立ち返って「樹形図を描く」方法で通り数を求めればよいだけです。樹形図で考えていくうちに、実は自然と計算の方法を身に着けることができます。
1.2 順列の具体例
順列とは並べ方だと説明しました。数学の問題では、何を並べるのかでいくつかの種類があります。「人を並べる」、「数字を並べる」、「アルファベットを並べる」などが典型的です。
これだけを聞くと「順列って何かを順番に並べるときしか使えないんだー」って思う人もいるかもしれませんが、その考え方は半分正解で半分不正解です。正確には、「順番に並べる」という考え方が当てはまるようなものも順列と呼ぶことがあります。
具体的には、「ある条件を満たす整数の個数を求める問題」や「アルファベット順に並べたときに何番目に来るかを求める問題」、「領域に色を塗っていくパターン数を求める問題」なども順列に分類されます。これらの問題では、実際に何かを並べているわけではないのですが、便宜的に「数字やアルファベット、色を並べてあげる」と考えると解くことができるので、順列とみなすわけです。
今回は、「人を並べる」、「数字を並べる」問題についてこの後詳しく解説していきます。
2.【解説編】順列問題の解き方
2.1 順列計算の基礎知識
具体的な問題の解説に入る前に、これだけは知っておいてほしいという順列計算の基礎知識を2つだけお伝えしておきます。
- m個の中からn個を選んで1列に並べる方法は、\(\small {}_m \mathrm{P}_n\)で求める。

- m個のものを適当に1列に並べる方法は、\(\small m!\)で求める。

では、2つのポイントについて解説していきます。この2つは多くの問題でほぼ確実に使う考え方なので絶対に覚えておきましょう!
2.1.1 m個の中からn個を選んで1列に並べる方法は、\(\small {}_m \mathrm{P}_n\)で求める
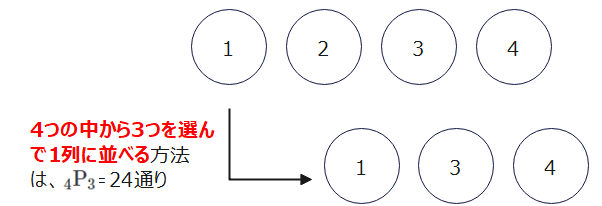
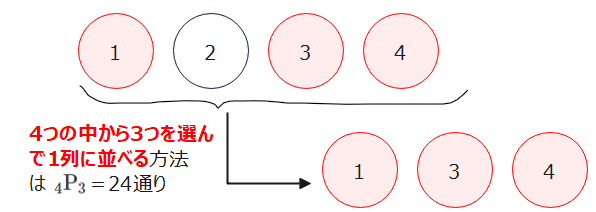
\(\small {}_m \mathrm{P}_n\)という記号が出てくると、「なんだか難しそう…」と思ってしまう人もいるかもしれないですが、計算方法自体はとっても簡単です。文字が入るとややこしいの具体的な数字で計算の仕方を覚えましょう。\(\small {}_4 \mathrm{P}_3\)を計算しようと思ったら、先頭の「4」から4×3×2と「3」つを掛け算しなさいという意味です。
つまり、1つ目の順列計算の基礎知識で言っているのは、4個の中から3つを選んで1列に並べる方法は、\(\small {}_4 \mathrm{P}_3=4\times3\times2=24\)通りと求めればいい、ということです。
これは4つのものを仮に、A、B、C、Dとおくと、3個を並べるときに、1つ目にはA~Dの4通りの中から選ぶので4通り、2つ目を選ぶときは、1つはすでに選んでいるので、残りの3つから選ぶので3通り、最後の3つ目も同様に、残り2つの中から選ぶので2通りとなるので、4×3×2=24通りという中学で学んだ場合の数の計算の考え方そのものです。
これを記号で一言で表すと「\(\small {}_4 \mathrm{P}_3\)」になるというだけのことなので、あまり難しく考えないようにしましょう。
2.1.2 m個のものを適当に1列に並べる方法は、m!で求める
これは1つ目のポイントの特殊バージョンで、先程はm個の中からいくつか選んで並べていましたが、今回は、全部を並べてしまうということです。
全部を並べるということは、1つ目のポイントに無理やりあてはめて言い換えるならば、m個の中からm個を選んで並べるということなので、\(\small {}_m \mathrm{P}_m = m!\)ということです。
なので2つの基礎知識があるといったのですが1つ目の基礎知識を持っていれば2つ目は覚えなくてもOKです。ただ、よく使うのでここではあえて紹介しておきます。
2.2 順列問題の解き方の指針
今回は、順列問題の中でも私が考える「人を1列に並べる」、「数字を並べる」問題に共通する解き方の指針を紹介します。
ではそれぞれ説明していきます。
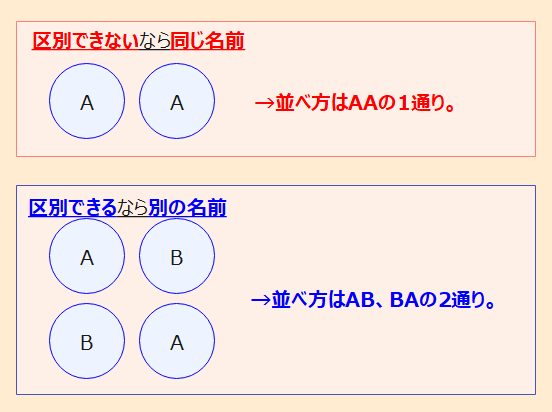
2.2.1 【STEP1】区別するかしないかを意識してものに名前を付ける
突然です、以下の問題は解けますか?
(2)異なる青玉2つを1列に並べる方法は何通りか。
答えは、(1)は1通り、(2)は2通りです。ここで言いたいのは、「区別するものとしないもので通り数が異なるので、まず初めに区別する必要があるのかどうかが分かるように名前を付けてしまおう」ということです。
(1)は「見た目が同じ」とあるので同じ名前、(2)は「異なる」とあるので区別できる名前が必要です。問題文で番号やアルファベットが振られていない場合は、初めに数字やアルファベットで名前を付けて区別できるようにしておきます。
2.2.2 【STEP2】順列計算が使えそうか判断
順列の問題なのに順列計算が使えるかを判断するというのはおかしな話に思えますが、中には順列を使えば解けそうだけど、考えだすと順列計算が複雑になる場合があります。たとえば、規則性があまりなかったり、並べ方が複雑なものは順列計算で考えることが難しくなる傾向があります。
こういう場合は、順列計算はあきらめて、基本的考え方である樹形図を描くことで解いていきましょう。これが、「1.1 順列の意味」で「順列は計算方法の名前ではない」と伝えた意図です。順列の問題をやっていると「この問題、順列計算を使ってどう解けばいいんだろう…」という思考に陥りがちですが、順列計算の方法に悩む問題はそもそも順列計算を使って解くことができないことが多いので、どうやって順列計算するのか考えたところで意味がないです。英和辞典を使ってドイツ語の意味を調べようとしても絶対に調べられないのと同じです。目的に合った手段を見極めて使うのが大事だということです。
遭遇する頻度は高くないと思いますが、たまにこういう問題も混ざっているので気を付けておきましょう。
2.2.3 【STEP3】条件に対して箱を作って並べる(順列計算の基礎知識を活用)
最後のステップは「条件に対して箱を作って並べる」です。どういう意味かよくわからないと思うので具体例で説明してきます。
例えば、「5人の部員の中から部長、副部長を決めるとき、部長と副部長の選び方が何通りあるか」を考えるとき、私は、条件である「部長、副部長」に対して「部長の箱」と「副部長の箱」を作って、その箱にに5人の部員を2人選んで入れるという考え方をしています。
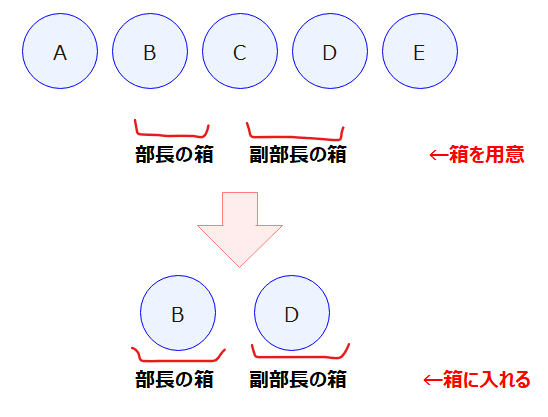
「箱を作る」というのは私が個人的に使っている表現なので、皆さんがイメージしやすいものに置き換えてもらって大丈夫です。大事なのは、「入れ物」を作ってあげてそこに並べていくというイメージを持つことです。
そして、箱に入れるときには「2.1 順列計算の基礎知識」でお伝えした、2つの考え方を使って並べてあげればOKです。
上の例では、5人の部員の中から2人選んで部長と副部長の2つの箱に1列に並べればよいので、\(\small {}_5 \mathrm{P}_2 = 5\times4 = 20\)通りと求めることができます。
3.【演習編】パターン別順列問題
では、解説編で学んだことを演習問題を通してアウトプットしていきましょう。
3.1 【問題①】人を1列に並べる問題
男女交互に並べるとなると、並べ方は、「男女男女男」しかありません。「じゃあ答えは1通り!」ではないので注意。解説編のSTEP1で書いた「区別するかしないかを意識してものに名前を付ける」をすっ飛ばすとこういうミスにつながるので、同じミスをした人は、まずはここを気を付けましょう。
今回は、男子3人、女子2人はそれぞれ別々の人ですから区別して並べてあげる必要があります。ここでは、男子をA、B、C、女子をD、Eとしておきましょう。
次にSTEP2として、順列計算が使えそうかを考えます。実際に問題を解くときにはSTEP3の箱に並べる作業をする段階でできそうかどうか判断することになるので、まずはできる前提でSTEP3に進んでいきましょう。
では、STEP3として条件となる箱を考えます。今回は並べ方の条件である「男女男女男」の箱を作って、そこに並べてあげます。
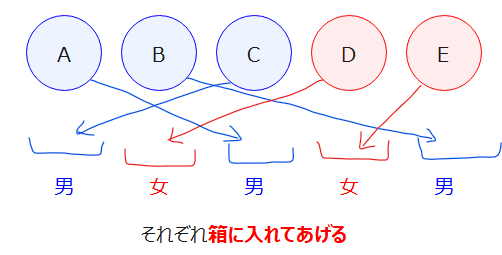
ここで、男子を箱に入れることに注目すると、交互になっていれば並べ方は適当でよいので、「3つものを適当に1列に並べる」考え方が使えます。よって、その通り数は、3!=6通りです。…①
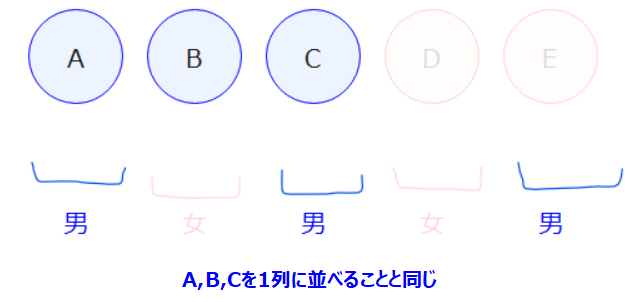
女子についても同様に考えると、2人を1列に並べればよいので、2!=2通りです。…②
①,②から、男女交互の並び方は、6×2=12通りと求まります(step2で気にしていた順列計算はできましたね)。
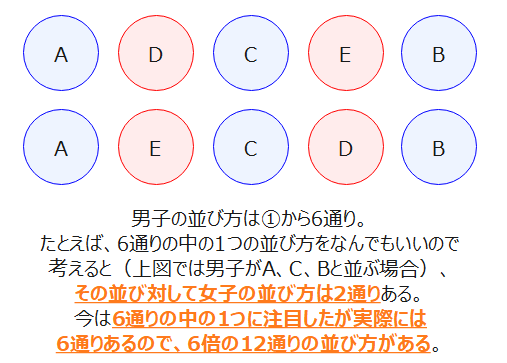
最後の計算で、①と②を掛け算するのは、男子の並び方それぞれに対して女子の並び方が2通りずつあるからです。詳しくは「積の法則、和の法則の使い分け(場合の数、確率)」で解説しているので、求めた通り数を掛け算するのか足し算するのか不安だなと感じた人は、ぜひ確認してみてください!
3.2 【問題②】隣接する/しないように人を1列に並べる問題
(1)男子A、Bが隣り合う
(2)女子が隣り合わない
(2)1440通り
今回は問題文中に男子と女子の名前が区別されているのでSTEP1は省略できますね。
STEP2として順列を使えるかの判断ですが、隣接する/しないように並べる問題は順列計算で求めることができます。なのでSTEP3に移っていきます。
では、ここからが本題です。「男子A、Bが隣り合う、他の人は適当に並ぶ」が問題の条件なので、この条件を箱にします。
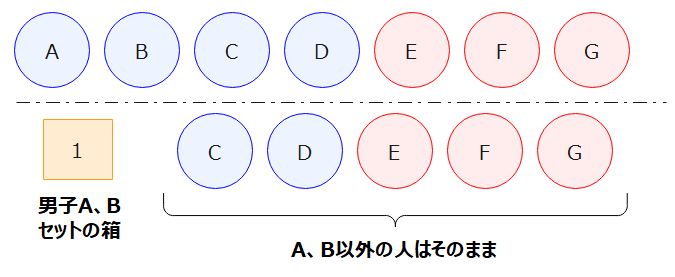
上図のように、男子A、Bが隣り合うという条件に対して「男子A、Bセットの箱」を作ります。この中にA、Bを入れる感じです。一方でそれ以外の5人は1列に並べればいいので、箱は作らなくてOKです。
あとは、箱に人を入れていけばOKです。
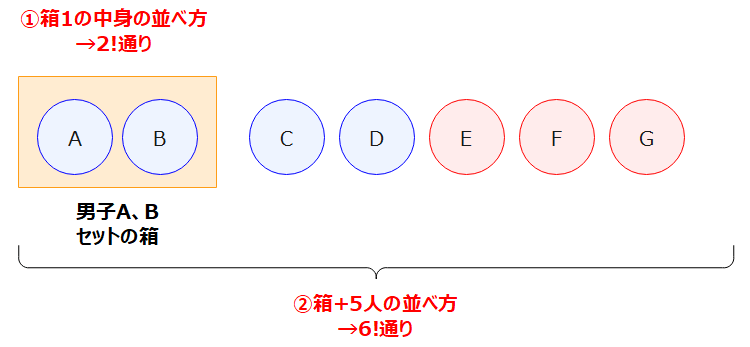
まずは、箱の中身の並べ方ですがA、Bの2人を適当に並べるので2!=2通り…①。次に、箱とC~Gの5人をごちゃまぜに並べます。この並べ方は、6個のものを適当に並べることなので、6!=24通り…②。
よって、積の法則から①と②の場合の数をかけ合わせて、2×24=48通り。
STEP1、2は(1)と同様なので割愛します。
STEP3の条件の箱作りですが、「隣り合わないようにする=隙間に入り込む」と考えます。つまり、男子が並んだ隙間に女子が並んでいくと考えます。
「男女男女男女男」は女子が隣り合わない並び方の一部分にすぎません。女子が隣り合わないのであれば、例えば「女男男女男女男」などもOKなわけです。
このように思いついたパターンが、実は全体の一部でしかなく他にもパターンがあったということは、ぱっとした思い付きベースで考えてしまうと発生しやすいです。
このような考慮漏れを防ぐためには、思いつきだけではなく、他にも条件を満たす並べ方がないかを一度落ち着いて考えることが大切です。ただ、それでもほかの可能性に気がつかないことはあると思うので、いろいろな問題を解いてある程度パターン化しておくことも大切です。
男子を並べるための箱と女子を並べるための隙間をセットします。
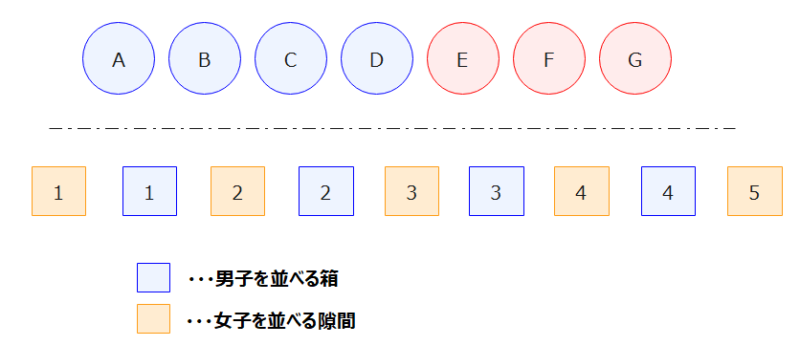
上図で、青色の箱に男子4人を並べる方法は4!=24通り、女子は男子がいる隙間に並ぶようにすれば隣り合わないので、オレンジ色の5箇所の隙間のうち3箇所を選んでE、F、Gを並べればよいので、\(\small {}_5 \mathrm{P}_3 = 5 \times 4 \times 3 = 60\)通り。よって、全体の並べ方は、24×60=1440通りとなります。
3.3 【問題③】数字を並べる問題
(1)3桁の整数
(2)3の倍数
(2)10通り
STEP1はすでに数字が区別されている、STEP2はいったん順列で解く方向で考えてみます。
STEP3は、3桁の整数を考えるので、百の位、十の位、一の位の箱をそれぞれ書いておきます。
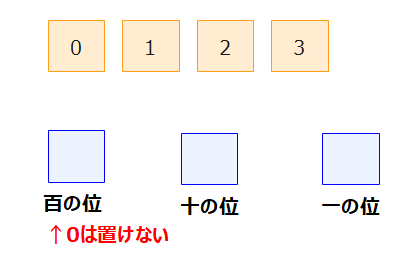
百の位には0は来ない(「023」とかは3桁の整数ではないので)ので、0以外の3通りがあります。十の位と一の位には、0も含めて残りの3つから2つを選んでおいてあげればよいので、\(\small {}_3 \mathrm{P}_2 = 3 \times 2 = 6\)通り。よって、全体では、3×6=18通りの並べ方があるので、これが3桁の整数の個数になります。
STEP1は(1)と同様なので割愛。STEP2は人によっては順列計算は難しいと判断した人もいるかもしれません。樹形図を描いても解けるのでそれでもOKですが、順列計算できる部分もあるので今回はその方法で解いていきます。
箱の作り方は(1)同様ですが今回はその箱にどのような値を入れるのかがポイントです。3の倍数には「各桁の数字を足した数が3の倍数になる」という特徴があります。例えば、123は「1+2+3=6」で6は3の倍数なので、123も3の倍数だと判断できます。この特徴をもとに3桁に設定され得る数字のパターンを洗い出していきます。
パターンを洗い出すときには、抜け漏れを防ぐため、なるべく規則的に洗い出していきます。洗い出しをするときには、注意点として、数字の組み合わせだけを一旦洗い出します。組み合わせが分かればそこから並べるときに順列計算を使えるため。私は洗い出しをするときは、数字が小さい順になるように洗い出していきます。
まずは、各桁を足して「3」になるパターンを考えると、(0,1,2)、次に各桁を足して「6」になるパターンは、意外とないのですが、(1,2,3)が合計で6になります。
ちなみに、(1,0,2)などは数字が小さい順に洗い出すパターンに反しているので、このようなパターンは考えません。なぜならば、(0,1,2)でパターンを洗い出ししているからです。
参考までに私がこの問題をつくときにパターンの洗い出しをした際のメモを載せておきます。

さて、これまでの結果を整理すると今回3の倍数になる桁の組み合わせは、(0,1,2)と(1,2,3)の2パターンのみ。ここから、並べ方の総数を確認します。
まず(0,1,2)は、百の位には0は設定できないので、1、2の中から1つを選んでおくので、\(\small {}_2 \mathrm{P}_1 =2\)通り。残りの十の位と一の位は残りの2つを並べればいいので2!=2通りなので、全体では、2×2=4通り…①。
次に(1,2,3)は百の位、十の位、一の位のすべてに適当に置くことができるので、3!=6通り…②。
①、②は別々のパターンなので、和の法則から、4+6=10通り。
3.4 【問題④】完全順列
問題文中に果物の名前でそれぞれ区別されているのでSTEP1はクリアです。
次に、STEP2の順列計算が使えそうかについて考えます。果物の名前が長くて煩雑なので、みかん、りんご、ぶどう、いちごをそれぞれ1、2、3、4とします。今回考える順列は、1の箱には1以外が入り、2の箱には2以外が入り…という順列です。
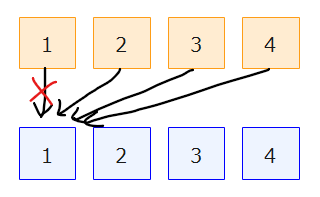
まともに順列計算で考えると、まず1の箱に入れることができるのは2~4の3通り。次に、2の箱に入れることができるのは、1の箱に2を入れた場合は、残りの1、3、4の3通りですが、1の箱に入れたのが2以外(3か4)の場合は、2は入れることができないので、2通り…と考えていく必要があるので、かなり複雑な場合分けが必要そうだとわかります。
このような場合は、まとめて計算する手法である順列計算は合わないので、樹形図を描いてパターンを洗い出すのがよいでしょう。樹形図を描いてみると以下のようになります。

よって、9通りあります。
今回のように1の箱には1以外、2の箱には2以外のように、nの箱にはn以外を入れていく順列のことを「完全順列」といいます。
解説では順列計算は複雑なので樹形図を描いて求める方法を紹介しましたが、実は少しテクニックを使うと計算を使用して求めることができます。
考え方としては、「①単純に4つの数字を4つの箱に適当に入れた場合の数」から「②最低どれか一つでも箱の数字と入れた数字がかぶってしまう場合の数」を引き算すれば残るのは「③箱の数字と入れた数字がかぶらない場合の数」になります。③が今回求めたい場合の数ですね。
①は、4!=24通りで簡単に計算できます。問題は②です。ここで使うテクニックとしては、集合の分野で習う「和集合の要素の個数」の公式です。
・\(\small n(A \cup B \cup C) = n(A)+n(B)+n(C)-n(A \cap B)-n(B \cap C)-n(C \cap A) \)
\(\small +n(A \cap B \cap C) \)
詳しい証明は長くなるので割愛しますが、公式のポイントとしては、まずは単純にそれぞれの要素の個数を合計し(\(\small n(A)+n(B)+n(C) \))、そのあと2重に計上している分を引き算し(\(\small -n(A \cap B)-n(B \cap C)-n(C \cap A) \))、最後に引きすぎた部分を足しこむ(\(\small +n(A \cap B \cap C) \))という公式です。
この考え方は4つ以上の場合にも使える公式なので、この公式を使用して「②最低どれか一つでも箱の数字と入れた数字がかぶってしまう場合の数」を計算してみます。
今回の場合であれば、まず1の箱に1の数字が入っていしまう、2の箱に2の数字が入ってしまう、…のように1つの箱にその数字が入ってしまう場合の数は、3!×4=24通り。次に、1と2の箱に1と2の数字がそれぞれ入ってしまう場合のように、2つの箱にその数字が入ってしまう場合は、どの箱が重複するかは\(\small {}_4 \mathrm{C}_2 \)通りで、残りの2つの箱に入れる数字は適当でいいので2!通りなので、\(\small {}_4 \mathrm{C}_2 \times 2!=12\)通り。同様に3つの箱にその数字が入る場合の数は、\(\small {}_4 \mathrm{C}_3 \times 1!=4\)通り、すべての箱にその数字が入る場合の数は1通りとなります。なので、②の場合の数は、24-12+4-1=15通りです。
よって、今回求める場合の数である③は①-②=24-15=9通りと求めることができます。
箱と数字の個数が少ないうちは樹形図を描いて数え上げるほうが確実かつ簡単ですが、箱と数字の数が5個や10個となると樹形図では書ききれなくなってくるのでこのような計算が必要となってくるので、参考として知っておきましょう。
4.まとめ
今回は、順列計算の問題の解き方として「人を一列に並べる(隣接させる/させない)」、「数字を並べる」問題に関する場合の数の計算方法について解説しました。
順列の問題にはいろいろなパターンがありますが、どんな問題にも共通する考え方としては、「区別するかしないかを意識してものに名前を付ける」、「順列計算が使えそうか判断」、「条件に対して箱を作って並べる(順列計算の基礎知識を活用)」の3STEPで解くことができるということを説明しました。
順列計算をするうえで大事な考え方が詰まった記事になっていると思うので、ここで紹介した考え方は何度も反復してしっかり自分のものにしていきましょう!
では、今回はここまでです。お疲れさまでした!




コメント