数学を勉強しているとふと「今勉強してる数学って、将来何に役立つんだろう?」、「日常生活をするうえで数学って必要なのかな?」という疑問を抱いたことはありませんか?
確かに、数学は他の科目と比べて数学はどんな場面で利用されているのかが分かりにくい側面があり、例えば、国語なら…
・漢字は文字を読むために必要
・読解力が上がれば素早く必要な情報を収集できる など
勉強することによるメリットがイメージしやすいですが、数学はちょっと小難しいこともあり、うやむやにされがちです。
本記事では、そんな疑問を持つ皆さん向けに、数学が役立つ場面と数学を勉強することで得られるメリットについて、私のこれまでの経験をもとに、独断と偏見で解説していきます!
せっかく勉強するのであれば、将来役立たないと思って勉強するよりも、何に役立つのかを知っている方がモチベーションが上がると思うので、どんな場面で数学が利用されているのか一緒に見ていきましょう!
- 数学が身の回りの生活でどのように使われているのか知りたい人
- 数学を勉強することで人生にどのようなメリットがあるのか知りたい人
- 数学を勉強するモチベーションを高めたい人
本記事の要点
今回は、数学が役立つ場面と勉強すべき理由(メリット)について解説していきますが、まずはじめに本記事の結論をお伝えします。
☆重要Point☆
・数学は日常生活のあらゆる場面で利用されている!
・数学力は普段の日常をちょっと良くする
・数学は勉強の仕方によっては、単なる数学力だけでなく、
人生に役立つスキルも鍛えることができる!
では、上記の結論をもとに、具体的な内容について一緒に確認していきましょう!
【超重要】数学が役立つ場面
数学と一口に言っても分野が広いので、レベル別に分けて考えていきます。
たとえば、四則演算(足し算、引き算、かけ算、割り算)や面積の考え方、平均値の意味といった小学生で学習するレベルの数学力(いわゆる算数)は、絶対に知っておくべき必修知識という点は多くの人が納得できるかと思います。
一方で、高校数学で学ぶような2次関数や微分積分などは、日常生活で出てくる概念ではないので、勉強しても意味ないのでは?と感じてしまうのではないでしょうか?
ということで、多くの人が数学って役に立つのか?と疑問に思うときには、大体が中学・高校レベルの難しい数学のことを指していることが多いと思いますので、中学・高校レベルの数学を中心にどんな場面で役立っているのかについて、解説していきます!
算数と数学の利用場面の違い
日常生活で使う機会が多いのが小学生で習う算数であるとすれば、中高で習う数学は日常生活を裏で支えているものだと言えます。
算数であれば、買い物で700円の30%引きがいくらか計算するとき、割合という数学の知識をそのまま利用しているのでイメージが湧きやすいです。
一方、中高レベルの数学は、日常生活でそのまま利用されることはほぼありません(生活してて2次関数とか出てこない…)。でも、私たちが普段使っているスマホやゲームといった電子機器の仕組みや自然現象を説明したり予測するために用いられる物理法則といった案外身近な場面に応用されています(この後詳しく解説します)。
スマホに数学が使われていると言われても、普通はイメージが湧きません。それは数学をそのまま使っているわけではないからです。中高レベルの数学は、知識と技術を組み合わせることで日常生活に活用できます。そのため、技術のことを学校で習わない中高生が、2次関数って意味ないよねと思ってしまうのは、ある意味当然でしょう。
では、次章以降で数学の知識と技術が組み合わさることでどんなことに数学が利用されているのか一緒に確認していきましょう。利用されている場面は挙げるときりがないので、ここでは3つほど紹介します。
【活用シーン①】整数の性質×情報処理
整数の性質で学ぶ2進数の知識を、画像や映像を表示させるような情報処理技術に応用した例を見ていきます。
パソコンやスマホ、ゲームといった電子機器では、画面にいろいろな情報(文字、動画など)を表示していますが、実はその裏側では様々なプログラムが動いて情報処理をしています。
普段何気なく使っているスマホの画面に表示される画像や映像は、実は0 or 1の情報の羅列(2進数)によって構成されており、2進数による膨大な情報を瞬時に処理することで画面に映し出す情報を制御する仕組みになっています。
これだけだと2進数で画面の情報を映しだしてるってどういうことだかイメージが湧かないと思うので、例として画面に色を表示する仕組みを紹介します。
スマホなどの電子機器で色を表現する際には、すべての色に対して2進数を割り当てています。割り当て方は、全ての色は、赤、緑、青の3色の割合によって表現できることを利用して、赤色ゾーン+緑色ゾーン+青色ゾーンの3つのゾーンごとに、その色の割合が100%なら「\(\small 11111111_{(2)}\)」、0%なら「\(\small 00000000_{(2)}\)」という具合に数字を割り当てます(50%なら「\(\small 00001111_{(2)}\)」)。
このような仕組みで0と1の情報を割り当てると、例えば、赤色であれば、「赤:100%、緑、青:0%」なので、「11111111 00000000 00000000\(\small _{(2)}\)」となります。
これだと、プログラムにとっては処理しやすい形なのですが、人間が見ると分かりにくいので、通常は、16進数に変換した「FF0000\(\small _{(16)}\)」という6桁で表記します。これをカラーコードといいます。
このようにすることで、「色を混ぜる」という作業は、スマホ上ではカラーコードの足し算になります。
「赤色と青色を混ぜると紫になる」という法則は、数学的には、
$$\small \color{#FF0000}{1111 0000 0000}_{(2)}+\color{#0000FF}{0000 0000 1111}_{(2)}=\color{#FF00FF}{1111 0000 1111}_{(2)}$$
というようになるわけです。
ここでは色を例に挙げましたが、他のこともすべて0と1の情報に置き換えて管理されており、裏では数学的な計算が利用されています。
【活用シーン②】数学全般×物理
日常で目にする自然現象のほとんどは、物理法則によって説明することができます。そして、物理法則は数式で記述されているので、数学が応用されているわけです。
たとえば、ボールを放物線を描くように投げたときに、どのくらい高くまで到達するかは、
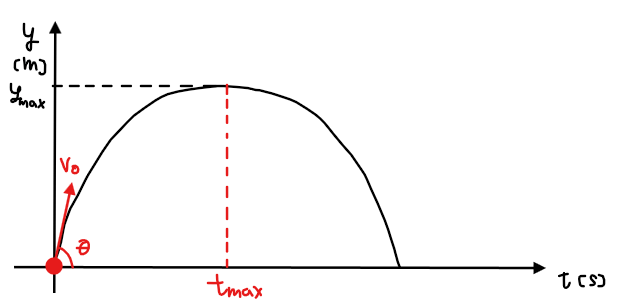
$$\small y=v_0 \sin \theta t-\frac{1}{2}gt^2$$
の公式から計算できます(高校物理の力学で出てきます)。
細かい公式の説明は割愛しますが、\(\small v_0\)がボールを投げる速度、\(\small \sin \theta\)がボールを投げる角度の正弦、\(\small g≒9.8\)なので、例えばボールを投げたときの放物運動が
$$\small y=1.4t-4.9t^2$$
のように表せたとすると、この式は2次関数ですから、最大値は平方完成することで、\(\small y=-0.1\cdot (7t-1)^2+0.1\)より、\(\small t_{max}=1/7≒0.14\)秒後に最大値\(\small y_{max}=0.1\)mに到達することが分かります。
このような計算は日常生活では利用する機会はまずありませんね。では、これが、ロケットを月まで打ち上げするときに、発射台からどのくらいの速度でロケットを飛ばせばよいかを考える場面だったらどうでしょうか?ボールを投げるときのように感覚で打ち上げてしまっては大問題ですよね。
このように、感覚的には分かるけど、より厳密さが求められるような場面(車や家の設計など)では物理法則を通して数学が利用されています。
【利用シーン③】データ分析×金融
データ分析に出てくる正規分布の知識は金融分野で非常によく利用されています。
金融の分野と言われてもあまりピンと来ないかもしれませんが、株価予想をするときに正規分布が使われます(NISAやiDeCoで少しは知っているかな?)。
たとえば、A君がX株に100万円を投資しようとしたとします。X株は平均株価が1000円で標準偏差が300円のおおよそ正規分布に従う値動きをしているとします。このとき、A君の投資する100万円は最悪どの程度まで損するリスクがあるかを計算してみましょう。
データの平均からのずれ具合を表す標準偏差がありますが、平均から標準偏差の2倍以上ずれる確率は5%程度しかないことが計算できます。
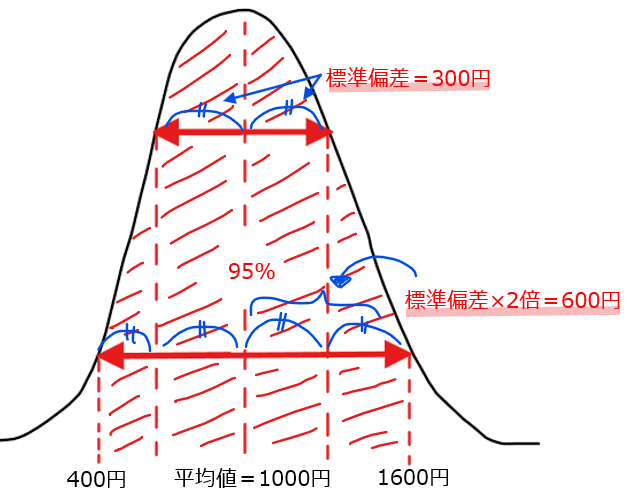
この知識を使うと、標準偏差の2倍が\(\small 300 \times 2 =600\)円なので、X株は平均価格1000円から\(\small \pm 600\)円、すなわち400円~1600円の範囲に値動きが収まる確率が95%だと分かります。
よって、最も損するときの株価の値下がりは95%の確率で-600円になるので、下落幅は\(\small \displaystyle \frac{600}{1000}=60\)%となり、100万円の60%が下落するということで、600万円損する可能性があるということが分かります。
ここで紹介した数字はあくまで例なので、実際は正規分布に従わなかったりと完全に再現できるわけではありませんが、参考情報としてこのような計算をすることができれば、投資の損をしっかりと理解したうえで判断ができるでしょう。
このように、数学を知っていると感覚だけではなく客観的に物事を理解できるため、普段の生活がちょっとお得に感じられます。
【超お得】数学を学ぶべき理由
前章では、数学が利用されている場面について具体例を3つほど紹介しました。
ここまでの話で、中高の数学が日常生活の裏側で大事だってことはなんとなくわかったけど、僕(私)は将来発明家になるわけじゃないから、やっぱり必要ないのでは?と思った人もいると思います。
ただ、数学を勉強することで得られるのは数学の知識だけではありません。
ここからは、個人的に数学を学んだことで人生に役立っていると感じているメリットを紹介していきます。
【メリット①】考え抜く力が身につく
控えめに言っても数学は結構大変な科目だと思います。それは、いろいろな公式を暗記するだけでは太刀打ちできなくて、関数やらベクトルやら微分積分といった、抽象的な概念を理解したり、問題パターンごとの解法を見極めたりなどいろいろな力が必要だからです。
ただ、個人的にはこれらに共通して必要な力が考え抜く力だと思っています。概念や公式を理解するために考える、問題をみてどのような道筋を立てれば答えにたどり着くことができるかを考える、間違えた箇所があれば、自分の考えのどの部分がダメだったのかを考えるなど、数学は考えることばかりです。
考え抜く力は社会人になると非常に重要なスキルになります。なぜならば、社会人の世界では「正解のない物事に対して答えを出すことが求められる」からです。「会社の売上を上げるにはどうしたらいいか?」、「お客さんに喜んでもらえるような接客をするには何が大事か?」、「お金持ちになるにはどんなことをすればいいか?」などなど、仕事もプライベートも絶対的な正解はなく、しいて言うならば自分自身の頭でどれだけ考え抜けるかが正解の精度に直結します。そのため、考え抜く力がある人は自分の人生を充実したものにできるわけです。
いきなり正解のない問題を考えるのは大変ですが、中高の数学にはちゃんと答えがあります(当たり前ですが…)。なので、社会人で必須となる考え抜く力を養う練習として、今皆さんが学習している数学を活用することは、結構ありな選択肢だと思います。今日から皆さんも考え抜くことを意識して数学に取り組んでみましょう!
【メリット②】説明がうまくなる
高校数学が中学校までの数学と大きく異なるのは、「論証」がある点です。ただ答えを導くだけではなく、どのように考えてその解答に至ったのかを相手に分かりやすく的確に説明する必要があります。
実は数学で用いられる論証テクニックは、日常生活で人に物事を論理的に説明する場面で非常に有用です。
たとえば、友達に「卒業旅行は京都に行くのがおすすめ!」ということを論理的に説明したい場合を考えてみましょう。ただ何となく京都旅行がいいよーだけだとちょっと納得感に欠けます。
そこで、三段論法を使えば、
・卒業旅行では、観光スポットやグルメが多い場所がおすすめ
・京都は金閣寺や清水寺など観光スポットが多く、
おしゃれなカフェや食べ歩きできるお店も多い
・よって、卒業旅行で京都に行くのがおすすめ
という説明ができます。
●三段論法とは
「\(\small A=B、A=C\)。よって\(\small B=C\)。」を導き出す論法。
\(\small B\)も\(\small C\)も\(\small A\)であることから、両者が同じだという結論を導き出すことができます。
他にも、帰納法を使えば
・A先輩は卒業旅行は京都がおすすめと言っている
・両親も卒業旅行は京都にしてよかったと言っている
・ネットでも卒業旅行の人気No1は京都という記事があった
よって、卒業旅行は京都がおすすめ
という説明ができます。
●帰納法とは
いくつかの事例の共通点から結論を導き出す論法。
数学では、\(\small n=k\)で成り立つ公式が\(\small n=k+1\)でも成り立つことから、すべての\(\small n\)で公式が成り立つことを論証する際に用いられる。
このように、数学の論証で使うテクニックをうまく活用しながら説明することで、説明力が高まります。いろいろな物事を論理的にわかりやすく説明できるようになると、聞いた人の納得感も得られるため、ぜひ見につけたいスキルです。
【メリット③】問題解決力が高まる
世の中には様々な問題がありますね。高校生であれば、テスト範囲が広すぎて勉強が全然終わらない…であったり、社会人であれば、取引先との商談資料を忘れてしまった…などなど。人生は問題の連続といってもよいかもしれません。
では、皆さんは問題に直面したとき、どのような行動をとっていますか?この質問をすると解答パターンは大きく2通りに分かれます。それは、とりあえず面倒だから後回しにする人と、しっかりと問題に向き合って解決しようする人です。
数学の問題はよくパターンゲーと言われますが、問題の本質を見極めて問題をパターン化する力は、問題解決能力を向上させてくれます。「あ、この問題は前にあったあの問題と似てるから、こうやったら解決できそう!」という考え方は、まさに数学の問題を解く思考そのものですね。
問題解決能力はすべての仕事に重要ですし、数学が得意な人は日常生活でも問題が起こったら原因を考えてすぐ対処している人が多いので、生き生きと生活している印象がありますね。
本記事のまとめ
今回は数学がどう役立つのかと勉強するメリットを紹介していきましたがいかがでしたか?
ここまでいろいろなことを述べてきましたが、結局数学って何?という質問に答えるとするならば、様々な分野を支える存在と言えると思います。
数学をモノに例えるならば、水のような存在かなと思っています。
水自体は無色透明の液体でそのままでは味気ないですが、水があることでお米を炊くことができ、水があることで様々な食材が育つことででき、育った食材を使うことでおいしい料理ができます。完成した料理だけを見ても水が使われていることは分かりませんが、水がないとお米も食材も育ちません。
数学も水と同じように、私たちの目に見えないところで日常生活を支える基礎になっているわけです。数学の勉強がつらくなったら、このことを思い出して、数学に感謝しましょう(笑)。
では今回はここまでです。お疲れさまでした!








コメント