今回は、x軸やy軸まわりの回転体の体積の求め方について、分かりやすく解説していきます。また、バームクーヘン型積分と呼ばれるような特徴的な回転体の裏ワザ的な求め方についても紹介します。「回転体の体積ってどうやって考えて解いたらいいの?」、「立式が難しくてよくわからない…」といった悩みを抱えている人向けに、考え方のコツや解き方の流れを丁寧に解説しているのでぜひ最後まで読んでみてください!
- 回転体の体積ってどうやって立式すればいいの?
- 立式後の式変形のわかりやすい解説が欲しい…
- \(\small y\)軸まわりの回転体の問題が苦手…
- 置換積分ってどういうときに使うの?やり方は?
- バームクーヘン型積分ってなに?どういうときに使えるの?
【はじめに】回転体の体積の考え方
回転体の体積を求める公式と言われると真っ先に思いつくのが以下の公式だと思います。
■回転体の体積の求め方
下図のような\(\small y=f(x)\)と\(\small x=a\)、\(\small x=b\)、\(\small x\)軸で囲まれた部分を\(\small x\)軸まわりに回転させた立体の体積\(\small V\)は
$$\color{red}{V=\int_{a}^{b} \pi \{f(x)\}^2 dx}$$

では、この公式の意味を簡単に説明できますか?ここでいう「簡単に」とは証明で示すとかではなく、「感覚的でもよいので自分の言葉でこの公式が回転体の体積になるのはなぜかを説明できるか?」という意味です。
どうでしょう?そもそもこの公式が「\(\small x\)軸まわりの回転体の公式だ」ということを意識できてない人も多いのではないでしょうか?
回転体の問題で立式に悩む人の多くはこの質問に答えられていない人多いです。式の意味が分かっていなければ、回転軸が\(\small y\)軸まわりや軸が斜めに変わった途端に立式ができなくなるのも当然ですね。なので、まずは回転体の体積計算の基本である\(\small x\)軸まわりの公式の意味から理解していきましょう!
\(\small x\)軸まわりの回転体の公式の意味
ここからは、私なりに回転体の体積の求め方を簡単に説明していきます。なぜ\(\small x\)軸まわりの回転体の体積が\(\small \color{red}{V=\int_{a}^{b} \pi \{f(x)\}^2 dx}\)で求めるのかを一言でいってしまえば、「円柱の微小体積を積み上げることで求まるから」になります。
■回転体の体積を求める公式の考え方
円柱の微小体積を積み上げれば回転体の体積になる!
どういうことか図を使って解説します。

上図のように回転体を\(\small a\)~\(\small b\)の間の「とある\(\small x\)」で切断すると断面は円形になります(黄色部分)。このときの\(\small y\)座標は\(\small f(x)\)なので、断面である黄色い円の半径は\(\small f(x)\)ということになります。よって、黄色い円の面積は、(半径)×(半径)×\(\small \pi=\{f(x)\}^2\pi\)となります。
ここで下図のように\(\small x\)から微小な幅\(\small dx\)を考える黄色い円を底面、\(\small dx\)を高さとした微小な円柱ができます(下図の薄紫部分)。
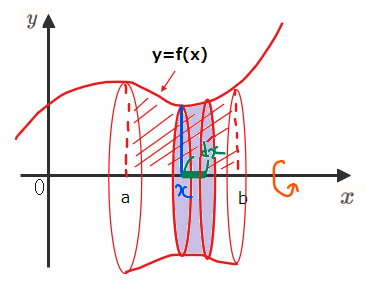
この微小な円柱の体積は、(微小体積)=(底面積)×(高さ)=\(\small \color{red}{\{f(x)\}^2\pi} \times \color{green}{dx}=\color{purple}{\pi \{f(x)\}^2 dx} \cdots①\)。図ではわかりやすいように\(\small dx\)を分厚めに書きましたが、実際には高さである\(\small dx\)は、ほぼ0に近い微小な高さになります。
この微小体積を\(\small x=a\)~\(\small x=b\)まで積み上げていったものが求める回転体の高さになるので、①を\(\small a\)~\(\small b\)まで積分で積み上げることで、\(\small \color{red}{V=\int_{a}^{b}(微小体積)=\int_{a}^{b} \pi \{f(x)\}^2 dx}\)という公式にたどり着きます。
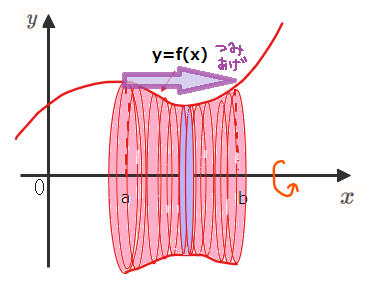
積み上げたものが回転体の体積\(\small x=V\)になる
これが冒頭の微小体積である円柱を積み上げるという意味になります。

体積計算の基礎は「微小体積の積み上げ」
\(\small x\)軸まわりの回転体の体積の公式説明で解説した「円柱の微小体積を積み上げれば回転体の体積になる」という考え方は\(\small x\)軸まわりの回転体でなくてもあてはまる一般的な考え方です。このあとにでてくる\(\small y\)軸まわりの回転体や本記事では扱いませんが斜軸回転体(斜めになっている軸の周りの回転体)の体積なども「円柱の微小体積を積み上げる」という考え方で立式ができます。
さらに、もう少し一般的には「微小体積を積み上げれる」ことで体積を求めることができます。無理やりイメージを数式化するなら、
$$V=\int_{\textrm{範囲}} S(x) dx\quad \cdots (*)$$
となります。\(\small S(x)\)が断面積で、\(\small S(x)dx\)が微小体積になります。これを「ある範囲(下図であれば青色の物体A内部)」で積み上げることで体積になるという式です。
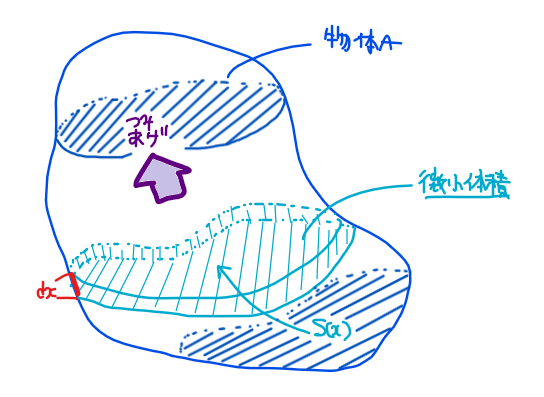
回転体の場合は、断面積が必ず円になるので\(\small S(x)=\pi \{R(x)\}^2\)という形になります(\(\small x\)軸まわりの回転体であれば半径\(\small R(x)=f(x)\)ということ)。
式\(\small (*)\)は、回転体に限らず一般的にどんな形の体積であっても微小体積が分かればそれを積分で積み上げることで体積が計算ができるといっています。今回の記事では詳しくは解説しませんが、難関大学の入試問題などででてくる「非回転体の体積積分の問題」ではこの考え方が大事になるので頭の片隅に入れておくとよいでしょう。
【解き方解説】回転体の問題を解くコツ
一般的に知られている回転体の体積を求める公式、\(\small \color{red}{V=\int_{a}^{b} \pi \{f(x)\}^2 dx}\)は\(\small x\)軸を軸として回した場合のみ使える公式だということを説明しました。
ただ、実際には\(\small y\)軸や直線\(\small y=x\)まわりの回転など\(\small x\)軸まわりの回転ではない問題もあるわけなので、「\(\small x\)軸まわりの回転じゃないときにはどうやって解けばいいの?」と疑問に思った人も多いと思います。
結論、しっかりとした公式ではありませんが、回転体の体積を求める公式は以下のようなイメージを持っておきましょう。
■回転体の体積を求める公式
回転軸からの距離(半径)を\(\small R(t)\)、回転軸を\(\small t\)軸とし、\(\small t=a\)から\(\small t=b\)まで積み上げるとき、回転体の体積\(\small V\)は
$$V=\int_{a}^b \pi \{R(t)\}^2 dt$$
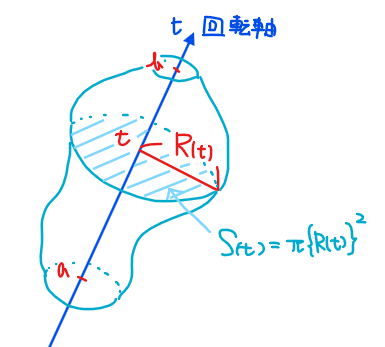
■立式の手順
①回転軸を確認する
②回転軸を積分変数として(上記なら \(\small t\))、始点と終点を積分範囲とする
③断面の半径を積分変数 \(\small t\)の関数 \(\small R(t)\)として表す
\(\small \pi \{R(t)\}^2\)の形はさっきの微小体積の断面積の説明をするときに出てきましたね。
これだけ見ると、「\(\small f(x)\)が\(\small R(t)\)になって、\(\small x\)が\(\small t\)になっただけ?」、「それならこんな公式覚える意味ないんじゃない?」と思った人もいるかもしれません。
公式自体は\(\small x\)軸まわりの場合とほぼ同じですが、一度騙された気分で覚えてみてください。きっとこのあとの回転体を求める問題で役立つと思います。
また、立式の手順もまだイメージはわかないと思いますので、このあとの問題を解く中で詳しく解説してきます!
【問題&解説】回転体の体積計算
【問題1】\(\small x\)軸まわりの回転体の体積
\(\small y=-x^2+x\)と\(\small x\)軸で囲まれた領域を\(\small x\)軸まわりに一回転させた回転体の体積を求めよ。
問題の領域を図示すると下図の斜線部分になります。

これを\(\small x\)軸まわりに回転させるということは、下図のような立体になり、黄色で示した断面積を\(\small x=0\)~\(\small x=1\)まで積み上げればよいわけです。
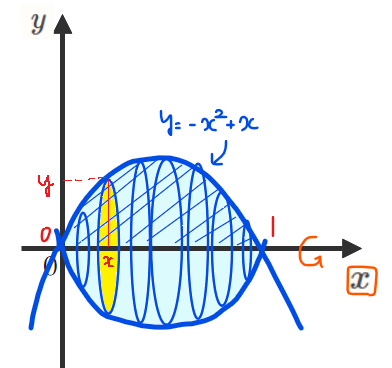
黄色い断面積の半径は\(\small y\)、つまり\(\small -x^2+x\)なので、断面積は\(\small \pi(-x^2+x)^2\)となります。これを積み上げていけばよいので、求める回転体の体積は
$$V=\int_{0}^1 \pi(-x^2+x)^2 dx$$
で求められます。あとはこの積分を計算すると
\begin{equation}
\begin{split}
\int_{0}^1 \pi(-x^2+x)^2 dx&=\pi\int_{0}^1 (x^4-2x^3+x^2) dx\\
&=\pi\left[\frac{x^5}{5}-\frac{x^4}{2}+\frac{x^3}{3} \right]_{0}^1\\
&=\pi\left(\frac{1}{5}-\frac{1}{2}+\frac{1}{3} \right)\\
&=\color{red}{\frac{\pi}{30} \cdots(答)}\\
\end{split}
\end{equation}
(解答)
\(\small \displaystyle \quad \color{red}{\frac{\pi}{30}}\)
【問題2】\(\small y\)軸まわりの回転体の体積
\(\small y=\log(x+2)\)と\(\small x\)軸と\(\small y\)軸で囲まれた領域を\(\small y\)軸まわりに一回転させた回転体の体積を求めよ。
問題文の領域を図示すると以下の青線部分ようになります。
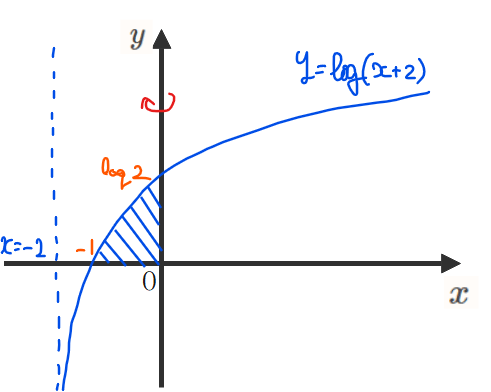
ここで、回転体の体積\(\small V\)を
$$V=\int_{-1}^0 \pi \{\log(x+2)\}^2 dx$$
と立式してしまった人は要注意です。これだと青色部分を\(\small x\)軸まわりに回転させた場合の体積になってしまいます…。今回は\(\small y\)軸まわりなので前章で述べた立式手順に沿って考えてみましょう。
■立式の手順 (再掲)
①回転軸を確認する
②回転軸を積分変数として(上記なら \(\small t\))、始点と終点を積分範囲とする
③断面の半径を積分変数 \(\small t\)の関数 \(\small R(t)\)として表す
①の回転軸は\(\small y\)軸なので、②から考えます。
回転軸は\(\small y\)軸なので、積分変数を\(\small y\)として積分範囲を決定します。すると、今回の回転体では\(\small y=0\)を始点として\(\small y=\log 2\)までが積分範囲になるので
$$V=\int_{0}^{\log 2}\boxed{\vphantom{0}\qquad} dy \quad \cdots (*)$$
の部分まで立式ができます。
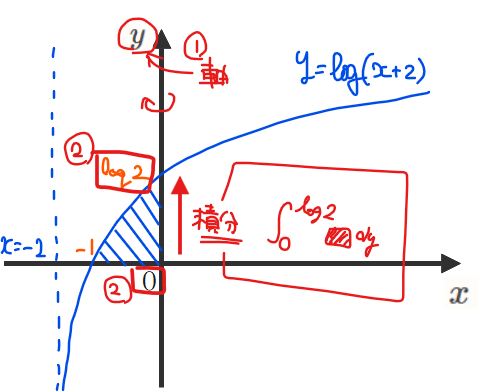
最後に中身の四角部分が決まればよく、それが③に書いた「半径を積分定数(今回だと\(\small y\))の関数として表す」です。
今回の回転体では半径は下図の緑線部分になります。③の手順ではこの長さを\(\small y\)の関数として表せと言っているわけです。

一見すると難しそうですが、緑線の長さは\(\small x\)座標の絶対値なので、\(\small y=\log(x+2)\)を\(\small x\)について解いてあげればよく、
\begin{equation}
\begin{split}
&y=\log(x+2)\\
&x+2=e^y\\
&x=e^y-2\\
\end{split}
\end{equation}
よって半径を表す関数は\(\small |x|=|e^y-2|=2-e^y\)(上図より青線の範囲では常に\(\small x\)座標は負のため)なので、回転体の断面積は \(\small \pi(2-e^y)^2\)。

以上より、\(\small (*)\)は
\begin{equation}
\begin{split}
V&=\int_{0}^{\log 2}\pi(2-e^y)^2 dy\\
&=\pi \int_{0}^{\log 2}(4-4e^y+e^{2y}) dy\\
&=\pi \left[4y-4e^y+\frac{e^{2y}}{2}\right]_{0}^{\log 2}\\
&=\pi \left[ \left(4\color{red}{\log 2} -4e^{\color{red}{\log 2}}+\frac{e^{2\color{red}{\log 2}}}{2}\right)-\left(4\cdot \color{blue}{0} -4e^{\color{blue}{0}}+\frac{e^{2\cdot \color{blue}{0}}}{2}\right) \right]\\
&=\pi \left[ \left(4 \log 2 -4\cdot \color{red}{2}+\frac{\color{red}{4}}{2}\right)-\left( -4\cdot\color{blue}{1}+\frac{\color{blue}{1}}{2}\right) \right]\\
&=\pi \left(4 \log 2 -\frac{5}{2} \right)\\
&=\color{red}{\frac{1}{2}\pi \left(8 \log 2 -5 \right)\cdots(答)}\\
\end{split}
\end{equation}
(補足)\(\small e^{\log a}\)の計算
途中式で、\(\small \color{red}{e^{\log a}=a}\)の関係を使っています。これは両辺の\(\small \log\)をとると、
\begin{equation}
\begin{split}
\log e^{\log a}&=\log a\\
(\log a)\log e&=\log a\\
\log a&=\log a\quad (∵ \log e =1)\\
\end{split}
\end{equation}
となり、左辺=右辺となることから等式が正しいことは分かります。そもそも、\(\small \log a\)とは自然対数\(\small e\)を\(\small \log a\)乗したら\(\small a\)になる数という定義なので、定義からも\(\small a\)になることが分かります。
途中式変形memo
\(\small e^{2 \log 2}=e^{\log 2^2}=e^{\log 4}=4\)
(解答)
\(\small \displaystyle \quad \color{red}{\frac{1}{2}\pi \left(8 \log 2 -5 \right)}\)
【問題3】\(\small y\)軸まわりの回転体の体積(置換積分の利用)
\(\small y=\cos x\)(\(\small 0≦x≦\pi\))と\(\small y=-1\)、\(\small y\)軸で囲まれた部分を\(\small y\)軸まわりに回転させてできる立体の体積を求めよ。
問題文の領域を図示すると下図の赤線部分になります。

図から、回転軸の\(\small y\)軸に沿って、\(\small -1≦y≦1\)まで積分すればよいので求める体積を\(\small V\)とすれば
$$V=\int_{-1}^{1} \boxed{\vphantom{0}\qquad} dy \quad \cdots (*)$$
という形で計算できるというところまでは分かります。あとは四角部分を「③断面の半径を積分変数 \(\small y\)の関数 \(\small R(y)\)として表す」の要領で埋めていけばよいわけです。
回転体の半径は、\(\small y\)軸と\(\small y=\cos x\)の間の距離(下図の緑線)なので、この長さを\(\small x_1\)とおけば、回転体の断面積は \(\small \color{green}{\pi (x_1)^2\cdots(a)}\)と表せます。あとは、\(\small x_1\)を積分変数である\(\small y\)の関数で表すことができればokとなります。

緑線の長さは\(\small y=\cos x\)の\(\small x\)座標の値なので、結局、問題2のように「\(\small x=\cdots\)」の形になるように\(\small x\)について解いてあげればよいのです。
…が、ここで問題にぶち当たります。問題2では\(\small \log\)の関数だったので、指数関数を使うことで「\(\small x=\cdots\)」の形にすることができました。しかし、今回の三角関数は\(\small y=\cos x\)を「\(\small x=\cdots\)」の形にすることができません。
このような場合は、半径の関数を「\(\small x=\cdots\)」の形にすることはあきらめ、その代わりに、積分変数の方を\(\small y\)から\(\small x\)に変換するという置換積分を利用することで解くことができます。
■置換積分の使い道
置換積分は半径を回転軸の関数で表すことができないときに使うべし!
<置換積分の手順>
①回転軸を積分変数として一旦立式する
②置換積分で積分変数を変換する
└積分範囲の変換
└微小変化量の変換
置換積分の手順に従ってこの問題を解いてみましょう。①は式\(\small (*)\)のことで立式済なので②からいきます。
まずは積分範囲の変換をします。現状、\(\small -1≦y≦1\)の範囲になっているので、これを\(\small x\)の範囲に直してあげましょう。値の求め方は\(\small y=\cos x\)の\(\small y\)の値に-1と1をそれぞれ代入して\(\small x\)の値を求めてもよいですが、冒頭に図を描いているので、図を見れば\(\small x\)の値が一目瞭然です。

よって、積分範囲は\(\small \color{red}{\pi ~0\cdots (b)}\)になります(順番に気を付けます)。
次に、微小変化量の変換をします。「微小変化量ってなに?」と思ったかもしれないですが、積分の最後についている\(\small dy\)とか\(\small dx\)ってやつのことです。今回は、\(\small y\)の積分なので\(\small dy\)となっているのを\(\small x\)の積分に変換したいので、\(\small dx\)の形に直してあげる必要があります。
直し方は簡単で、\(\small y=\cos x\)の両辺を微分することで、\(\small \color{red}{dy = -\sin x dx \cdots(c)}\)となります。
変換の準備は以上なので、あとは\(\small (a)、(b)、(c)\)を\(\small (*)\)に代入してあげれば
\begin{equation}
\begin{split}
V&=\int_{-1}^{1} \pi (\color{green}{x_1})^2 dy\\
&=\int_{\color{red}{\pi}}^{\color{red}0} \pi x^2 \color{red}{(-\sin x)dx}\\
&=\pi \int_{0}^{\pi} x^2 \sin x dx\\
\end{split}
\end{equation}
(補足)途中式の変形について
1行目から2行目の式変形で\(\small x_1\)が\(\small x\)に代わっていますが、これは、\(\small x_1\)はもともと「\(\small y\)軸と\(\small y=\cos x\)の間の距離」としていたので、つまりは\(\small x\)座標のことです。なので、\(\small x_1=x\)としています。
上式を部分積分で解くと答えになります。
\begin{equation}
\begin{split}
V&=\pi \int_{0}^{\pi} x^2 \sin x dx\\
&=\pi \bigg[\color{red}- x^2 \color{red}{\cos x}\bigg]_{0}^{\pi} +\pi \int_{0}^{\pi} \color{blue}{2x} \cos x dx\\
&=\pi \times \pi^2 +2 \pi\bigg[ x \color{red}{\sin x} \bigg]_{0}^{\pi} -2 \pi \int_{0}^{\pi} \color{blue}{1} \sin x dx\\
&=\pi^3+0 -2 \pi \bigg[ \color{blue}{-\cos x} \bigg]_{0}^{\pi}\\
&=\pi^3-2 \pi \left( 1+1\right)\\
&=\color{red}{\pi^3-4 \pi \quad \cdots (答)}\\
\end{split}
\end{equation}
(解答)
\(\small \pi^3-4 \pi\)
【問題4】\(\small y\)軸まわりの回転体の体積(バームクーヘン型積分)
\(\small y=\sin x\)(\(\small 0≦x≦\pi\))と\(\small x\)軸で囲まれた部分を\(\small y\)軸まわりに回転させてできる立体の体積を求めよ。
■バームクーヘン型積分を使うタイミング
回転軸と領域が離れていたら『バームクーヘン』
→全体部分から空洞部分を引き算で求めよ!
徹底解説①:回転体の半径は?
\(\small y=\sin x\)(\(\small 0≦x≦\pi\))と\(\small x\)軸で囲まれた部分は下図の青線部分になります。
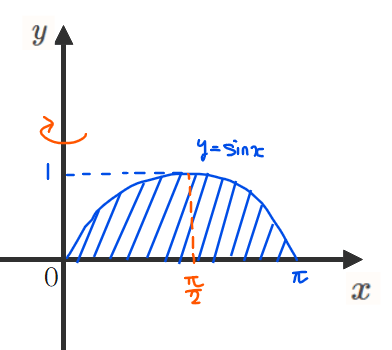
この問題も問題2と同様の3stepで解いてみます。
回転軸は\(\small y\)軸(step①)、積分範囲は、\(\small y=0\)から\(\small y=1\)の区間(step②)であり
$$V=\int_{0}^{1}\boxed{\vphantom{0}\qquad} dy$$
最後はstep③の「断面の半径を積分変数 \(\small y\)の関数 \(\small R(y)\)として表す」です。
では皆さん、突然ですがクイズです。今回の回転体の半径はどこでしょう?
Question:回転体の半径は?
① \(\small y=\sin x\)と\(\small x\)軸との間
② \(\small y=\sin x\)の右端から左端の間
③ \(\small y\)軸と\(\small y=\sin x\)の右端との間
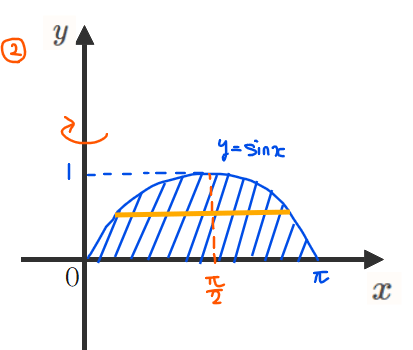

実は①~③はどれも不正解です。でも、半径をこれらの3パターンのどれかだと思って間違えてしまう人が多いのであえてクイズ形式にしてみました。なので、「あれ?①~③のどれも半径じゃないぞ!?」と気づけた人はかなり理解度が高まっていると思います。
徹底解説②:回転体の断面の形
少し本題からそれますが、なぜ①~③が回転体の半径ではないのかという理由について解説します。立式するうえでとても重要な考え方になるのでしっかり理解しちゃいましょう。
今考えているのはstep③にも書いている通り、「回転体の断面の半径」です。半径を考えるためには回転体の断面の形を把握することが重要なので、まずは回転体の断面を考えてみます。

回転させると断面は上図の黄色で示したように真ん中に穴が開いた図形になります。なので、これまでと違ってそもそも断面の形が円ではないんです!なので、半径なんてものはありません。
(補足)回転体の断面の形がイメージできません。
断面の形を把握するコツとかってありますか?
(解答)断面の形が分かりにくい場合は、次の手順で考えるとわかりやすいです。
●STEP1:回転させる領域を適当なところでカットする
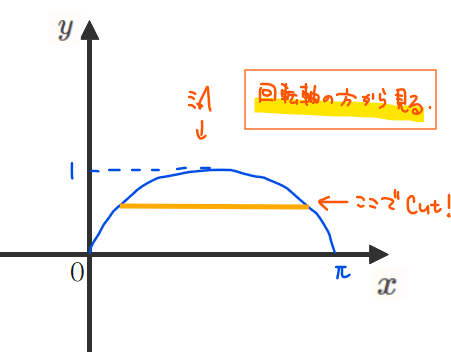
●STEP2:カットした部分を回転軸の方向から眺めた図を描く

●STEP3:STEP2の図形を回転させたものが断面の形になる

徹底解説③:バームクーヘン型の体積を求める方法
このように真ん中に空洞が空いた断面の回転体の体積を求める問題は「バームクーヘン型」などと呼ばれています。バームクーヘン型の体積は、全体の体積から空洞部分の体積を引き算することで求めることができます。

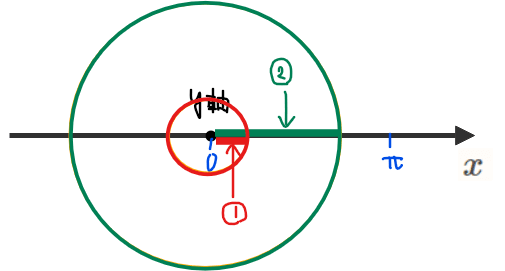
つまり、上図の緑の回転体から赤の回転体を引き算することで求める回転体の体積を計算することができます。立式するのであれば、緑の回転体の半径を\(\small \color{green}{x_2}\)、赤の回転体の半径を\(\small \color{red}{x_1}\)とおけば
$$V=\int_{0}^{1} \color{green}{\pi(x_2)}^2 dy-\int_{0}^{1} \color{red}{\pi(x_1)}^2 dy \quad \cdots (*)$$
あとは、\(\small x_1、x_2\)を\(\small y\)の式で表して積分計算すればよいのですが、ここでも問題が発生します。それが、「\(\small y=\sin x\)を「\(\small x=\)(\(\small y\) の関数)」の形にできない!!」という問題です。このような場合は、問題3でも出てきましたが、置換積分を利用しましょう。つまり、積分の方を\(\small y\)の積分から\(\small x\)の積分に変換してあげればよいのです。
徹底解説④:積分変数の変換(置換積分)
では、以下の積分変数の変換方法に従って変換していきます。
<置換積分の手順>
①回転軸を積分変数として一旦立式する
②置換積分で積分変数を変換する
└積分範囲の変換
└微小変化量の変換
まずは\(\small (*)\)式の第1項目の積分変数から変換していきます。

\(\small x_2\)は外円の半径、すなわち\(\small y\)軸と\(\small y=\sin x\)の右端(上図緑部分)との距離なので、\(\small y\)の積分範囲と\(\small x\)座標の対応関係は
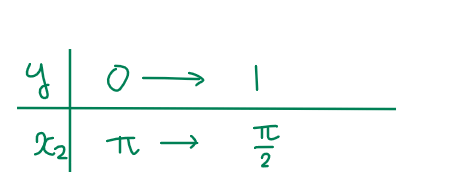
よって、積分範囲は、\(\small \displaystyle \color{red}{ \pi ≦ x_2 ≦ \frac{\pi}{2}\cdots(\mathrm{A})}\)と変換できます。これが「積分範囲の変換」です。
次にもう一つ忘れてはいけないのが、微小変化量、つまり\(\small dy\)を\(\small dx_2\)に変換することです。これは、\(\small y=\sin x_2 \)の両辺を微分することで
$$\color{red}{dy=\cos x_2 dx_2 \quad \cdots (\mathrm{B})}$$
とわかります。
よって、(A)、(B)より、第1項目の積分は
\begin{equation}
\begin{split}
\int_{0}^{1} \pi (x_2)^2 dy &= \color{green}{\int_{\pi}^{\frac{\pi}{2}}} \pi(x_2)^2 \color{green}{\cos x_2 dx_2}\\
&=\int_{\pi}^{\frac{\pi}{2}} \pi x^2 \cos x dx \quad \cdots (1)\\
\end{split}
\end{equation}
(補足)定積分の積分変数は変えても問題ない
最後の式変形で積分変数が\(\small x_2\)から\(\small x\)に置き換わってますが、定積分であれば、積分変数が何であっても最終的に値を代入したら数値になるので、積分変数を勝手に変えても問題ないことを利用しています。\(\small x\)の下に小さく2が付くとごちゃごちゃして見えるのでシンプルに\(\small x\)にしてるのと、少し先走って言うとこのあとでてくる第2項目との合体を目論んでいます。
続いて第2項目の積分変数の変換をします。やり方自体は同じなのでサクッといきますが、

上図から、\(\small x_1\)の積分範囲は\(\small 0≦ x_1 ≦ \frac{\pi}{2}\)、

微小変化量の関係式は、\(\small dy=\cos x_1 dx_1\)なので、
\begin{equation}
\begin{split}
\int_{0}^{1} \pi (x_1)^2 dy &= \color{red}{\int_{0}^{\frac{\pi}{2}}} \pi (x_1)^2 \color{red}{\cos x_1 dx_1}\\
&=\int_{0}^{\frac{\pi}{2}} \pi x^2 \cos x dx \quad \cdots (2)\\
\end{split}
\end{equation}
(1)、(2)の結果より、求める体積の公式\(\small (*)\)は
\begin{equation}
\begin{split}
V&=\int_{0}^{1} \color{green}{\pi (x_2)}^2 dy-\int_{0}^{1} \color{red}{\pi (x_1)}^2 dy\\
&=\int_{\pi}^{\frac{\pi}{2}} \pi x^2 \cos x dx-\int_{0}^{\frac{\pi}{2}} \pi x^2 \cos x dx\\
&=\color{blue}{-\int_{\frac{\pi}{2}}^{\pi}} \pi x^2 \cos x dx-\int_{0}^{\frac{\pi}{2}} \pi x^2 \cos x dx\\
&=-\pi \int_{0}^{\pi} x^2 \cos x dx\\
\end{split}
\end{equation}
(補足)積分範囲の合体
最後の式変形は
$$\int_{a}^{\color{red}k} f(x)dx+\int_{\color{red}k}^b f(x) dx=\int_{a}^b f(x) dx$$
が成り立つことを利用してます。
徹底解説⑤:積分計算
あとは、積分の計算問題なので淡々と計算していきましょう。\(\small x^2\)は2回微分すれば消えるので、部分積分をすることで(積分は赤字、微分は青字にしています)
\begin{equation}
\begin{split}
V&=-\pi \int_{0}^{\pi} x^2 \cos x dx\\
&=-\pi \bigg[ x^2 \color{red}{\sin x} \bigg]_0^{\pi}+\pi \int_{0}^{\pi} \color{blue}{2x} \sin x dx \\
&=0+\pi \bigg[ 2x \cdot \color{red}{(-\cos x)} \bigg]_0^{\pi}+\int_{0}^{\pi} \color{blue}{2} \cos x dx\\
&=\pi \left( 2\pi \right)+2 \bigg[\color{red}{\sin x} \bigg]_0^{\pi}\\
&=\color{red}{2\pi^2 \cdots (答)}\\
\end{split}
\end{equation}
(解答)
\(\small \color{red}{2 \pi^2}\)
【知っトク】バームクーヘン型積分
問題4のような、中が空洞になる回転体の体積を求めるときに、バームクーヘン型積分という公式があります。公式自体は大学入試では解答に書くことはできないのですが、計算が楽になるので、ここでは公式の証明は行わず、考え方を紹介します。
バームクーヘン型積分の公式
■バームクーヘン型積分
関数\(\small y=f(x)\)(\(\small a ≦ x ≦ b\))と\(\small x\)で囲まれた部分を、\(\small y\)軸まわりに回転させた回転体の体積\(\small V\)は、
$$\color{red}{V=\int_{a}^{b} 2\pi x f(x) dx}$$
公式の導出(厳密ではない)
たとえば、下図のように赤斜線の領域を\(\small y\)軸まわりに回転させた回転体を考えてみましょう。すると、この立体は真ん中がタケノコのようにくりぬかれた形になります。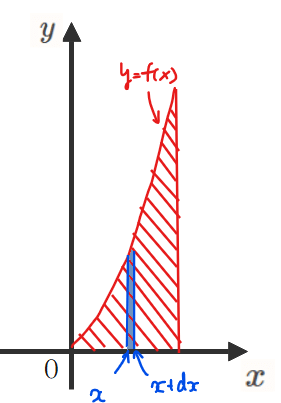
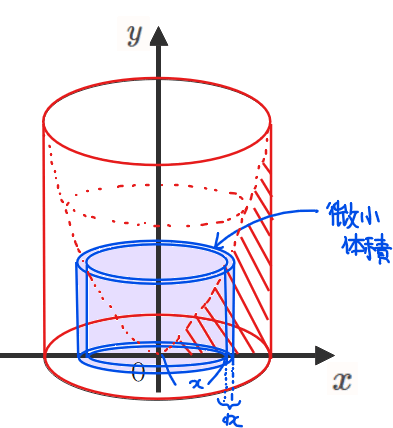
ここで、座標\(\small x\)と\(\small x\)から微小な幅\(\small dx\)だけ離れた部分で囲まれた立体を考えます(上図の青色部分)。\(\small dx\)は非常に小さいので、\(\small \color{red}{(dx)^2=0}\)となること、\(\small \color{red}{f(x)≒f(x+dx)}\)(左上図の\(\small y\)座標は\(\small dx\)が微小であればほとんど同じ)を認めれば、青色の円柱状の立体の体積は、底面の半径が\(\small (x+dx)\)の円柱から半径が\(\small x\)の円柱をくりぬけばいいので
\begin{equation}
\begin{split}
V_{\textrm{青色部分}}&=\pi (x+dx)^2 \times f(x+dx)-\pi x^2 \times f(x)\\
&=\pi (x^2+2 x dx+(dx)^2 )f(x+dx)-\pi x^2 f(x)\\
&≒\pi (x^2+2 x dx+(dx)^2 )\color{red}{f(x)}-\pi x^2 f(x)\\
&≒\pi (x^2+2 x dx+\color{red}0)\color{red}{f(x)}-\pi x^2 f(x)\\
&=\pi x^2f(x)+2 \pi x f(x) dx-\pi x^2 f(x)\\
&=2 \pi x f(x) dx\\
\end{split}
\end{equation}
バームクーヘン型積分の公式では、この微小体積\(\small 2 \pi x f(x) dx\)を\(\small a≦ x ≦ b\)の範囲で積み上げるという公式になっていることが分かります。
【問題4の別解】バームクーヘン型積分を使った解法
公式より、
\begin{equation}
\begin{split}
V&=\int_{0}^{\pi}2 \pi x\sin x dx\\
&=2\pi \bigg[ x\cdot(-\cos x)\bigg]_{0}^{\pi} +\int_{0}^{\pi}1\cdot \cos x dx\\
&=2\pi^2 +\bigg[\sin x\bigg]_{0}^{\pi}\\
&=\color{red}{2\pi^2 \cdots(答)}\\
\end{split}
\end{equation}
このようにかなり簡単に計算することができます。
バームクーヘン型積分は覚えるべきか?
最後に、バームクーヘン型積分の公式は覚えておいた方がよいのかについて、個人的な見解を述べます。
結論、必須じゃないけど覚えられるなら覚えておいても損はないという感じです。理由は、論述として解答用紙で使うことはできないですが、検算やマークシート方式の試験であれば利用することができるからです。
体積積分の問題がある程度解けるようになって余裕が出てきたら覚えるようにしましょう。
本記事のまとめ
今回は、\(\small x\)軸まわりと\(\small y\)軸まわりの回転体の体積の求め方について説明しました。
今回のポイントは以下の通りです。
■回転体の体積を求める公式
回転軸からの距離(半径)を\(\small R(t)\)、回転軸を\(\small t\)軸とし、\(\small t=a\)から\(\small t=b\)まで積み上げるとき、回転体の体積\(\small V\)は
$$V=\int_{a}^b \pi \{R(t)\}^2 dt$$
■立式の手順
①回転軸を確認する
②回転軸を積分変数として(上記なら \(\small t\))、始点と終点を積分範囲とする
③断面の半径を積分変数 \(\small t\)の関数 \(\small R(t)\)として表す
■置換積分の使い道
置換積分は半径を回転軸の関数で表すことができないときに使うべし!
<置換積分の手順>
①回転軸を積分変数として一旦立式する
②置換積分で積分変数を変換する
└積分範囲の変換
└微小変化量の変換
■バームクーヘン型積分を使うタイミング
回転軸と領域が離れていたら『バームクーヘン』
→全体部分から空洞部分を引き算で求めよ!
■断面の形を把握するコツ
●STEP1:回転させる領域を適当なところでカットする
●STEP2:カットした部分を回転軸の方向から眺めた図を描く
●STEP3:STEP2の図形を回転させたものが断面の形になる
特に回転体の立式手順や断面の形を把握するコツは\(\small x\)軸まわりや\(\small y\)軸まわりの回転体の体積だけでなく、直線\(\small y=x\)まわりの回転体や複雑な領域を回転させる回転体の体積計算などで利用できるかなり応用の利く知識になっているので、今回の問題を通してしっかり理解して身に着けてしまいましょう!
では今回はここまでです。お疲れさまでした!








コメント