今回は、グラフを用いた領域における最大値と最小値の求め方とその実用例である線形計画法について解説していきます。「領域のどこで最大最小になるのかの見分け方がわからない…」、「そもそもグラフをかいて最大最小を求める解き方がよくわからない…」、「線形計画法って何?」といった領域における最大最小の問題に関する悩みを一つずつ解決できる記事になっていると思うので、ぜひ最後まで読んでみてください!
- 領域における最大最小ってどんなパターンがあるの?
- グラフのどの部分で最大値、最小値になるの?
- グラフの傾きや切片など、どこに注目すればいいの?
- 線形計画法って何?
- 具体的な問題の解き方が知りたい!
【はじめに】領域における最大最小ってなに?
領域における最大値、最小値を求める問題が今回のテーマですが、そもそも領域における最大最小ってなんなのか?という話を少しだけしておきます。
これまでに出てきた最大値、最小値を求める問題だと2次関数の問題が思い浮かぶと思います。「\(\small \color{red}{0≦x≦2}\)のとき、2次関数 \(\small \color{blue}{y=x^2}\)の最大値、最小値を求めよ。」、こんなやつですね。この問題を少し言い換えるならば、\(\small 0≦x≦2\)という\(\small x\)の範囲の中で、\(\small y=x^2\)という\(\small y\)の値の最大・最小を求めましょう、という問題ですね。
それと比べて、今回のテーマである領域における最大最小は、「\(\small \color{red}{x≧0、y≧0、y≦-x+1}\) のとき、\(\small \color{blue}{2x-y}\) の最大値、最小値を求めよ。」みたいな問題です。この問題も言い換えるならば、\(\small \color{red}{x≧0、y≧0、y≦-x+1}\) という\(\small xy\)平面上の領域の中で、\(\small \color{blue}{2x-y}\) の値の最大値、最小値を求めましょう、という問題なわけです。
こうして比較してみると「範囲」が「領域」になったりという細かい違いはありますが、大枠は同じだということが分かると思います。2次関数の最大、最小を求めるときは、定義域をかいて、グラフをかいてから、最大最小を求めます。なので領域における最大、最小を求めるときも、領域を図示して、グラフをかいてから、最大最小を求めればいいわけです。
【パターン解説】領域における最大最小でよく出る問題パターン
領域における最大最小を求める問題は、「領域の形」と「求める式の形」からパターン分けすることができます。
【領域の形】よく出るパターン3選
領域の形とは、「\(\small \color{red}{x≧0、y≧0、y≦-x+1}\) のとき、\(\small \color{blue}{2x-y}\) の最大値、最小値を求めよ。」という問題であれば、赤色部分の不等式で表される範囲のことです。
問題として出てくる領域の形のほとんどは、直線、円、放物線の3つの組み合わせで成り立っています。
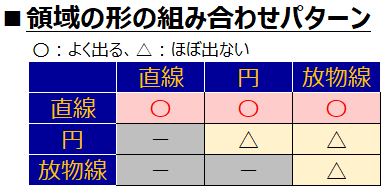
〇がついている箇所が入試などでも頻出の組み合わせで、直線で囲まれた領域における最大最小や、直線と円で囲まれた領域における最大最小などの問題が該当します。
△の箇所は、円や放物線で囲まれた領域になっていて、グラフのどの点で最大・最小となるのかが分かりにくかったり、かなり複雑な式となり計算が困難だったりすることから、入試問題ではほとんど出てきません。
なので、領域の形については基本的には上記の〇がついている3パターンと思っておけばよいでしょう。
【求める式の形】よく出るパターン4選
求める式の形とは、「\(\small \color{red}{x≧0、y≧0、y≦-x+1}\) のとき、\(\small \color{blue}{2x-y}\) の最大値、最小値を求めよ。」という問題であれば、青色部分の式の形のことです。
求める式は、ざっくりと、直線型、円型、放物線型、分数型の4パターンに分かれます。パターン名称は私が勝手につけただけで一般的な呼び方とかではないのでご認識を…
直線型
求める式が、\(\small 2x+y\) のような\(\small x、y\) の一次式(単純な足し算引き算)になっているパターンです。
\(\small k=2x+y\) とおくことで、\(\small y=-2x+k\) のように直線の方程式の形になります。
円型
求める式が、\(\small x^2+y^2\) や\(\small x^2+y^2-4x+2y+1\) のように円の方程式の左辺になっているパターンです。
\(\small k=x^2+y^2-4x+2y+1\) とおくことで、\(\small (x-2)^2+(y+1)^2=k+4\) となり、中心\(\small (2,-1)\)、半径\(\small \sqrt{k+4}\)のように円の方程式の形になります。
放物線型
求める式が、\(\small 4x^2+2y\) のように\(\small x^2\)と\(\small y\)の足し算引き算になっているパターンです。
\(\small k=4x^2+2y\) とおくことで、\(\small \displaystyle y=-2x^2+\frac{k}{2}\)のように放物線の形になります。
分数型
求める式が、\(\small \displaystyle \frac{x+y}{x-2}\) のように\(\small x、y\)の一次式の分数になっているパターンです。分数の形になっていることから分数型と名付けています。
\(\small \displaystyle k=\frac{x+y}{x-2}\) (ただし、\(\small x \neq 2\))とおくことで、\(\small y=(k-1)x-2k\) (\(\small x \neq 2\))のように直線の方程式、つまり直線型にすることができます。
【解き方解説】領域における最大最小の求め方
領域の形3パターンと求める式の形4パターンを解説したところで、ここからは本題の問題の解き方について解説します。いろいろなパターンがありましたが、どんな問題でも解き方の流れは変わりません。
【解き方・考え方の基本】領域における最大最小を求める4ステップ
結論、以下の4ステップで解いていけばokです。
求める式の図形的な意味を確認
求める式を\(\small k\)とおいて、直線型、円型、放物線型、分数型のどれになるかを確認します。また、求める式の形ごとにグラフがどう変わるのかを確認します。
■パターン別:求める式の\(\small k\)の図形的意味
・直線型 :\(\small k\)は切片 →直線が上下に動く
・円型 :\(\small k\)は半径 →円の大きさが変わる
・放物線型:\(\small k\)は切片 →放物線が上下に動く
・分数型 :\(\small k\)は傾き →直線の傾きが変わる
領域を図示
不等式に従って領域を図示します。
最大、最小となる点を特定
STEP1で確認した式の形(直線、円、放物線)とSTEP2で図示した領域の形から、領域のどの点で最大、最小となるかを確認します。
最大最小となる点を見極めるには、問題文の文章を「図形的な問題に言い換える」ことが重要です。
最大値、最小値を求める
STEP3で特定した最大値、最小値となる点を通ることから、\(\small k\)の値(=求める式の値)を計算します。
ちょっとイメージが湧かない部分もあると思うので、ここからは線形計画法の問題を例に実際の解き方を解説していきます。ステップごとに一つずつ理解していきましょう!
【例題で解説】4ステップを使った具体的な解き方
不等式 \(\small x≧0,\space y≧0,\space x+3y≦9,\space 4x+3y≦12\)のすべてを満たす\(\small x, y\)に対して、\(\small x+y\)の最大値、最小値を求めよ。
求める式の図形的な意味を確認
まずは、最大値、最小値を求める式を\(\small \color{red}{k=x+y}\) とおきます。すると、
$$\color{red}{y=-x+k \quad \cdots ①}$$
となるので、直線型です。式①をみると、この直線は傾きが1、切片が\(\small k\)の直線の式なので、直線が\(\small k\)の値によって上下に動くことが分かります。
領域を図示
不等式 \(\small x≧0,\space y≧0,\color{red}{\space x+3y≦9},\space \color{blue}{4x+3y≦12}\)を\(\small xy\)平面上に図示していきます。
たとえば、\(\small \color{red}{x+3y≦9}\) であれば
$$ \color{red}{y≦-\frac{1}{3}x+3\quad \cdots②}$$
よって、②が表す不等式の範囲は、直線 \(\small \displaystyle y=-\frac{1}{3}x+3\) の下側の部分であることがわかります。
補足:線の上側か下側かはどうやって判断する?
そもそも\(\small xy\)平面において、\(\small y\)というのは縦方向の値を表してます。\(\small y\)の値が大きいほど上側で、小さいほど下側です。
これを踏まえると、「\(\small y≦\)式」(式は直線、円、放物線など)という不等式であれば、式の値よりも\(\small y\)の値が小さい=下側ということなので、式(直線、円、放物線)の下側の領域が不等式の表す範囲になるわけです。
不等号が「\(\small y≧\)式」のように逆になっても同じで、\(\small y\)の値の方が大きい=上側の領域ということになります。
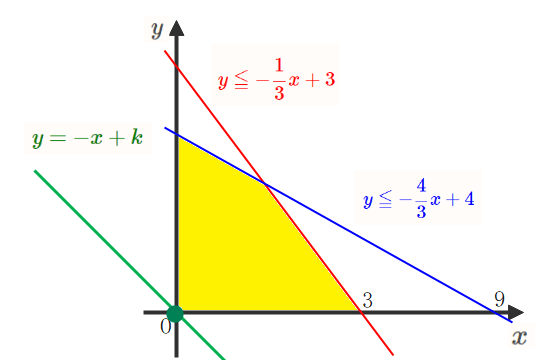
他の不等式も同様に考えると4つの不等式で囲まれる領域は以下の黄色部分(境界を含む)になります。
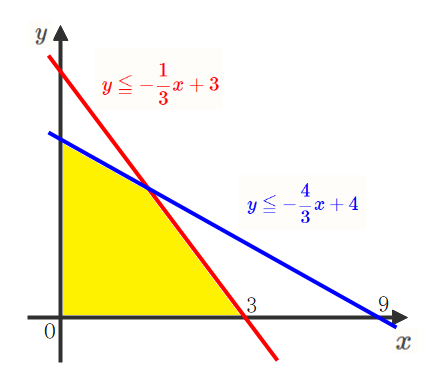
最大、最小となる点を特定
STEP1で確認したように、求める式の形は、傾き1、切片が\(\small k\)の直線です。
今回求める\(\small x+y\)の値を\(\small k\)とおいていたので、\(\small x+y\)の最大最小を求めるということは、切片の最大最小を求めることになります。
なので問題の文章を図形的な問題に置き換えるならば、「黄色い部分を通る傾き1の直線を上下に動かしたときに、切片が一番高くなるところ/一番低くなるところはどこか?」となります。この問題を図形的に考えてあげればよいのです。
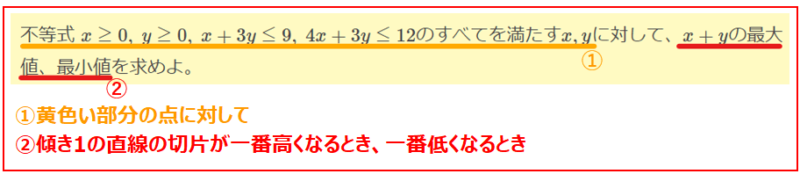
グラフの傾きに注意すると、傾き1の直線(緑線)は、点A\(\small \left(1,\frac{8}{3}\right)\)を通るとき、すなわち\(\small x=1, y=\frac{8}{3}\)のときに切片が最大になることが分かります。
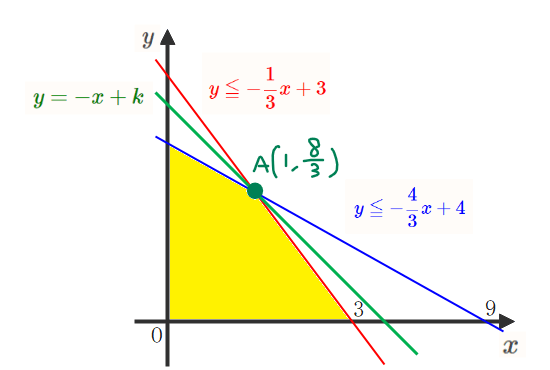
(補足)グラフの傾きに注意!!
グラフをかくときにはそれぞれの直線の傾きに注意します。理由は、傾きの大小が実際と異なる図を描いてしまうと最大や最小となる点を見誤ってしまう可能性があるからです。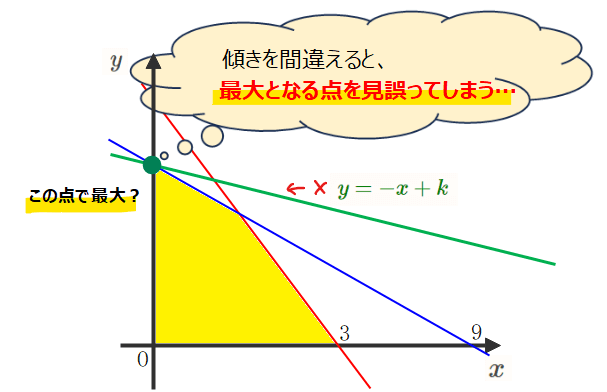
「傾きを正確にって言われてもどこまでちゃんと書けばいいの?」という話ですが、最大最小の問題では、傾きの大小関係が正しければokです。
今回であれば、傾きの大小関係は
$$\textrm{← ゆるやか}\quad \color{blue}{-\frac{4}{3}}<\color{green}{-1}<\color{red}{-\frac{1}{3}} \quad \textrm{急 →}$$
となっている必要があります。
同様に考えると切片が最小となるのは原点を通るとき、すなわち\(\small x=y=0\)のときとなります。
最大値、最小値を求める
最後は、STEP3で特定した最大値、最小値となる点を、\(\small x+y\)に代入すれば答えです。
(解答)
\(\small \displaystyle \color{red}{(x,y)=\left(1,\frac{8}{3}\right)}\)で最大値 \(\small \displaystyle x+y=1+\frac{8}{3}=\color{red}{\frac{11}{3}}\),
\(\small \color{red}{(x,y)=\left(0,0\right)}\)で最小値 \(\small x+y=\color{red}0\).
領域における最大最小の実用例
線形計画法とは?
ここまで領域における最大最小のパターンと解き方について解説してきました。ただ、皆さんの頭の中の片隅には、「正直こんなこと勉強して何の役に立つの?」と疑問に思った人も多いのではないでしょうか?
実は、その答えの一つが、ここで紹介する線形計画法です。
線形計画法とは、ざっくりというならば、経済学などで売上やコストなどを最大化・最小化させるときに用いられる手法です。線形計画法の考え方では、領域における最大最小の考え方が使われており、これまで説明してきたパターンでいうと、領域が直線で囲まれており、求める式の形が直線型のパターンに該当します。
あんな不等式の問題が経済に応用されているの??と思った人もいるかもしれません。具体的にどのように使われているか線形計画法の問題を通して学んでいきましょう。
線形計画法の問題
ある工場では製品A、Bを作っており、単価はそれぞれ、200円、100円である。製品Aを作るためには部品X、Y、Zがそれぞれ1個、2個、3個、製品Bを作るためには部品X、Y、Zがそれぞれ3個、3個、1個必要である。部品X、Y、Zの在庫がそれぞれ180個、210個、210個あるとすると、製品AとBの売上を最大化するためにはそれぞれいくつずつ作って売ればよいか求めよ。
売上を最大化させるために製品Aを\(\small x\)個、製品Bを\(\small y\)個作るとします。
今回求めるのは製品A、Bの売上を最大化することなので、まずは売上を求める式を考えてみます。製品Aの単価が200円なので\(\small x\)個作れば\(\small 200x\)円、製品Bの単価が100円なので\(\small y\)個作れば、\(\small 100y\)円になるので合計の売上は\(\small 200x+100y\)円になります。これが今回求める式の形になります。
なので、\(\small 200x+100y=k\)とおくと、\(\small \displaystyle \color{green}{y=-2x+\frac{k}{100}\cdots①}\)となるので、求める式の形は図形的には傾き-2で上下に動く直線になります。
次に、在庫に関する情報を数式化します。部品Xは180個の在庫がある一方で、製品Aを\(\small x\)個作るためには部品Xを\(\small x\)個、製品Bを\(\small 3y\)個使うので、使用する部品Xは合計で\(\small x+3y\)個であり、この個数が在庫180個以内になるようにしなければいけないという制約があります。これを数式化すると、\(\small \color{red}{x+3y≦180\cdots②}\)となります。
同様に部品Yについても考えると、\(\small \color{red}{2x+3y≦210\cdots③}\)、部品Zについては\(\small \color{red}{3x+y≦210\cdots④}\)が成り立ちます。また、\(\small x, y\)は製品の個数なので、\(\small \color{red}{x≧0, y≧0\cdots⑤}\)も成り立ちます。
以上、②~④を「\(\small y≦\cdots\)」の形に変形すると
\begin{equation}
\begin{split}
&\small y≦-\frac{1}{3}x+60\cdots②\\
&\small y≦-\frac{2}{3}x+70\cdots③\\
&\small y≦-3x+210\cdots④\\
\end{split}
\end{equation}
となので、②~⑤を\(\small xy\)平面上に図式化すると以下の黄色部分(境界を含む)になります。
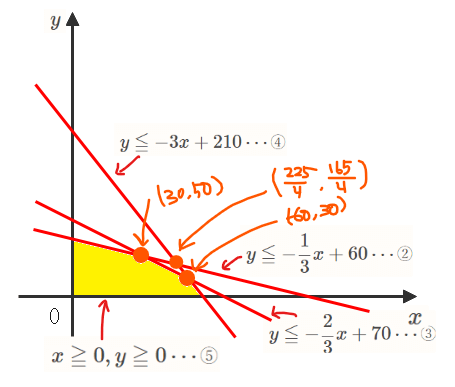
問題を図形的に言い換えると、「黄色部分を通って、傾き-2の直線の切片が最大になるときの\(\small x,y\)座標を求めよ」と言い換えられます。今回の問題では、売上の最大値自体を聞かれているのではなく、あくまで売上が最大となるような製品A、Bの製造個数である点に注意しましょう。
\(\small x, y\)はそれぞれ製品A、Bの製造個数だったので、売上の式①、\(\small \displaystyle \color{green}{y=-2x+\frac{k}{100}}\)の切片が最大となるような座標が黄色部分のどこなのかを求めることが製品A、Bの製造個数を求めることにつながるわけです。
傾きの大小関係に注意して売上の式をグラフ上に書くと、点(60,30)で切片が最大になることが分かります。
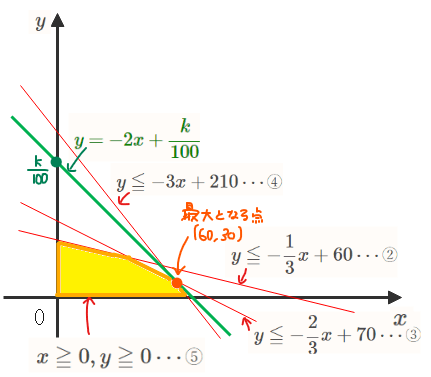
傾きが\(\small -\frac{2}{3}\)の直線③と傾きが-3の直線④の中間の傾きになります。
よって、答えは、売上を最大化するためには製品Aを60個、製品Bを30個作ればよい、となります。
ちなみに、そのときの売上の最大値は、\(\small 200x+100y=200\cdot \color{red}{60}+100\cdot \color{red}{30}=15000\)円になります。
(解答)
製品Aを60個、製品Bを30個ずつ作って売ればよい。
まとめ
今回は、領域における最大最小の求め方とその実用例である線形計画法について解説しました。問題のパターンと解き方をおさらいすると以下の通りです。
■よく出る領域の形3パターンの組み合わせ
■よく出る求める式の形4パターン
・直線型 :\(\small x+y\)などの1次式
・円型 :\(\small x^2+y^2\)など
・放物線型:\(\small x^2-y\)など
・分数型 :\(\small \displaystyle \frac{x+y}{x+2}\)など分数の形になっている
■基本の解き方4ステップ
・STEP1:求める式の図形的な意味を確認
→\(\small k\)とおいて直線型/円型/放物線型/分数型のどれに当てはまるか確認
・STEP2:領域を図示
→不等式の範囲を図示
・STEP3:最大、最小となる点を特定
→図形的な問題に言い換えてみる
・STEP4:最大値、最小値を求める
→\(\small x,y\)の値を代入して\(\small k\)の値を求める
今回の解き方が習得できれば領域における最大最小の基礎はばっちりなので、あとはいろいろなパターンの問題を解く中で経験を積んでいけばどんな問題でも考えて解けるようになります。
問題を解いて実力アップをしたいという人は、「【領域における最大最小】円・直線・放物線で囲まれた領域の最大最小の見分け方」で基本から応用問題まで徹底解説しているのでぜひ解いてみてください!
では本日はここまでです。お疲れさまでした!







コメント