本記事では、正十二面体を4つの色を使って塗分ける方法が何通りあるかについて、解説していきます。もう少し正確に言うと次の問題を解説していきます。
どうやって解くのか少しでも興味がわいた人は、ぜひ最後まで読んでみて下さい!また、本記事で扱う色塗り分け問題については、「領域の色塗分け問題の解法(場合の数)」で基本的な解き方を分かりやすく解説しているので、初めにこちらを確認しておくとよりスムーズに理解ができると思います。
1.【導入編】正十二面体とは
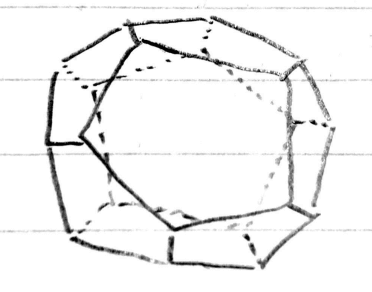
問題に入る前に、まずは今回のメインである正十二面体について簡単に説明しておきましょう。正二十面体は右図のような形をしています。
特徴としては、各面は正五角形になっていて、正面の正五角形を取り囲むように、5個の正五角形があり、それが裏手にもある感じです。ちなみに、正多角形なので、どの面を正面にしても右側の見た目になります。
2.【準備編】正十二面体の展開図と隣接関係図
正十二面体の形と特徴が分かったところで、本題の色の塗分け問題に入っていきましょう。空間の色の塗分けは平面と違って、回転したら同じ塗り方の場合は1通りにカウントされることを考慮する必要があります。前章で述べた正十二面体の特徴の中に、「どの面を正面にしても右の見た目になる」がありました。これは裏を返せば、どんな色の塗り方をしても回転させれば必ず特定の色を上図の正面に持ってくることができるということ。今回はイメージしやすいように、4色の色を、赤、青、黄色、緑の4つとし、正面に必ず赤色が来るようにして正十二面体を見ることにします。
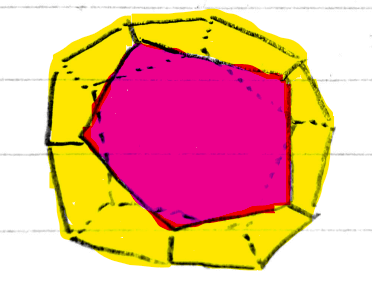
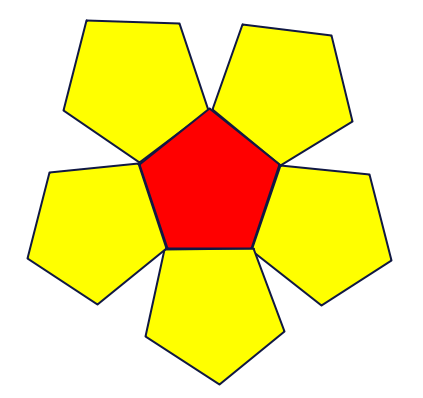
色の塗分けを考えるにあたって立体のまま考えられる人はよいのですが、見えない部分が多くどの面同士が隣り合っているかもぱっと見て分かりにくいので、正十二面体の面同士の隣接関係を平面に落とし込むことを考えます。左下の正十二面体を右下のように展開してあげると、赤い正面の五角形の周りに黄色い五角形が5個くっついた展開図が得られます。
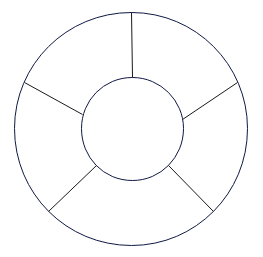
隣接関係だけを図式化するのであれば、簡略的にこんな風に書き表せます(隣接関係図1)。
次に、左下の図の青色の面に注目します。青色の面の周りの面を、紫、赤、黄色、オレンジ、緑と反時計回りに色分けすると展開図は右下のようになります。展開図だと離れているように見えますが、紫、赤、黄色、オレンジ、緑の面は、青色の面と接していることに注意します。
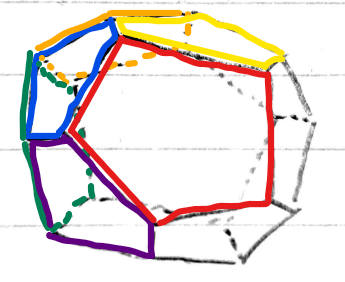
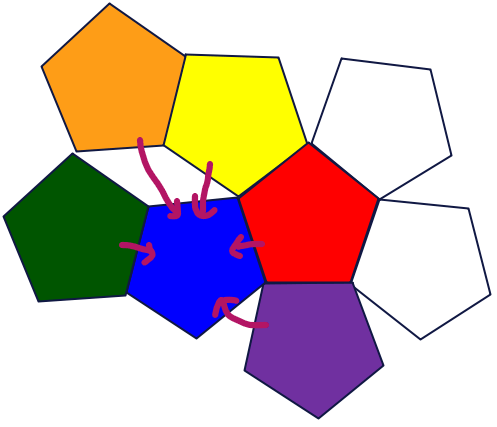
図4の展開図から、図3の青面の裏側の面(オレンジ、緑)との隣接関係を先程描いた隣接関係図1に追加すると、隣接関係図2のようになります。これらの特徴は、図3の赤面の周りの5つの面すべてに共通することなので、他の面に関しても追記すると隣接関係図3になります。

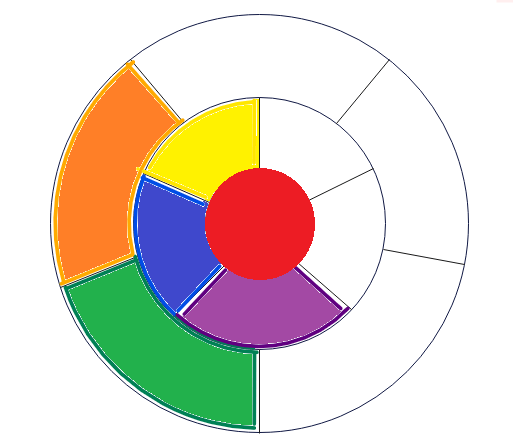
これで11面同士の隣接関係まで図示できて、最後は赤面の裏面との隣接関係です。これは簡単で赤面と同じように周りの5面と隣接しているので(図5の赤、青、緑、紫、オレンジ)、隣接関係図4が正十二面体の各面同士の隣接関係を平面上に図示したものになります(黄色部分が裏面)。
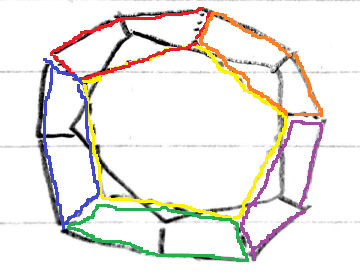
下準備は以上です。各面の隣接関係が分かったので次章からは場合の数を計算していきます。
3.【解答編】塗り分け方法の計算
3.1 領域を塗り分けるときのポイント
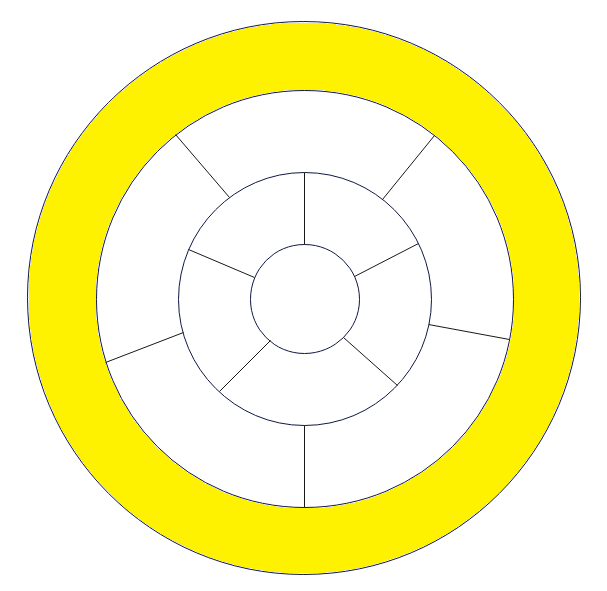
各面との隣接数はどの面も5面で同じなので、今回は内側から外側に向かって色を塗っていきます。面が多いのでローマ数字ではなく、A~Lとアルファベット順に塗っていきます。
Aの面は赤固定と初めに宣言したので、赤です。それ以外の面について、赤、青、黄色、緑の4色で塗り分けていきます。初めはなるべく色がばらけるように塗っていきたいと思います。
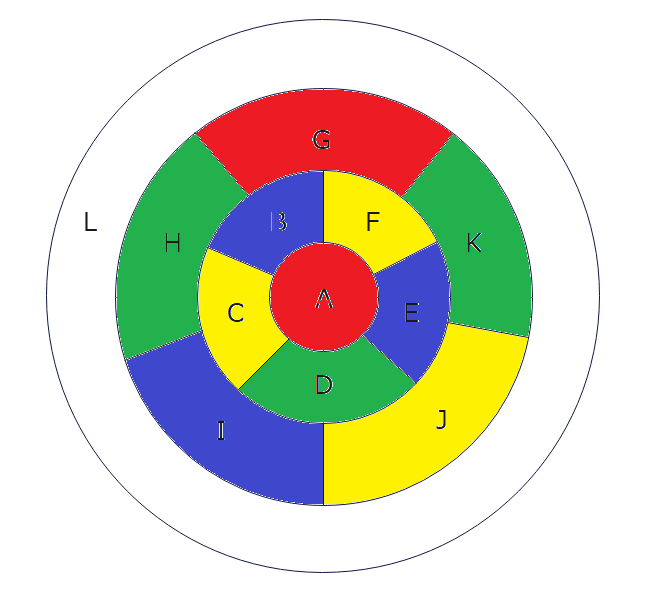
ばらけるように色を塗っていったところ、G~Kに4色すべてが使われていることで、最後のLには塗れる色がない状態になってしまいました。ここで分かった気づきとしては、「LはG~Kと接しているため、G~Kは3色以内で塗らなければいけない」ということです。
3.2 領域の塗り分けパターン
ここからはG~Kを3色以内で塗るパターンを考えていきます。
3色以内といいつつ、実はG~Kは必ず3色で塗る必要があることがすぐにわかります。なぜならば、Gから交互に2色を塗っていくとKとGが同じ色になるため、Kに塗るための3色目が必要になるからです。
もう一つ重要なこととして、B~Fの塗分けパターンは1色+2色が2ペアで2通りのみです(下図参照)。
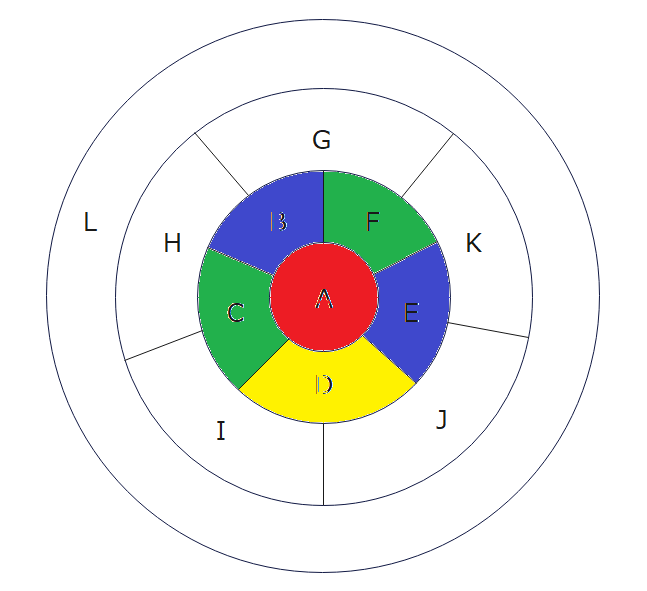
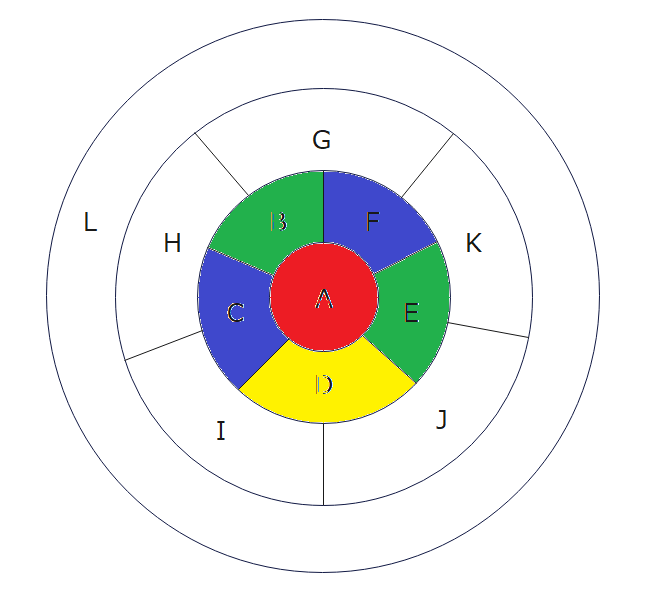
これは実際に塗り分けしてみればすぐにわかりますが、位置関係は立体で回転させることができるので、どう塗っても回転させるとこの塗り分けに帰着します(もちろんどの色で塗るかは別問題)。
最後に、G~Kには必ず赤色が1色は含まれます。これも赤色を使わずに塗分けを頑張ってみるとわかりますが、どうしてもB~Fにない色(=赤色)で塗り分けする必要が出てきます。
よって、G~Kの塗分けは基準点として、G赤色で考えればよく(回転してしまうので)、結果、3色で塗り分けるパターンは以下の2パターンのみになります(Hは緑が確定で、Iは赤or青の2パターン、J、Kは3色しか使えないことを考慮すると以下の2つのみ)。
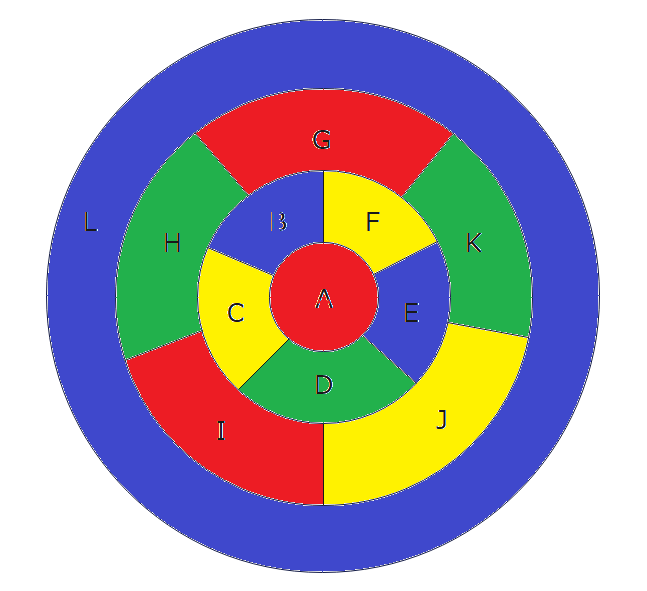
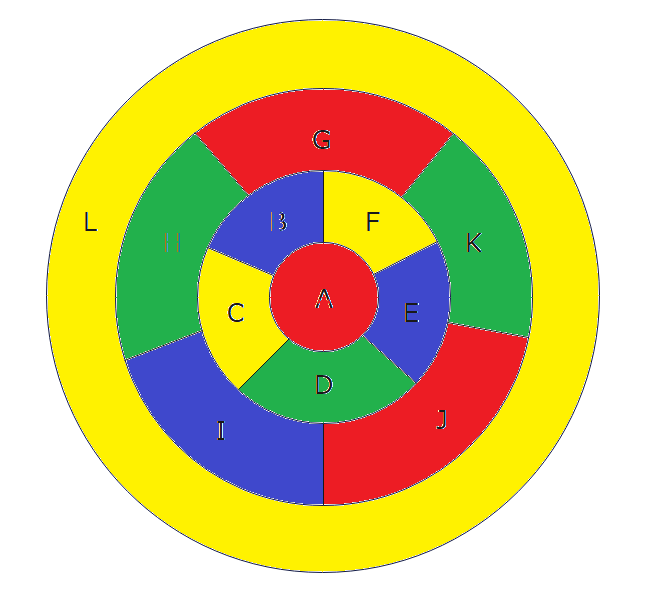
以上を整理すると、A(赤)とD(緑)の色を固定で、B~Fが2パターンでG~Kが2パターンなので、組み合わせは全4パターンになります。
3.3 順列計算方法
では、最後は計算で色の塗分け方法の場合の数を求めていきます。Aは赤色固定なので1通り。B~Fの塗り方は、Dに赤以外の3色のどれを塗るかの3通り。よって、3通り×4パターン=12通りですが、図7も8も基準している赤色がA以外に2か所あります。例えば図8であれば、Gの周りの面の色で1色なのはBの青、JだとLの黄色があるので、G、JをAの位置に持ってきたときのDに相当する色が青と黄色になるパターンが12通りの中には含まれている(重複している)ことを考慮する必要があります。
たとえば、下図9は図8でJをAの位置に持ってきてL(黄色)を図9のDの位置にした場合に該当します。
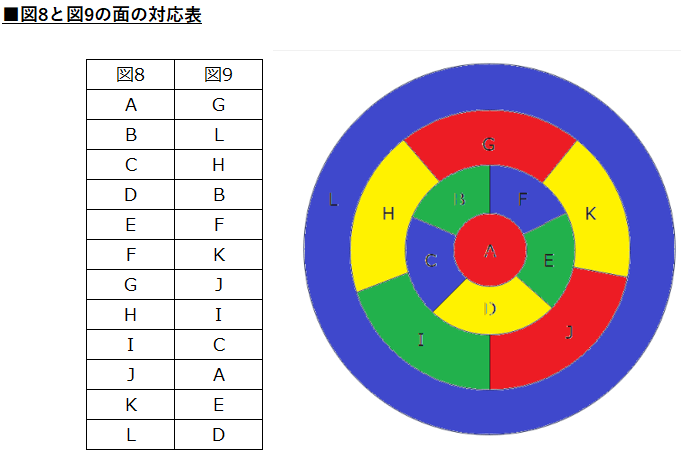
このような重複は面A、J、Gのそれぞれで3重カウントされていることになるので、求めるべきは12通り÷3=4通り。
4.まとめ
本記事では、正十二面体の各面の塗り分け問題について、立体図形を平面へ展開し、隣接関係図を描くことで平面の領域塗り分け問題へ帰着させてから解くという方法で解説をしてみました。
立体の領域塗り分け問題は、正四面体や立方体がよく扱われるテーマですが、正十二面体はなかなか空間イメージも難しいので骨の折れる問題だったのではないでしょうか。逆に、今立方体の色塗り分け問題を解いたらとっても簡単に感じるかもしれません。
「ゆっくり雑談」のカテゴリーではほかにもいろいろな数学の面白問題を扱っているので他の関連記事も興味があればぜひ確認してみてください!


コメント