【2次関数の最大・最小】定数を含む2次関数の最大値・最小値の場合分け5パターンをわかりやすく解説

今回は、定数を含む2次関数の最大値、最小値の求め方について解説していきます。2次関数の最大/最小値の求め方は分かるけど、文字が入ってきた瞬間に分からなくなってしまう、何から手を付ければいいかわからない、場合分けの考え方を知りたいなど、2次関数の最大/最小値の問題はだれもが躓く部分なので、本解説で疑問を解消していきましょう。

　本記事のレベル

重要度

低

1

2

3

4

5

高
難易度

易しい

1

2

3

4

5

難しい
暗記/理解

暗記重視

1

2

3

4

5

理解重視

【導入編】そもそも…文字が入るとなぜ難しいの？
【攻略編】2次関数の最大値・最小値問題は、場合分けしろ！
【実践編】2次関数最大最小問題解説
1. 軸が動くときの最大値と最小値の求め方
2. 範囲が変わる場合の最大値と最小値の求め方
まとめ

【導入編】そもそも…文字が入るとなぜ難しいの？

イメージできない…

2次関数の最大/最小値問題は、多くの人が躓く問題ですが、そもそもなぜ難しいのでしょうか？そんなこと聞くまでもない！と怒られそうですが、当然、文字が入っているからですよね。未知の定数を含む問題では、定数が具体的にどのような値なのか、プラスなのかマイナスなのか？大きいのか小さいのか、などが分からないため、イメージしにくく、結果として訳が分からなくなるのも無理はありません。では、少しでもイメージを膨らませるためにはどうしたらいいでしょうか？

曖昧だと考えにくい

ちょっと脱線しますが、友達から「今度旅行行くんだけど、どこがいいかなぁ」と聞かれたときを想像してみましょう。あなたなら、何と答えますか？「海鮮がおいしい北海道おすすめだよ。」、「この前、九州7県巡りが最高だったよ」とか答えますかね？でも、せっかく考えて答えたのに、友達から「あ、私海鮮苦手だから北海道はちょっと…」みたく相手の求めてたものではなかった、なんて経験ないですか？

こういう質問は、「どこに旅行するのがいいか」という質問の前提が曖昧なためこういうことが起こります。そもそも相手が、国内がいいのか、海外がいいのか、日帰りなのか、宿泊するのか、予算はどのくらいか、などによって、提案の仕方って変わりますよね？「1泊2日で大阪旅行したいんだけど、おすすめ知っている？予算は3万円くらいで！」と聞かれたら、もっと具体的な回答ができますよね。

場合分けによってイメージを具体化

$\small y=x^2+2x-5 (0 ≦ x < 5)$の最大値、最小値を求めよ、だったら解けるのに、$\small y=x^2+2ax-5a (0 ≦ x < 5)$の最大値、最小値を求めよ、となるとわからなくなってしまうのは、当たり前っちゃ当たり前です。さっきの旅行の質問の例でいうところの曖昧な質問になってしまっているので、回答者側で、国内旅行？海外旅行？予算は？などたくさん前提を考えて解答しなきゃいけません。

なので、回答するときには、「四国ならここがおすすめ」とか、「東南アジアならここがよかったよ」などの前提とともに答えたりしますね。この前提を置くという作業が、数学では場合分けになります。

【攻略編】2次関数の最大値・最小値問題は、場合分けしろ！

ここからはどのように場合分けすればいいのかを説明します。

結論から言うと、文字を含む2次関数の最大値、最小値を求めるときは、次の5パターンで場合分けすればokです。

■場合分けの最重要ポイント
2次関数の最大値、最小値を求める問題は次の5パターンで場合分け！

軸の位置が定義域の左外
軸の位置が定義域の左枠内
軸の位置が定義域の中央
軸の位置が定義域の右枠内
軸の位置が定義域の右外

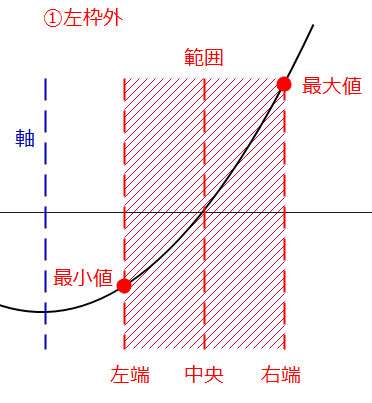
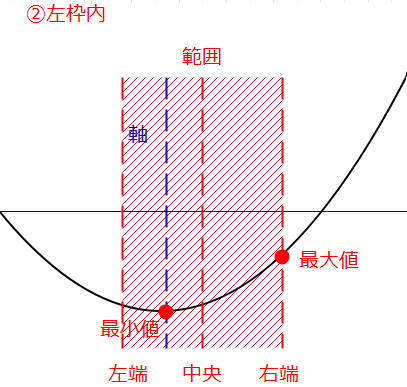
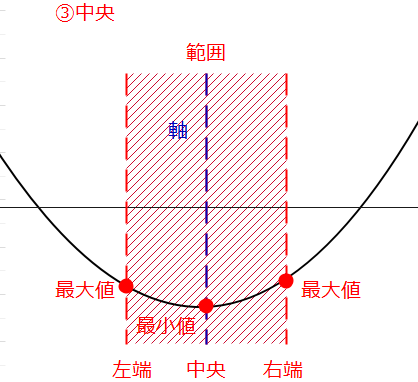
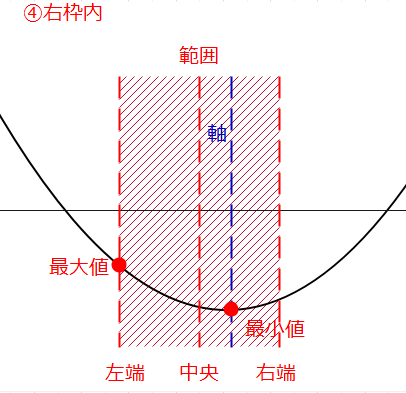
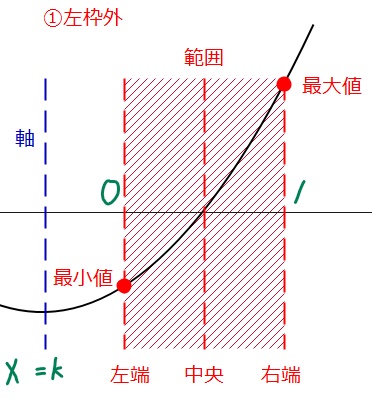
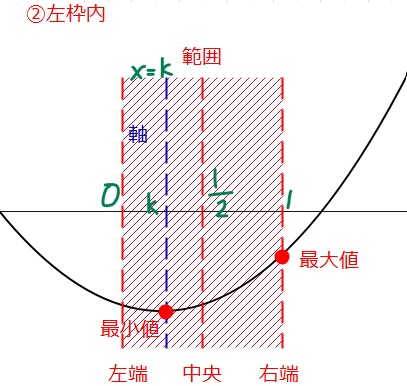
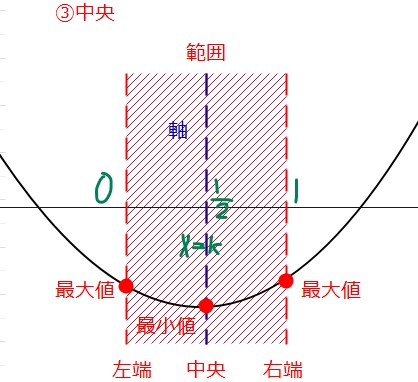
上の5つは、2次関数の軸がどの位置にあるのかというパターンで場合分けしています。1つ目の「左枠外」というのは、軸が定義域（赤枠）の左の外側にあるパターンです。2つ目は、軸が定義域の内側で、中央よりも左側にあるパターンという感じ。

この5つのパターンは、最大値と最小値がそれぞれどこになるかという組み合わせになっているので、どんな問題でもこの5つを考えていれば漏れることはありません。

後は考える問題によってパターンをまとめることもできます。たとえば、最大値だけを考えたいならば、①と②はどちらも右端で最大、④と⑤はどちらも左端で最大となることから、軸が中央より左にある場合（①＆②）、軸が中央の場合(右端と左端の2か所で最大となるので切り出して考える)、軸が中央より右にある場合（④＆⑤）の3パターンだけ考えればよいことになります。

では、実際に問題を解きながらこの5パターンを使い方を解説していきます。

【実践編】2次関数最大最小問題解説

軸が動くときの最大値と最小値の求め方

問題

$\small k$を定数とする。$\small 0≦ x ≦ 1$における関数$\small f(x)=x^2-2kx+k$について、最大値と最小値を求めよ。

解答

まずは、関数のおおよその情報を把握していきます。
関数$\small f(x)=x^2-2kx+k$を平方完成すると、 $$\small f(x)=x^2-2kx+k$$ $$\small f(x)=(x-k)^2-k^2+k$$ となることから、軸が、$\small x=k$、頂点が、($\small k,-k^2+k$)の2次関数であることが分かります。あとは、攻略編で説明した5つの場合分けで解いていきましょう。

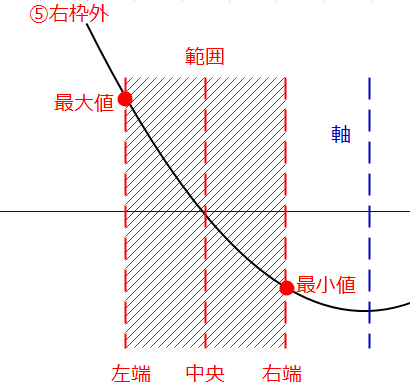
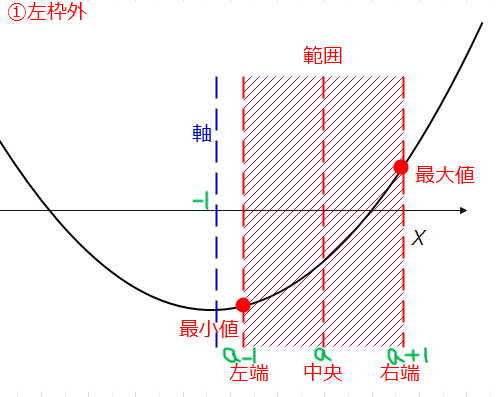
①軸が左枠外、すなわち、$\small k<0$の場合（下の図で軸$\small x=k$が0よりも左側にあるから）。

上の図には、軸と範囲$\small 0≦ x ≦ 1$を緑字で書きこんでいます。図から、$\small x=0$で最小値、$\small x=1$で最大値をとることが分かります。
$\small x=0$の値は、 $$\small f(0)=(0)^2-2・k・0+k=k（最小値）$$ $\small x=1$の値は、 $$\small f(1)=(1)^2-2・k・1+k=1-2k+k=1-k（最大値）$$ となります。

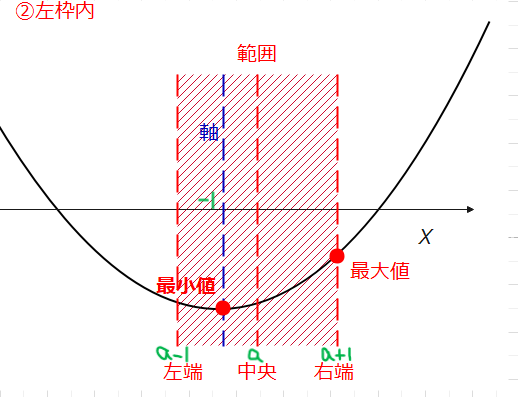
②軸が左枠内、すなわち、$\small 0≦ k < \frac{1}{2}$の場合。
（範囲「内」なので、左端は含まれるので等号ありだが、中央よりは左側を考えているので、$\small \frac{1}{2}$は含まない）。

図から、最小値は、頂点$\small x=k$の時で、$\small -k^2+k$、最大値は右端で、$\small x=1$の時で、 $\small f(1)=1-k$です。

③軸が中央、すなわち、$\small k=\frac{1}{2}$の場合。

この場合、頂点の座標は、$\small k=\frac{1}{2}$を代入すると、($\small \frac{1}{2},\frac{1}{4}$)なので、最小値は $\small x=\frac{1}{2}$で、$\small \frac{1}{4}$、最大値は、$\small x=0,1$で、$\small f(0)=f(1)=\frac{1}{2}$です（中央に軸があるときは、左右対称なので、最大値は、両端で一緒になります）。

④軸が右枠内、すなわち、$\small \frac{1}{2}< k ≦ 1$の場合。

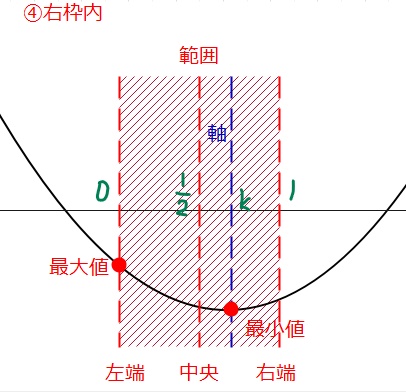
最小値は、頂点なので、$\small x=k$で、$\small -k^2+k$。最大値は、左端なので、$\small x=0$で、$\small f(0)=k$。

⑤軸が右枠外、すなわち、$\small 1 < k $の場合。

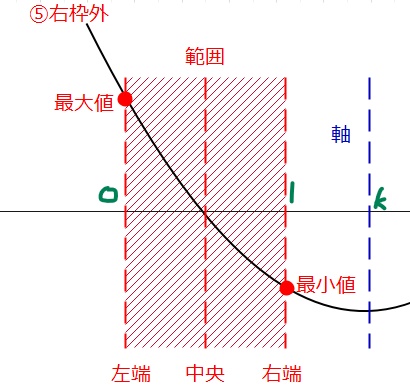
$\small x=0$で最大値、$\small f(0)=k$、$\small x=1$で最小値、$\small f(1)=1-k$となります。

よって、①～⑤をまとめると、答えは以下の通りになります。
【解答】
$\small k<0$のとき、 $\small x=1$で最大値、$\small 1-k$、$\small x=0$で最小値、$\small k$

$\small 0≦ k < \frac{1}{2}$のとき、 $\small x=1$で最大値、$\small 1-k$、$\small x=k$で最小値、$\small -k^2+k$

$\small k=\frac{1}{2}$のとき、 $\small x=0,1$で最大値、$\small \frac{1}{2}$、$\small x=\frac{1}{2}$で最小値、$\small \frac{1}{4}$

$\small \frac{1}{2}< k ≦ 1$のとき、 $\small x=0$で最大値、$\small k$、$\small x=k$で最小値、$\small -k^2+k$

$\small 1 < k $のとき、 $\small x=0$で最大値、$\small k$、$\small x=1$で最小値、$\small 1-k$

範囲が変わる場合の最大値と最小値の求め方

問題

$\small a$を定数とする。$\small a-1 ≦ x ≦ a+1$における関数$\small f(x)=x^2+2x-2$について、以下を求めよ。
(1)最大値
(2)最小値

解答

今回は、2次関数が分かっていて、代わりに定義域に定数が含まれています。
範囲が変わる場合も、考え方は同じです。範囲と軸の位置関係から、5パターンに当てはめて考えていきます。
2次関数を平方完成すると、$\small f(x)=x^2+2x-2=(x+1)^2-3$なので、軸が$\small x=-1$、頂点が(-1,-3)であることが分かります。では、最大値、最小値を5つのパターンに分けて図式化してみます。

(1)
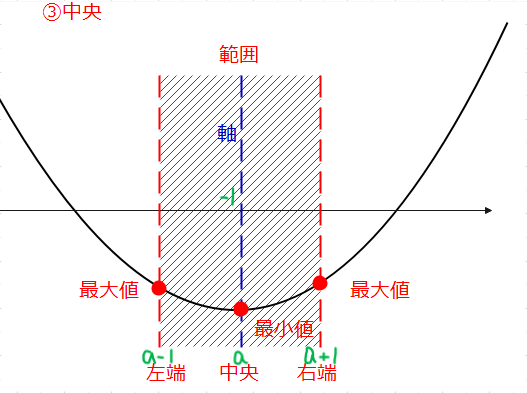
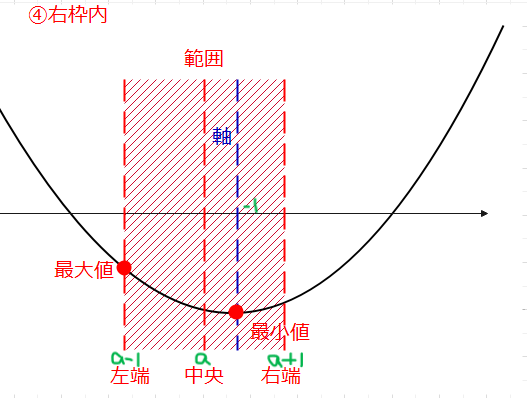
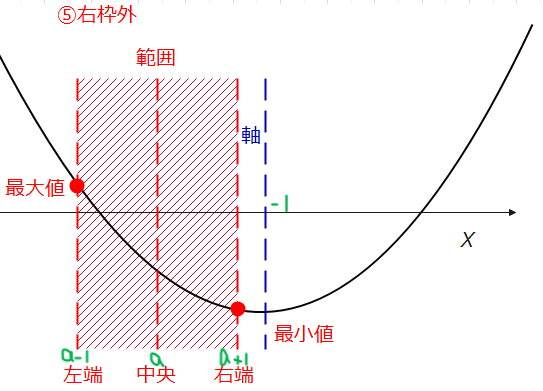
5つの図で、最大値がどこになるかを見てください。
①②では、右端（$\small x=a+1$）、③では、両端（$\small x=a-1、a+1$）、④⑤では、左端($\small x=a-1$)です。なので、その3パターンに分けてあげればよいのです。
では、次は3つのパターンは、それぞれ、定数$\small a$がどのような場合のことか考えます。まず、①②を見ると、軸$\small x=-1$が中央の$\small x=a$よりも左側にありますね。左枠外と左枠内の場合なので、枠の内外に関係なく、中央より左側に軸があるってことです。これを数式で表すと、$\small -1 < a $となります。次に、③は、$\small x=a$と軸$\small x=-1$が重なった時なので、$\small a=-1$の場合です。最後に、④⑤について、軸$\small x=-1$が中央$\small x=a$より右側にある場合なので、$\small a < -1 $です。これで、場合分けの準備はできたので、実際にそれぞれの場合で最大値を求めます。
(i)$\small -1 < a $の場合
$\small x=a+1 $の時に、最大値をとり、その値は、
$$\small f(a+1)=(a+1)^2+2・(a+1)-2=a^2+2a+1+2a+2-2=a^2+4a+1$$ である。
(ii)$\small a=-1$の場合
両端、すなわち、$\small x=-2,0$で最大値をとり、その値は、 $$\small f(-2)=f(0)=(0)^2+2・(0)-2=-2$$ ※$\small a=-1$なので、$\small a$に-1を代入して値を求めるのを忘れないようにする。
(iii)$\small a < -1 $の場合
$\small x=a-1 $の時に、最大値をとり、その値は、
$$\small f(a-1)=(a-1)^2+2・(a-1)-2=a^2-2a+1+2a-2-2=a^2-3$$ である。

【解答】
$\small -1 < a $の場合、$\small x=a+1 $の時に、最大値、$\small a^2+4a+1$、
$\small a=-1$の場合、$\small x=-2,0$で最大値、$\small -2$、
$\small a < -1 $の場合、$\small x=a-1 $の時に、最大値、$\small a^2-3$。

(2)
次は最小値を求めます。①～⑤の図をみて、どこが最小値になっているかを整理しましょう。
①は、$\small x=a-1$、②～④は、$\small x=a$、⑤は、$\small x=a+1$で最小になっているのでこの3パターンで場合分けします。
(i)$\small -1 < a-1$、すなわち、$\small 0 < a$の場合
$\small x=a-1$で最小値$\small a^2-3$をとる。
(ii)②～④の場合
②～④の場合というのは、軸、$\small x=-1$が$\small a-1$～$\small a+1$の範囲にある場合で、条件式で書くと、$\small a-1 ≦ -1 ≦ a+1$のようになります。
あまり見かけない不等式ですが、左右で分けて考えればよいです。
$\small a-1 ≦ -1 $を解くと、$\small a ≦ 0$、$\small -1 ≦ a+1$を解くと、$\small -2 ≦ a$なので、合わせると、$\small -2 ≦ a ≦ 0$となります。なので、(ii)で考える$\small a$の範囲は、$\small -2 ≦ a ≦ 0$の場合です。この場合は、$\small x=-1$で最小値は、$\small -3$です。
(iii)$\small a+1 < -1$の場合、すなわち、$\small a < -2$の場合
$\small x =a+1$で最小値、$\small a^2+4a+1$をとる。

【解答】
$\small 0 < a $の場合、$\small x=a-1 $の時に、最小値、$\small a^2-3$、
$\small -2 ≦ a ≦ 0$の場合、$\small x=-1$で最小値、$\small -3$、
$\small a < -2 $の場合、$\small x=a+1 $の時に、最小値、$\small a^2+4a+1$。