今回は3次方程式に関する問題として、1の3乗根(ω)の性質を利用した式の値や実数解・虚数解の性質や解の条件などから方程式の係数を決定してく問題について解説していきたいと思います。
1の3乗根の問題は意外と簡単そうに見えて問題になると解けなくなってしまう人も多いので、解き方の思考法や着眼すべきポイントについてわかりやすく説明していきたいと思います。
3次方程式の係数決定については、2次方程式のときのように判別式があるわけではないので、解き方のアプローチも全然変わってきます。改めてどんな思考法で解いていけばよいのか本記事を通して理解していきましょう。
では早速問題演習に移りましょう!
- 1の3乗根(ω)の性質を理解したい人
- 3乗根の性質を利用した問題の解き方のコツを知りたい人
- 3次方程式の解の条件から係数決定するコツを知りたい人
- 定期テスト対策、大学受験対策がしたい人
【問題&解説】1の3乗根(ω)の性質を利用した問題
【問題1】1の3乗根が含まれた式の値(難易度:★☆☆)
方程式 \(\small x^3=1\)の虚数解の1つを\(\small \omega\)とするとき、次の値を求めよ。
(1)\(\small \omega^{40}+\omega^{38}\)
(2)\(\small \displaystyle \frac{1}{\omega^2}+\frac{1}{\omega}+\omega+\omega^2\)
(3)\(\small 1+\omega+\omega^2+\omega^3+\cdots+\omega^{59}+\omega^{60}\)
(4)\(\small (\omega+2\omega^2)^2+(2\omega+\omega^2)^2\)
(5)\(\small (1-\omega)(1-\omega^2)(1-\omega^4)(1-\omega^5)\)
【性質1】 \(\small \omega^3=1\)
【性質2】 \(\small \omega^2=-\omega-1\)
を利用して次数下げせよ!
\begin{split}
&\small x^3-1=0\\
\small \Leftrightarrow \space &\small (x-1)(x^2+x+1)=0 \space \cdots (*)\\
\end{split}
を解くことで、\(\small x=1\), \(\small \displaystyle \frac{-1-\sqrt{3}i}{2}\), \(\small \displaystyle \frac{-1+\sqrt{3}i}{2}\)の3つと求めることができるが、これらを1の3乗根という。
・1の3乗根の虚数解は2個あるので虚数解の1つを\(\small \omega\)とおくと、\(\small \omega\)は方程式\(\small (*)\)の\(\small x^2+x+1=0\)を解くことで出てくる解なので、
$$\small \omega^2+\omega+1=0 \space \cdots 【性質2】$$
を満たす。また、\(\small x^3=1\)の解でもあるので当然
$$\small \omega^3=1 \space \cdots【性質1】$$
も満たす。
\(\small \omega\)は1の3乗根なので、\(\small \omega^3=1\)を満たす。
よって、
\begin{split}
\small \omega^{40}+\omega^{38} &\small =\omega^{39}\cdot \omega + \omega^{36} \cdot \omega^2\\
&\small =(\color{#ef5350}{\omega^3})^{13}\cdot \omega +(\color{#ef5350}{\omega^3})^{12} \cdot \omega^2\\
&\small =\color{#ef5350}1^{13}\cdot \omega +\color{#ef5350}1^{12} \cdot \omega^2\\
&\small =\omega +\omega^2 \space \cdots ①\\
\end{split}
①はだいぶ簡単な式になったが、\(\small \omega^2\)の項があるので1乗以下の項に次数下げしたい。ここで、\(\small \omega\)は\(\small x^3=1\)の虚数解なので、
\begin{split}
&\small x^3-1=0\\
\small \Leftrightarrow \space &\small (x-1)(x^2+x+1)=0\\
\end{split}
上記の方程式で2次方程式 \(\small x^2+x+1=0\)を解くことで出てくる解の1つが\(\small \omega\)であることから、\(\small \omega\)は\(\small \omega^2+\omega+1=0\)を満たす[*1]。
*1:補足
当然ながら方程式の解を該当の方程式に代入すればその方程式を満たす。
例として\(\small x^2-4x+3=0\)の解は\(\small x=-1,-3\)であるが、たとえば\(\small x=-1\)を2次方程式に代入すると
\begin{split}
&\small x^2-4x+3\\
&\small \Rightarrow \space (-1)^2-4\cdot (-1)+3=1-4+3=0\\
\end{split}
となり\(\small x^2-4x+3=0\)を満たす(\(\small x=-3\)についても同様)。
なので、今回であれば、\(\small x^2+x+1=0\)の解が\(\small \omega\)であることから\(\small \omega^2+\omega+1=0\)を満たすということ。
よって、\(\small \omega^2+\omega+1=0 \space \Leftrightarrow \space \omega^2=-\omega-1\)(次数下げ)を①に代入することで
\begin{split}
\small \omega +\color{#ef5350}{\omega^2} &\small = \omega +\color{#ef5350}{(-\omega -1)}\\
&\small = \color{red}{-1 \space \cdots 【答】}
\end{split}
1の3乗根の虚数解 \(\small \omega\)は \(\small \omega^2+\omega+1=0\) ⇔ \(\small \omega^2=-\omega-1\)を満たすことより
\begin{split}
&\small \displaystyle \frac{1}{\omega^2}+\frac{1}{\omega}+\omega+\color{red}{\omega^2}\\
&\small \displaystyle =\frac{\color{#5c6bc0}{1+\omega}}{\omega^2}+\omega+\color{red}{(-\omega-1)}\\
&\small \displaystyle =\frac{\color{#5c6bc0}{-\omega^2}}{\omega^2}-1 \quad \color{#5c6bc0}{◀\omega+1=-\omega^2を利用}\\
&\small \displaystyle =-1-1\\
&\small \displaystyle =\color{red}{-2 \space \cdots 【答】}\\
\end{split}
\begin{split}
&\small \omega^2+\omega+1=0\\
&\small \omega^2+\omega=-1\\
&\small \omega^2=-\omega-1\\
&\small \omega^2+1=-\omega\\
\end{split}
など、どこまでを右辺に移項するかでいろいろな形で使える!
●別解
分数型は\(\small \omega^3=1\)を利用して分数を解消すると計算が楽である。
\begin{split}
&\small \displaystyle \frac{1}{\omega^2}+\frac{1}{\omega}+\omega+\omega^2\\
\small =&\small \displaystyle \frac{\color{#ef5350}{\omega^3}}{\omega^2}+\frac{\color{#ef5350}{\omega^3}}{\omega}+\omega+\omega^2 \space \color{#ef5350}{◀\omega^3=1を利用}\\
\small =&\small \color{#ef5350}{\omega}+\color{#ef5350}{\omega^2}+\omega+\omega^2\\
\small =&\small 2(\omega+\omega^2)\\
\small =&\small 2\cdot (-1)\\
\small =&\small \color{red}{-2 \space \cdots 【答】}\\
\end{split}
●考察
\(\small \omega\)の指数が1ずつ大きくなるような和であることに注目すると、\(\small \omega\)は \(\small \omega^2+\omega+1=0\) を満たすことから、両辺に追加で\(\small \omega\)を掛け算したような式はすべて0になることに着目する。
\begin{split}
&\small \omega^3+\omega^2+\omega = \omega\color{#ef5350}{(\omega^2+\omega+1)}=\color{#ef5350}0\\
&\small \omega^4+\omega^3+\omega^2 = \omega^2\color{#ef5350}{(\omega^2+\omega+1)}=\color{#ef5350}0\\
&\small \omega^{10}+\omega^9+\omega^8 = \omega^8\color{#ef5350}{(\omega^2+\omega+1)}=\color{#ef5350}0\\
&\small \cdots
\end{split}
1の3乗根の虚数解 \(\small \omega\)は \(\small \omega^2+\omega+1=0\) を満たすことより
\begin{split}
&\small 1+\omega+\omega^2+\omega^3+\cdots+\omega^{59}+\omega^{60}\\
&\small =1+(\omega+\omega^2+\omega^3)+\cdots\\
&\small \quad \cdots+(\omega^{58}+\omega^{59}+\omega^{60})\\
&\small =1+\omega\color{#ef5350}{(1+\omega+\omega^2)}+\cdots\\
&\small \quad \cdots+\omega^{58}\color{#ef5350}{(1+\omega+\omega^2)} \quad \color{#ef5350}{◀0になる形を作り出す}\\
&\small =1+\omega\cdot \color{#ef5350}{0}+\cdots+\omega^{58}\cdot \color{#ef5350}{0}\\
&\small =\color{red}{1 \space \cdots 【答】}\\
\end{split}
1の3乗根の虚数解 \(\small \omega\)は\(\small \omega^2+\omega+1=0\) ⇔ \(\small \omega^2=-\omega-1\) を満たすことより\(\small \omega^2\)を次数下げしてから展開する。
\begin{split}
&\small (\omega+2\color{#ef5350}{\omega^2})^2+(2\omega+\color{#ef5350}{\omega^2})^2\\
&\small =\{\omega+2\color{#ef5350}{(-\omega-1)}\}^2+\{2\omega+\color{#ef5350}{(-\omega-1)}\}^2\\
&\small =(-\omega-2)^2+(\omega-1)^2\\
&\small =(\omega^2+4\omega+4)+(\omega^2-2\omega+1)\\
&\small =2\color{#ef5350}{\omega^2}+2\omega+5\\
&\small =2\color{#ef5350}{(-\omega-1)}+2\omega+5 \quad \color{#ef5350}{◀再び次数下げ}\\
&\small =-2\omega-2+2\omega+5\\
&\small =\color{red}{3 \space\cdots【答】}\
\end{split}
1の3乗根の虚数解 \(\small \omega\)は \(\small \omega^3=1\)、\(\small \omega^2+\omega+1=0\)を満たすので、
\begin{split}
&\small (1-\omega)(1-\omega^2)(1-\omega^4)(1-\omega^5)\\
=&\small (1-\omega)(1-\omega^2)(1-\omega\cdot \color{#ef5350}{\omega^3})(1-\omega^2 \cdot \color{#ef5350}{\omega^3})\\
=&\small (1-\omega)^2(1-\color{#5c6bc0}{\omega^2})^2\\
=&\small (1-\omega)^2(1-\color{#5c6bc0}{(-\omega-1)})^2\\
=&\small (\omega-1)^2(\omega+2)^2\\
=&\small (\color{#5c6bc0}{\omega^2}+\omega-2)^2\\
=&\small (\color{#5c6bc0}{(-\omega-1)}+\omega-2)^2\\
=&\small (-3)^2\\
=&\small \color{red}{9 \space \cdots 【答】}\\
\end{split}
【問題2】1の3乗根を利用した整式の余り(難易度:★★☆)
整式 \(\small x^{2019}+x^{2020}\)を整式 \(\small x^2+x+1\)で割った余りを求めよ。
[広島工業大]
・整式の余りを求める問題を解く際の考え方については、【剰余の定理】すぐに使える裏ワザ紹介!基礎~難問までパターン別に解説(重解・虚数解ωの余りの計算)をチェックしておきましょう。
1の3乗根のうち虚数解の1つを\(\small \omega\)とおくと、
\begin{split}
&\small \omega^3=1\\
\small \Leftrightarrow \space &\small \omega^3-1=0\\
\small \Leftrightarrow \space &\small (\omega-1)(\omega^2+\omega+1)=0\\
\end{split}
\(\small \omega\)は虚数解なので\(\small \omega \neq 1\)より、
$$\small \omega^2+\omega+1=0$$
を満たす。
さて、除算する式が2次式であることから余りは1次式以下となるため、整式 \(\small x^{2019}+x^{2020}\)を整式\(\small x^2+x+1\)で割った余りを\(\small ax+b\)、商を\(\small Q(x)\)とおくと、
\begin{split}
&\small x^{2019}+x^{2020} = (x^2+x+1)Q(x)+ax+b\\
\end{split}
より、両辺に\(\small x=\omega\)を代入すると
\begin{split}
&\small \omega^{2019}+\omega^{2020} = \color{#ef5350}{(\omega^2+\omega+1)}Q(\omega)+a\omega+b\\
\small \Leftrightarrow \space &\small (\color{#5c6bc0}{\omega^3})^{673}+(\color{#5c6bc0}{\omega^3})^{673}\cdot \omega = \color{#ef5350}0 \cdot Q(\omega)+a\omega+b\\
\small \Leftrightarrow \space &\small \color{#5c6bc0}1^{673}+\color{#5c6bc0}1^{673}\cdot \omega =a\omega+b\\
\small \Leftrightarrow \space &\small 1+\omega =a\omega+b\\
\end{split}
上式について、\(\small \omega\)は虚数であることから、両辺を係数比較することで、\(\small a=1\), \(\small b=1\) [*1].
よって、余りは\(\small x+1\)…【答】(求める余りを\(\small ax+b\)とおいていたので).
*1:【補足】虚数の係数比較について
本来であれば、虚数の係数比較は『虚数が等しい ⇔ 実部同士、虚部同士が等しい』という関係が成り立つことを利用するが、本問の解説では\(\small \omega\)自体が虚数なので、厳密には実部同士/虚部同士の比較になっていない。ただ直感的にもわかる通り両辺に共通の虚数があるため、結果としては\(\small \omega\)の係数と実数部分を比較しても問題はない。
厳密さを求めるのであれば本来の考え方に立ち返って、以下のような実部と虚部を比較する論証をするとよいだろう。
\(\small \omega = x+iy\)(ただし\(\small x,y \neq 0\)は実数で、\(\small i\)は虚数単位)とおくと
\begin{split}
&\small 1+\omega =a\omega+b\\
\small \Leftrightarrow \space &\small \omega(a-1) +(b-1)=0\\
\small \Leftrightarrow \space &\small (x+iy)(a-1) +(b-1)=0\\
\small \Leftrightarrow \space &\small \color{#ef5350}{[(a-1)x+(b-1)]}+\color{#5c6bc0}{(a-1)y}i=0\\
\end{split}
上式が成り立つためには、実部と虚部が0になる必要があるので、\(\small a-1=0\), \(\small (a-1)x+(b-1)=0\)を解くことで、\(\small a=b=1\)を得る。
【問題&解説】3次方程式の解の条件
【問題3】実数解・虚数解からの係数決定(難易度:★☆☆)
(1)3次方程式 \(\small x^3-4x^2+ax+6=0\)の1つの解が\(\small -1\)のとき、定数 \(\small a\)の値と他の2つの解を求めよ。
(2)3次方程式 \(\small x^3+ax^2+8x+b=0\)が\(\small 1+i\)を解に持つとき、実数 \(\small a,b\)の値を求めよ。ただし\(\small i\)を虚数単位とする。
(1)[摂南大]、(2)[立教大 改題]
・既知の解が虚数解の場合は、方程式に代入すると計算が煩雑になるため、共役な複素数が満たす2次方程式を因数として、もとの3次方程式を因数分解する解法がおすすめ。
\(\small x=-1\)が方程式の解であることから、問題の方程式に代入することで
\begin{split}
&\small (-1)^3-4\cdot (-1)^2+a\cdot(-1)+6=0\\
\small \Leftrightarrow \space &\small -a+1=0\\
\small ∴ \space &\small \color{red}{a=1 \space \cdots【答】}\\
\end{split}
3次方程式が \(\small x^3-4x^2+x+6=0\)と求まったので、あとは因数分解することで他の解を求めていく。\(\small x=-1\)が解であることから、\(\small x+1\)を因数に持つので
\begin{split}
&\small x^3-4x^2+x+6=0\\
\small \Leftrightarrow \space &\small (x+1)(x^2-5x+6)=0 \space [*1]\\
\small \Leftrightarrow \space &\small (x+1)(x-2)(x-3)=0\\
\small ∴ \space &\small x=-1,2,3\\
\end{split}
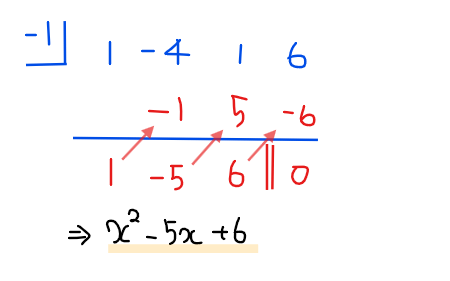
*1:【補足】高次方程式の因数分解について
高次方程式の因数分解をする際は組立除法の利用が王道だが、あまり使っていないとやり方を忘れてしまうこともあるため、個人的には\(\small x\)の係数を見ながら因数分解する方法をおすすめする。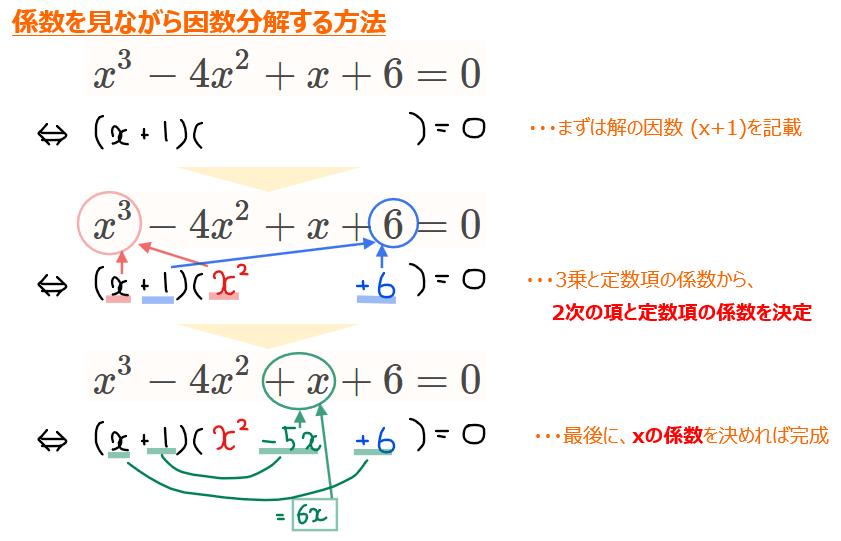
慣れると上記の解き方の方が素早く因数分解ができる。
よって、\(\small -1\)以外の解は、\(\small x=2, \space 3\)…【答】.
\(\small x=1+i\)を3次方程式の解に持つということは、共役な複素数[*1]である\(\small x=1-i\)も解となることから、
*1:【補足】共役な複素数とは
ある複素数に対して、虚数単位\(\small i\)を\(\small -i\)に置き換えた複素数を共役な複素数という。
解と係数の関係より、\(\small x=1\pm i\)を2解に持つ2次方程式は \(\small x^2-2x+2=0\) [*2]を満たす。
*2:補足
2解の和が \(\small (1+i)+(1-i)=2\)、2解の積が \(\small (1+i)(1-i)\)\(\small =1-i^2=1-(-1)=2\)より、解と係数の関係から、2解の和の符号を変えたものが\(\small x\)の係数、2解の積が定数項になる。
よって、問題の3次方程式は
\begin{split}
&\small x^3+ax^2+8x+b=0\\
\small \Leftrightarrow \space &\small (x^2-2x+2)(x+p)=0\\
\end{split}
のように因数分解できることになる。このように因数分解できるためには
\begin{split}
&\small x^3+ax^2+8x+b=(x^2-2x+2)(x+p)\\
\end{split}
が成り立てばよいので、\(\small x^3+ax^2+8x+b\)を \(\small x^2-2x+2\)で割り算した余りが「0」 [*3] となっている必要がある。
*3:【補足】因数分解と余りの関係
整式が因数分解できるとは、整式を因数で割り算したときの余りが0ということ。
●整式の割り算の基本性質
整式を\(\small P(x)\)、割り算する整式\(\small A(x)\)、商を\(\small Q(x)\)、余りを\(\small R(x)\)とすると、
$$\small P(x) = A(x)Q(x)+R(x)$$
が成り立つ。
特に \(\small R(x)=0\)(余りが0)の場合、上式は
$$\small P(x) = A(x)Q(x)$$
となり、因数分解できるという(因数分解とは和を積の形で表すこと)。
※具体例を挙げると、\(\small P(x)=x^2+x-6\)、\(\small A(x)=x-2\)、\(\small Q(x)=x+3\)とした場合、\(\small P(x) = A(x)Q(x)\) は\(\small x^2+x-6=(x-2)(x+3)\)と表せるので、まさに因数分解そのものである。
余りの式を整式の筆算で計算すると
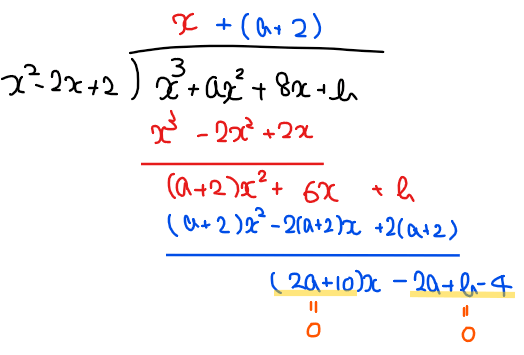
故に、余りが「0」、すなわち \(\small (2a+10)x-2a+b-4 = 0\)が\(\small x\)の値に関係なく常に成り立つ[*3]ためには、\(\small x\)の係数と定数項がそれぞれ0であればよいので、
\begin{cases}
\small 2a+10=0\\
\small -2a+b-4=0\\
\end{cases}
*3:【補足】恒等式が成り立つ条件
\(\small x^3+ax^2+8x+b\)が \(\small (x^2-2x+2)(x+p)\)のように因数分解できるためには、\(\small x^3+ax^2+8x+b=(x^2-2x+2)(x+p)\)が成り立つ必要があるが、この関係式は『方程式』ではなく『恒等式』であることに注意が必要。
恒等式が0になる場合、『各文字の係数(定数項も含む)=0』が成り立つ。
*方程式とは…
未知の文字の値を求めるために等しい関係を等号で結んだ式。
例)\(\small 3x-2=x+6 \space …etc\)
*恒等式とは…
端的に言えば計算式のこと(ただの式変形)。
例)\(\small 3(2x-4)=6x-12 \space …etc\)
これを解くと、\(\small a=-5, \space b=-6\)…【答】を得る。
●別解:筆算をせずに定数を求める解法
\(\small x^3+ax^2+8x+b=(x^2-2x+2)(x+p)\)を恒等式として解くことで定数\(\small a,b\)を求めることも可能である(筆算が不要なので若干計算が楽かも…)。
求め方としては、まず左辺の\(\small x\)の係数が8であることから、右辺の展開で\(\small x\)の係数に関連する項だけ計算すると、\(\small (-2x)\cdot p + 2\cdot x =(2-2p)x\)となるので、係数比較より、
\begin{split}
&\small 2-2p = 8\\
\small \Leftrightarrow \space &\small -2p = 6\\
\small ∴ \space &\small p = -3\\
\end{split}
よって、\(\small x^3+ax^2+8x+b=(x^2-2x+2)(x-3)\)の形に因数分解できることが分かったので、あとは\(\small x^2\)と定数項に関連する項だけ展開してあげれば\(\small a,b\)の値を求めることができる。
※因数分解できるとは割り算の余りが0ということ!
【問題4】3次方程式と解の条件(難易度:★★★)
(1)3次方程式 \(\small x^3+(a-2)x^2-4a=0\)が2重解を持つように、定数\(\small a\)の値を定めよ。
(2)\(\small n\)を自然数とする。\(\small x\)について3次方程式 \(\small x^3+nx^2+(n-6)x-2=0\)の1つの解が自然数であるとき、自然数の解と他の2解を求めよ。
[(1)東北学院大 類題、(2)立命館大 改題]
・(1)で解が2重解を持つ条件ということは、3次方程式が\(\small (x-\alpha)(x-\beta)^2=0\)(\(\small \alpha \neq \beta\))の形に因数分解できることを意味している。つまり、\(\small x=\alpha\)の解を見つけて因数分解できれば、残りの2次方程式部分については判別式の条件が利用可能。ただし、2重解を持つ条件は2次方程式部分が重解になるパターンだけではないことに注意が必要。
・(2)は自然数解を持つ条件を求める問題なので、整数問題では定石の積の形に落とし込む方針で式変形する。
3次方程式の3つの解のうち2つが同じ解(重解)になるような\(\small a\)の値を求める。2次方程式であれば「重解を持つ ⇔ 『判別式=0』」という条件式があったが、3次方程式以上になると一般に重解を持つ条件式はないので、うまく因数分解していくことを考える。
因数分解する際は次数の低い文字に着目して整理することが王道なので、今回であれば\(\small a\)について整理すると、
\begin{split}
&\small x^3+(a-2)x^2-4a=0\\
\small \Leftrightarrow \space &\small (x^2-4)a+x^3-2x^2=0\\
\small \Leftrightarrow \space &\small (x-2)(x+2)a+x^2(x-2)=0\\
\small \Leftrightarrow \space &\small (x-2)\{(x+2)a+x^2\}=0\\
\small \Leftrightarrow \space &\small \color{#ef5350}{(x-2)}\color{#5c6bc0}{(x^2+ax+2a)}=0 \space \cdots (*)\\
\end{split}
\(\small (*)\)が2重解を持つためには、『(A)青色箇所の2次方程式が\(\small x\neq 2\)の2重解を持つ』または、『(B)青色箇所の2次方程式の1つの解のみが\(\small x=2\)を持つ』の2パターンがある。
●補足
2重解を持つ可能性は、(A)のみではなく(B)のように\(\small x=2\)が2重解になるパターンもあることに注意しよう。
(A) 青色箇所の2次方程式が\(\small x \neq 2\)の2重解を持つ場合
2次方程式 \(\small x^2+ax+2a=0\)が2重解を持つことから、判別式 \(\small D=0\)より
\begin{split}
\small D = &\small a^2-4\cdot 1 \cdot 2a= 0\\
\small \Leftrightarrow \space &\small a^2-4\cdot 1 \cdot 2a= 0\\
\small \Leftrightarrow \space &\small a(a-8)=0\\
\small ∴ \space &\small a=0,\space 8\\
\end{split}
このとき、\(\small a=0, \space 8\)で\(\small (*)\)の2重解が\(\small x \neq 2\)であることを確認しておく。
\(\small a=0\)のとき\(\small (*)\)は
\begin{split}
&\small x^2(x-2)=0\\
\small ∴ \space &\small x=2,\space 0\\
\end{split}
よって、確かに\(\small x=0\)の2重解を持つ。
同様に\(\small a=8\)のときは
\begin{split}
&\small (x-2)(x^2+8x+16)=0\\
\small \Leftrightarrow \space &\small (x-2)(x+4)^2=0\\
\small ∴ \space &\small x=2,\space -4\\
\end{split}
よって、確かに\(\small x=-4\)の2重解を持つ。
よって、\(\small a =0, \space 8\)は問題の条件を満たす…①。
(B) 青色箇所の2次方程式の1つの解のみが\(\small x=2\)を持つ場合
\(\small x^2+ax+2a=0\)の2つの解のうち1つが \(\small x=2\)を解に持つことから
\begin{split}
\small 2^2+ &\small 2a+2a=0\\
\small \Leftrightarrow \space &\small 4a=-4\\
\small ∴ \space &\small a=-1\\
\end{split}
逆に、\(\small a=-1\)のとき、\(\small (*)\)の3次方程式は [*1]、
\begin{split}
&\small (x-2)(x^2-x-2)=0\\
\small \Leftrightarrow \space &\small (x-2)^2(x+1)=0\\
\small ∴ \space &\small x=2, \space -1\\
\end{split}
よって、\(\small x=2\)が2重解となることから\(\small a=-1\)は問題の条件を満たす…②。
*1:【補足】「逆に…」の論証ってなんで必要?
\(\small x^2+ax+2a=0\)が\(\small x=2\)を解を持つときの\(\small a\)の値を求めたにも拘らず、なぜわざわざ求めた\(\small a \)の値で3次方程式が2重解を持つかどうかを確認する必要があるのだろうか?
その理由としては、\(\small x=2\)を\(\small x^2+ax+2a=0\)に代入することで分かるのは、2解のうち少なくとも1つは\(\small x=2\)であるということまでであり、2解のうち1つだけが\(\small x=2\)ということまでは確認できないからである。もし、他の解も\(\small x=2\)であった場合、問題の3次方程式が\(\small x=2\)で3重解を持ってしまうため、実際に3次方程式の解を求めて3重解になっていないことを確認する必要があることに注意しよう。
※ちなみに(A)で\(\small x^2+ax+2a=0\)が重解を持つ条件は\(\small a =0,8\)と求めているので、\(\small a=-1\)では重解は持たない ⇔ 他の解は\(\small x \neq 2\)であるという論証ももちろんOKである。
以上より、\(\small (*)\)が2重解を持つためには、(A)または(B)のいずれか満たせばよいので、①、②の合計範囲を求めればよい。
よって、\(\small a=-1,\space 0,\space 8 \space \cdots 【答】\).
問題の3次方程式が持つ自然数の解を\(\small x=m\)とおく。\(\small m\)が満たすべき条件を絞りこむために、問題の3次方程式を整数の積の形に因数分解することを考える(整数問題では割と典型的な解法)。
\begin{split}
&\small m^3+nm^2+(n-6)m-2=0\\
\small \Leftrightarrow \space &\small (m^2+m)n+m^3-6m-2=0 \quad \color{#ef5350}{◀最低次数の文字について整理}\\
\small \Leftrightarrow \space &\small m(m+1)n+m^3-6m-2=0\\
\small \Leftrightarrow \space &\small m\{(m+1)n+m^2-6\}=2 \quad \cdots (*)\\
\end{split}
ここで、\(\small m\)は自然数かつ \(\small (m+1)n+m^2-6\)は整数[*1]であることから、\(\small (*)\)の左辺は(自然数)×(整数)となる。『(自然数)×(整数)= 2 』になる自然数は1または2しかないことから、式を満たす自然数と整数の組合せは『(自然数, 整数)\(\small =(1,2), \space (2,1)\)』に絞り込みができる。
*1:\(\small (m+1)n+m^2-6\)が整数となる理由
\(\small m, \space n\)は自然数なので、\(\small (m+1)n+m^2-6\)自体は、自然数同士の和差積の計算であるため、全体としても自然数または整数になる。
また、\(\small m, \space n≧1\)が成り立つことから
\begin{split}
\small (m+1)n+m^2-6 &\small ≧(1+1)\cdot 1+1^2-6\\
&\small =2+1-6\\
&\small =-3\\
\end{split}
と不等式評価できることから、値としては-3以上(負になる可能性もある)なので整数となる。
ゆえに、
$$\small (m, \space (m+1)n+m^2-6) = (1,2), \space (2,1)$$
[1] \(\small (m, \space (m+1)n+m^2-6) = (1,2)\)の場合
\(\small m=1\)を\(\small (m+1)n+m^2-6=2\)に代入することで、
\begin{split}
\small (1+1)n &\small +1^2-6=2\\
\small \Leftrightarrow \space &\small 2n-5 = 2\\
\small ∴ \space &\small \displaystyle n = \frac{7}{2}\\
\end{split}
これは\(\small n\)が自然数という問題の条件に反するため不適。
[2] \(\small (m, \space (m+1)n+m^2-6) = (2,1)\)の場合
同様に\(\small m=2\)を\(\small (m+1)n+m^2-6=1\)に代入することで、
\begin{split}
\small (2+1)n &\small +2^2-6=1\\
\small \Leftrightarrow \space &\small 3n-2 = 1\\
\small ∴ \space &\small \displaystyle n = 1\\
\end{split}
よって、\(\small n\)も自然数となることから\(\small (m,n) = (2,1)\)と求まる。
\(\small m\)は3次方程式の自然数解だったので、自然数解は\(\small x=2\)…【答】.
他の2解については、\(\small n=1\)を問題の3次方程式に代入して求めればよい。
\begin{split}
&\small x^3+x^2-5x-2=0\\
\small \Leftrightarrow \space &\small (x-2)(x^2+3x+1)=0\\
\small ∴ \space &\small \displaystyle x=2, \space \frac{-3\pm\sqrt{5}}{2}\\
\end{split}
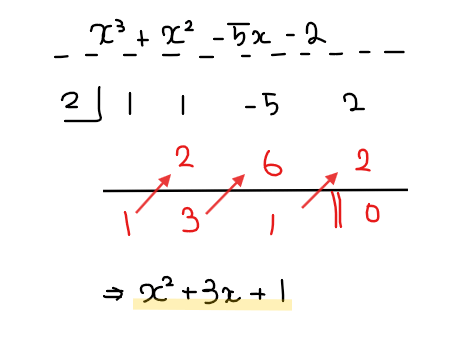
よって、他の2解は \(\small \displaystyle x=\frac{-3\pm\sqrt{5}}{2}\)…【答】.
本記事のまとめ
今回は3次方程式に関する問題として、1の3乗根(ω)の性質を利用した式の値や実数解・虚数解の性質や解の条件などから方程式の係数を決定する問題について解説しました。
今回解説した問題はどれも大学入試でも実際に出題されている典型問題なので、しっかりと復習して解き方の流れや考え方を頭に入れておきましょう!
最後に今回扱った問題を解く際のポイントだけおさらいしておきましょう。
☆重要Point☆
●1の3乗根を利用した式の値
・\(\small \omega^n\)を含む式の値は、\(\small \omega^3 =1\)、\(\small \omega^2+\omega+1 =0\)を利用して次数下げする。
●3次方程式の解の条件による係数決定
・実数解・虚数解など既知の解がある場合は因数を特定して因数分解する解法がおすすめ。
*虚数解は共役な複素数から解と係数の関係で2次方程式(因数)が求まる
・『3次方程式を、解から求めた因数で割り算した余りが0』の条件から係数決定する。
・重解や自然数解を持つ条件などは画一的な解き方はないものの、基本的には最低次数の文字で整理して因数分解することで糸口を掴む。
今回は以上です。お疲れさまでした!








コメント