【数Ⅲ_微分】微分可能とは？連続性や微分係数との関係性を理解するための最速ガイド

今回は微分可能とは何かについて徹底解説していきます。微分の定義に関する分野のため、微分係数や連続性など小難しい用語も多く、概念を理解するのが大変です。また、『微分可能であることを確認せよ』といった問題が中心になるため、高い論証力が求められることから難関大学入試でも出題される分野です。

そこで本記事では、微分可能性とは何なのかはもちろん、各種用語の意味や論証のポイントなどを感覚的に理解できるようなイメージ図も交えながら問題を通して完全ガイドしていきますので、是非最後まで一緒に頑張っていきましょう！

• 微分可能性をはじめて学ぶ人、基礎理解を深めたい人
• 微分可能性と連続性、微分係数の関係を理解したい人
• 微分可能性や連続性に関する問題を通して実践的な力をアップさせたい人
• 大学入試対策、定期テスト対策がしたい人

【問題＆解説】微分係数・微分可能性・連続性の問題

【問題1】微分可能性・連続性の確認（難易度：★★☆）

【感覚で理解】微分可能ってどういうこと？
端的に言うと、関数が微分可能とは、滑らかな曲線であることを表します。では、関数 \(\small f(x)\)が
\begin{split}
&\small \color{#ef5350}{\lim_{x \to a+0}\frac{f(x)-f(a)}{x-a}=\lim_{x \to a-0}\frac{f(x)-f(a)}{x-a}} \\
&\small \quad \cdots (*)\\
\end{split}
の条件を満たすとなぜ滑らかな曲線ということになるのかを解説していきます。そのためには、微分係数の定義と\(\small x \to a \color{red}{\pm 0}\)の意味を思い出す必要があります。

まず、微分係数とは
\begin{split}
\small f^\prime (a) = \lim_{x \to a}\frac{f(x)-f(a)}{x-a}
\end{split}
で定義されており、\(\small (*)\)の両辺と見比べるとほぼ同じ形をしています。そして、微分係数は図形的には接線の傾きを表しています（忘れちゃった人は「【数Ⅱ微分】接線・法線の方程式の求め方と典型問題（共通接線、曲線上にない点を通る接線）を徹底解説」の記事を確認しよう！）

次に、\(\small x \to a \color{red}{\pm 0}\)の意味について復習します。『\(\small \color{#ef5350}{x \to a \color{red}{\mathbf{+0}}}\)』は、\(\small x \ =a\)よりちょっと右側の値に限りなく近づけることをと表し、右側極限と呼びます。逆に、『\(\small \color{#5c6bc0}{x \to a \color{blue}{\mathbf{-0}}}\)』は、\(\small x \ =a\)よりちょっと左側の値に限りなく近づけることをと表し、左側極限と呼びます。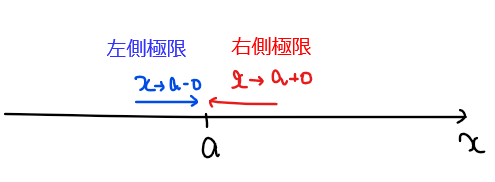


この知識を用いると、\(\small (*)\)の条件式は『\(\small x=a\)のちょっと左側での接線の傾きと、ちょっと右側での接線の傾きが同じ』のように日本語化できます。滑らかな曲線を思い浮かべると確かに\(\small x\)座標の位置によって接線の傾きが徐々に変わっていくので近くの点同士では接線の傾きは同じになることは感覚的にも理解できますね。これが微分可能という意味になります。逆に、カクカク折れ曲がるような関数では急に接線の傾きが変わってしまうので、微分可能ではないということになります。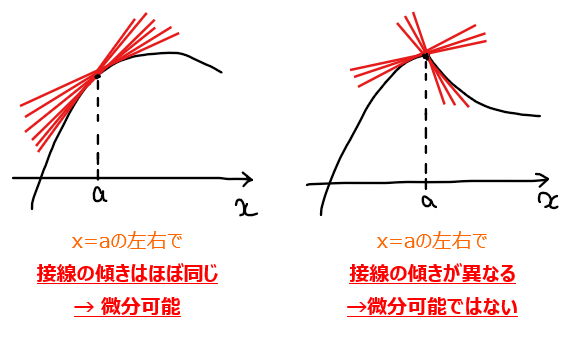


\(\small (*)\)のように右側極限をとった微分係数と左側極限をとった微分係数が等しくなるとき、単純に微分係数を
$$\small f^\prime (a) = \lim_{x \to a}\frac{f(x)-f(a)}{x-a}$$
とかき、微分可能といいます。

関数の連続性については、「【数Ⅲ_極限】関数の連続性とは？右側極限・左側極限を用いた問題の解き方・考え方を完全攻略！」で詳細を解説しています！

まず、\(\small x=0\)における関数の連続性について確認する。

\(\small f(x)\)の右側極限は、

\begin{split}
\small \lim_{x \to \color{red}{+0}} f(x)=\lim_{x \to +0} \frac{x}{1+3^\frac{1}{x}}
\end{split}

ここで、

\begin{split}
\small \lim_{x \to \color{red}{+0}} \frac{1}{x}=+\infty \space [*1]
\end{split}

*1：【補足】\(\small 1/x\)の右側極限
右側極限 \(\small x \to +0\)は、\(\small x=0\)の右側（正の方向）から徐々に\(\small x=0\)に近づけたときの\(\small \displaystyle \frac{1}{x}\)の値なので、下図のように\(\small + \infty\)となる。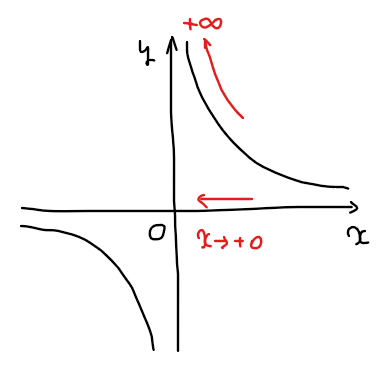

より、

\begin{split}
&\small \lim_{x \to \color{red}{+0}} (1+3^\frac{1}{x})\\
&\small = 1+3^\infty\\
&\small = \infty\\
\end{split}

よって、

\begin{split}
&\small \lim_{x \to +0} \frac{x}{1+3^\frac{1}{x}}\\
&\small =\frac{0}{\infty}\\
&\small =0 \space \cdots ①\\
\end{split}

一方で、\(\small f(x)\)の左側極限は、

\begin{split}
\small \lim_{x \to \color{blue}{-0}} f(x)=\lim_{x \to -0} \frac{x}{1+3^\frac{1}{x}}
\end{split}

ここで、

\begin{split}
\small \lim_{x \to \color{blue}{-0}} \frac{1}{x}=-\infty \space [*2]
\end{split}

*2：【補足】\(\small 1/x\)の左側極限
左側極限 \(\small x \to -0\)は、\(\small x=0\)の左側（負の方向）から徐々に\(\small x=0\)に近づけたときの\(\small \displaystyle \frac{1}{x}\)の値なので、下図のように\(\small -\infty\)となる。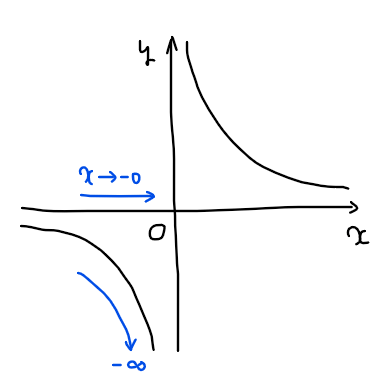

より、

\begin{split}
&\small \lim_{x \to \color{blue}{-0}} (1+3^\frac{1}{x})\\
&\small = 1+3^{-\infty}\\
&\small = 1+\frac{1}{3^{\infty}}\\
&\small = 1+0\\
&\small = 1\\
\end{split}

よって、

\begin{split}
&\small \lim_{x \to -0} \frac{x}{1+3^\frac{1}{x}}\\
&\small =\frac{0}{1}\\
&\small =0 \space \cdots ②\\
\end{split}

最後に、\(\small f(0)\)の値は関数の定義より\(\small f(0)=0\)…③であることから、①、②、③より

\begin{split}
&\small \lim_{x \to +0} f(x)=\lim_{x \to -0} f(x)=f(0)=0
\end{split}

となるので、関数\(\small f(x)\)は\(\small x=0\)で連続。

次に、\(\small x=0\)における微分可能性について確認する。

右側極限の微分係数は

\begin{split}
&\small \lim_{x \to +0}\frac{f(x)-f(0)}{x-0}\\
&\small = \lim_{x \to +0}\frac{f(x)}{x} \quad \color{magenta}{(∵ \space f(0)=0)}\\
\end{split}

ここで、今は右側極限（\(\small x=0\)のちょっと右側（＝正のほう））を考えているので、\(\small \displaystyle \frac{f(x)}{x}\)に代入する\(\small x\)の値としては \(\small 0<x\)と考えても問題ない。

ゆえに、関数 \(\small \displaystyle f(x)= \frac{x}{1+3^\frac{1}{x}}\)となるので

\begin{split}
&\small \lim_{x \to +0}\frac{f(x)}{x}\\
&\small = \lim_{x \to +0} \frac{1}{x}\cdot \frac{x}{1+3^\frac{1}{x}}\\
&\small = \lim_{x \to +0}\frac{1}{1+3^\frac{1}{x}}\\
&\small = \frac{1}{1+3^{\infty}} \quad \color{magenta}{◀ [*1]の利用}\\
&\small = \frac{1}{\infty}\\
&\small = 0 \quad \cdots ③\\
\end{split}

一方で、左側極限の微分係数は、\(\small x=0\)のちょっと左側（＝負のほう））の範囲で考えるため\(\small x<0\)となる点にだけ注意すれば、他は同様に計算すれば求めることができる。

\begin{split}
&\small \lim_{x \to -0}\frac{f(x)-f(0)}{x-0}\\
&\small = \lim_{x \to -0}\frac{f(x)}{x}\\
&\small = \lim_{x \to -0} \frac{1}{x}\cdot \frac{x}{1+3^\frac{1}{x}}\\
&\small = \lim_{x \to -0}\frac{1}{1+3^\frac{1}{x}}\\
&\small = \frac{1}{1+3^{-\infty}} \quad \color{magenta}{◀ [*2]の利用}\\
&\small = \frac{1}{1+0}\\
&\small = 1 \quad \cdots ④\\
\end{split}

よって、③、④より、

$$\small \lim_{x \to +0}\frac{f(x)-f(0)}{x-0} \neq \lim_{x \to -0}\frac{f(x)-f(0)}{x-0}$$

すなわち、右側極限の微分係数(=0)と左側極限の微分係数(=1)が一致しないことから、関数\(\small f(x)\)は\(\small x=0\)において微分可能ではない。

以上をまとめると、関数\(\small f(x)\)は\(\small x=0\)において連続であるが微分可能ではない…【答】.

【問題2】微分可能な関数の係数決定（難易度：★★☆）

【感覚で理解】なぜ微分可能であれば連続なのか？
微分可能とは、図形的には滑らかな曲線ということを説明しました。そして、連続とはつながっていることでした。ということは、『微分可能であれば連続』という主張は、図形的には『滑らかな曲線であれば線がつながっている（途切れることはない）』と言い換えることができます。そう言われるとその通りですね。このように図形的な意味合いに置き換えて考えてあげると、感覚的にも理解できた気になれます。

では逆に、『連続であれば微分可能』という主張は成り立つでしょうか？同様に図形的な解釈に置き換えて考えると、『線がつながっているならば滑らかな曲線である』となりますが、これは明らかに偽です。反例は無数にありますが、例えば下図ように途中で折れ曲がっている曲線は連続（途切れてはいない）ですが微分可能（滑らか）ではないですね。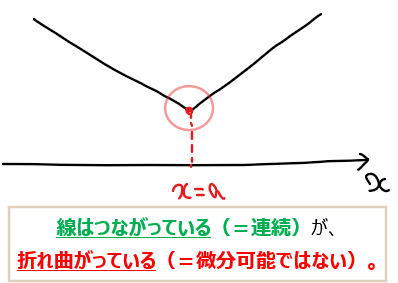

問題文から \(\small x>0\)の範囲では \(\small \displaystyle f(x)=\frac{1+3x-a\cos2x}{4x}\)、\(\small x≦0\)の範囲では、\(\small f(x)=bx+c\)なので、\(\small x \to +0\)や\(\small x \to -0\)での\(\small x\)の値によって利用する関数を間違えないようにはじめに関係を整理しておくとよい。

関数\(\small f(x)\)が\(\small x=0\)で微分可能であるとき、関数\(\small f(x)\)は\(\small x=0\)で連続でもあるので、

\begin{split}
\small \color{#ef5350}{\lim_{x \to +0}f(x) =\lim_{x \to -0}f(x)=f(0)}\\
\end{split}

を満たす。

\begin{split}
\small \lim_{x \to +0}f(x) &\small =\lim_{x \to +0}\frac{1+3x-a\cos2x}{4x}\\
\small \lim_{x \to -0}f(x) &\small =\lim_{x \to -0}(bx+c)=c\\
\small f(0) &\small = bx+c \space \big|_{x=0} =c\\
\end{split}

より、

\begin{split}
\small \lim_{x \to +0}\frac{1+3x-a\cos2x}{4x}=c \quad \cdots ①\\
\end{split}

①の左辺は\(\small x \to +0\)のとき分母が0になる一方で、右辺は実数 \(\small c\)に収束していることから、左辺が収束するためには分子も\(\small x \to +0\)の極限で0になる必要がある。

●OnePont：収束条件と不定形
極限値を持つ条件式の定数決定問題では『分母が0だから分子も0にならないと極限値を持てない』という論証をよく使います。仮に\(\small x \to +0\)で分母が0、分子が0以外の有限の値の場合 \(\small \displaystyle \left|\frac{有限値}{0}\right|=\infty\)に発散してしまいます（分子が無限大でも当然発散する）。そのため、不定形（式変形すれば有限の値になる可能性がある形）となることが必須条件になるわけです。
不定形のパターンについては「【関数の極限】不定形の全7パーンを分かりやすく解説（分数、ルート、三角関数などのn→∞、0の極限値）」で詳しく解説しているので、気になる人は確認してみてください！

よって、

\begin{split}
&\small \lim_{x \to +0}(1+3x-a\cos2x)=0\\
&\small \Leftrightarrow \space 1+0-a=0\\
&\small ∴ \space \color{#ef5350}{a=1 \space \cdots ②}\\
\end{split}

②を①に代入すると

\begin{split}
&\small \lim_{x \to +0}\frac{1+3x-\cos2x}{4x}=c\\
\small \Leftrightarrow \space &\small \lim_{x \to +0}\left(\frac{3}{4}+\frac{1-\cos2x}{4x}\right)=c\\
\small \Leftrightarrow \space &\small \frac{3}{4}+\lim_{x \to +0}\frac{(1-\cos2x)\color{#ef5350}{(1+\cos2x)}}{4x\color{#ef5350}{(1+\cos2x)}}=c\\
\small \Leftrightarrow \space &\small \frac{3}{4}+\lim_{x \to +0}\frac{1-\cos^2 2x}{4x(1+\cos2x)}=c\\
\small \Leftrightarrow \space &\small \frac{3}{4}+\lim_{x \to +0}\frac{\sin^2 2x}{4x(1+\cos2x)}=c\\
\small \Leftrightarrow \space &\small \frac{3}{4}+\frac{1}{4}\lim_{x \to +0}\left[\color{#ef5350}{\frac{\sin2x}{2x}}\cdot 2 \cdot \frac{\sin 2x}{(1+\cos2x)}\right]=c\\
\small \Leftrightarrow \space &\small \frac{3}{4}+\frac{1}{4}\cdot \color{#ef5350}1\cdot 2 \cdot \frac{0}{1+1}=c\\
\small \Leftrightarrow \space &\small \color{#ef5350}{c=\frac{3}{4}\space \cdots ③}\\
\end{split}

最後に\(\small x=0\)で微分可能である条件から

\begin{split}
\small \color{#ef5350}{\lim_{x \to +0}\frac{f(x)-f(0)}{x-0}=\lim_{x \to -0}\frac{f(x)-f(0)}{x-0} \space \cdots ④}
\end{split}

が成り立つ。あとは両辺をそれぞれ計算していけばよいだろう。

左辺について、\(\small x \to +0\)より、\(\small x>0\)と考えてよいので関数 \(\small \displaystyle f(x)=\frac{1+3x-\cos2x}{4x}\)であることと、\(\small f(0)\)の値は、\(\small x=0\)のときは関数の定義から \(\small \displaystyle f(x)=bx+\frac{3}{4}\)が適用されるため、\(\small \displaystyle f(0)=\frac{3}{4}\)であることに注意すると、

\begin{split}
&\small \displaystyle \lim_{x \to +0}\dfrac{\dfrac{1+3x-\cos2x}{4x}-\dfrac{3}{4}}{x}\\
&\small \displaystyle =\lim_{x \to +0}\dfrac{\dfrac{3}{4}+\dfrac{1-\cos2x}{4x}-\dfrac{3}{4}}{x}\\
&\small \displaystyle =\lim_{x \to +0}\frac{1-\cos2x}{4x^2}\\
&\small \displaystyle =\frac{1}{4}\lim_{x \to +0}\frac{1-\cos^2 2x}{x^2(1+\cos 2x)}\\
&\small \displaystyle =\frac{1}{4}\lim_{x \to +0}\left[\left(2\cdot \frac{\sin 2x}{2x}\right)^2\cdot \frac{1}{1+\cos 2x}\right]\\
&\small \displaystyle =\frac{1}{4}\left[\left(2\cdot 1\right)^2\cdot \frac{1}{1+1}\right]\\
&\small \displaystyle =\frac{1}{2} \space \cdots ⑤\\
\end{split}

一方、右辺は \(\small x \to -0\)より、\(\small x<0\)と考えてよいので関数の定義から \(\small \displaystyle f(x)=bx+\frac{3}{4}\)であることと、\(\small \displaystyle f(0)=\frac{3}{4}\)は変わらないことから、

\begin{split}
&\small \displaystyle \lim_{x \to -0}\dfrac{\left(bx+\dfrac{3}{4}\right)-\dfrac{3}{4}}{x}\\
&\small \displaystyle =b \space \cdots ⑥\\
\end{split}

④より、⑤、⑥が等しくなることから、\(\small \displaystyle b=\frac{1}{2} \space \cdots ⑦\).

以上、②、③、⑦より定数の値は、\(\small \displaystyle a=1,\space b=\frac{1}{2},\space c=\frac{3}{4}\)…【答】.

本記事のまとめ

今回は微分可能性の意味と微分可能となる条件について解説していきました。数式で考えると難しく感じる論証も図形的な解釈に置き換えて考えることで何を示すべきかが感覚的に理解でき、論証がしやすくなります。

最後に本記事のポイントを復習して終わりにしましょう。

☆重要ポイント☆
≪微分可能とは？≫
・図形的には、滑らかな曲線ということ。
・『左側極限の微分係数＝右側極限の微分係数』が成り立つ
　数式で書くなら
$$\small \displaystyle \lim_{x \to a+0}\frac{f(x)-f(a)}{x-a}=\lim_{x \to a-0}\frac{f(x)-f(a)}{x-a}$$
・微分可能なら連続（ただし、逆は成り立つとは限らない）。

≪連続とは？≫
・図形的には、曲線がつながっているということ。
・『\(\small y\)座標の値＝左側極限＝右側極限』が成り立つ
　数式で書くなら
$$\small \displaystyle f(a)=\lim_{x \to a+0}f(x) =\lim_{x \to a-0}f(x)$$

今回はここまでです。お疲れさまでした！