今回は2次方程式の解と係数の関係を利用した問題の中で、解の符号や解と実数の大小関係に関する問題について解説していきます。具体的には、2次方程式の解が異なる2つの正の解を持つ条件や異符号となる条件、あるいはある実数より大きい解と小さい解を持つ条件といったように、解に関する条件を満たすような2次方程式を求める問題の解き方や考え方のコツについて、分かりやすく解説していきます。
それでは早速確認していきましょう!
- 解と係数の関係を利用した解の符号・解と実数の大小関係の問題の解き方や問題を解くときの考え方(思考法)を理解したい人
- 異なる2つの正の解/負の解、異符号の解といった条件を数式化するコツを知りたい人
- 定期テスト対策、大学受験対策がしたい人
【問題&解説】解の条件を満たす2次方程式の求め方(解と係数の関係の利用)
【問題1】解の符号の条件(難易度:★★☆)
2次方程式 \(\small x^2-2px-p+2=0\)が次の条件を満たすような定数\(\small p\)の値の範囲を求めよ。
(1)異なる2つの正の解を持つ
(2)負の解を持つ
(3)異符号の解を持つ
・着眼点①:解の個数
*判別式の利用
・着眼点②:2数の和の符号
*互いに正(負):和の符号も正(負)
*互いに異符号 :符号の条件なし
・着眼点③:2数の積の符号
*互いに正(負):積の符号は正
*互いに異符号 :積の符号は負
●補足
着眼点②、③にある2数の和と積の符号の組合せを考えることで、2数がともに正なのかともに負なのか互いに異符号なのかいずれの組合せなのかを一意に判別することができる。詳しくは、2数の和と積に関する同値条件で解説する。
問題解決のKeyに記載の着眼点に注目して確認していく。
まず、解の個数については、問題文中に【異なる2つの】とあることから2個であることが分かる。解の個数に関する条件については、判別式の符号を確認すればよい。
よって、異なる2つの実数解を持つ条件は、
\begin{split}
\small \displaystyle \frac{D}{4} =&\small p^2-1\cdot(-p+2)>0\\
\small \Leftrightarrow \space &\small p^2+p-2>0\\
\small \Leftrightarrow \space &\small (p+2)(p-1)>0\\
\small ∴\space &\small \color{#ef5350}{p<-2, \space 1<p \space \cdots ①}\\
\end{split}
次に、2数の和の符号に着目する。本問では解の条件に【2つの正の解】とあることから、『2数=2つの異なる正の解』と考えて正の解の和の符号が満たす条件について考える。
ここで、問題の2次方程式の2つの解を\(\small \alpha , \space \beta\)とおくと、題意より2つの解\(\small \alpha , \space \beta\)は、\(\small \alpha >0\)かつ \(\small \beta>0\)を満たすことから、正の解の和も正、すなわち、\(\small \alpha +\beta >0\)を満たす。\(\small \alpha +\beta\)については、解と係数の関係より、\(\small \alpha +\beta =2p\)なので、
\begin{split}
&\small \alpha +\beta >0\\
\small \Leftrightarrow \space &\small 2p>0\\
\small ∴\space &\small \color{#ef5350}{p>0 \space \cdots ②}\\
\end{split}
最後に、2数の積の符号に着目する。これも和と同様に2つの正の解の積の符号が満たす条件を考えればよく、『正×正=正』なので、\(\small \alpha \beta >0\)を満たす。よって、解と係数の関係より、\(\small \alpha\beta =-p+2\)なので、
\begin{split}
&\small \alpha\beta >0\\
\small \Leftrightarrow \space &\small -p+2>0\\
\small ∴\space &\small \color{#ef5350}{p<2 \space \cdots ③}\\
\end{split}
以上から、①~③の共通範囲[*1]が求める範囲でなので、\(\small 1<p<2 \space \cdots\)【答】.
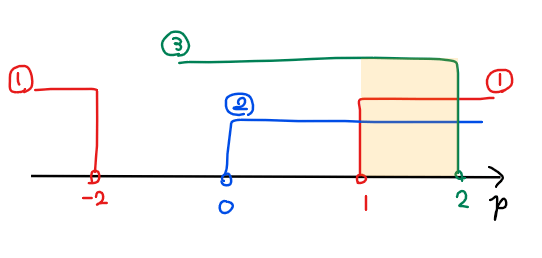
*1:【補足】共通範囲を考える理由
着眼点①~③の条件をすべて満たす解が今回求める解(異なる2つの正の解を持つ条件)なので、それぞれで得られた不等式の条件をすべて満たす範囲が求める範囲になる。よって、共通範囲を求めればよい。
解き方の流れは(1)と同様になる。
まず、解の個数についてだが、今回は「異なる2つの」という文言がなくただ単に「負の解を持つ」ことだけに言及されていることから、解の個数は1個以上あればOKである点に注意する。
よって、判別式が満たすべき条件は、\(\small D/4≧0\)より、
\begin{split}
\small \displaystyle \frac{D}{4} =&\small p^2-1\cdot(-p+2)≧0\\
\small \Leftrightarrow \space &\small p^2+p-2≧0\\
\small \Leftrightarrow \space &\small (p+2)(p-1)≧0\\
\small ∴\space &\small \color{#ef5350}{p≦-2, \space 1≦p \space \cdots ①}\\
\end{split}
次に、2数の和の符号に着目する。2次方程式の解を\(\small \alpha, \space \beta\)とおく(重解の場合は\(\small \alpha =\beta\)と考える)と、本問は負の解 \(\small \alpha <0\)かつ \(\small \beta<0\)を持つことが条件であり負の解の和は負になるため、\(\small \alpha +\beta<0\)を満たす。解と係数の関係より、\(\small \alpha +\beta =2p\)なので、
\begin{split}
&\small \alpha +\beta <0\\
\small \Leftrightarrow \space &\small 2p<0\\
\small ∴\space &\small \color{#ef5350}{p<0 \space \cdots ②}\\
\end{split}
最後に、2数の積の符号に着目すると、負の解の積は正(負×負=正)、すなわち\(\small \alpha \beta >0\)を満たすことから、解と係数の関係より、
\begin{split}
&\small \alpha\beta >0\\
\small \Leftrightarrow \space &\small -p+2>0\\
\small ∴\space &\small \color{#ef5350}{p<2 \space \cdots ③}\\
\end{split}
以上から、①~③の共通範囲が求める範囲でなので、\(\small p≦-2 \space \cdots\)【答】.
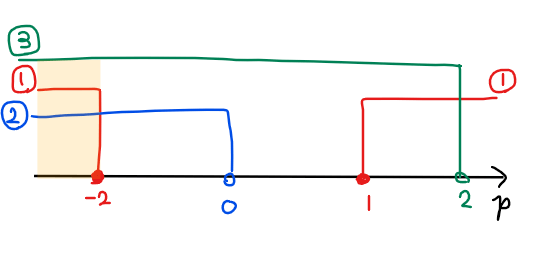
異符号の解を持つためには、2つの解を持つことが前提となるため、判別式が満たすべき条件は、\(\small D/4>0\)。この結果は、(1)の①となるため、\(\small \color{#ef5350}{p<-2, \space 1<p \space \cdots ①}\)。
2次方程式の2つの解を\(\small \alpha, \space \beta\)とおくと、異符号の解の和が満たすべき符号に関する条件は特になし[*1]。
*1:【補足】異符号の解の和の符号
たとえば、1つの解が-1で他方の解が3であれば、2解の和は\(\small -1+3=2>0\)となり、1つの解が3で他方の解が-5であれば、2解の和は\(\small 3+(-5)=-2<0\)のように異符号の足し算の結果は正にも負にもなり得るため、符号に関する条件はない。
最後に、異符号の解の積が満たすべき符号の条件について考えると、\(\small \alpha, \space \beta\)のどちらが正でどちらが負かに依らずに互いに異符号であることから、それらの積は負(正×負=負×正=負)になる。
よって、解と係数の関係より、
\begin{split}
&\small \alpha\beta <0\\
\small \Leftrightarrow \space &\small -p+2<0\\
\small ∴\space &\small \color{#ef5350}{p>2 \space \cdots ②}\\
\end{split}
よって、①、②の共通範囲が求める範囲なので、\(\small p>2 \space \cdots\)【答】.
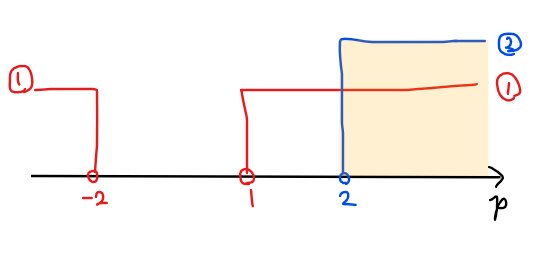
【問題2】解と実数の大小の条件(難易度:★★☆)
2次方程式 \(\small x^2+kx+k=0\)が次の条件を満たすような定数\(\small k\)の値の範囲を求めよ。
(1)2つの解がともに2以下の実数解を持つ
(2)1つの解が1より大きく、他方の解が1より小さい実数解を持つ
・2次方程式の解を\(\small \alpha ,\beta\)としたとき、(1)の解の条件は\(\small \alpha≦2\)かつ\(\small \beta ≦2\)となるが、この条件から和と積について
\begin{split}
&\small [\mathsf{和}]: \space\alpha+\beta≦4\\
&\small [\mathsf{積}]: \space \alpha\beta≦4\\
\end{split}
が成り立つというのは間違いなので注意!必ず同値条件が使える正(または負)の形に落とし込んでから和と積を考えること!
●同値条件とは?
条件Aと条件Bが数学的に同じ意味であるとき、AとBは同値条件であるという。
たとえば、\(\small x^2=1\)と\(\small x=\pm1\)は見た目は違う条件式だがどちらも\(\small x\)の値が1か-1という意味を表しているため、同値条件。一方で、\(\small x^2<1\)と\(\small x<1\)の条件は、たとえば\(\small x=-2\)を考えると、\(\small x<1\)の条件は満たすが、\(\small x^2<1\)は満たさない(代入すると\(\small 4<1\)となり不適)ため、同値条件ではない。
同値条件をうまく使いこなすことができれば、一見複雑な条件の問題であっても考えやすい条件式に置き換えて解くことができる。
※問題1の問題解決のKeyに記載した着眼点②、③を数式化したもの
[2数がともに正]
①:\(\small \alpha≧0\)かつ\(\small \beta ≧0\) ⇔ \(\small \alpha+\beta≧0\)かつ\(\small \alpha\beta ≧0\)
①’:\(\small \alpha>0\)かつ\(\small \beta >0\) ⇔ \(\small \alpha+\beta>0\)かつ\(\small \alpha\beta >0\)
[2数がともに負]
②:\(\small \alpha≦0\)かつ\(\small \beta ≦0\) ⇔ \(\small \alpha+\beta≦0\)かつ\(\small \alpha\beta ≧0\)
②’:\(\small \alpha<0\)かつ\(\small \beta <0\) ⇔ \(\small \alpha+\beta<0\)かつ\(\small \alpha\beta >0\)
[2数が異符号]
③:\(\small \alpha\)と\(\small \beta \)が異符号 ⇔ \(\small \alpha \beta <0\)
③’:\(\small \alpha\)と\(\small \beta \)の一方が0以下で他方が0以上 ⇔ \(\small \alpha \beta ≦0\)
数式だと分かりにくいかもしれないので補足すると、たとえば①は『2数が0以上であること』と『0以上の数同士の和や積が0以上であること』は同じ意味ということ。このことは以下のような図で考えると分かりやすい。
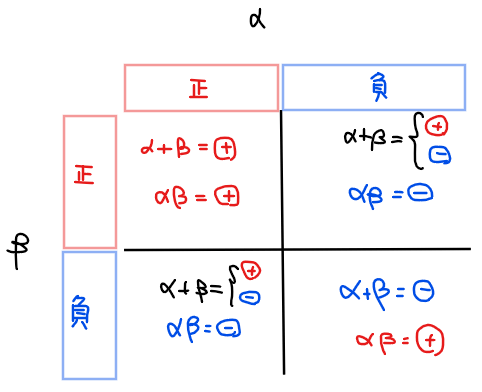
上図を見ると和と積の組合せから\(\small \alpha, \beta\)の符号が同符号(正or負)か異符号かを決定することができる。たとえば、和が負のパターンは左上以外の3パターンがあるが積が正という条件が加わることで右下のパターンと特定ができることから、\(\small \alpha <0, \beta <0\)と決定できる。他にも、積が負という条件があれば、\(\small \alpha ,\beta\)の2数が異符号(左下と右上)ということが特定できる。
この同値条件は図からも分かる通り符号の正負が判別のポイントになっているので、問題解決のKeyでも取り上げたように『0以外を基準とした場合』には適用できない点に注意が必要である。
●補足:『\(\small \alpha≦2\)かつ\(\small \beta ≦2\)』と『\(\small \alpha + \beta ≦4\)かつ\(\small \alpha\beta≦4\)』が同値条件ではない理由
一見すると成り立っていそうだが、よく考えてみるとたとえば\(\small \alpha =-5, \beta =-1\)の場合、『\(\small \alpha≦2\)かつ\(\small \beta ≦2\)』の条件は満たしているが、\(\small \alpha \beta =5\)となるため、2つ目の条件式『\(\small \alpha \beta ≦4\)』を満たすことができないため、同値条件ではないことになる(2以下の数の積は必ずしも4以下ではないということ)。
2次方程式の2つの解を \(\small \alpha , \space \beta\)とすると、『2つの解がともに2以下』という条件は、\(\small \alpha ≦2\)かつ \(\small \beta ≦2\)と数式化できる。
まず、解の個数に着目すると題意より、【2つの解】[*1]とあるので判別式が満たすべき条件は \(\small D≧0\)より、
\begin{split}
\small D =&\small k^2-4\cdot 1\cdot k≧0\\
\small \Leftrightarrow \space &\small k(k-4)≧0\\
\small ∴\space &\small \color{#ef5350}{k≦0, \space 4≦k \space \cdots ①}\\
\end{split}
*1:【補足】「2つの解」の解釈について
この手の問題でちょっと紛らわしい表現として「2つの解」がある。表現だけ見ると実数解が2個ある場合なので判別式の条件は\(\small D>0\)と思いたくなるが、これは誤り(・・;)。実は、2つの解には、異なる2つの解に加えて重解も含まれる(同じ解が2個あるとカウントされる)ため、判別式の条件は\(\small D≧0\)となることに注意されたい。
ちなみに、重解を含めない場合は、明示的に「異なる2つの解」という表現になる。
次に2数の和の符号に着目する。本問は問題1とは異なり、解の符号自体が正か負かは一概には言えない(2以下という条件なので、たとえば解が1とかであれば解の符号は正だが、-3とかであれば解の符号は負になる)。ここで、冒頭に数式化した解の条件 \(\small \alpha ≦2\)かつ \(\small \beta ≦2\)を少し変形して、
\begin{split}
&\small \alpha≦2 , \space \beta ≦2\\
\small \Leftrightarrow \space &\small \color{#ef5350}{\alpha-2≦0 , \space \beta-2 ≦0}\\
\end{split}
とすると、問題1の着眼点②の考え方を利用することができる。
\(\small \alpha -2\)と\(\small \beta -2\)は互いに0以下なので、『0以下』+『0以下』=0以下(0以下同士の和は0以下)になることから、
\begin{split}
&\small (\alpha-2)+(\beta-2) ≦0\\
&\small \Leftrightarrow \space \color{#ef5350}{\alpha +\beta}≦4\\
\end{split}
解と係数の関係より、\(\small \alpha +\beta =-k\)なので、与式より \(\small k≧-4 \space \cdots ②\) を得る。
最後に、2数の積の符号についても同様に \(\small \alpha -2\)と\(\small \beta-2\)の積を考えると、互いに0以下の数同士の積は0以上になることから、
\begin{split}
&\small (\alpha-2)(\beta-2)≧0\\
\small \Leftrightarrow \space &\small \color{#ef5350}{\alpha\beta}-2\color{#5c6bc0}{(\alpha+\beta)}+4≧0\\
\small \Leftrightarrow \space &\small \color{#ef5350}{k}-2\cdot \color{#5c6bc0}{(-k)}+4≧0 \quad \color{magenta}{◀解と係数の関係を利用}\\
\small \Leftrightarrow \space &\small 3k+4≧0 \\
\small \Leftrightarrow \space &\small \displaystyle \color{#ef5350}{k≧-\frac{4}{3} \space \cdots ③}\\
\end{split}
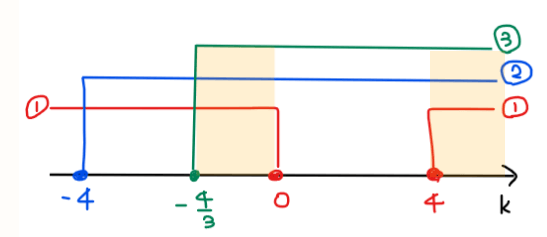
よって、①~③の共通範囲を求めると、\(\small \displaystyle -\frac{4}{3}≦k≦0, \space 4≦k\)…【答】.
2次方程式の2つの解を \(\small \alpha , \space \beta\)とすると、『1つの解が1より大きく、他方の解が1より小さい』という条件は、\(\small \alpha <1\)かつ \(\small 1< \beta \)と数式化できる。故に、2つの解は
\begin{split}
&\small \color{#ef5350}{\alpha -1 <0 ,\space \beta -1>0 \quad \cdots (*)}\\
\end{split}
を満たす。
解の個数は題意より2個の実数解を持つ必要がある(重解だと明らかに1より大きく1より小さい解という条件を満たせない)ので、
\begin{split}
\small D =&\small k^2-4\cdot 1\cdot k>0\\
\small \Leftrightarrow \space &\small k(k-4)>0\\
\small ∴\space &\small \color{#ef5350}{k<0, \space 4<k \space \cdots ①}\\
\end{split}
\(\small (*)\)の条件式は2数が異符号であることを表しているため、\(\small \alpha -1\)と\(\small \beta-1\)の和と積に関する同値条件より、『2数が異符号』 ⇔ 『2数の積が負』(積の符号の条件)が成り立つので
\begin{split}
&\small (\alpha-1)(\beta-1)<0\\
\small \Leftrightarrow \space &\small \alpha\beta-(\alpha+\beta)+1<0\\
\small \Leftrightarrow \space &\small k-(-k)+1<0\\
\small \Leftrightarrow \space &\small 2k+1<0\\
\small ∴\space &\small \displaystyle \color{#ef5350}{k<-\frac{1}{2} \space \cdots ②}\\
\end{split}
※和の符号に関しては特に条件はなし。
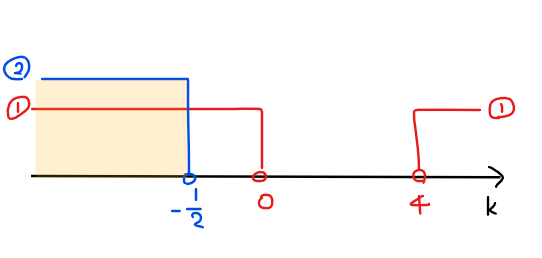
よって、①、②の共通範囲より、\(\small \displaystyle k<-\frac{1}{2} \space \cdots\)【答】.
●補足
実は2数の積が負という条件を課す場合2数が同じ値になることはないため、判別式>0(異なる解が2個)という条件は確認しなくても『積が負』の条件だけを考えればOKである。
【理解を深める】グラフを利用した別解
問題1、2での解説では今回は2次方程式の解と係数の関係を利用して解く方法について解説しましたが、解の条件を満たすような定数の範囲を求める問題のもう一つ重要な考え方としてグラフを利用した解法(いわゆる解の配置問題や解の存在範囲の問題)が挙げられます。
問題1、2で取り上げた問題については解の配置問題の考え方でも解くことができます。詳しい解法については、【解の配置問題】2次方程式の解の存在範囲(パターン別解法を徹底解説)の記事で解説しています。
2つの解法があると必ず聞かれるのが「どっちがおすすめ?」という質問です。この質問について、個人的な見解を述べておくと、解の配置問題の解法をおすすめします。理由は、解の配置問題で考えておけばどんな解の条件の問題でも大体解くことができるからです。
解と係数の関係の利用については、今回紹介したような「解の符号」や「解がある実数より大きい(小さい)」といった条件であれば解くことが可能ですが、「2つの解が0以上3以下になる」といった条件の場合、条件を数式化すると\(\small 0≦\alpha≦\beta≦3\)のようになりますが、ここからうまく\(\small \alpha +\beta\)や\(\small \alpha\beta\)の形を作り出すことができないため、解と係数の関係が利用できる形になりません。一方で、解の配置問題として解く場合は、常に『軸』、『判別式』、『境界条件』が満たすべき条件を考えればよいので、問題によって考え方を変えずに解くことができる点で汎用性が高い解法だと言えます。
本記事のまとめ
今回は解と係数の関係を利用した2次方程式の解の符号や解と実数の大小関係に関する問題について解説しました。解き方のコツとしては、解の個数、2数の和の符号、2数の積の符号の3つの着眼点を意識することで解くことができます。特に、和の符号と積の符号については、2数の和と積に関する同値条件を利用することで条件式を立式し、解と係数の関係を利用して不等式を解く流れになります。
一般的には解の配置問題でも解くことができますが、グラフを利用した条件式の立式は面倒なのに比べて解と係数を利用した解法は割と簡単なので、知っていれば時間短縮に役立ちます。また、複数の解法を知っていると検算時にも役立つので、どちらの方法でも解けるようにしておきましょう。
では今回は以上です。お疲れさまでした!






コメント