今回は、2次方程式の解の配置問題についてパターン別に解き方を徹底解説していきたいと思います。いきなりですが、皆さんは次の問題の答え分かりますか?
2次方程式、\(\small x^2-2ax+a+2=0\)が、\(\small -2 < x < 2 \)に少なくとも1つの実数解を持つとき、定数\(\small a\)の値の範囲を求めよ。
この問題のように、ある条件を満たすような方程式の解を求める問題を「解の配置問題」や「解の存在範囲」を求める問題と言ったりします。
本記事ではこのような問題の解き方について、考え方や解き方のコツを含めて解説しています(冒頭の問題もこのあとの記事で解説しています!)。苦手だなと思った人はぜひ最後まで読んで、一緒に苦手を克服していきましょう!
- 解の配置問題を解くときの考え方が知りたい!
- 解説を読んでもどの条件を使って解けばいいのかわからない…
- 問題のパターンごとの解き方が知りたい!
- 定期テスト/受験対策向けに解の配置を解けるようにしたい!
【基礎知識】2次方程式の解の配置問題の解き方
解の配置問題とは
解の配置問題とは、『方程式の解がどこにあるか?』という条件から定数の値の範囲などを求める問題です。解の存在範囲と呼ばれることもあります。
解き方の基本方針
2次方程式の解の配置問題を解くときには、3つの観点に着目して考えるとうまく解くことができます。
■2次方程式の解の配置問題の解き方
・STEP1:問題を満たす2次関数のグラフを図示
・STEP2:グラフをもとに3つの観点で条件を確認
- 判別式の条件
- 軸の範囲
- 境界での\(\small y\)座標
端的に言うと「グラフをかいて、条件を調べる」という非常にシンプルな手順になります。
3つの観点の3番目に書いた「境界での\(\small y\)座標」について少しわかりにくいと思うので補足します。
境界とは、ある条件を満たす範囲と満たさない範囲の境目(境界)のことです。たとえば、「正の実数解」と「負の実数解」を分けている境目は『\(\small x=0\) (\(\small y\) 軸)』です。この場合、\(\small x=0\)での\(\small y\)座標に着目するとうまく解くことができます。
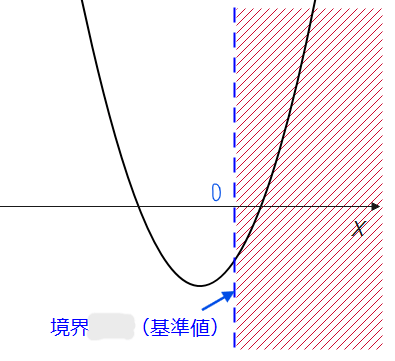
それぞれ解を持つという条件であれば、
正負を分ける\(\small x=0\)(青線部分)が境界。
2次方程式の解の配置問題を考える上では、『境界条件=基準値』と言い換えるとわかりやすいかもしれません。
問題の基本パターンと解法
解の配置問題は大きく次の3パターンに分類できます。
■解の配置問題の基本パターン
- パターン①:基準値以上/以下の実数解を持つ
- パターン②:ある区間内に実数解を持つ
- パターン③:基準値の左右に実数解を持つ
【パターン①】基準値以上/以下の実数解を持つ
基準値以上/以下の実数解を持つパターンです。
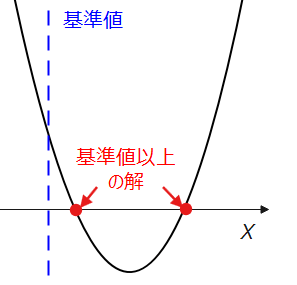
異なる2つの実数解を持つ
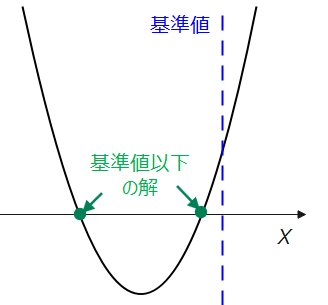
異なる2つの実数解を持つ
例えば、『基準値以上の異なる2つの実数解を持つ』場合の条件は、パターン①-1のようなグラフを描くことで、「判別式」、「軸の範囲」、「境界での\(\small y\)座標」は以下の通りになることが分かります。
■基準値以上の異なる2つの実数解を持つ場合
以下3つの条件の共通範囲を考えればOK。
・判別式:\(\small \color{red}{D>0}\)
・軸の範囲:「軸」\(\small \color{blue}>\) 基準値
・境界での\(\small y\)座標:「基準値での\(\small y\)座標」\(\small \color{red}{≧0}\) ※基準値が境界になる
逆に、『基準値以下の異なる2つの実数解を持つ』場合の条件は、パターン①-2のようなグラフをかくことで以下の通りになることが分かります。
■基準値以下の異なる2つの実数解を持つ場合
以下3つの条件の共通範囲を考えればOK。
・判別式:\(\small \color{red}{D>0}\)
・軸の範囲:「軸」\(\small \color{blue}<\) 基準値
・境界での\(\small y\)座標:「基準値での\(\small y\)座標」\(\small \color{red}{≧0}\) ※基準値が境界になる
【パターン②】ある区間内に実数解を持つ
たとえば、『\(\small a≦x≦b\)に実数解を1つだけ持つ』や『\(\small a≦x≦b\)に異なる2つの実数解を持つ』などが該当します。
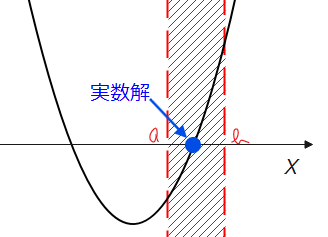
実数解を1つだけ持つ
異なる2つの実数解を持つ
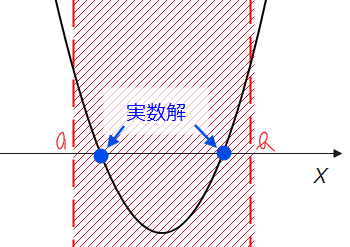
たとえば、『区間内 \(\small a≦x≦b\) に異なる2つの実数解を持つ』の場合であれば、パターン②-2のようなグラフを描くことで、「判別式」、「軸の範囲」、「境界条件」は以下の通りになることが分かります。
■区間内 \(\small a≦x≦b\) に異なる2つの実数解を持つ場合
以下3つの条件の共通範囲を考えればOK。
・判別式:\(\small \color{red}{D>0}\)
・軸の範囲:\(\small \color{red}{a<}\)「軸」\(\small \color{red}{<b}\)
・境界での\(\small y\)座標:「\(\small x=a\)での\(\small y\)座標」\(\small \color{red}{≧0}\)かつ
「\(\small x=b\)での\(\small y\)座標」\(\small \color{red}{≧0}\) ※区間の両端が境界になる
【注意】条件を満たすグラフに他のパターンがないか確認する
たとえば、『\(\small a≦x≦b\)に実数解を1つだけ持つ』を考えるときに、パターン②-1のようなグラフを思いついたとして、この図をもとにすると以下の条件がよさげですが、これは間違いです。
・判別式:\(\small \color{red}{D>0}\)
・軸の範囲:「軸」\(\small \color{red}{<a}\) ※間違い
・境界での\(\small y\)座標:「\(\small x=a\)での\(\small y\)座標」\(\small \color{red}{≦0}\)かつ ※間違い
「\(\small x=b\)での\(\small y\)座標」\(\small \color{red}{≧0}\) ※間違い
●間違いの理由①:パターン漏れ
下図のような場合でも条件を満たすので、「軸の範囲」と「境界での\(\small y\)座標」の条件は必ずしも成立しません。他のパターンがないかチェックしましょう。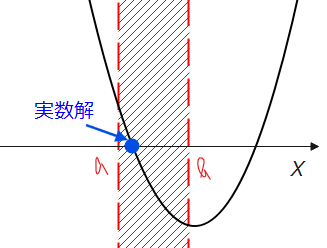
●間違いの理由②:条件が一般的ではない
パターン②-1のグラフだけを見て「「軸」\(\small <a\)」としていますが、実際には以下のような位置関係もあり得るので「特殊な場合になってないか?」、「本当に一般的な条件か?」をチェックするようにしましょう。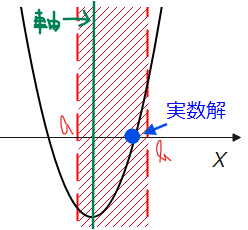
●考慮漏れを防ぐには…
経験によってある程度漏れを防ぐことができますが、個人的には次の2点を意識するのがよいかなと思っています。それが、「グラフを左から右へ動かしていき条件を満たすか確認する」と「条件の妥当性まで考える」です。
1つ目は、2次関数のグラフを左→右へ徐々に動かしていき、どこで条件を満たして、どこで条件を満たさないのかを確認することで、分岐点となるポイントの条件が見えてきます。
2つ目は少し上級者向けですが、図から条件を出したら、どうしてその条件になるのかという理由を考えてみるというものです。たとえば、『\(\small a≦x≦b\)に実数解を1つだけ持つ』問題の「境界での\(\small y\)座標」の条件は、グラフを動かして確認していくと「\(\small x=a\)での\(\small y\)座標と\(\small x=b\)での\(\small y\)座標の符号が異なる」ことだと分かります。これは、少し考えると1つだけ解を持つということは\(\small a~b\)の区間で\(\small x\)軸と2次関数が1回だけ交差するということなので、確かに交差の前後で\(\small y\)座標の符号が変わることが分かります。
【パターン③】基準値の左右に実数解を持つ
たとえば、『\(\small x=2\)以上の実数解を持つ』や、『正の実数解と負の実数解を持つ(=『\(\small x=0\)以上/以下の解を持つ』)』などのように、基準値の左側と右側でそれぞれ解を持つパターンです。この場合、図からもわかるように『基準値で\(\small y\)座標の値は必ず負』になります。
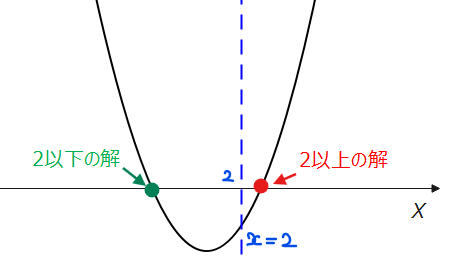
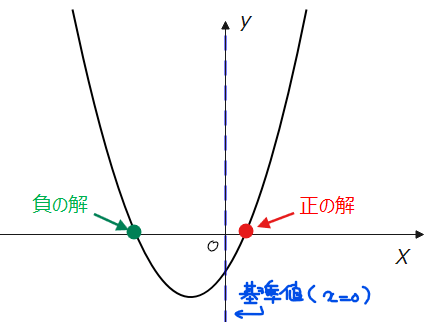
■基準値の左右に実数解を持つ場合
・境界での\(\small y\)座標:「基準値で\(\small y\)座標」\(\small \color{red}{<0}\)
※上記条件を満たせば「判別式」、「軸の範囲」の条件も
自動的に満たされるので考えなくてもOK
—以下の条件は考えなくてOK—
・判別式:\(\small \color{red}{D>0}\)
・軸の範囲:特になし
【問題&解説】2次方程式の解の配置問題
では、実際の問題を通してパターンごとの解き方を理解していきましょう!
【基本】問題1:基準値以上の実数解
2次方程式、\(\small x^2-2ax+a+2=0\)が1より大きい異なる2つの実数解を持つとき、定数\(\small a\)の値の範囲を求めよ。
今回の問題は「パターン①:基準値以上/以下の実数解を持つ」に該当します。
2次関数を\(\small f(x)=x^2-2ax+a+2\)とする。
\(\small f(x)\)は軸が\(\small x=a\)という点を踏まえ、問題の条件を満たす図を描くことで、「判別式の条件」、「軸の範囲」、「境界での\(\small y\)座標」を考える。
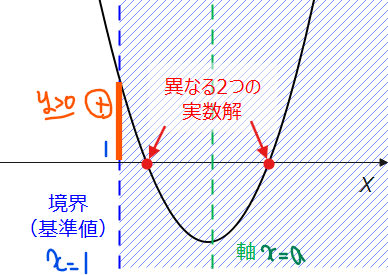
[1]判別式の条件
問題文に記載の通り「異なる2つの実数解」なので
\begin{split}
\frac{D}{4}=a^2-1\cdot(a+2)&\color{red}{>0}\\
a^2-a-2&>0\\
(a+1)(a-2)&>0\\
\Rightarrow \space \color{red}{a<-1、2<a}&\quad \color{red}{\cdots①}\\
\end{split}
[2]軸の範囲
図より、2つの解が1より大きな実数解となるためには、軸は\(\small x>1\)の範囲(青斜線範囲)にある必要がある(仮に軸が1以下にあると、軸より左側の解が必ず1より小さくなる)。
よって、軸が満たすべき範囲は、
$$a>1\quad \cdots②$$
[3]境界での\(\small y\)座標
境界は基準値となる\(\small x=1\)なので、\(\small x=1\)のときの\(\small y\)座標が正になっている必要があることから
\begin{split}
f(1)=1^2-&2\cdot a\cdot 1+a+2\color{red}{>0}\\
\Rightarrow \space -a&+3>0\\
&\color{blue}{a<3 \quad \cdots③}\\
\end{split}
最後に①~③の共通範囲をとれば答えになる。
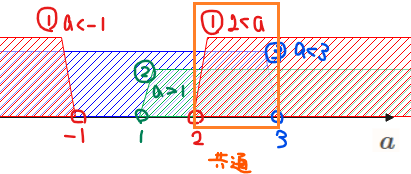
(補足)共通範囲を考える理由
[1]~[3]は、問題文にある「1より大きい異なる2つの実数解を持つ」という条件を数式化したものなので、どれか1つの条件でも満たさないものがあると完璧ではなくなってしまいます。そのため、すべてを満たす範囲、すなわち共通範囲を考える必要があるのです。
(解答)
\(\small \quad \color{red}{2<a<3}\)
【基本】問題2:ある区間内の実数解
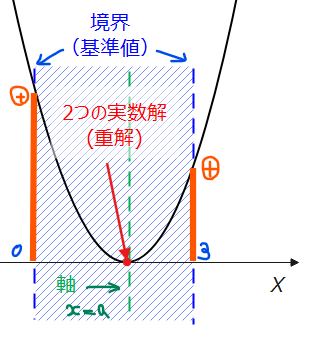
2次方程式、\(\small x^2-2ax+4=0\)において、2つの解がともに\(\small 0 < x < 3\)にあるとき、定数\(\small a\)の値の範囲を求めよ。
今回の問題は「パターン②:ある区間内に実数解を持つ」に該当します。パターンが変わっても解き方の方針は変わりません!
2次関数を\(\small f(x)=x^2-2ax+4\)とする。
\(\small f(x)\)は軸が\(\small x=a\)という点を踏まえ、問題の条件を満たす図を描くことで、「判別式の条件」、「軸の範囲」、「境界での\(\small y\)座標」を考える。
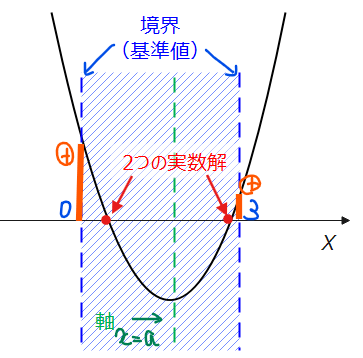
(補足)「2つの解」と「異なる2つの解」の違い
異なる2つの解は文字通り2つの解が存在していることを意味する一方で、2つの解は重解も含みます。「重解は1つの解でしょ?」と思った人も多いと思いますが、あくまで2つの解がたまたま同じ値になったというだけで解としては2つになります(ややこしいので注意が必要…)。
この説明は私自身納得してないのですが、ここは正直理解するというよりは、そういうものなんだと暗記しちゃった方がよいと思います。
[1]判別式の条件
問題文に記載の通り「2つの実数解」なので、重解の場合も含むことに注意して
\begin{split}
&\frac{D}{4}=a^2-4\color{red}{≧0}\\
\Rightarrow \space &\color{red}{a≦-2、2≦a}\quad \color{red}{\cdots①}\\
\end{split}
[2]軸の範囲
図より、2つの解が \(\small 0<x<3\)の範囲に存在するためには、軸も\(\small 0<x<3\)の範囲(青斜線範囲)に存在する必要があることから、
$$0<a<3\quad \cdots②$$
[3]境界での\(\small y\)座標
境界は解の存在範囲の端点となる \(\small x=0\) および \(\small x=3\) なので、\(\small x=0、3\)のそれぞれで\(\small y\)座標が正になっている必要があることから
\begin{split}
&
\begin{cases}
f(0)\color{red}{>0} \quad \mathbf{かつ} \\
f(3)\color{red}{>0}\\
\end{cases}\\
&\Rightarrow \space
\begin{cases}
f(0)=4\color{red}{>0} \space (\mathbf{これは当然に成り立つ関係式}) \quad \mathbf{かつ} \\
f(3)=3^2-2\cdot a\cdot 3+4\color{red}{>0}\\
\quad \Rightarrow \space -6a+13>0\\
\quad \Rightarrow \space \color{blue}{a<\dfrac{13}{6}\quad \cdots③}\\
\end{cases}
\end{split}
最後に①~③の共通範囲をとれば答えになる。
(解答)
\(\small \quad \displaystyle \color{red}{2≦a<\frac{13}{6}}\)
【基本】問題3:基準値の左右の実数解
2次方程式、\(\small x^2-ax+a^2-3a=0\)において、2より大きい実数解と2より小さい実数解を持つとき、定数\(\small a\)の値の範囲を求めよ。
今回の問題は「パターン③:基準値の左右に実数解を持つ」に該当します。
2次関数を\(\small f(x)=x^2-ax+a^2-3a\)とする。
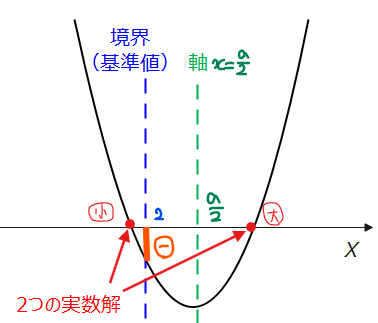
\(\small f(x)\)は軸が\(\small x=\dfrac{a}{2}\)という点を踏まえ、問題文の条件を満たすグラフを図示すると以下の通り。
[1]判別式の条件
問題文から、「異なる2つの実数解」を持つ必要があることから
\begin{split}
&D=a^2-4(a^2-3a)\color{red}{>0}\\
&a^2-4a^2+12a>0\\
&a(a-4)<0\\
\Rightarrow &\space \color{red}{0<a<4}\quad \color{red}{\cdots①}\\
\end{split}
[2]軸の範囲
軸の位置に関しては、以下の図のような場合でも問題の条件を満たすため、「この範囲にないといけない」という縛りはありません。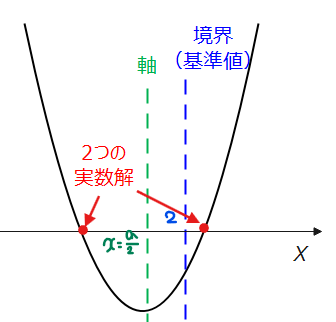
[3]境界での\(\small y\)座標
境界は基準値となっている \(\small x=2\) であり、\(\small x=2\)のとき\(\small y\)座標が負になっている必要があることから
\begin{split}
f(2)=&2^2-2a+a^2-3a<0\\
&a^2-5a+4<0\\
&(a-1)(a-4)<0\\
\Rightarrow &\space \color{blue}{1<a<4 \quad \cdots②}\\
\end{split}
以上①~②の共通範囲をとれば答えになる。
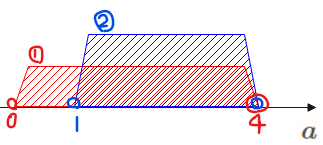
(補足)境界での\(\small y\)座標の条件だけ考えればよい?
「パターン③:基準値の左右に実数解を持つ」では、「境界での\(\small y\)座標\(\small <0\)」の条件を満たせば、他の「判別式」、「軸」の条件も自動的に満たすので、実は②の条件がそのまま解答になることは覚えておくとよいでしょう。
(解答)
\(\small \quad \displaystyle \color{red}{1<a<4}\)
【応用】問題1:ただ1つの実数解
2次方程式、\(\small x^2-2ax+a+2=0\)が次の条件を満たすような定数\(\small a\)の値の範囲を求めよ。
(1) 異なる2つの実数解のうち、ただ1つが \(\small -2 < x < 2\)にある。
(2) 異なる2つの実数解のうち、ただ1つが \(\small -2≦x≦2\)にある。
■ある区間に1つだけの解を持つ場合
区間の両端で解を持つパターンを考慮するべし!
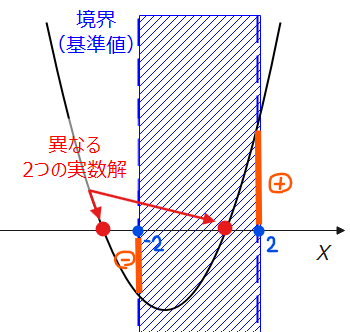
問題文の条件を満たすような解の配置は上図の通り。では、それぞれの条件について考えていこう。
[1]判別式の条件
問題文から、「異なる2つの実数解」を持つ必要があることから
\begin{split}
\frac{D}{4}&=a^2-(a+2)\color{red}{>0}\\
&(a-2)(a+1)>0\\
\Rightarrow &\space \color{red}{a<-1、2<a}\quad \color{red}{\cdots①}\\
\end{split}
[2]軸の範囲
軸の位置に関しては、軸がどんな位置にあっても問題の条件を満たすことがあるため、「この範囲にないといけない」という縛りはありません。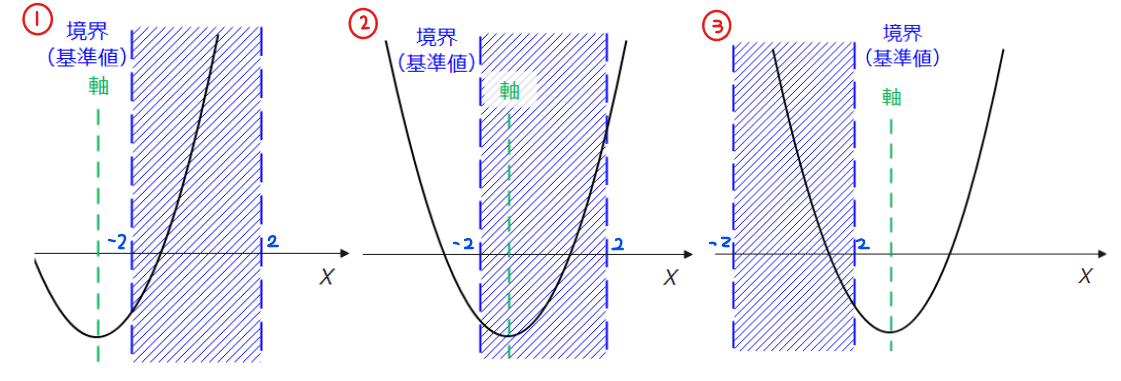
[3]境界での\(\small y\)座標
境界は基準値となっている \(\small x=-2、2\) であり、[2]にある図の①~③のパターンを見てもわかるように、「\(\small x=-2\)のとき\(\small y\)座標の符号」と「\(\small x=2\)のとき\(\small y\)座標の符号」が逆になっている必要があることから、\(\small f(x)=x^2-2ax+a+2\)とおくと、\(\small f(-2)f(2)<0\)(符号が逆ということはかけ算するとマイナスになる)となっていればOKです…パターン1。
一方で、今考えている区間\(\small -2<x<2\)は端点である\(\small x=\pm 2\)を含まないので、ちょうど端点に解を持つような場合でも問題の条件を満たすことがあることに注意します。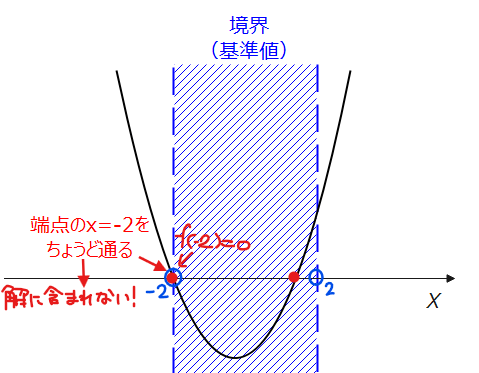
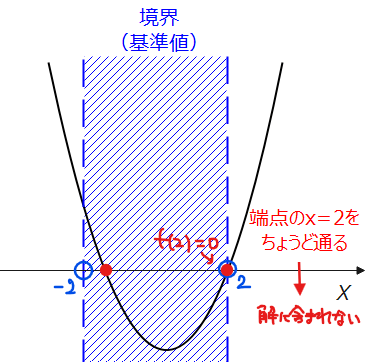
たとえば、\(\small x=-2\)で解を持つ場合(つまり\(\small \color{red}{f(-2)=0}\))は\(\small -2<x<2\)の区間には含まれないので、もしもう一つの解が\(\small -2<x<2\)の区間にあれば、\(\small -2<x<2\)を満たす解はただ1つになり条件を満たします…パターン2。
同様に、\(\small x=2\)でちょうど解を持ち(つまり\(\small \color{red}{f(2)=0}\))、\(\small -2<x<2\)の区間に解を持つ場合も問題の条件を満たします…パターン3。
\(\small -2<x<2\)の区間にただ1つの解を持つためには、以上の3パターンのいずれかを満たせばよいので、それぞれの条件のOR条件(合計範囲)を求めていきます。
■境界での\(\small y\)座標の場合分けパターン
・パターン1:境界の両端での符号が異なる・・・\(\small \color{red}{f(-2)f(2)<0}\)
・パターン2:境界の左端で解を持つ・・・\(\small \color{red}{f(-2)=0}\)
・パターン3:境界の右端で解を持つ・・・\(\small \color{red}{f(2)=0}\)
●パターン1:境界の両端で符号が異なる場合
\(\small \color{red}{f(-2)f(2)<0}\)を満たすので、
\begin{cases}
f(-2)=4+4a+a+2=\color{red}{5a+6}\\
f(2)=4-4a+a+2=\color{red}{-3a+6}\\
\end{cases}
より、
\begin{split}
&f(-2)f(2)<0\\
&(5a+6)(-3a+6)<0\\
&(5a+6)(a-2)>0\\
\Rightarrow &\space \color{blue}{a<-\frac{6}{5}、2<a \quad \cdots②}\\
\end{split}
●パターン2:\(\small f(-2)=0\)の場合
\begin{split}
&f(-2)=5a+6=\color{red}0\\
& \Rightarrow \space \color{red}{a=-\frac{6}{5}}\\
\end{split}
となるので、問題文の2次方程式 \(\small x^2-2ax+a+2=0\)に代入して整理すると、
\begin{split}
&5x^2+12x+4=0\\
&(5x+2)(x+2)=0\\
\Rightarrow &\space x=-2、-\frac{2}{5}\\
\end{split}
\(\small x=-2\)はもともと知っていた解で、もう一つの解が\(\small x=-\frac{2}{5}\)となるが、これは\(\small -2<x<2\)の区間の解であるため、条件を満たす。よって、\(\small \displaystyle \color{blue}{a=-\frac{6}{5}\cdots ③}\)は適切。
●パターン3:\(\small f(2)=0\)の場合
\begin{split}
&f(2)=-3a+6=\color{red}0\\
& \Rightarrow \space \color{red}{a=2}\\
\end{split}
となるので、問題文の2次方程式 \(\small x^2-2ax+a+2=0\)に代入して整理すると、
\begin{split}
&x^2-4x+4=0\\
&(x-2)^2=0\\
\Rightarrow &\space x=2\\
\end{split}
となるため、\(\small -2<x<2\)の区間の解を持たないことから不適。
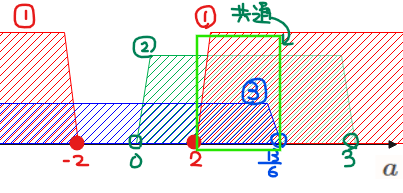
よって、パターン1~3のOR条件(合計範囲)は②、③の合計範囲になるため、
$$\color{blue}{a≦-\frac{6}{5}、2<a\cdots④}$$
最後に[1]~[3]の共通範囲([1]~[3]は全部満たさないと問題文の条件を満たせないので)を考えたもの、すなわち①と④の共通範囲が答えになる。
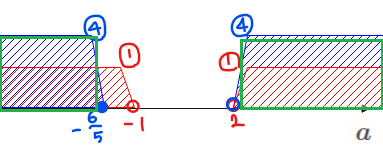
(解答(1))
\(\small \quad \displaystyle \color{red}{a≦-\frac{6}{5}、2<a}\)
(1)で求めた結果を利用する。(1)との違いは解の存在範囲が「\(\small \color{red}{-2≦x≦2}\)」となっており、区間の両端を含むということ。
判別式の条件と軸の範囲、境界での\(\small y\)座標の計算結果は(1)と同じため、ポイントに絞って解説する。
[1]判別式の条件
異なる2つの実数解という条件は変わらないため、結果は同じでOK。
\begin{split}
\color{red}{a<-1、2<a}\quad \color{red}{\cdots①}\\
\end{split}
[2]軸の範囲
考え方は変わらないので同じ結果でOK。
[3]境界での\(\small y\)座標
端点が含まれたことにより、パターン2、3の考え方に変化あり。
●パターン1:端点で符号が異なる場合
(1)と同じなので結果のみ記載。
\begin{split}
\color{blue}{a<-\frac{6}{5}、2<a \quad \cdots②}\\
\end{split}
●パターン2:\(\small f(-2)=0\)の場合
(1)の結果より、\(\small -2≦x≦2\)の区間に\(\small x=-2、-\frac{2}{5}\)の2つの解を持ってしまうため、ただ1つの解を持つという問題の条件と合わないため不適。
●パターン3:\(\small f(2)=0\)の場合
(1)の結果より、\(\small x=2\)の重解となり、問題の条件である異なる2つの実数解という条件に反するため不適。
[1]~[3]の共通範囲(つまり①、②の共通範囲)を求めたものが答えになる。
(解答(2))
\(\small \quad \displaystyle \color{red}{a<-\frac{6}{5}、2<a}\)
【応用】問題2:少なくとも1つの実数解
2次方程式、\(\small x^2-2ax+a+2=0\)が、\(\small -2 < x < 2 \)に少なくとも1つの実数解を持つとき、定数\(\small a\)の値の範囲を求めよ。
■少なくとも1つの実数解を持つ場合
「2つの実数解を持つ場合」と「1つの実数解を持つ場合」の2パターンに分けて考えろ!
■2つの実数解を持つ場合
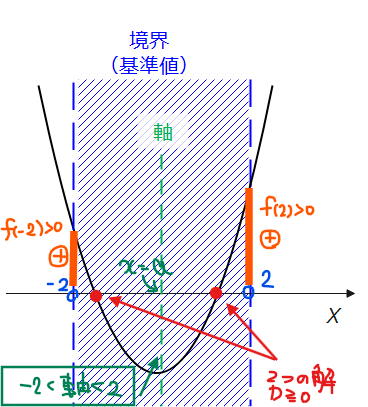
描いてみると、判別式、軸、境界の\(\small y\)座標に
上図のような特徴が見えてくる
[1]判別式の条件
「2つの実数解」(異なるとは言われてない)なので、重解でもOKであることに注意すると
\begin{split}
\frac{D}{4}=& a^2-(a+2) \color{red}{≧0}\\
&(a-2)(a+1)≧0\\
\Rightarrow \space & \color{red}{a≦-1、2≦a}\quad \color{red}{\cdots①}\\
\end{split}
[2]軸の範囲
\(\small f(x)=x^2-2ax+a+2\)とおくと、軸は\(\small x=a\)であることから、\(\small \color{red}{-2<a<2 \cdots ②} \)を満たす必要があることが分かる。
[3]境界での\(\small y\)座標
端点での\(\small y\)座標はいずれも正になるので
\begin{cases}
f(-2)=5a+6 \color{red}{>0}\\
\qquad \quad \Rightarrow \space \color{red}{a>-\dfrac{6}{5} \cdots③}\\
f(2)=-3a+6 \color{red}{>0}\\
\qquad \quad \Rightarrow \space \color{red}{a<2 \cdots④}\\
\end{cases}
③、④は両方とも同時に成り立つ必要があるので、共通範囲を考えることで、\(\small \color{red}{-\dfrac{6}{5}<a<2 \cdots ⑤}\)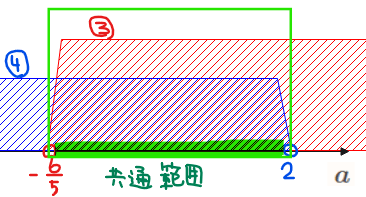
以上の[1]~[3]より、2つの実数解を持つ条件は①、②、⑤の共通範囲を考えることで\(\small \color{red}{-\dfrac{6}{5}<a≦1 \cdots ⑥}\).
■1つの実数解を持つ場合
これは、応用問題1の(1)の解答そのままなので、結果は \(\small \displaystyle \color{red}{a≦-\frac{6}{5}、2<a \cdots⑦}\)
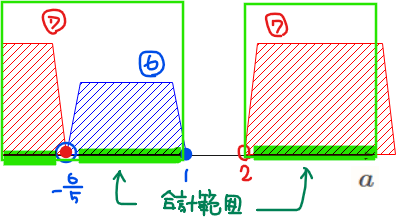
最後に⑥と⑦の合計範囲を考えることで答えになる(「2つの実数解を持つ場合」と「1つの実数解を持つ場合」のどちらかを満たせば少なくとも1つの実数解を持つといえるので合計範囲でOK)。
(解答)
\(\small \quad \displaystyle \color{red}{a≦1、2<a}\)
本記事のまとめ
今回は、解の配置問題について基本パターン3つの解き方と実際の問題を通して解き方の解説を行ってきました。ポイントをまとめると以下の通りです。
■2次方程式の解の配置問題の解き方
・STEP1:問題を満たす2次関数のグラフを図示
・STEP2:グラフをもとに3つの観点で条件を確認
- 判別式の条件
- 軸の範囲
- 境界での\(\small y\)座標
■解の配置問題の基本パターン
- パターン①:基準値以上/以下の実数解を持つ
- パターン②:ある区間内に実数解を持つ
- パターン③:基準値の左右に実数解を持つ
解の配置問題はいろいろな問題パターンがあるように感じますが、実はほとんどの問題が上記の3パターンに当てはまるようになっているので、問題集などで躓いたときはぜひ今回の内容を振り返って解き方を確認するようにしましょう。
では今回は以上です。お疲れさまでした!








コメント
■基準値以上の異なる2つの実数解を持つ場合
以下3つの条件の共通範囲を考えればOK。
・判別式:D>0
・軸の範囲:「軸」≧ 基準値
・境界でのy座標:「基準値でのy座標」≧0 ※基準値が境界になる
と記載されていますが、異なる2つの実数解で境界でのy軸≧0なので
軸の範囲は 軸>0 ではないのでしょうか?
どうぞ宜しくお願いします。
ご指摘ありがとうございますm(__)m
軸の範囲について改めて確認を行い一部誤りを修正しました。
(変更前)軸の範囲:「軸」≧ 基準値
(変更後)軸の範囲:「軸」> 基準値 ← 等号が不要
※「基準値以下の異なる2つの実数解を持つ場合」についても同様に修正
今回は『基準値以上』の異なる2つの実数解を持つ条件なので、軸は基準値より大きい範囲になる必要がありますね
(軸=基準値の場合は軸の左側の解が必ず基準値より小さくなってしまう…)。
今後も可能な限り正確な解説を心掛けてまいりますので、引き続きよろしくお願いします。
最後から二つ目と最後の問題でマイナスが何箇所か抜けています
当サイトをご覧いただきありがとうございます!
ご指摘の通り、符号のミスがありましたので、修正していますm(__)m
今後も可能な限り正確な解説を心掛けてまいりますので、引き続きよろしくお願いします。