【剰余の定理】すぐに使える裏ワザ紹介！基礎～難問までパターン別に解説（重解・虚数解ωの余りの計算）

今回は、剰余の定理について基本的な問題から応用問題までをパターン別に解説します。多くの人がつまずきやすい割り算の数式が重解や虚数解の場合といったパターンごとに解き方のコツや考え方の説明をしていきます。また、面倒な計算を省略できる裏技テクニックまで紹介しているので、ぜひ最後まで読んでみてください！

　本記事はこんな人におすすめ

剰余の定理を使った余りの計算についてパターンごとに解き方を知りたい！
重解や虚数解になる問題の解き方についてのわかりやすい解説がほしい！
数式に文字が含まれるような応用問題にもチャレンジしたい！
計算が大変なのでなるべく楽に解けるような裏技テクニックを教えてほしい！
剰余の定理と因数定理の違いが知りたい！

　本記事のレベル

重要度

低

1

2

3

4

5

高
難易度

易しい

1

2

3

4

5

難しい
暗記/理解

暗記重視

1

2

3

4

5

理解重視

【はじめに】剰余の定理とは
1. 剰余の定理とその意味
2. 剰余の定理と因数定理の違い
【パターン別】剰余の定理を使った問題
【まとめ】剰余の定理を使った問題の解き方

【はじめに】剰余の定理とは

剰余の定理とその意味

今回のテーマの「剰余の定理」の意味について簡単に振り返りをしておきましょう。

■剰余の定理
数式、$\small P(x)$を1次式$\small (x-a)$で割ったときの余りは$\small P(a)$.

理由は、商と余りの関係を数式化するとわかります。割り算には、「15÷7=2 余り1」のように

元の数：割り算される数
割る数：元の数を割り算する数
商：割り算の答え
余り：割り切れなかった端数

の4つの登場人物がいます。そしてこれらの数の間には「(元の数)=(割る数)×(商)+(余り)」という関係式が成り立ちます。実際に先程の例を見てみると、「15=7×2+1」が成り立ちますね。

この関係は数式の場合でも同じです。元の数式を$\small P(x)$、割る数式を$\small (x-a)$、商を$\small Q(x)$、余りを$\small R$とすると、

$$\color{red}{P(x)}=\color{blue}{(x-a)}Q(x)+\color{green}{R}$$

が成り立ちます。この式で、$\small x=a$を代入すると

$$
\begin{equation}
\begin{split}
\color{red}{P(a)}&=\color{blue}{(a-a)}Q(a)+\color{green}{R}\\
\color{red}{P(a)}&=\color{blue}{0}\cdot Q(a)+\color{green}{R}\\
\color{red}{P(a)}&=\color{green}{R}\\
\end{split}
\end{equation}
$$

つまり、もとの数式に$\small x=a$を代入した$\small P(a)$が余りになるというのが「剰余の定理」です。

剰余の定理と因数定理の違い

剰余の定理と似た定理に「因数定理」があります。因数定理とは、剰余の定理のうち、特に「余り=0」となる場合の定理です。

■因数定理
数式$\small P(x)$に対して、$\small P(a)=0$となるとき、数式$\small P(x)$は1次式$\small (x-a)$を因数に持つ。

剰余の定理の説明の時に出てきた

$$\color{red}{P(x)}=\color{blue}{(x-a)}Q(x)+\color{green}{R}$$

の数式の余り$\small \color{green}{R}=0$の場合なので、上記の関係式は

$$\color{red}{P(x)}=\color{blue}{(x-a)}Q(x)$$

になります。このように、$\small P(a)=0$の場合は、数式$\small P(x)$が$\small x-a$で因数分解できるというのが因数定理なので、一緒に覚えておきましょう。

【パターン別】剰余の定理を使った問題

ここからは、剰余の定理を使った問題を初級編、中級編、上級編に分けて解説していきます。

【初級編】剰余の定理を使った余りの求め方

基本問題

(1) 整式$\small P(x)$を$\small x-1$で割ると余りは5、$\small x-2$で割ると余りは7となる。このとき、$\small P(x)$を$\small x^2-3x+2$で割った余りを求めよ。
(2) $\small (x+1)^{12}$を$\small x^2-1$で割ったときの余りを求めよ。 (1)[近畿大],　(2)[日本歯大]

■剰余の定理を使った余りの求め方
①余りの次数を確認して文字でおき、②元の整式と余りの関係式を立ててから、③剰余の定理で文字を求めよ！

　①余りの次数は、割り算する数式の次数より低くなる。
　　例：1次式（$\small x-2$など）で割った余りは必ず定数。
　　　　2次式（$\small x^2+x-2$など）で割った余りは1次式以下。

　②元の式と余りの関係式は一般に
$$\color{red}{ \left[\mathbf{元の式}\space P(x) \right]}=\color{blue}{[\mathbf{割り算する式}]} \times [\mathbf{商}\space Q(x)]+\color{green}{[\mathbf{余りの式} \space R(x)]}$$
　③剰余の定理を使って連立方程式で解く

補足：2次式で割った余りが1次式以下になるのはなぜ？
理由をひとことでいうなら、「余りが2次式以上なら、まだ割ることで1次式以下にできるから」です。
余りというのは「もうそれ以上割れない端数」のことです。15÷7の余りが2なのは、2は7では割れないからです。もし、「15÷7=1 余り8」と答えたら…もちろん×ですよね。なぜなら、余りの8はまだ7で割ることができるからです。
これと同じで、ある数式を$\small x^2+1$で割った余りが$\small x^2+2x+2$だったとしましょう。するとこの余りはまだ$\small x^2+1$で割ることができて、計算すると$\small 2x+1$が余りになります。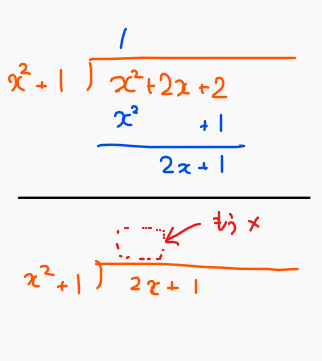

このように割り算を余りが2次式以上になっている場合は、割り算を繰り返すことで1次式以下にできます。
一般にはポイントの①に記載の通り、余りの次数は割り算する数式の次数より低くなります。

問題1：複数の条件から余りを求める問題

2つの関係式から余りを求める問題

整式$\small P(x)$を$\small x-1$で割ると余りは5、$\small x-2$で割ると余りは7となる。このとき、$\small P(x)$を$\small x^2-3x+2$で割った余りを求めよ。 [近畿大]

　解説

$\small P(x)$を2次式$\small x^2-3x+2$で割った余りは1次式以下になるので、$\small ax+b$とおける。整式$\small P(x)$と余りの関係式は

$$P(x)=(x^2-3x+2)Q(x)+\color{green}{ax+b}\quad \cdots(*)$$

剰余の定理から、$\small P(1)=5、P(2)=7$なので$\small (*)$にそれぞれ代入すると

$$P(1)=\color{green}{a+b}=5\quad \cdots①$$

$$P(2)=\color{green}{2a+b}=7\quad \cdots②$$

①、②を連立方程式として解くと、$\small a=2、b=3$。よって、余りは $\small 2x+3\cdots(答)$

　別解

■余りを求める裏技テクニック①
★で割った余りが●
→余りは「$\small a$★＋●」とおけ！

実は、余りを求める問題ではもう一つ別解があり、この方法を使うと連立方程式を解かなくて済むのでとても簡単に答えを求めることができます。

$\small x-1$で割った余りが5であることから、余りは$\small x-1$で割り切れる部分と端数の「5」の部分に分けることができるので

$$
\begin{equation}
\begin{split}
P(x)=(x-1)(x-2)Q(x)+\color{red}{a(x-1)+5}\quad \cdots(*)
\end{split}
\end{equation}
$$

とおくことができます。

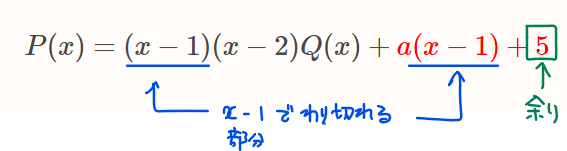
よって、$\small (*)$に$\small P(2)=7$を代入することで

$$
\begin{equation}
\begin{split}
P(\color{red}2)=&(\color{red}2-1)(\color{red}2-2)Q(\color{red}2)+a(\color{red}2-1)+5=7\\
&a+5=7\\
&a=2\\
\end{split}
\end{equation}
$$

ゆえに、余りは$\small a(x-1)+5=2(x-1)+5=\color{red}{2x+3}$.

（補足）
「$\small x-2$で割った余りが7」であることから、余りを$\small \color{red}{a(x-2)+7}$とおいても解けます。

問題2：$\small P(x)$と割り算する数式から余りを求める問題

$\small P(x)$と割り算する数式から余りを求める問題

$\small (x+1)^{12}$ を$\small x^2-1$ で割ったときの余りを求めよ。 [日本歯大]

　解説

$\small x^2-1$で割っていることから、余りは1次式以下。

$$
\begin{equation}
\begin{split}
(x+1)^{12}&=(x^2-1)Q(x)+R(x)\\
(x+1)^{12}&=(x+1)(x-1)Q(x)+R(x)\\
\end{split}
\end{equation}
$$

ここで、左辺は「$\small x+1$で割ると余りが0」であることから、裏技テクニック①より余りは$\small R(x)=a\color{red}{(x+1)}+\color{blue}0=a(x+1)\cdots①$とおける。

つまり

$$(x+1)^{12}=(x+1)(x-1)Q(x)+a(x+1)\quad\cdots(*)$$

上式の両辺に$\small x=1$を代入すると

$$
\begin{equation}
\begin{split}
2^{12}&=2\cdot 0\cdot Q(2)+2a\\
2a&=2^{12}\\
a&=2^{11}\\
a&=2048\\
\end{split}
\end{equation}
$$

よって、①に代入することで余りは $\small \color{red}{2048x+2048\cdots(答)}$.

（補足）
ここでは解説しませんが、余りを$\small ax+b$とおいて、$\small (*)$に$\small x=\pm 1$を代入して連立方程式で解く方法でも求めることができます。

類題

整式$\small P(x)$ を$\small x^2+1$ で割ると余りが1、$\small x+2$で割ると余りが11になるとき、$\small P(x)$を $\small (x^2+1)(x+2)$で割ったときの余りを求めよ。

　解説

3次式$\small (x^2+1)(x+2)$で割っているので、余りの次数は2次式以下です。そのため、「$\small x^2+1$ で割ると余りが1」であることから、余りは $\small a(x^2+1)+1\cdots①$ とおけます。

関係式

$$P(x)=(x^2+1)(x+2)Q(x)+a(x^2+1)+1$$

と剰余の定理、$\small \color{blue}{P(-2)=11}$より

$$
\begin{equation}
\begin{split}
\color{blue}{P(-2)}=&\color{red}{5\cdot 0\cdot }Q(\color{red}{-2})+\color{red}5a+1=\color{blue}{11}\\
&5a=10\\
&a=2\\
\end{split}
\end{equation}
$$

よって、余りは①に代入することで

$$
\begin{equation}
\begin{split}
2(x^2+1)+1= \color{red}{2x^2+3\space \cdots(答)}
\end{split}
\end{equation}
$$

（補足）
余りを$\small ax^2+bx+c$とおいて、剰余の定理で虚数の範囲まで考えることで
$$P(i)=1、P(-2)=11$$
が成り立つことを利用して連立方程式で解く方法もあります。ただ、この方法の場合、文字が3つの連立方程式を解く必要があり計算が大変なので、裏ワザの方法で解くのとかなり楽かなと思います。
ちなみに、虚数の範囲まで考える方法はこの後の問題で詳しく解説します。

【中級編】重解の割り算がでてくる問題

標準問題

(1) 整式 $\small x^4+ax^3+ax^2+bx-6$が整式 $\small x^2-2x+1$で割り切れるとき $\small a,b$の値を求めよ。
(2) $\small x^5+2x^2+1$ を$\small (x+1)^2$ で割ったときの余りを求めよ。 (1) [千葉大]

問題1：重解で割り切れる問題

重解で割り切れる問題

整式 $\small x^4+ax^3+ax^2+bx-6$が整式 $\small x^2-2x+1$で割り切れるとき $\small a,b$の値を求めよ。 [千葉大]

■重解で割り切れる問題の解き方のコツ
①2乗で割り切れる = 1乗でも割り切れる！
　→「1次式の余り=0」で因数定理を利用する

②勇気を出して割り算しよう！
　→1回割り算したあとに、商$\small Q(x)$に対して因数定理を利用

①について、(1)の問題であれば、$\small (x-1)^2$で割り切れるということは、$\small x-1$でも割り切れるということ。数式だとわかりにくいですが、数字に置き換えて考えるなら、要は25($\small =5^2$)で割り切れるなら5でも割り切れるということです。この特徴を使うことで解くことができます。

②については、「実際に割り算すれば計算できるけど面倒だしほかにもっといい方法があるはず…」と思い込んでしまい、手が止まってしまう人は多いですが、意外と解答はまじめに割り算していることもあるので、重解の問題では割り算を覚悟するくらいの気持ちで構えておくのがいいと思います。

ただし、別解で紹介する裏技テクニック②を使うことで割り算しなくても簡単に解くことができます。数Ⅲの学習範囲を含むので、既に学んでいる人はこのテクニックを使うのがよいでしょう。

　解説

$\small P(x)=x^4+ax^3+ax^2+bx-6$とおくと、$\small P(x)$ は$\small x-1$ で割り切れるため、剰余の定理(因数定理)から$\small P(1)=0$ が成り立ちます。

$$
\begin{equation}
\begin{split}
P(1)=&1+a+a+b-6=0\\
&\color{red}{2a+b=5 \quad \cdots①}\\
\end{split}
\end{equation}
$$

ここで、$\small P(x)$が$\small (x-1)^2$で割り切れるということは、$\small x-1$で2回割り算できるということなので、まず1回割り算してみると、その商$\small Q(x)$は

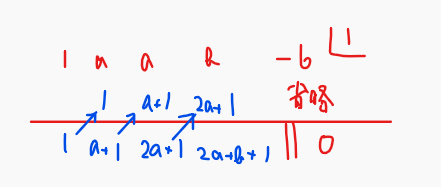
$$Q(x)=x^3+(a+1)x^2+(2a+1)x+2a+b+1$$

この$\small Q(x)$がさらに$\small x-1$で割り切れるということなので、因数定理から、$\small Q(1)=0$なので、

$$
\begin{equation}
\begin{split}
Q(1)=&1^3+(a+1)+(2a+1)+2a+b+1=0\\
&\color{red}{5a+b=-4\quad \cdots②}\
\end{split}
\end{equation}
$$

①、②の連立方程式を解くことで、$\small \color{red}{a=-3, b=11\quad \cdots(答)}$

　別解

■重解の割り算で使える裏技テクニック②
重解の割り算問題は微分で解ける！

数Ⅱを勉強中の人は、上記の解法が一般的な解き方ですが、数Ⅲの微分法を勉強した人であれば微分を使うことで、割り算せずに答えを求めることができます。「まだ勉強してない！」という人はひとまず飛ばしてokです。

①の関係式を出すところまでは同様です。$\small P(x)$が$\small (x-1)^2$で割り切れるので、商を$\small Q(x)$とおくと

$$x^4+ax^3+ax^2+bx-6=(x-1)^2Q(x)$$

が成り立ちます。この両辺を$\small x$で微分します。右辺の微分は関数$\small (x-1)^2$と$\small Q(x)$の積の微分になっているので、数Ⅲで学習する積の微分法を使うことで計算することができます。

■積の微分法
$$\{f(x)\cdot g(x)\}’=f'(x)g(x)+f(x)g'(x)$$

微分した式は

$$
\begin{equation}
\begin{split}
4x^3+3ax^2+2ax+b=2(x-1)Q(x)+(x-1)^2Q'(x)\\
\end{split}
\end{equation}
$$

となるので、両辺に$\small x=1$を代入してあげると

$$
\begin{equation}
\begin{split}
4+3a+2a+b&=0\\
\color{red}{5a+b} &\color{red}{=-4}\\
\end{split}
\end{equation}
$$

すると、本編の解説の式②の形になりました。あとは、本編の解説と同様になります。このように微分を使うことで割り算をせずに計算できるので時短で計算ミスも防げる点でおすすめです。ぜひ微分で解いてみてください！

問題2：重解で割った余りを求める問題

この問題は数Ⅲで学習する微分法を使います。未学習の人は飛ばしてください！

重解で割った余りを求める問題

(2) $\small x^5+2x^2+1$ を$\small (x+1)^2$ で割ったときの余りを求めよ。

　解説

2次式 $\small (x+1)^2$で割っているので、余りは1次式になります。ここで$\small x^5+2x^2+1$ を$\small x+1$ で割り算したときの余りは剰余の定理から

$$P(-1)=(-1)^5+2(-1)^2+1=2$$

なので、裏技テクニック①より求める余りは$\small a(x+1)+2\cdots①$とおけます。

よって、

$$x^5+2x^2+1=(x+1)^2Q(x)+a(x+1)+2 \quad \cdots②$$

あとは定数$\small a$を求めるのみですが、問題文の情報だけでは条件式が足りません。そこで、裏技テクニック②の通り微分を使います。

②の両辺を$\small x$で微分すると

$$5x^4+4x=2(x+1)Q(x)+(x+1)^2Q'(x)+a$$

両辺に$\small x=-1$を代入することで、

$$
\begin{equation}
\begin{split}
5\cdot \color{red}{(-1)^4}+4\cdot \color{red}{(-1)}&=2\cdot \color{red}0\cdot Q(0)+\color{red}0\cdot Q'(0)+a\\
5-4&=0+a\\
a&=1\\
\end{split}
\end{equation}
$$

あとは、①に代入することで、$\small a\cdot (x+1)+2=\color{red}{x+3\cdots(答)}$

【上級編】虚数解、文字を含む数式の割り算

応用問題

(1) 整式 $\small x^{2023}$を $\small x^2+1$で割った余りを求めよ。
(2) 整式 $\small x^{97}+3$を整式 $\small x^2+x+1$で割ったときの余りを求めよ。
(3) $\small n≧2$の自然数とする。整式$\small (x+1)^n$を$\small (x-1)^2$で割ったときの余り求めよ。

問題1：$\small x^2+1$で割り算した余りを求める問題

虚数を利用した余りの計算

整式 $\small x^{2023}$を $\small x^2+1$で割った余りを求めよ。

　解説

余りが1次式以下であることから、$\small ax+b$とおく。

$$x^{2023}=(x^2+1)Q(x)+ax+b\quad\cdots(*)$$

が成り立つ。$\small Q(x)$の項を消すために$\small (*)$に$\small x=i$を代入すると

$$i^{2023}=0+a i+b.$$

$\small i^2=-1、i^4=1$より、

$$
\begin{equation}
\begin{split}
i^{2023}&=0+a i+b\\
(i^4)^{505}\cdot i^2\cdot i&=b+ai\\
-i&=b+ai\\
\end{split}
\end{equation}
$$

恒等式なので、両辺の実部同士と虚部同士は一致することから、$\small a=-1、b=0$。

よって、余りは $\small \color{red}{-x\cdots(答)}$

問題2：虚数解ωを利用した余りの計算

応用問題

整式 $\small x^{97}+3$を整式 $\small x^2+x+1$で割ったときの余りを求めよ。

　解説

$$x^{97}+3=(x^2+x+1)Q(x)+ax+b \quad \cdots(*)$$

ここで通常は商$\small Q(x)$が邪魔なので係数である$\small x^2+x+1=0$となるような$\small x$を両辺に代入して定数$\small a、b$を求めるのですが、今回は$\small x^2+x+1=0$が明らかに虚数解なのでこのままだと少々面倒です。

そこで、一旦方程式$\small x^2+x+1=0$の解を$\small \omega$とおいておくと、実は$\small \omega$は$\small \omega^3=1$を満たします。なぜならば、

\begin{equation}
\begin{split}
\omega^3=&1\\
\omega^3-1=&0\\
(\omega-1)\color{red}{(\omega^2+\omega+1)}=&0\\
\end{split}
\end{equation}

ここで、$\small \omega = 1$は$\small x^2+x+1=0$の解ではないので、赤色部分の式が0になる、すなわち$\small x^2+x+1=0$の解になっていることが分かります。

これは、所見だと気が付くのが厳しいので、覚えちゃいましょう…。

なので、$\small (*)$の式で、両辺に$\small x=\omega$を代入すると

\begin{equation}
\begin{split}
\color{red}{\omega^{97}}+3&=\color{blue}{(\omega^2+\omega+1)}Q(\omega)+a\omega+b\\
\color{red}{(\omega^3)^{32}\cdot\omega}+3&=\color{blue}0\cdot Q(\omega)+a\omega+b\\
\color{red}{(1)^{32}\cdot\omega}+3&=a\omega+b\\
\omega+3&=a\omega+b\\
(a-1)\omega&=3-b\\
\end{split}
\end{equation}

途中赤字の式変形は$\small \omega^3=1$であることを使って計算が楽になるように式変形しています。また、青字の式変形は$\small \omega^2+\omega+1=0$を使っています。

この式は、$\small \omega $が虚数解であることに注意すると、一般的に左辺は虚数、一方で右辺は実数となっており矛盾してしまいます。虚数≠実数ですからね…。ということは、この式が成り立つためには左辺の$\small (a-1)\omega=0$(実数)でないといけないので、$\small \omega \neq 0$であることから、$\small a=1$。右辺も0でないとイコールにならないので、$\small b=3$。よって、余りは $\small x+3\cdots(答)$となります。

　別解

■$\small \color{red}{x^{n-1}+x^{n-2}+\cdots+x+1}$で割られる問題の裏技テクニック③
　$\small x^n \equiv 1 \pmod {x^{n-1}+x^{n-2}+\cdots+x+1}$から元の整式を復元せよ！

　■合同式
　$\small a$と$\small b$を$\small m$で割った余りが等しいとき
　$$\color{red}{ a \equiv b \pmod m}$$

　合同式(mod)を使うことで計算量が激減します。

$\small x^{97}+3$の余りを考えるのは次数が大きすぎて大変ですが、合同式を使ってもっと次数の低い式に置き換えて考えることができます。

$\small x^3-1$を$\small x^2+x+1$で割った余りが0（＝割り切れる）なので

\begin{equation}
\begin{split}
x^{3}-1 &\equiv 0 \pmod {x^2+x+1}\\
x^{3} &\equiv 1 \pmod {x^2+x+1}\\
\color{red}{(}x^{3} \color{red}{)^{32}} &\equiv 1^{\color{red}{32}} \pmod {x^2+x+1}\\
x^{96} &\equiv 1 \pmod {x^2+x+1}\\
x^{96}\cdot \color{red}x &\equiv 1\cdot \color{red}x \pmod {x^2+x+1}\\
x^{97} \color{red}{+3} &\equiv x \color{red}{+3} \pmod {x^2+x+1}\\
\end{split}
\end{equation}

よって、余りは$\small \color{red}{x+3}$と求まります。

合同式はあまりだけに注目する考え方なので、余りを$\small ax+b$とおいたり、実数と虚数の等式を解いたりしなくてもよいので、かなり計算量を減らすことができます。

問題3：2項定理を利用した余りの計算

2項定理を利用した余りの計算

$\small n≧2$の自然数とする。整式$\small (x+1)^n$を$\small (x-1)^2$で割ったときの余り求めよ。

■$\small (a+b)^n$の割り算の余り
　2項定理を利用して残る項を抽出せよ！
　→2項定理を使うことで実際に割り算しなくても余りの項を特定できる。

　　例：$\small (x+1)^4$を$\small x^2$で割った余りであれば、
　　　　次数が$\small x^2$以上の項は割り切れるので余りとして残るのは
$$(x+1)^4=x^4+4x^3+6x^2+\color{red}{4x+1}$$
　　次数が1次以下の項、すなわち$\small 4x+1$と求めることができます。

　解説

余りは1次式以下なので、$\small ax+b$とおいておきます。

整式$\small (x+1)^n$を$\small (x-1)^2$で割った商を$\small Q(x)$とすると

$$(x+1)^n=(x-1)^2Q(x)+ax+b.$$

数Ⅲ学習者であれば、重解の割り算なので裏技テクニック②の方針で上式の両辺を微分してあげれば答えを求めることができますが、今回は微分を使わない前提で解いていきます（微分の解き方は別解として載せておきます）。

左辺が$\small (a+b)^n$の形になっているので2項定理を使うことを考えます。

■2項定理
$$(a+b)^n={}_n C_{0}a^n+{}_n C_{1}a^{n-1}b+\cdots+{}_n C_{n-1}ab^{n-1}+{}_n C_{n}b^n$$

ここで、$\small (a+b)^n$を$\small b$で割ったときの余りを考えると

$$(a+b)^n={}_n C_{0}a^n+{}_n C_{1}a^{n-1}\color{red}b+\cdots+{}_n C_{n-1}a\color{red}{b^{n-1}}+{}_n C_{n}\color{red}{b^n}$$

の式からわかるように第2項目以降は$\small b$が1つ以上あるので、$\small b$で割り切れます。そのため、余りになるのは$\small b$が1つもない$\small {}_n C_{0}a^n=a^n$になります。

同様に考えると、$\small (a+b)^n$を$\small b^2$で割ったときの余りは

$$\color{red}{{}_n C_{0}a^n+{}_n C_{1}a^{n-1}b=a^n+na^{n-1}b\quad \cdots①}$$

($\small b$が0個、1個しかない項が残る)になります。

2項定理のこの性質を使って問題の余りを考えていきましょう。2項定理の形に寄せるために$\small x-1=b$とおきます。すると$\small x=b+1$なので

$$(\color{red}x+1)^n=(\color{red}{(b+1)}+1)^n=(2+b)^n$$

よって、今考えている問題は$\small (2+b)^n$を$\small b^2$で割ったときの余りなので、これは式①で$\small a=2$の場合に相当します。よって、余りは$\small 2^n+n\cdot2^{n-1}b$となり、$\small x-1=b$で、$\small x$の式に戻してあげると

$$
\begin{equation}
\begin{split}
&2^n+n\cdot2^{n-1}(x-1)\\
=&\color{blue}{2^n}+n\cdot2^{n-1}x-n\cdot2^{n-1}\\
=&n\cdot2^{n-1}x-n\cdot2^{n-1}+\color{blue}{2\cdot2^{n-1}}\\
=&\color{red}{n\cdot2^{n-1}x-(n-2)\cdot2^{n-1}\quad\cdots(答)}\\
\end{split}
\end{equation}
$$

　別解

微分を使えば機械的に余りを求めることができます。

$$(x+1)^n=(x-1)^2Q(x)+ax+b\quad \cdots(*)$$

上式の両辺に$\small x=1$を代入して

$$2^n=a+b\quad \cdots②$$

$\small (*)$の両辺を$\small x$で微分すると

$$n(x+1)^{n-1}=2(x-1)Q(x)+(x-1)^2Q'(x)+a$$

両辺に$\small x=1$を代入して

$$n\cdot 2^{n-1}=a\quad \cdots ③$$

②に③を代入することで

$$
\begin{equation}
\begin{split}
&2^n=n\cdot2^{n-1}+b\\
&b=(2-n)2^{n-1}\quad\cdots④\\
\end{split}
\end{equation}
$$

よって、③、④より、余りは $\small \color{red}{n\cdot 2^{n-1}x+(2-n)2^{n-1}\cdots(答)}$ .

類題

整式 $\small x^{2023}-1$を整式 $\small x^4+x^3+x^2+x+1$で割ったときの余りを求めよ。 [京都大]

　解説

裏技テクニック③より、整式$\small x^4+x^3+x^2+x+1$で割り算していることから、$\small x^5 \equiv 1 \pmod{x^4+x^3+x^2+x+1}$で考えます。

2023は5で割ると404余り3なので、

\begin{equation}
\begin{split}
x^5 &\equiv 1 \pmod{x^4+x^3+x^2+x+1}\\
\color{red}{(}x^5\color{red}{)^{404}} &\equiv 1^{\color{red}{404}} \pmod{x^4+x^3+x^2+x+1}\\
x^{2020} &\equiv 1 \pmod{x^4+x^3+x^2+x+1}\\
x^{2020} \color{red}{\cdot x^3}&\equiv 1 \color{red}{\cdot x^3} \pmod{x^4+x^3+x^2+x+1}\\
x^{2023} \color{red}{-1}&\equiv x^3\color{red}{-1} \pmod{x^4+x^3+x^2+x+1}\\
\end{split}
\end{equation}

よって、余りは $\small \color{red}{x^3-1\cdots(答)}$になります。

【まとめ】剰余の定理を使った問題の解き方

今回は、剰余の定理を使った問題について解説しました。

整式の余りを求める問題は基本的は以下の方針で解くことができることを説明しました。

■剰余の定理を使った余りの求め方
①余りの次数を確認して文字でおき、②元の整式と余りの関係式を立ててから、③剰余の定理で文字を求めよ！

　①余りの次数は、割り算する数式の次数より低くなる。

　②元の式と余りの関係式は一般に
$$\color{red}{ \left[\mathbf{元の式}\space P(x) \right]}=\color{blue}{[\mathbf{割り算する式}]} \times [\mathbf{商}\space Q(x)]+\color{green}{[\mathbf{余りの式} \space R(x)]}$$
　③剰余の定理を使って連立方程式で解く

その他によくある問題パターンの解き方のコツについても解説しました。