三角比の基本公式の効率な覚え方（180°±θ、90°±θなど全パターンを解説）

本記事では、三角関数のかかわる公式の攻略法を解説します。物量が多いため、何回かに分けて解説してこうと思います。

三角関数の分野は、公式の種類が多いうえに、それぞれの公式に$\small \sin\theta、\cos\theta、\tan\theta$の3種類があるので単純に覚える量も3倍になります。

今回はこの難関分野を、公式を極力覚えずに攻略するための必勝法を完全解説していきたいと思います。

はじめに
★本記事で扱う公式
★公式の解説
1. 覚えるべきポイント
まとめ

はじめに

この記事では、数学で挫折してしまう人の多くが悩みとして抱えている「公式が多すぎて覚えられない…」という悩みに対して、公式を極力覚えなくてもよい方法を伝授します。結論、覚える量を減らすために重要なことは以下3つです。

公式を丸暗記しない
公式を忘れたとしても導けるようにする
覚える部分と覚えない部分を見極める

多くの公式は覚えなくても、少し考えれば導けます。なので、公式を導くために必要な最低限の知識だけ覚えておけばOKです。これだけでも覚える量が減ってだいぶ楽になると思います。

また、公式の中には覚えなくてはいけない公式と覚えてはいけない公式の2種類があります。
覚えなくてはいけない公式とは、式を導くのに時間がかかるものや導く方法自体が難しいものです。そのような公式は逆に公式だけ覚えてしまった方が効率的です。
一方で覚えてはいけない公式とはその逆で、導くことが簡単で理解してしまえば当たり前すぎてあえて公式化する必要がないものです。簡単に導けるようなものは、結果ではなく根幹の知識だけ理解しておけばOKというわけです。

では、今回も覚える公式を減らしていきましょう！

★本記事で扱う公式

三角関数の諸公式

三角関数の諸公式Ⅰ

$$ \begin{equation} \begin{split} &\sin(\theta+2n\pi)=\sin\theta\\ &\cos(\theta+2n\pi)=\cos\theta\\ &\tan(\theta+2n\pi)=\tan\theta\\ \end{split} \end{equation} $$

三角関数の諸公式Ⅱ

$$ \begin{equation} \begin{split} &\sin(-\theta)=-\sin\theta\\ &\cos(-\theta)=\cos\theta\\ &\tan(-\theta)=-\tan\theta\\ \end{split} \end{equation} $$

三角関数の諸公式Ⅲ

$$ \begin{equation} \begin{split} &\sin(\pi\pm\theta)=\mp\sin\theta\\ &\cos(\pi\pm\theta)=-\cos\theta\\ &\tan(\pi\pm\theta)=\pm\tan\theta\\ \end{split} \end{equation} $$

三角関数の諸公式Ⅳ

$$ \begin{equation} \begin{split} &\sin\left( \frac{\pi}{2}\pm\theta \right)=\cos\theta\\ &\cos\left(\frac{\pi}{2}\pm\theta\right)=\mp\sin\theta\\ &\tan\left(\frac{\pi}{2}\pm\theta\right)=\mp\frac{1}{\tan\theta}\\ \end{split} \end{equation} $$

三角関数の諸公式のスペック

使用頻度

低

1

2

3

高
導出難易度

易しい

1

2

3

難しい
暗記/理解

暗記重視

1

2

3

理解重視

加法定理

加法定理

$$ \begin{equation} \begin{split} &\sin(\alpha\pm\beta)=\sin\alpha\cos\beta\pm\cos\alpha\sin\beta\\ &\cos(\alpha\pm\beta)=\cos\alpha\cos\beta\mp\sin\alpha\sin\beta\\ &\tan(\alpha\pm\beta)=\frac{\tan\alpha\pm\tan\beta}{1\mp\tan\alpha\tan\beta}\\ \end{split} \end{equation} $$

加法定理のスペック

使用頻度

低

1

2

3

高
導出難易度

易しい

1

2

3

難しい
暗記/理解

暗記重視

1

2

3

理解重視

★公式の解説

覚えるべきポイント

今回解説する公式だけでもかなりの数があって、「既におなかいっぱい…」という人も多いと思いますが、安心してください、実は、覚えるべきことは2つしかありません。

■これだけ覚えろ
　加法定理のこれだけ覚えろ。
　・$\small \sin(\alpha+\beta)=\sin\alpha\cos\beta+\cos\alpha\sin\beta$
　・$\small \cos(\alpha+\beta)=\cos\alpha\cos\beta-\sin\alpha\sin\beta$

どうでしょう？「2つも覚えるのかよ…」と感じた人もいると思いますが、冒頭に紹介したあれだけたくさんあった公式をこの2つの公式だけ覚えればイケると考えると、かなりコスパはいいんじゃないかなと思います。

一方で、公式2つとは言ったものの結構長くて複雑なので、個人的なこの2つの公式の覚え方も併せて伝授しちゃいます。

■加法定理の覚え方
　・$\small \sin(\alpha+\beta)=\sin\alpha\cos\beta+\cos\alpha\sin\beta$
　　→サインコサイン+コサインサイン
　・$\small \cos(\alpha+\beta)=\cos\alpha\cos\beta-\sin\alpha\sin\beta$
　　→コスコス-サインサイン　※「コス」はコサインのこと

　★ポイント
　　・サインやコサインの後の角度は$\small \alpha$が最初、$\small \beta$が最後の順番なので覚えない。

かなり頭おかしめな覚え方ですが、口ずさんでいるうちに自然と覚えられるので、明日からはごはん前にこの公式を唱えてから食べるようにしましょう。

加法定理の攻略法

加法定理は、先程の覚えるべきポイントの公式を覚えれば、9割は完成です。
他の公式の導き方はそれぞれ下にまとめたので確認してみてください。

■加法定理の覚え方
　step1：$\small \sin(\alpha+\beta)$と$\small \cos(\alpha+\beta)$の公式を覚える。
　step2：$\small \sin(\alpha\color{red}-\beta)$と$\small \cos(\alpha\color{red}-\beta)$は、足し算と引き算を変えるだけ。
　step3：$\small \tan(\alpha\pm\beta)=\frac{\sin(\alpha\pm\beta)}{\cos(\alpha\pm\beta)}$で導出可能。

■$\small \tan(\alpha+\beta)$公式の導出方法
$$
\begin{equation}
\begin{split}
\tan(\alpha+\beta)&=\frac{\sin(\alpha+\beta)}{\cos(\alpha+\beta)}\\
&=\frac{\sin\alpha\cos\beta+\cos\alpha\sin\beta}{\cos\alpha\cos\beta-\sin\alpha\sin\beta}\\
&=\cfrac{\frac{\sin\alpha\cos\beta}{\cos\alpha\cos\beta}+\frac{\cos\alpha\sin\beta}{\cos\alpha\cos\beta}}{1-\frac{\sin\alpha\sin\beta}{\cos\alpha\cos\beta}}\quad \cdots(※)\\
&=\frac{\tan\alpha+\tan\beta}{1-\tan\alpha\tan\beta}\\
\end{split}
\end{equation}
$$
　　※2行目から3行目にかけた式は、分母分子を$\small \cos\alpha\cos\beta$で割り算してます。

$\small \tan(\alpha-\beta)$も同様に導出できるのでぜひ自身でやってみましょう。

三角関数の諸公式Ⅰの攻略法

三角関数の諸公式Ⅰ

$$ \begin{equation} \begin{split} &\sin(\theta+2n\pi)=\sin\theta\\ &\cos(\theta+2n\pi)=\cos\theta\\ &\tan(\theta+2n\pi)=\tan\theta\\ \end{split} \end{equation} $$

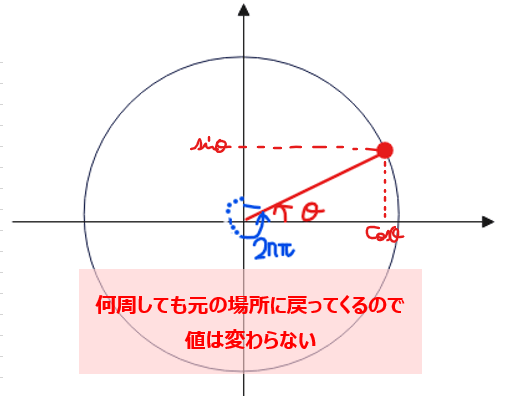
この公式は、単位円を思い浮かべれば意味的に理解できます。$\small 2n\pi$は360°(1周)×$\small n$=$\small n$周なので、つまり「円を$\small n$周回っても元の位置にもどる（$\small =$三角関数の値は変わらない）」ということを表した公式です。なので意味だけ理解できてれば覚えなくて大丈夫です。

三角関数の諸公式Ⅱの攻略法

三角関数の諸公式Ⅱ

$$ \begin{equation} \begin{split} &\sin(-\theta)=-\sin\theta\\ &\cos(-\theta)=\cos\theta\\ &\tan(-\theta)=-\tan\theta\\ \end{split} \end{equation} $$

これも、単位円でイメージすればすぐに理解できるので暗記不要です。$\small \sin(\color{blue}{-\theta})$というのは、角度が$\small \color{blue}{-\theta}$ということで、単位円で描くならば下図の青色の角度のことです。

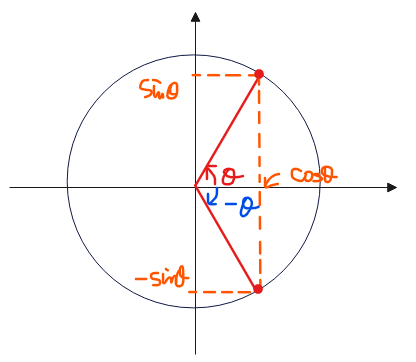
サインの値がいわゆる$\small “y”$座標、コサインの値がいわゆる$\small “x”$座標なので、$\small \sin(\color{blue}{-\theta})$の値は、$\small \sin\color{red}{\theta}$の値と比較すると、いわゆる$\small “y”$座標が反転しただけなので、サインの値も符号が入れ替わるだけということです。

一方で、$\small \cos(\color{blue}{-\theta})$は反転してもいわゆる$\small “x”$座標は変わらないので、$\small \cos\color{red}{\theta}$と値は変わらないということです。

$\small \tan{(-\theta)}$については、いつも通り、$\small \frac{\sin(-\theta)}{\cos(-\theta)}=\frac{-\sin\theta}{\cos\theta}=-\tan\theta$で求められるので、覚えずに導き出せばokです。

三角関数の諸公式Ⅲ、Ⅳの攻略法

三角関数の諸公式Ⅲ

$$ \begin{equation} \begin{split} &\sin(\pi\pm\theta)=\mp\sin\theta\\ &\cos(\pi\pm\theta)=-\cos\theta\\ &\tan(\pi\pm\theta)=\pm\tan\theta\\ \end{split} \end{equation} $$

三角関数の諸公式Ⅳ

諸公式Ⅲ、Ⅳについては、一気にまとめて解説します。
結論、加法定理を使えば導き出せるので、暗記不要です。

具体的に2つほど実際に導出してみます。

■諸公式Ⅲ：$\small \sin(\pi＋\theta)=-\sin\theta$の導出
サインの角度が足し算になっているので、加法定理の「サインコサイン+コサインサイン」、つまり$\small \sin(\alpha+\beta)=\sin\alpha\cos\beta+\cos\alpha\sin\beta$で$\small \alpha=\pi,\beta=\theta$をあてはめると
$$
\begin{equation}
\begin{split}
\sin(\pi+\theta)&=\color{red}{\sin\pi}\cos\theta+\color{blue}{\cos\pi}\sin\theta\\
&=\color{red}0 \cdot \cos\theta+\color{blue}{(-1)} \cdot \sin\theta\\
&=-\sin\theta \cdots \text{導出完了}
\end{split}
\end{equation}
$$

■諸公式Ⅳ：$\small \cos\left(\frac{\pi}{2}-\theta\right)=\sin\theta$の導出
今回は加法定理の「コスコス＋サインサイン（※角度が引き算なので足し算引き算が逆になる）」、すなわち$\small \cos(\alpha-\beta)=\cos\alpha\cos\beta+\sin\alpha\sin\beta$で$\small \alpha=\frac{\pi}{2},\beta=\theta$をあてはめると
$$
\begin{equation}
\begin{split}
\cos\left(\frac{\pi}{2}-\theta\right)&=\color{red}{\cos\frac{\pi}{2}}\cos\theta+\color{blue}{\sin\frac{\pi}{2}}\sin\theta\\
&=\color{red}0 \cdot \cos\theta+\color{blue}{1} \cdot \sin\theta\\
&=\sin\theta \cdots \text{導出完了}
\end{split}
\end{equation}
$$

このように、加法定理を覚えていれば、これらの公式は暗記不要なので、覚える量をだいぶ減らすことができます。