今回は、三角関数の諸公式の一つ、積和、和積の公式について攻略法を解説していきます。
はじめに
三角関数は数学分野の中でも出てくる公式が桁違いに多い分野なので、公式暗記に苦戦している人も多いと思います。この記事では、そんな人に向けて、公式を覚えるために抑えるべきポイントや、そもそも公式を暗記した方が良いのかなどについて解説しています。
この記事を通して、少しでも公式暗記で困る人が少なくなればと思っているので、ぜひ最後まで読んで、公式攻略を目指していきましょう!
★本記事で扱う公式
積和(和積)の公式
公式のスペック
★公式の攻略法
積和・和積の公式は暗記不要
はじめに、積和・和積の公式の攻略法について結論をお伝えすると、「暗記不要」でいいと思います。
理由としては、
- 使用頻度が低いため暗記してもすぐ忘れる可能性が高い
- 加法定理から導出可能であり、導出方法も簡単
という点が挙げられます。
ちなみに、通常の参考書では和積の公式も積和の公式も4つずつの計8つが載っていると思いますが、本質的には冒頭に記載した3つずつの計6つ公式を抑えていれば問題ないので、ここではこの6つのみ記載しています。どういう意味かは後ほど説明するので、今は6つの公式だけ抑えればいいんだな程度で思ってもらえれば大丈夫です。
では、ここからは具体的な導出方法について解説していきます。
【解説の前に…】積和・和積の公式は本当は6つだけ!?
公式の導出方法を解説する前に、まずは先程お伝えした「6つの公式だけ抑えておけばok」の意味について触れておきます。
多くの教科書や参考書では8つの公式が載っており、冒頭の公式以外に以下の公式も載っていると思います。
結論、これらの公式は以下の公式と同じことを言っているので、本質的には同じ公式です。
1つ目の積和の公式は、\(\small \sin\alpha\cos\beta\)と\(\small \sin\beta\cos\alpha\)で角度部分の\(\small \alpha\)と\(\small \beta\)が入れ替わっただけで、サインとコサインの積をサインとコサインの和で表すことができるという公式の意味自体は同じです。
「公式の意味自体は同じ」というのがどういうことかというと、例えば、
$$\cos\frac{\pi}{8}\sin\frac{\pi}{5}\text{をサインとコサインの和で表せ。}$$
という問題があったとしましょう。このとき
■解法①
$$\cos\alpha\sin\beta = \frac{1}{2}(\sin(\alpha+\beta)-\sin(\alpha-\beta))$$
の公式で、\(\small \alpha=\frac{\pi}{8},\beta=\frac{\pi}{5}\)として計算する。
という解法で解いてもよいですし、\(\small \cos\frac{\pi}{8}\sin\frac{\pi}{5}=\sin\frac{\pi}{5}\cos\frac{\pi}{8}\)(掛け算は順番を入れ替えてもok)と捉えて、
■解法②
$$\sin\alpha\cos\beta = \frac{1}{2}(\sin(\alpha+\beta)+\sin(\alpha-\beta))$$
の公式で、\(\small \alpha=\frac{\pi}{5},\beta=\frac{\pi}{8}\)として計算する。
という解法で解いても、結果は同じになります。
実際に、\(\small \sin\alpha\cos\beta\)の公式で\(\small \alpha\)と\(\small \beta\)を入れ替えると、
$$
\begin{equation}
\begin{split}
&\sin\color{darkorange}\alpha\cos\color{green}\beta = \frac{1}{2}(\sin(\color{darkorange}\alpha+\color{green}\beta)+\sin(\color{darkorange}\alpha-\color{green}\beta))\\
&\color{blue}{\qquad \text{↓ }\quad \alpha\text{と}\beta\text{を入れ替えると…}}\\
&\sin\color{green}\beta\cos\color{darkorange}\alpha = \frac{1}{2}(\sin(\color{green}\beta+\color{darkorange}\alpha)+\sin(\color{green}\beta-\color{darkorange}\alpha))\\
&\qquad \qquad \space \space =\frac{1}{2}\left(\sin(\alpha+\beta)+\sin \{\color{red}{-(\alpha-\beta)}\}\right)\\
&\qquad \qquad \space \space =\frac{1}{2}\left(\sin(\alpha+\beta)\color{red}-\sin(\color{red}{\alpha-\beta})\right)\\
\end{split}
\end{equation}
$$
(最後の赤字部分は、三角関数の基本公式\(\small \sin(-\theta)=-\sin\theta\)を利用)。こんな感じで、導くことができちゃいます。
つまり、これらの公式はどちらも本質的には同じなので1つだけ覚えておけばよいわけです。
和積の公式も同じように\(\small \sin(-\theta)=-\sin\theta\)を使うと
$$
\begin{equation}
\begin{split}
\sin A-\sin B&=\sin A+\sin(-B)\\
\end{split}
\end{equation}
$$
と捉えることができるので、サインの和積の公式
$$\sin A+\sin B=2\sin\frac{A+B}{2}\cos\frac{A-B}{2}$$
で\(\small B→-B\)と置き換えてあげれば導くことができます。
このことから、これら2つの公式はあえて覚える必要がないため、本質的には6つの公式を覚えることができれば和積・積和の公式をマスターしたことになるわけです。
積和の公式の導出方法
前置きが長くなりましたが、ここから本題の積和の公式を導出する方法を解説します。慣れれば頭の中でできるようになります。
導出のコツを一言でいうとこんな感じです。
■積和の公式導出のコツ
サインとコサインの積の組み合わせを見て、加法定理を足し引きせよ!
具体例で解説します。たとえば、
$$\sin\alpha\cos\beta = \frac{1}{2}(\sin(\alpha+\beta)+\sin(\alpha-\beta))$$
を導きたいとしましょう。
導出には、おなじみの加法定理を使います。加法定理を思い浮かべたときに、今回左辺にある\(\small \sin\alpha\cos\beta\)のようなサインとコサインの積が出てくる公式を探します。すると、サインの加法定理が思い浮かぶと思います。
$$
\begin{equation}
\begin{split}
&\sin(\alpha+\beta)=\sin\alpha\cos\beta+\cos\alpha\sin\beta\cdots①\\
&\sin(\alpha-\beta)=\sin\alpha\cos\beta-\cos\alpha\sin\beta\cdots②\\
\end{split}
\end{equation}
$$
この式を並べてみてみると、①+②をすると第2項目が打ち消し合って、ちょうど求めたい\(\small \sin\alpha\cos\beta\)が残ります。
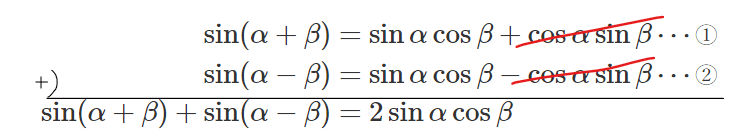
最後に両辺を2で割ってあげれば積和の公式になります。
$$\frac{1}{2}(\sin(\alpha+\beta)+\sin(\alpha-\beta))=\sin\alpha\cos\beta$$
他の公式も同じように導出できます。
和積の公式の導出方法
和積の公式もやっぱり加法定理から導出します。
■和積の公式導出のコツ
・サイン(またはコサイン)の和は加法定理のサイン(またはコサイン)の2公式で
\(\small \alpha+\beta=A,\alpha-\beta=B\)とおいて足し算せよ!
・サイン(またはコサイン)の差は加法定理のサイン(またはコサイン)の2公式で
\(\small \alpha+\beta=A,\alpha-\beta=B\)とおいて引き算せよ!
こちらも具体例で解説します。
たとえば、\(\small \cos A-\cos B\)を積の形で表したいときは、まずは加法定理のコサインの公式を書きます。
$$
\begin{equation}
\begin{split}
&\cos(\alpha+\beta)=\cos\alpha\cos\beta-\sin\alpha\sin\beta\cdots③\\
&\cos(\alpha-\beta)=\cos\alpha\cos\beta+\sin\alpha\sin\beta\cdots④\\
\end{split}
\end{equation}
$$
次に、\(\small \cos A-\cos B\)の形に寄せにいくために、\(\small \alpha+\beta=A,\alpha-\beta=B\)とおきます。この時、
$$
\begin{equation}
\left\{ \,
\begin{aligned}
\alpha+\beta=A\\
\alpha-\beta=B\\
\end{aligned}
\right.
\end{equation}
$$
の連立方程式を解くことで、\(\small \alpha=\frac{A+B}{2}\)、\(\small \beta=\frac{A-B}{2}\)となることに注意して、式③、④は
$$
\begin{equation}
\begin{split}
&\cos A=\cos\color{red}{\frac{A+B}{2}}\cos\color{red}{\frac{A-B}{2}}-\sin\color{red}{\frac{A+B}{2}}\sin\color{red}{\frac{A-B}{2}}\\
&\cos B=\cos\color{red}{\frac{A+B}{2}}\cos\color{red}{\frac{A-B}{2}}+\sin\color{red}{\frac{A+B}{2}}\sin\color{red}{\frac{A-B}{2}}\\
\end{split}
\end{equation}
$$
最後は、この式をもとに求めたい\(\small \cos A-\cos B\)を計算すればよいので
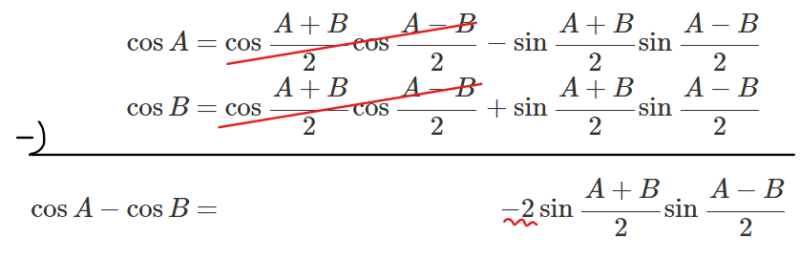
こんな感じで他の公式も求めることができます。
まとめ
今回は、積和・和積の公式の攻略法を解説しました。今回も加法定理をもとに公式を導出できることが分かりました。ささっと公式を導出できるようになるまで導出練習をして、暗記する公式を減らしていきましょう!
今回紹介した公式以外にも、様々な三角関数関連の諸公式の攻略法を解説しているので、この機会に是非、他の公式も合わせて攻略法をチェックしておきましょう!
- 三角比の基本公式の効率な覚え方(180°±θ、90°±θなど全パターンを解説)
- 2倍角、半角、3倍角の公式(sin、cos、tan)をまとめて覚える方法とは?
- 三角関数の合成公式の証明と使い方を分かりやすく解説
本日はここまでです。お疲れさまでした!




