今回は、余弦定理について解説していきます。平面図形の分野では非常によく使う定理なのでちょっとでも不安だなと感じた人はこの機会に復習しておきましょう!
はじめに
図形の分野で三角比を習った後に出てくるのが正弦定理と余弦定理です。この2公式は図形の分野では頻出の絶対に忘れてはいけない公式です。そんな2公式のうち、今回は余弦定理の攻略法について、公式の意味や覚え方を徹底解説していくので、ぜひ最後まで読んでみてください!
★本記事で扱う公式
余弦定理とは
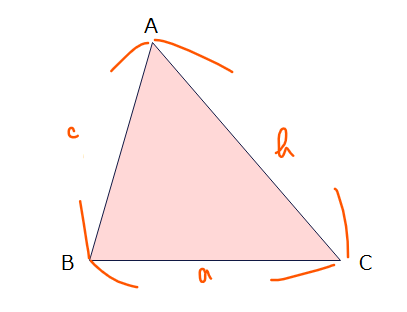
余弦定理のスペック
★余弦定理の攻略法
余弦定理は暗記がおすすめ
余弦定理の攻略法としては暗記するのがおすすめです。
そして本記事の結論となる「余弦定理の覚え方」をはじめにお伝えするとこんな感じです。
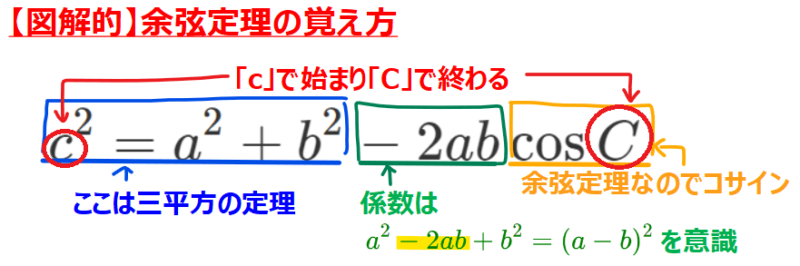
なんとなくわかる部分とよくわからない部分があると思いますが、大丈夫です。
この記事を最後まで読めば誰でも必ず理解できるようになるので、一つずつ理解していきましょう!
暗記したほうが良い理由
暗記をすすめる理由としては、
- 使用頻度が高く導出が面倒
- 「三平方の定理の一般形」と捉えることで暗記もしやすい
という点が挙げられます。
余弦定理の導出方法
余弦定理の導出方法を紹介します。公式自体は3つありますが、導出方法は全部同じなのでここでは1つだけ解説します。
■\(\small c^2=a^2+b^2-2ab\cos C\)の導出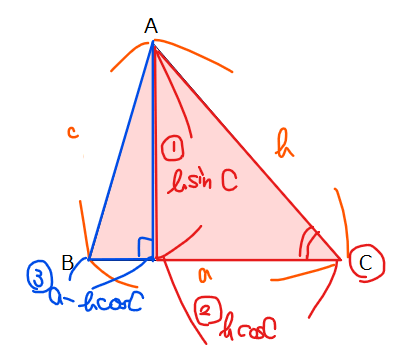
まずは上図のように、△ABCを右半分の直角三角形(赤色)と左半分の直角三角形(青色)に分けてみます。赤色の三角形について、縦辺と横辺はそれぞれ\(\small b\sin C\cdots①\)、\(\small b\cos C\cdots②\)(※よくわからない人はこちらへ)になります。
続いて青色の三角形を見ると縦辺はさっき求めた通り\(\small b\sin C\)、横辺はBC=\(\small a\)と②より、\(\small a-b\cos C\cdots③\)。
最後に青色の直角三角形において、三平方の定理から
$$
\begin{equation}
\begin{split}
&c^2=(b\sin C)^2+(a-b\cos C)^2\\
&c^2=\color{red}{b^2\sin^2 C}+a^2-2ab\cos C+\color{red}{b^2\cos^2 C}\\
&c^2=\color{red}{b^2\sin^2 C+b^2\cos^2 C}+a^2-2ab\cos C\\
&c^2=\color{red}{b^2(\sin^2 C+\cos^2 C)}+a^2-2ab\cos C\\
&c^2=\color{red}{b^2\cdot1}+a^2-2ab\cos C\\
&c^2=a^2+b^2-2ab\cos C\\
\end{split}
\end{equation}
$$
■補足説明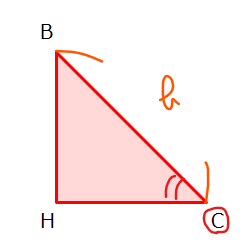
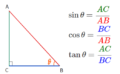
①と②の式がどこから出てきたかというと、サイン、コサインの定義から計算すると出てきます。
サインの定義より
$$
\begin{equation}
\begin{split}
&\sin C = \frac{\mathrm{BH}}{b}\\
&→\color{red}{\mathrm{BH} = b\sin C \quad \cdots \textrm{①の式}}\\
\end{split}
\end{equation}
$$
コサインの定義より、
$$
\begin{equation}
\begin{split}
&\cos C = \frac{\mathrm{CH}}{b}\\
&→\color{red}{\mathrm{CH} = b\cos C \quad \cdots \textrm{②の式}}\\
\end{split}
\end{equation}
$$
こんな感じで導出できますが、毎回導くには結構大変かなと思います。
「余弦定理」=「三平方の定理の一般形」と捉える
導出しないとなると公式を暗記する必要がありますが、そのまま丸暗記するのは大変ですし、すぐ忘れてしまいます。そこで、暗記する際には「すでに覚えているもの」と結びつけると覚えやすいと思います。
今回の余弦定理は、実は中学生で習う「三平方の定理」を一般化した定理と捉えると覚えやすいです。どういうことかというと、三平方の定理は「直角三角形」の場合しか使えない定理でした。一方で、余弦定理はどんな三角形でも使ことができる定理であり、どんな場面でも使える幅広さを持っています。
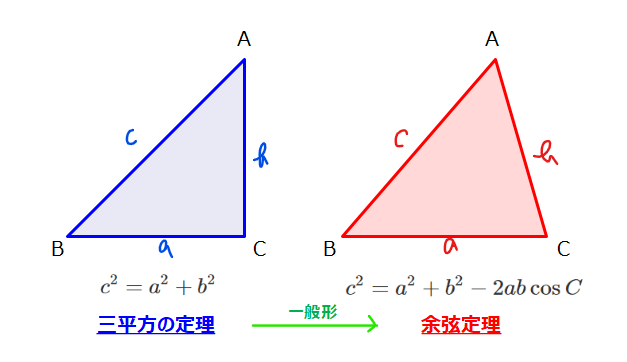
このように三平方の定理と余弦定理を並べてみてみると公式自体も結構似ていることが分かります。

余弦定理は三平方の定理に加えておまけの項がついているイメージです。
余弦定理=三平方の定理+おまけ項
余弦定理は、三平方の定理\(\small c^2=a^2+b^2\)におまけ項\(\small -2ab\cos C\)がついているイメージで覚えるのが良いと思います。
ここからは、「おまけ項」の意味についてもう少し深堀してみます。
【おまけ項の考察】符号について
まずは、おまけ項\(\small -2ab\cos C\)の符号についてです。三平方の定理が使える直角三角形を基準として考えると、以下のような鋭角三角形(赤色)は斜辺に相当する\(\small c\)が直角三角形(青色)の斜辺よりも必ず短くなります。
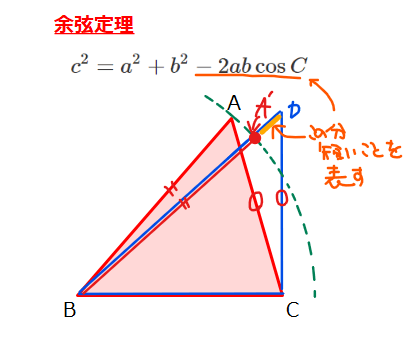
直角三角形(青色)を考えて斜辺DBとABの長さを比較すると、
AB=A’Bとなり、求める辺ABの長さ(余弦定理)はA’D分だけ
斜辺DBの長さ(三平の定理)より短くなる。
逆に、鈍角三角形であれば、角Cを鈍角とした場合三平方の定理で求める斜辺\(\small c\)よりも長くなりますが、角C=鈍角(\(\small 90° < C < 180°\))では、\(\small \cos C<0\)なので余弦定理のおまけ項全体では、\(\small -2ab\cos C>0\)となり、直角三角形の斜辺よりも長くなることを表しているといえます。
このように、おまけ項は三平方の定理の斜辺の長さを基準に長さを調整する項だということが分かります。
【おまけ項の考察】長さ調節の具体例
次におまけ項の具体例について説明します。先程、おまけ項は長さを調節する項といいましたが、どういうことか分かりやすく具体例で説明しましょう。
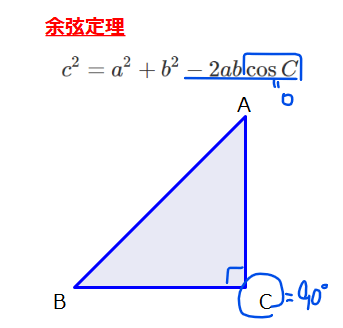
\(\small \angle C=90°\)は上図のような直角三角形なので\(\small \cos 90° =0\)より、(おまけ項)=0となり、余弦定理は、\(\small c^2=a^2+b^2\)、つまり三平方の定理になります(調節なしのため基準である直角三角形になっている)。
\(\small \angle C=0°\)と言われるとどんな状況かすぐには分からないので、図を描いてみます。無理やりCの角度を0にするためには、下図のように、点Aを辺BC上に持ってくるしかないので、もはや三角形ではなく一番下の図のような直線になります。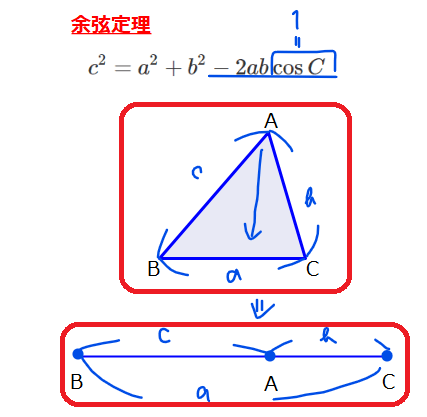
一方で余弦定理に\(\small \cos C=\cos 0°=1\)を代入して計算すると
$$
\begin{equation}
\begin{split}
&c^2=a^2+b^2-2ab\color{red}{\cos 0°}\\
&c^2=a^2+b^2-2ab\cdot \color{red}1\\
&c^2=a^2+b^2-2ab\\
&c^2=\color{red}{a^2-2ab+b^2}\\
&c^2=\color{red}{(a-b)^2}\\
&c=a-b\qquad (\small ∵ \space c>0)\\
\end{split}
\end{equation}
$$
最後に出てきた\(\small c=a-b\)は図を見れば一目瞭然ですが線の長さの関係性を表しています。
おまけ項がちょうど\(\small \color{red}{-2ab}\)になっていたことで、因数分解の公式が使えてすっきりと\(\small a-b\)の形が出てきていると考えると、コサインの係数の\(\small \color{red}{-2ab}\)も覚えやすいのではないかと思います。
このように、おまけ項\(\small \color{red}{-2ab}\)によって長さが調整されているわけです。
【図解的】余弦定理の覚え方
最後に、これまでの考察の結果を踏まえて冒頭に紹介した余弦定理の覚え方を見直してみましょう。
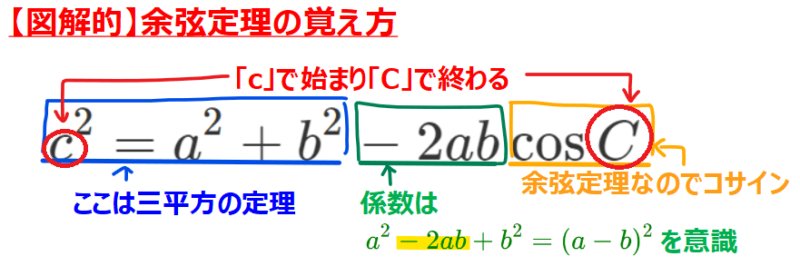
余弦定理の知識が身についた今であれば、それぞれの意味が理解できると思います。このような感じで長い公式でも分解してパーツごとに分けて覚えることで単純に暗記するよりも効率的に暗記できてかつ記憶にも残る(=忘れにくい)覚え方ができます。
まとめ
今回は余弦定理について詳しく解説しました。三平方の定理の一般形ということでおまけ項の意味や具体的なパターンで余弦定理がどう計算できるのか見てきました。三角比を使った図形問題を解く際によく使う公式なのでぜひ今回のポイントを復習して公式攻略してみてください!
余弦定理と合わせてよく使う公式である正弦定理の攻略法についても解説しているので、是非一緒に確認してみてください。
本日はここまでです。お疲れさまでした!