この記事では、絶対値を含む不等式の解き方について解説していきます。「普通の不等式は解けるけど、絶対値が入ると解けなくなる…」、「場合分けのやり方が分からない…」、「共通範囲なのか、合わせた範囲なのかが分からない…」と悩んでいる方向けに、これらの疑問を解説する記事になっているので、ぜひ最後までチェックしてみてください!
また、絶対値を含む不等式の解き方を理解するうえで絶対値を含む方程式の解法について知っておくとよりスムーズに理解できると思うので、あまり自信がない人やもう一度おさらいしておきたい人は、まずは「絶対値を含む方程式の解法」を確認しておきましょう。
1. 【解説編】絶対値を含む不等式の解法
では、早速ですが絶対値が入った不等式の解法手順を説明します。手順はシンプルで以下の3stepです。
では、それぞれについて詳しく説明していきます。
1.1 (絶対値の中身)=0で場合分けして絶対値を外す
これは、絶対値を含む方程式の時にも説明したポイントと同じになります。ここでは簡単なおさらいだけするので、もっと詳しく知りたい方は「絶対値を含む方程式の解法>絶対値の中身の正負で場合分け」を確認していただければと思います。
とにもかくにも、絶対値を含む式を解くには、絶対値を外すというステップから始まります。その際に絶対値をどのように外せばよいのかという方法が「(絶対値の中身)=0で場合分け」ということです。
たとえば、\(\small |x-3| > 1\)のような不等式があれば、絶対値の中身である「\(\small x-3\)」が「0」となる\(\small x\)、すなわち「3」を基準に\(\small x<3\)、\(\small 3≦x\)と場合分けすれば解けます。
他にも、絶対値が2つ含まれるような不等式、\(\small |x-1|-|x+2|<1\)のような場合でも、絶対値の中身が0になるポイント「1」と「-2」を境目にして、\(\small x<-2\)、\(\small -2≦x<1\)、\(\small 1≦x \)の3パターンに分けることで解いていけばokです。
個人的には、場合分けした範囲内で適当に数字を代入して絶対値の中身を確認しています。
先程例に挙げた\(\small |x-1|-|x+2|<1\)であれば、\(\small -2≦x<1\)の場合は、\(\small x\)が-2以上1未満の数字をなんでもいいから代入します。例えば計算しやすい0をそれぞれ代入してみると、\(\small x-1\)は-1で、\(\small x+2\)は2なので、\(\small |x-1|\)は中身が負なので\(\small -(x-1)\)(マイナスをつけて絶対値を外し)、\(\small |x+2|\)は中身が正なので\(\small x-1\)(そのまま絶対値を外す)のように判断しています。
え、でも今のは\(\small x=0\)の時を試しただけで、\(\small -2≦x<1\)の範囲の他の\(\small x\)を代入したら中身の正負が変わる可能性はないの?と不安に思った人は安心してください。同じ範囲内であれば、どんな値を入れても絶対値の中身の正負は変わりません。逆に変わらないからこそ、この範囲で場合分けしているわけです。
1.2 不等式を解いて場合分け範囲との共通範囲を求める
絶対値を外してしまえば、あとは不等式を解くだけですが、多くの人が陥りがちなミスがあります。それが「解いた後に共通範囲を求める」ことです。
たとえば、先程の\(\small |x-1|-|x+2|<1\)の不等式で、\(\small -2≦x<1\)の範囲で絶対値を外すと、\(\small -(x-1)-(x+2)<1\)なので、これを解いていくと
$$ -x+1-x-2 < 1$$
$$ -2x-1 < 1$$
$$ -2x < 2$$
$$ x > -1$$
となります。これで「\(\small x>-1\)がこの範囲の答えだ!」と思うのは時期尚早です。場合分けの範囲が\(\small -2≦x<1\)なので、この範囲と照らし合わせての範囲にしないといけないのです。つまり、場合分けした範囲と出てきた答えの共通範囲をとる必要があるのです。
なので、今回であれば、不等式を解いて出てきた\(\small x>-1\)と\(\small -2≦x<1\)を数直線上に図示して\(\small -1<x<1\)がこの範囲の答えとなるわけです。
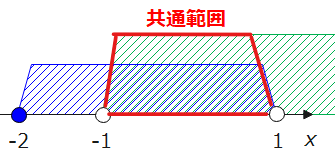
不等式を解いた後に場合分けした範囲との共通範囲を求めることを忘れないように注意しましょう!
1.3 合計範囲を求める
最後は、それぞれ場合分けして出てきた不等式の範囲を合計してあげれば答えになります。合計範囲が答えになる理由は、一言でいうと「それぞれの場合を合わせたものが全体になるから」です。わかったようなわからないようなって感じですね。。。
具体例として、たとえば「夏休みどこ行きたい?」と聞かれたとしましょう。頭の中で「観光メインだったら京都」、でも「海をメインにするなら沖縄」と2つの案が出たとします。であれば、最終的な答えとしては、「京都か沖縄」と2つの場合を合わせたものが答えになりますよね?
これと同じで、場合分けして出てきた不等式の答えも最終的には合計した範囲が答えになります。
2. 【演習編】絶対値を含む不等式を解いてみよう
2.1 絶対値を1つ含む(基本問題)
まずは絶対値の中身が0になる部分で場合分けして絶対値を外します。今回は、\(\small x=1\)が絶対値の中身が0になる分かれ目になるので、\(\small x<1\)、\(\small 1≦x\)の2つに場合分けして考えます。
(i)\(\small x<1\)の場合
絶対値の中身が負なので、マイナスをつけて絶対値を外して
$$-(x-1)>3x$$
$$-x+1>3x$$
$$-4x>-1$$
$$x<\frac{1}{4}$$
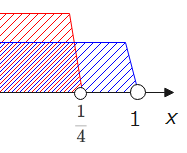
よって、場合分けの範囲との共通範囲を求めると\(\small x<\frac{1}{4} \cdots \)①
(ii)\(\small 1≦x\)の場合
絶対値の中身が正なので、絶対値はそのまま外せばよいので
$$x-1>3x$$
$$-2x>1$$
$$x<-\frac{1}{2}$$
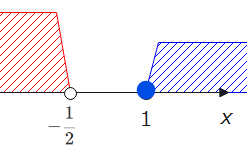
場合分けの範囲との共通範囲がないため、この場合は適切な解なし…②。
(i)、(ii)を合わせた範囲が答えなので、\(\small x<\frac{1}{4}\)。
理由は、その公式には、「\(\small c>0\)のとき」という前提条件が付いているからです(教科書をもう一度見てみましょう)。今回右辺の\(\small 3x\)は\(\small x\)が負になることもあるので、そもそも公式の前提を満たせていません。なのでこの公式は使えないのです。
このように高校ででてくる公式には「〇〇の場合」などの前提条件が付くことが多いので、公式を覚えるときには前提条件まで含めて覚えるようにしましょう。
2.2 絶対値を2つ含む(応用問題)
絶対値の中身が0になるのは、\(\small -2x+1=0\)→\(\small x=\frac{1}{2}\)、\(\small 3x+2=0\)→、\(\small x=-\frac{2}{3}\)。なので、今回は、\(\small x=-\frac{2}{3},\frac{1}{2}\)を境目として3パターンに場合分けします。
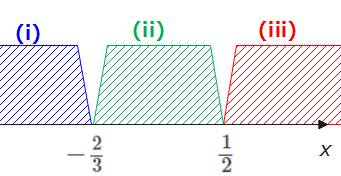
(i)\(\small x<-\frac{2}{3}\)の場合
この場合の絶対値の中身の符号を確認するために、たとえば\(\small x=-1\)を代入して確認すると「\(\small -2x+1\)」は3で正、「\(\small 3x+2\)」は-1で負であることが分かります。
よって、
$$(-2x+1)≦-(3x+2)$$
$$-2x+1≦-3x-2$$
$$x≦-3$$
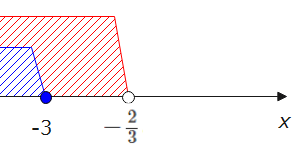
よって、場合分けの範囲との共通範囲は、\(\small x≦-3\)…①
(ii)\(\small -\frac{2}{3}≦x<\frac{1}{2}\)の場合
「\(\small -2x+1\)」正、「\(\small 3x+2\)」も正なので
$$-2x+1≦3x+2$$
$$-5x≦1$$
$$x≧-\frac{1}{5}$$
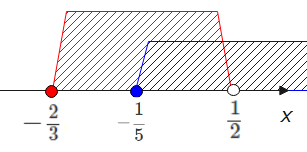
共通範囲を求めて、\(\small -\frac{1}{5}≦x<\frac{1}{2}\)…②
(iii)\(\small \frac{1}{2}≦x\)の場合
「\(\small -2x+1\)」負、「\(\small 3x+2\)」は正なので
$$-(2x+1)≦3x+2$$
$$-2x-1≦3x+2$$
$$-5x≦3$$
$$x≧-\frac{3}{5}$$
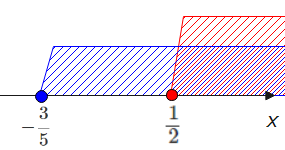
共通範囲を求めると、\(\small \frac{1}{2}≦x\)…③
①~③より、合計範囲は、\(\small x ≦-3,-\frac{1}{5}≦x \)。
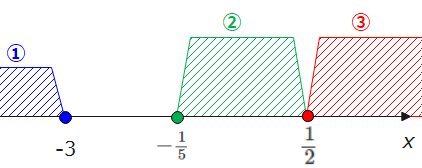
個人的なおすすめは、出てきた答えの近辺の値を問題の不等式に代入して不等式が成り立つかを確認することです。
今回の問題であれば、「\(\small x ≦-3\)」に対しては「\(\small x=-3.1\)」を代入して見ると(左辺)=\(\small |-2x+1|=7.2\)、(右辺)=\(\small |3x+2|=|-7.3|=7.3\)となり、\(\small |-2x+1|≦|3x+2|\)が確かに成り立っています。同じく、\(\small -\frac{1}{5}≦x \)についても「\(\small x=-0.1\)」を代入して見ると(左辺)=\(\small |-2x+1|=1.2\)、(右辺)=\(\small |3x+2|=1.7\)となり、やっぱり\(\small |-2x+1|≦|3x+2|\)が成り立っています。逆に、あえて「\(\small x=-0.3\)」など範囲外の値を代入して不等式が成り立たないことを確認するのもありです。
-3.1といった境目に近い値で確認する理由は、より正確に確認するためです。たとえば、「\(\small x ≦-3\)」の確認の時に「\(\small x = -10\)」みたいな-3からあまりにもかけ離れた値で確認すると、自分の答えが間違っていても不等式が成立してしまうことがあります。そういった可能性を排除するためになるべく近い値でテストするのがおすすめです。
3. まとめ
今回は、絶対値を含む不等式の解法について解説してきました。他のパターンの問題が来ても、今回の手順で考えることで解くことができると思うので、ぜひいろいろな問題にチャレンジしてみましょう!
また不等式関連の問題として、以下のような関連記事もありますので、気になった方はぜひこちらもチェックしてみてください!




コメント