この記事では、2次不等式の応用問題としてよく取り上げられる「不等式が常に成り立つ条件」の問題について解説します。「2次不等式は解けるけど、応用問題になるとどこから考えていけばいいかわからない…」、「考慮する条件が足りてなくて間違えることが多い…」、「条件ごとに出てきた不等式をどうまとめればよいのかわからない…」という悩みを抱えている人は、この記事で解法をまとめているので、ぜひ最後までチェックしてみてください!
また、そもそも2次不等式の解き方に自信がないという人は、「2次不等式の解き方」で解説しているので、初めにこちらを確認しておきましょう!
2次不等式の応用問題に共通する解き方のコツ
2次不等式の応用問題には結構たくさんのパターンがあり、パターンの多さが苦手意識を持ってしまう原因の一つになっていることも多いです。そんな数々の2次不等式の応用問題を私自身が解いてきた中で、多くの問題に共通する解き方のコツがあることに気づいたので、まずはそちらをお伝えします。
2次不等式の応用問題は、「軸の範囲、判別式、境界値の正負」の条件を考える!
「いろいろな問題があるのに割とシンプル!?」って驚いた人もいるんじゃないでしょうか?そうなんです。個人的な感覚として、このポイントさえ押さえておけばほとんどの問題は解けてしまいます。
では、それぞれどういう意味なのかを解説していきます。
軸の範囲の条件
2次関数の問題であれば、問題文の条件から軸の範囲に制約があるのかを考えます。
たとえば、問題文中に「2次関数が正の2つの実数解を持つ」という条件があれば、「軸>0」という条件が必要だとわかります。
軸の範囲については必ずしも条件があるわけではないので、特に条件がなさそうであれば飛ばしましょう。
判別式の条件
多くの問題では「この2次方程式が2つの実数解を持つとき…」や「2次関数が\(\small x \)軸との交点を持たないとき…」など解の個数についての条件が必ず書いてあります。なので、解の個数から判別式の条件を考えます。
ただ、問題によって解の個数が分かりにくく書いてあったりするので注意が必要です。たとえば、「2次関数と\(\small x \)軸との交点の個数」になっていたり、「2次不等式が常に成り立つ場合」という条件になっていたり。
判別式の条件のパターンをまとめてみたので、これに沿って考えるとよいでしょう!
・2次方程式が2つの実数解を持つとき
・2次関数が\(\small x\)軸と2つの交点を持つとき
・関数が2つの交点を持つとき
・2次方程式が1つの実数解を持つとき
・2次関数が\(\small x\)軸と接する(交点が1つ)とき
・関数が接する(1つの交点を持つ)とき
・2次方程式が実数解を持たないとき
・2次関数が\(\small x\)軸と交わらないとき
・すべての実数\(\small x\)に対して2次不等式が常に成り立つとき
一応補足として、\(\small D≧0\)というパターンもあって、これは\(\small D>0\)(解/交点の個数が2個の場合)と\(\small D=0\)(解/交点の個数が1個の場合)を組み合わせたものなので、単純に「2次方程式が解を持つ場合」や「2次関数が交点を持つ場合」などの条件が問題文に書かれた場合に使いましょう。
境界値の正負の条件
「境界値」という言葉が聞きなれないと思いますが、簡単に言うと「境界値とは範囲の端っこのこと」です。たとえば、「\(\small 1<x≦2\)」という範囲があれば、その境界値は「\(\small x=1\)」と「\(\small x=2\)」のことです。
「境界値の正負の条件を確認する」ということは、つまり、「範囲の端っこのプラスマイナスに条件があるかを確認する」ということです。なので、こちらも\(\small x\)の範囲に条件がなければ飛ばしてもokです。
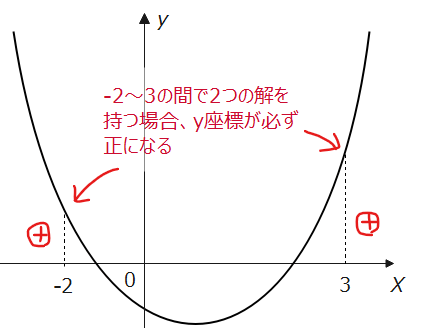
実際の問題では、「2次関数\(\small y=x^2+mx+1\)が\(\small -2<x<3\)の範囲で、異なる2つの実数解を持つとき」のような感じで出てきます。この場合は、グラフを描くとわかりますが、「\(\small x=-2\)」と「\(\small x=3\)」の\(\small y\)座標の正負を考えると必ず正になるという条件が出てきます。
2次不等式の応用問題の解法
前章で説明した解き方のコツを踏まえると、2次不等式の応用問題の解法は個人的に以下の手順がおすすめです。
・判別式の条件を確認
・境界値の正負の条件を確認
では、それぞれ簡単に説明していきます。
問題文に当てはまる2次関数のグラフを描く
これは、2次関数の問題を解くときには他の記事でもかなりしつこく言っていることではありますが、今回も図を描くことから始まります。「でも、2次方程式や2次不等式の問題だったら、2次関数じゃないからグラフは書かなくていいよね?」という質問をよく受けますが、初めのうちは描きましょう。グラフを描くことでイメージがわき、次のstep2の3つの条件が考えやすくなったり、パターンの考慮漏れを防げるメリットがあります。
3つの条件を調べる
ここは先程解き方のコツで述べた内容なので詳細は割愛して、ここでは3つの条件を調べる順番について触れておきます。
結論、「軸の範囲→判別式→境界値の正負」の順で調べていくのがよいと思います。理由は、「横で場合分けして縦で決める」ことができるから。どういうことか、この後具体的に説明しますね。
軸の範囲を考えることは、グラフがx軸のどのあたりにあるのかを考えることと同じです。軸の位置でグラフの左右の位置が決まるからです。軸の位置で場合分けすることが結構多いので、初めに考えるのがおすすめです。
次に、判別式で方程式の解やグラフの交点の個数ごとに問題文の条件を満たすかを考えます。x軸との交点はグラフの上下を決める要素になります。
最後に、境界値の正負は「xが〇〇の範囲で条件を満たす場合」などの制約がある場合に確認する条件です。なので、一番最後に考えるのがよいと思います。
よって、3つの条件は「軸の範囲→判別式→境界値の正負」の順で調べていくようにしましょう。
条件をまとめる
最後にstep2で求めた条件をまとめたものが答えになります。まとめる際には「共通範囲(AND条件)」なのか「合計範囲(OR条件)」なのかに注意しましょう。
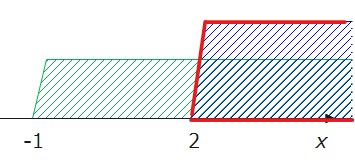
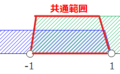
「共通範囲(AND条件)」とは、複数の条件すべてを同時に満たす範囲のことです。たとえば、\(\small -1<x\)(下図の緑)と\(\small 2<x\)(下図の青)の共通範囲であれば、緑と青の2つの範囲を同時に満たす赤で囲った範囲、\(\small 2<x\)が共通範囲になります。
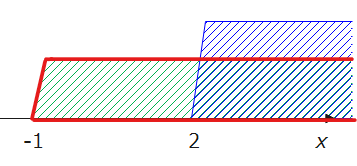
一方で、「合計範囲(OR条件)」とは、複数の条件のいずれかを満たす範囲のことです。上記と同じ例で合計範囲を考えるのであれば、答えは、赤枠で囲った範囲、\(\small -1<x\)になります。
step2で求める3つの条件は、問題文を満たすための条件なので、全部を満たさないといけないことから共通範囲で考えればokです。ただし、「〇〇の場合、××の場合」と場合分けをしているときは、それぞれの場合のいずれかを満たしていれば答えになるので、合計範囲でまとめることになります。
実際に問題を解いてみよう
では、実際にいくつかの問題を解いてみましょう。
不等式が常に成り立つ条件を求める
まずは、条件を満たすような\(\small x^2-kx-3k>0\)グラフを描いてみます。
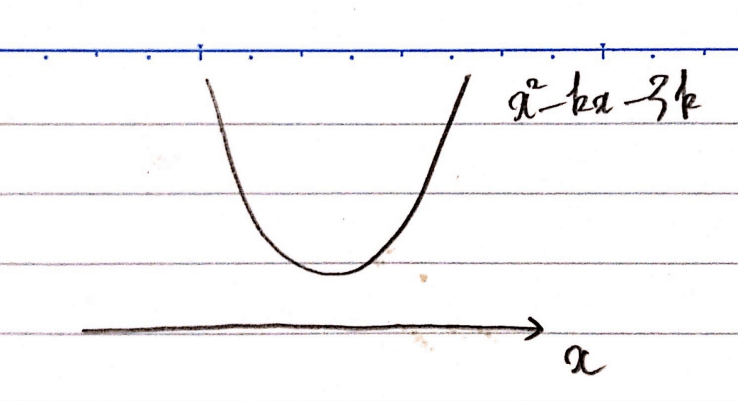
グラフはこのくらいの感じでokです。今回大事なのは、2次不等式がすべての\(\small x\)に対して正が成り立つということは、2次関数\(\small y=x^2-kx-3k\)を考えたときにどんな\(\small x\)であっても\(\small y>0\)となるということなので、\(\small x\)軸より上側に2次関数のグラフがあればよいという条件が分かるようにしておきます。
ではここから3つの条件「軸の範囲」、「判別式」、「境界値の正負」について確認していきましょう。
まず「軸の範囲」ですが、\(\small x\)軸と交わらければ左右の位置に制限はないので、特に条件はなしとなります。
次に判別式ですが、上のグラフから\(\small x\)軸と交わらないという条件は\(\small D<0\)なので
$$D=(-k)^2-4 \cdot 1 \cdot (-3k)<0$$
$$k^2+12k<0$$
$$k(k+12)<0$$
$$-12<k<0\quad\cdots①$$
「境界値の正負」は今回\(\small x\)の範囲について制限はないので特になしです。
最後の3つの条件をまとめるステップですが、今回は①の条件しかないので、答えは\(\small -12<k<0 \)となります。
ある区間内で不等式が成り立つ条件
3.1の問題と似ていますが、今回は\(\small x\)の範囲が限定されています。つまり、0~3以外であれば、問題の2次不等式が成り立っていなくてもokという点が相違点だということに気を付けて解いていきます。
まずは、問題文の条件に当てはまるグラフを描きます。
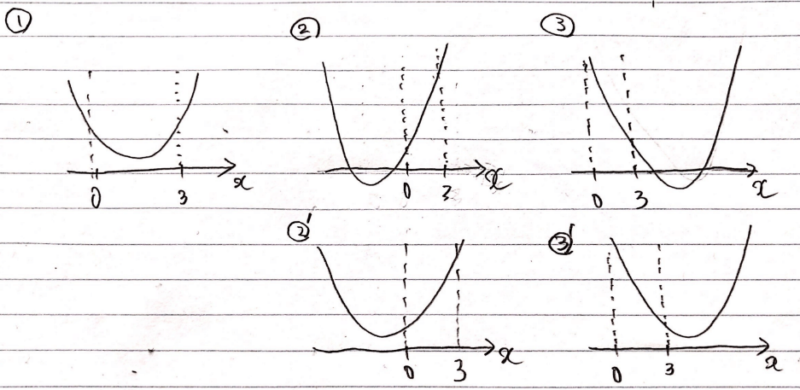
ポイントとしてはこの段階でなるべく多くのパターンを描いておくことが大切です。0~3の区間で\(\small x^2-2ax+a+2>0\)が成り立っていればよいだけなので、それ以外の区間では不等式が成り立っていなくてもよいことから、②や③のような図も描いておきます。
グラフを描くときに漏れが出てしまう人は、今回のポイント「判別式、軸、境界値の正負」のそれぞれのパターンで問題文の条件を満たすグラフが描けるかを確認するのがよいと思います。
例えば、今回の②のパターンは、「軸<0」縛りで図を描いていますが、②と②’は判別式のパターンと照らし合わせると、D=0(x軸と接する)のパターンもあります(下図参照)。
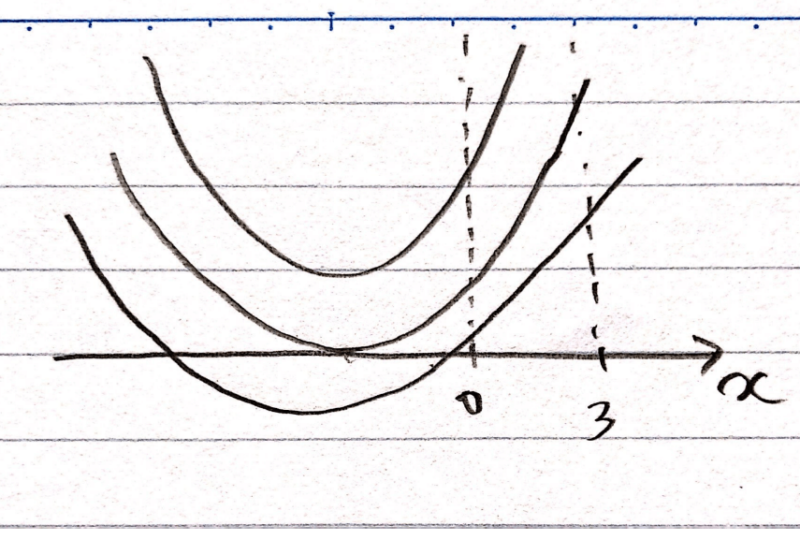
境界値(x=0,3)の正負で考えると、x=0や3でy座標が正になるパターンだけ書いてますが、逆に負になるパターンが考えられないか確認してみましょう。実際考えだしてみると、今回は問題文の条件を満たしつつ、x=0 or 3でy座標が負のグラフは描けないなと分かります。
慣れれば、大体パターンごとにこんな場合分けになるとすぐわかるようになりますが、初めのうちは、「判別式、軸、境界値の正負」の観点でグラフが描けるかをささっと確認するのがいいと思います。
では、軸の範囲の条件から確認します。①~③のグラフを見ると、①は「0≦軸≦3」、②,②’は「軸<0」、③,③’は「3<軸」なので、それぞれの場合ごとに「判別式」、「境界値の正負」も確認していきます。
その前に、公式を使って2次関数の軸を求めておくと\(\small x=a\)となるので、ここからは軸の範囲、すなわち\(\small a \)の範囲で場合分けしていきます。
(i)\(\small 0≦a≦3 \)の場合(①の場合)
判別式の条件は、\(\small D < 0\)なので、
$$\frac{D}{4}=a^2-(a+2)=a^2-a-2<0$$
$$(a+1)(a-2)<0$$
$$-1 < a < 2 \quad \cdots (1)$$
境界値の正負の条件は、\(\small x=0,3\)で\(\small y\)座標がいずれも正になるので\(\small f(x)=x^2-2ax+a+2\)とおくと、
$$f(0)=a+2>0 \quad ⇔ \quad a>-2$$
$$f(3)=9-6a+a+2>0 \quad ⇔ \quad -5a>-11 \quad ⇔ \quad a<\frac{11}{5} $$
よって、\(\small-2< a<\frac{11}{5} \cdots (2)\)。
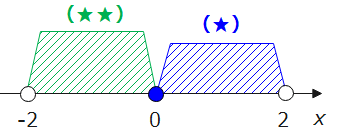
最後に条件をまとめます。今考えている範囲、\(\small 0≦a≦3 \cdots(3)\)とすると、(1)~(3)はどれも成り立たないと①のグラフにならないので、共通範囲を求めると\(\small 0≦ a < 2 \cdots (★)\)となります。
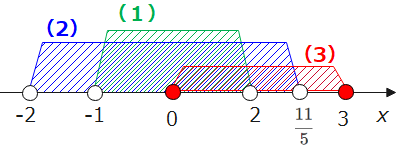
(ii)\(\small a<0\)の場合(②,②’の場合)
判別式は特に条件はなさそうです(x軸と交わっても交わらなくてもokなので)。次に、境界値の正負ですが、どの図でも\(\small x=0,3\)で\(\small y\)座標がいずれも正になるので、先程(i)で求めた結果から、\(\small a>-2 , a<\frac{11}{5} \)、つまり、\(\small-2< a<\frac{11}{5} \cdots (4)\)。
最後に、今考えている範囲を\(\small a<0 \cdots (5)\)として(4)、(5)の共通範囲を求めると、\(\small -2<a<0\cdots(★★)\)となります。
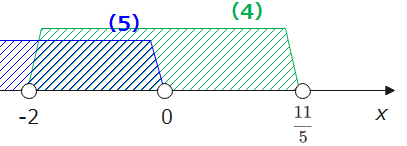
(iii)\(\small 3<a\)の場合(③,③’の場合)
(ii)と同様、判別式の条件なし、境界値の正負は、\(\small-2< a<\frac{11}{5} \cdots (6)\)です。よって、\(\small 3<a\cdots (7) \)として、(6)、(7)の共通範囲を見てみると、今回は共通部分がないので、該当範囲なし…(★★★)となります。
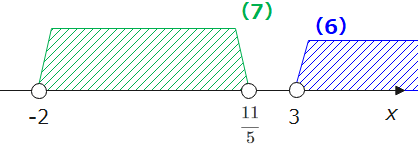
以上より、最終的な答えは、(i)~(iii)で場合分けしたそれぞれの条件(★~★★★)の合計範囲になる((i)~(iii)のどれかのパターンに当てはまっていれば問題文の条件を満たす)ので、\(\small -2<a<2\)となります。
まとめ
今回は、2次不等式の応用として、「不等式が常に成り立つ条件」、「2次関数の解の存在範囲」の問題について詳しく解説してみましたがいかがでしたでしょうか?モヤっとしていた解法が明確になって、「こんな手順で解いていけばいいんだ!」と思ってくれた人が1人でも増えてくれていたら嬉しいです。
今回紹介した問題は2次不等式の応用問題の一部なので、別の問題もこの考え方でどんどん解いて、学びを増やしていきましょう。
では、本日はここまでです。お疲れさまでした!







コメント