【3次方程式】裏ワザあり！？因数分解、因数定理、組立除法、係数比較を用いた解法のコツ

今回は3次方程式の解き方について、因数分解を利用した解法、因数定理を利用した解法、組立除法を利用した解法、係数比較を利用した解法の4つをそれぞれ解説していきます。

「具体的な解がなかなか見つからない…」、「組立除法よりもっと簡単に因数分解できる方法はないの？」と思ったことはないですか。おそらく、3次方程式を解いたことがある人なら誰もが一度は思ったことがある悩みや疑問だと思います。

本記事ではこのような悩みや疑問が解消できるように単なる解法の説明だけでなく、より早く簡単に3次方程式を解くためのコツや裏ワザ的解法についても解説していきたいと思いますので、是非最後までチェックしてみてください！

　本記事はこんな人におすすめ

3次方程式を解く際の4つの解法テクニック（因数分解、因数定理、組立除法、係数比較）について理解したい人
3次方程式を解く裏ワザ的解法を知りたい人
3次方程式の解を見つけるコツを知りたい人
定期テスト対策がしたい人

　本記事のレベル

重要度

低

余力あれば

普通

必須

高
難易度

易しい

易

やや易

やや難

難

難しい
暗記/理解

暗記重視

暗記

半々

理解

理解重視

【問題＆解説】3次方程式の解き方のコツ
本記事のまとめ

【問題＆解説】3次方程式の解き方のコツ

【問題1】因数分解を用いた解法（難易度：★☆☆）

次の3次方程式を解け。
（1）$\small 8x^3=1$
（2）$\small x^3-9x^2+27x-27=0$

問題解決のKey

3次方程式で因数分解の公式が使えるのは次の2パターン。
・$\small a^3x^3 \pm b^3=(ax\pm b)(a^2x^2 \mp abx+b^2)$.
・$\small a^3x^3 \pm 3a^2bx^2+ 3ab^2x\pm b^3=(ax\pm b)^3$.
⇒上記の公式に当てはまらない場合は、因数定理または組立除法など他の解法で解こう！

　解説（1）

左辺も右辺も3乗の形をしているので、因数分解の公式 $\small a^3x^3 – b^3=(ax- b)(a^2x^2 +abx+b^2)$が利用できる。

ゆえに、

\begin{split}
&\small 8x^3-1=0\\
\small \Leftrightarrow \space &\small (2x-1)(4x^2+2x+1)=0\\
\end{split}

よって、解は $\small 2x-1=0$ または $\small 4x^2+2x+1=0$を満たす [*1]。

*1：補足
3次方程式に限らず方程式を因数分解できた場合、『$\small AB=0$ ⇔ $\small A=0$または$\small B=0$』が成り立つことを利用する。
今回であれば、$\small A=2x-1, \space B=4x^2+2x+1$とみなせる。

それぞれの1次方程式及び2次方程式を解くと、

\begin{split}
&\small 2x-1=0\\
\small ∴ \space &\small \displaystyle x=\frac{1}{2}\\
\end{split}

\begin{split}
&\small 4x^2+2x+1=0\\
\small ∴ \space &\small \displaystyle x=\frac{-1\pm \sqrt{3}i}{4}\\
\end{split}

よって、答えは $\small \displaystyle \color{red}{x=\frac{1}{2} , \space \frac{-1\pm \sqrt{3}i}{4} \space \cdots 【答】}$.

　解説（2）

一見すると複雑そうな方程式に見えるが、最高次数の$\small x^3$と定数項の$\small -27=(-3)^3$がいずれも3乗になっていることから、因数分解の公式 $\small a^3x^3 -3a^2bx^2+ 3ab^2x- b^3=(ax- b)^3$が利用可能ではないかと推測できる。

実際に、上記の公式で$\small a=1, \space b=3$とおくと

$$\small x^3-9x^2+27x-27=(x-3)^3$$

となり、左辺が問題の方程式の左辺と一致することから、

\begin{split}
\small x^3- &\small 9x^2+27x-27=0\\
\small \Leftrightarrow \space &\small (x-3)^3=0\\
\small \Leftrightarrow \space &\small \color{red}{x=3 \space \cdots 【答】}\\
\end{split}

●補足
一般的に3次方程式は3つの解を持つが、今回のように解が1つの場合を3重解という。2次方程式でいう重解のようなパターンに該当する。

【問題2】因数定理・係数比較を用いた解法（難易度：★☆☆）

3次方程式 $\small x^3+2x^2-5x-6=0$を解け。

問題解決のKey

・3次方程式の王道的解法は、
　STEP1：因数定理を利用して因数を見つける
　STEP2：3次方程式を求めた因数で割り算
　STEP3：STEP2の除算で求まる2次方程式を解いて残りの解を求める
　　　　※3次方程式なので必ず1次式×2次式の形に因数分解できる
・STEP1の因数の見つけ方のコツについては問題4で解説。
・STEP2の割り算は筆算を用いた解法と組立除法を用いた解法が一般的だが、慣れてきたら係数比較しながら因数分解するのがおすすめ！詳細は本解答で解説する。
　組立除法を用いた解法については問題3で解説する。

Point：因数定理とは？

多項式 $\small P(x)$において $\small P(a)=0$が成り立つとき、多項式 $\small P(x)$は $\small x-a$を因数に持つ.
⇒ $\small x$に『ある数』を代入した結果が0になる場合、元の式は「 $\small x-$『ある数』」で割り切れる（＝因数分解できる）ということ[*1]。
＊因数とは、式を割り算したときに余りが０（割り切れる）になる式のこと。

*1：【補足】『割り切れる＝因数分解できる』とは？
この考え方を知っていると因数定理の応用問題も理解しやすくなるので絶対に理解しておきましょう。
割り切れるということと、因数分解できるということは同じことを意味しています。どういうことかというと、たとえば、10は2で割り切れます。これは$\small 10 = 2\cdot 5$と素因数分解できるからです。逆に、10を3で割ると割り切れずに余りが発生しますが、これは素因数分解した数の中に3がないからです。この考え方は数式の世界でも同様で、$\small x^2-4$は$\small x+2$で割り切れますが、これは$\small x^2-4=(x-2)(x+2)$と因数分解できるからです。言い方を変えると、割り切れる式 $\small (x+2)$を見つけられたらその式を含む形で因数分解ができることになります。
このように、『割り切れる』ということは『割り算した式を因数に持つ形で因数分解ができる』ということと同義なことが分かります。

≪具体例≫
2次式 $\small x^2+2x-3$は、$\small x=1$を代入すると $\small 1^2+2-3=\color{red}0$となることから、$\small \color{red}{(x-1)}$を因数に持つ形で因数分解ができる（割り切れる）ことが分かる。
実際に因数分解すると $\small x^2+2x-3=\color{red}{(x-1)}(x+3)$となり、$\small x-1$を因数に持つ形で因数分解できることが確認できる。

　解説

$\small x=-1$を代入すると

\begin{split}
&\small x^3+2x^2-5x-6\\
\small \Rightarrow \space &\small (-1)^3+2\cdot (-1)^2-5\cdot (-1)-6\\
\small = &\small -1+2+5-6\\
\small = &\small \color{#ef5350}0\\
\end{split}

より、因数定理から3次方程式 $\small x^3+2x^2-5x-6=0$は、$\small x+1$を因数に持つ。

よって、3次方程式の左辺 $\small x^3+2x^2-5x-6$を $\small x+1$で除算することで

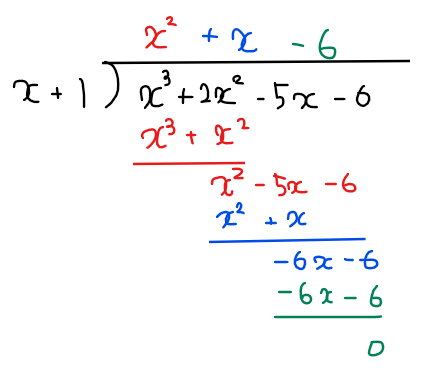
$$\small (x+1)(x^2+x-6)=0$$

のように因数分解できる。最後に括弧内の2次式もさらに因数分解することで

\begin{split}
&\small (x+1)(x^2+x-6)=0\\
\small \Leftrightarrow \space &\small (x+1)(x-2)(x+3)=0\\
\small ∴ \space &\small \color{red}{x=-1, \space 2, \space -3 \space \cdots 【答】}\\
\end{split}

【裏ワザ的解法】係数比較しながら因数分解する方法
はじめは難しくて抵抗感を感じる人も多いと思うが慣れれば簡単かつ爆速で解ける方法なので、是非マスターを目指そう！

この解法は因数定理を利用して$\small x+1$が因数であることを特定する部分までは解説と同様で、その後の割り算部分を爆速化する裏ワザになる。

●本問を例とした解法の解説
因数定理で$\small x-a$となるような因数が1つ見つかってしまえば、その因数を含む形で
$$\small (x-a)(px^2+qx+r)$$
の形に因数分解できることから、各係数$\small p,q,r$を3次方程式との係数比較によって決定することができる。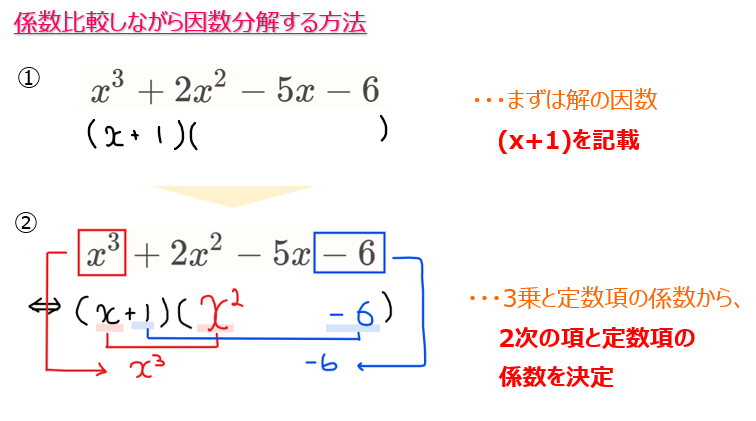

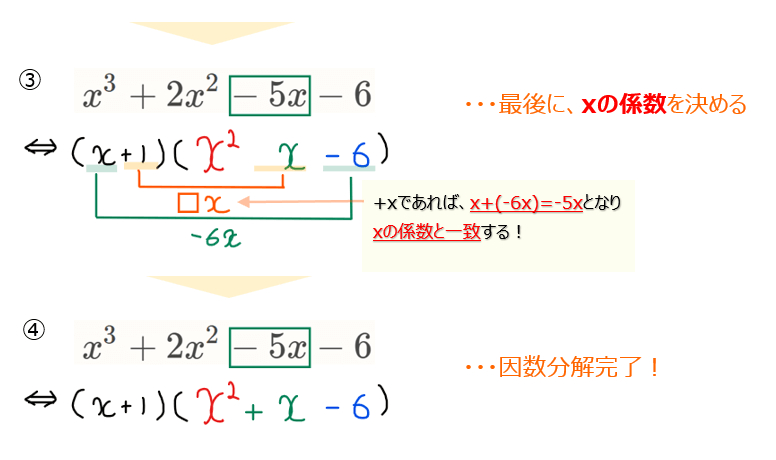
ポイントとしては係数決定していく順番で、すぐに決定できる$\small x^2$と定数項を求めた後で最後に$\small x$の係数決定を行う。
$\small x$の係数決定が少々難しいが、本問を例にすると②までで$\small (x+1)(x^2+qx-6)$の形までは決定しており、あとは係数$\small q$を求めたいわけなので、この式を展開したときの$\small x$の項だけを抜き出す（$\small (\color{green}x\color{magenta}{+1})(x^2+\color{magenta}{qx}\color{green}{-6})$で色付けした項同士のかけ算が$\small x$の係数になる）と$\small -6x+qx=(-6+q)x$になるので、あとはこの係数が3次方程式の$\small x$の係数である-5になることから、
\begin{split}
&\small -6+q=-5\\
\small ∴ \space &\small q=1\\
\end{split}
と求まる（慣れるとこの計算は文字$\small q$を置かなくてもできるようになるがはじめのうちは難しければ文字で置くのがおすすめ）。
以上より、$\small (x+1)(x^2+x-6)$と因数分解できる。

解法としては以上だが、最後に検算として求めた因数分解の式で $\small x^2$の係数を抜き出すと $\small 1\cdot x^2+x\cdot x=2x^2$となり3次方程式の$\small x^2$の係数とも一致することから合っていそうだという確認までできるとよいだろう。

【問題3】組立除法を用いた解法（難易度：★☆☆）

3次方程式 $\small x^3+4x^2+8x+5=0$を解け。

　解説

$\small x=-1$を代入すると

\begin{split}
&\small x^3+4x^2+8x+5\\
\small \Rightarrow \space &\small (-1)^3+4\cdot (-1)^2+8\cdot (-1)+5\\
&\small =-1+4-8+5\\
&\small =0\\
\end{split}

となることから、因数定理より $\small x^3+4x^2+8x+5$は $\small (x+1)$を含む形で因数分解できる。問題2ではここから筆算することで因数分解したが、ここでは組立除法を用いて因数分解を行う。

Point：組立除法のメリット

因数分解は筆算よりも組立除法を活用することで、素早くかつ機械的に解くことができる。

STEP

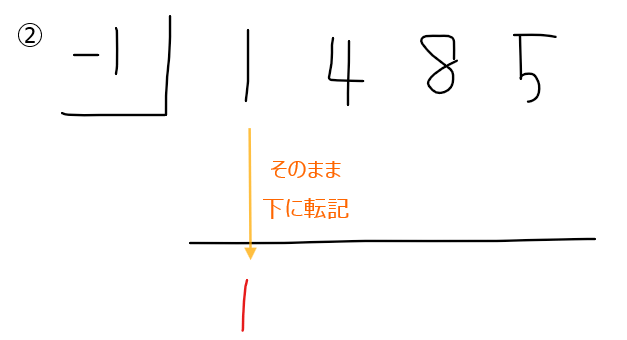
3次方程式の係数を一列に書き、左端に因数定理で見つけた解を記載。

STEP

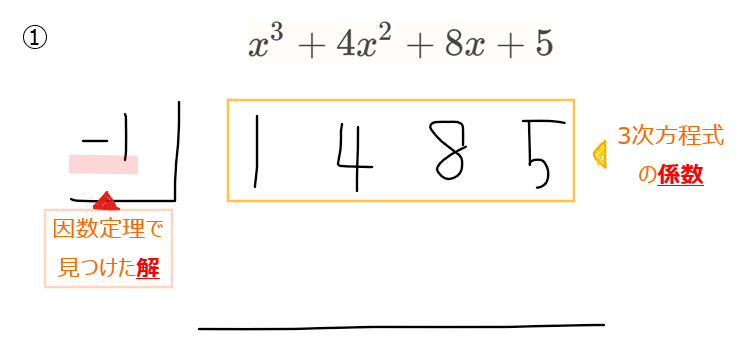
一番左端の数字（今回であれば1）をそのまま下に転記。

STEP

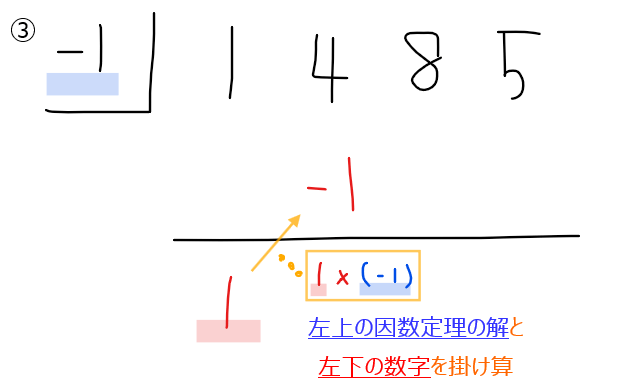
転記した数字に因数定理の解を掛け算した数を右斜め上に記載（下図参照）。

STEP

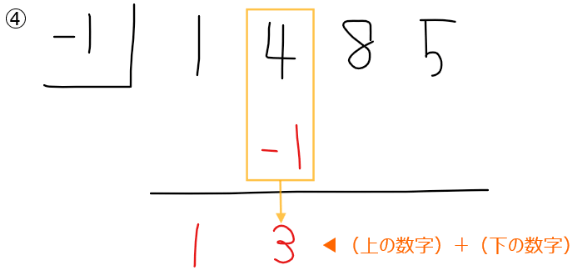
上の数字と下の数字を足し算した数字を記載。

STEP

以降は、STEP3の因数定理の解の掛け算とSTEP4の足し算を繰り返し行い、最終的な足し算の結果が「０」になったら組立除法完了となる。

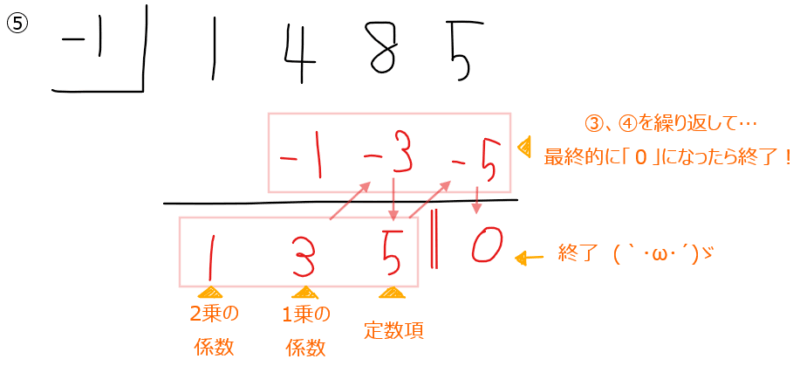
結果として最下段に現れた「1, 3, 5」の数字を順番に$\small x^2$の係数、$\small x$の係数、定数項とした2次式 $\small x^2+3x+5$が因数分解後の2次式となる。

よって、問題の3次方程式は

\begin{split}
&\small x^3+4x^2+8x+5=0\\
\small \Leftrightarrow \space &\small (x+1)(x^2+3x+5)=0\\
\end{split}

のように因数分解できる。よって、3次方程式の解は、$\small x+1=0$ または $\small x^2+3x+5=0$を満たす。

よって、求める解は $\small \displaystyle \color{red}{x=-1, \space \frac{-3\pm \sqrt{11}i}{2}\space \cdots 【答】}$.

●別解：係数比較しながら因数分解
裏ワザ的解法として紹介した係数比較しながら因数分解する方法についても参考として載せておく。
$\small x=-1$が解の一つであることから、$\small x+1$を含む形で因数分解可能。
$\small x^3$の係数1と定数項 5の値に注目することで、
$$\small x^3+4x^2+8x+5 =(x+1)(\color{#ef5350}{x^2}+■x+\color{#ef5350}5)$$
のように$\small x^2$の項と定数項の係数が確定する。最後に、$\small x$の項の係数に着目することで、$\small 5x+■x=8x$となればよいことから $\small ■=3$と求まるので、$\small (x+1)(x^2+\color{#ef5350}3x+5)$と因数分解できる。

【問題4】有理数解が見つけにくい3次方程式の解法（難易度：★★☆）

3次方程式 $\small 2x^3-5x^2+x+3=0$を解け。

問題解決のKey

3次方程式の有理数解の候補は、$\small \displaystyle \color{#ef5350}{\pm \frac{\mathsf{定数項の約数のどれか}}{\mathsf{最高次数の係数の約数のどれか}}}$を利用して絞り込め！

●補足：解の候補を絞り込める理由
3次方程式を解くにあたっては因数分解のために適当な解を1つ見つける必要があるが、一般的に解を見つけることは容易ではない。しかし、問題解決のKeyに記載した方法で解の候補をある程度特定することが可能である。この方法で解の選定ができることは次のように説明できる。

仮に3次方程式が $\small (ax+b)(cx^2+dx+e)=0$と因数分解できるとすると、有理数解の一つは$\small \displaystyle x=-\frac{b}{a}$になる（$\small cx^2+dx+e=0$の解は一般に無理数解（ルートを含んだ解）になるが、$\small ax+b=0$は1次式なので必ず有理数解になる）。このとき、もとの3次方程式は
$$\small acx^3+(bc+ad)x^2+(ae+bd)x+be=0$$
となるため、係数の形がシンプルな$\small x^3$（最高次数）の係数と定数項に着目すると、見つけ出したい有理数解$\small x=-b/a$の分母の値 $\small a$は $\small x^3$の係数が$\small ac$であることから、$\small x^3$（最高次数）の係数の約数のどれかに絞られる。同様に、有理数解の分子の値 $\small b$は定数項が $\small be$であることから、定数項の約数のどれかに絞られる。

以上の理由から、解の候補は$\small \displaystyle \color{#ef5350}{\pm \frac{\mathsf{定数項の約数のどれか}}{\mathsf{最高次数の係数の約数のどれか}}}$と考えることができる。先頭の$\small \pm$は、分母と分子の約数の正負の組合せによってプラスの値にもマイナスの値にもなり得る可能性があるというだけなので、符号は最後に調整すればよいだろう。

【具体例】有理数解の特定方法
たとえば、問題2の3次方程式 $\small x^3+2x^2-5x-6=0$の有理数解を特定する例で考えよう。
まず最高次数の係数は1なので、約数は$\small 1$のみであることから有理数解の分母は1と確定できる。次に、定数項は$\small -6$なので、約数は$\small \pm 1,\pm 2,\pm 3,\pm 6$の8パターン[*1]に絞り込みができる。
よって、解の候補としては
$$\small \displaystyle \pm \frac{\mathsf{定数項の約数のどれか}}{\mathsf{最高次数の係数の約数のどれか}}=\pm 1,\pm 2,\pm 3,\pm 6$$
の8つのいずれかに絞ることができるので、後は小さい順に確認していけばよい。

*1:【補足】約数が8パターンになる理由
「補足：解の候補を絞り込める理由」での解説を踏まえると、今回は定数項が $\small be = -6$なので、$\small b,e$の組合せとしては
\begin{split}
\small (b,e) = &\small (1,-6),(2,-3),(3,-2),(6,-1),\\
&\small (-1,6),(-2,3),(-3,2),(-6,1)
\end{split}
の8パターンなので、有理数解の分子 $\small b$の値の候補は
$$\small b=\pm 1,\pm 2,\pm 3,\pm 6$$
になる。

　解説

因数分解するためにまず適当に1つ解を見つける必要があるが、大概の問題は $\small x=\pm1, \pm2$あたりを代入すれば0になる解を見つけことができるのだが、本問は適当な値の代入ではなかなか見つけることができない。

問題解決のKeyでも記載したが、闇雲に値を代入するのではなく解の候補の中から計算しやすい順などで解を探していく方が効率的だろう。

本問の場合、$\small x^3$の係数が2、定数項が3なので解の候補は、分母の候補が$\small 1,2$、分子の候補が$\small 1,2,3$の組合せになるので

\begin{split}
\small \displaystyle \pm \frac{\mathsf{定数項の約数のどれか}}{\mathsf{最高次数の係数の約数のどれか}}= &\small \pm 1, \pm 2, \pm 3,\\
&\small \displaystyle \pm \frac{1}{2}, \pm \frac{3}{2} \quad [*1]\\
\end{split}

*1：【補足】解の候補数について
分母の候補が$\small 1,2$、分子の候補が$\small 1,2,3$なので単純な組合せ数は6通り（$\small \pm$ の符号も含めると12通り）になるが、実際には分母・分子共に2の場合は $\small \displaystyle \frac{2}{2}=1$となり分母・分子共に1の場合と同じ解になるといったように重複するものもある。

あとは解の候補を一つずつ代入して確認していくと、$\small \displaystyle x=\frac{3}{2}$のとき

\begin{split}
&\small 2x^3-5x^2+x+3\\
\small \Rightarrow \space & \small \displaystyle 2\cdot \left(\frac{3}{2}\right)^3-5\cdot \left(\frac{3}{2}\right)^2+\frac{3}{2}+3\\
& \small =\displaystyle \frac{27}{4}-\frac{45}{4}+\frac{6}{4}+\frac{12}{4}\\
& \small =\color{#ef5350}0\\
\end{split}

となり、$\small \displaystyle x=\frac{3}{2}$が有理数解であることが分かる。

よって、因数定理より 3次方程式 $\small x^3-5x^2+x+3$は $\small 2x-3$を因数に持つ [*2]。

*2：分数解の因数の求め方
$\small x=2$が解の場合などは無意識的に「$\small x-2$を因数に持つ」と求められても、今回のように分数になると意外と因数の求め方が分からなかったりするので補足する。
因数の求め方は、「$\small xの式 =\color{red}0$」の形に変形した際の「$\small x$の式」部分が因数になる（方程式を逆に解いていくイメージ）。
先程の $\small x=2$が解の場合であれば、右辺の2を左辺に移項すると $\small x-2=\color{red}0$の形となり、確かに左辺が因数 $\small x-2$になっていることが分かるだろう。
同様に分数の場合も考えると、本問であれば、
\begin{split}
&\small \displaystyle x=\frac{3}{2}\\
\small \Leftrightarrow \space &\small \displaystyle 2x=3\\
\small \Leftrightarrow \space &\small \displaystyle 2x-3=0\\
\end{split}
となるので、$\small 2x-3$が因数になる。

よって、問題の3次方程式は $\small 2x-3$を因数に持つ形で因数分解できるので

\begin{split}
&\small 2x^3-5x^2+x+3=0\\
\small \Leftrightarrow \space &\small (2x-3)(x^2-x-1)=0 \quad [*3]\\
\end{split}

*3：【補足】種々の因数分解方法について
①筆算による解法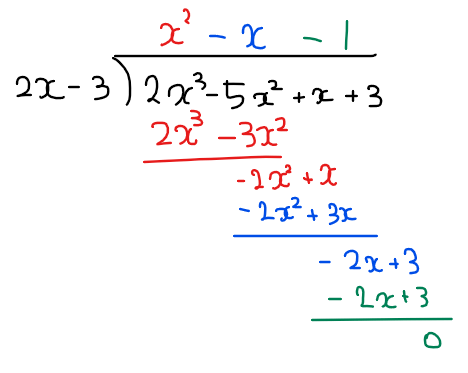

②組立除法による解法
組立除法は基本的には因数が$\small x-a$型の場合でしか使えない…。
今回は因数が$\small 2x-3$であり$\small x$の係数が1ではないため直接的には組立除法は使えないが、因数を$\small \displaystyle x-\frac{3}{2}$として考えれば組立除法が使える。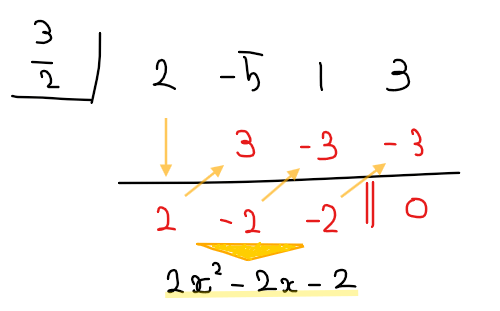

ここから、$\small \displaystyle \left(x-\frac{3}{2}\right)\color{#ef5350}{(2x^2-2x-2)}=0$と因数分解できることが分かったので、
\begin{split}
&\small 2x^3-5x^2+x+3=0\\
\small \Leftrightarrow \space &\small \displaystyle \left(x-\frac{3}{2}\right)(2x^2-2x-2)=0 \\
\small \Leftrightarrow \space &\small \displaystyle \left(x-\frac{3}{2}\right) \times 2 (x^2-x-1)=0 \\
\small \Leftrightarrow \space &\small \displaystyle (2x-3)(x^2-x-1)=0 \\
\end{split}
このように、分数解の場合、組立除法は1クッション式変形の手間が必要になる。

③係数比較による解法（おすすめ！）
\begin{split}
&\small 2x^3-5x^2+x+3=0\\
\small \Leftrightarrow \space &\small (2x-3)(\color{#ef5350}{x^2}+■x\color{#ef5350}{-1})=0 \\
\end{split}
$\small x$の係数は、
\begin{split}
\small -2x-3■x &\small =x\\
\small \Leftrightarrow \space -3■x &\small=3x\\
\small ∴ \space ■ \space &\small=-1\\
\end{split}
よって、$\small (2x-3)(x^2-x-1)=0$.

[*3]より、$\small 2x-3=0$ または $\small x^2-x-1=0$であり

\begin{split}
&\small x^2-x-1=0\\
\small ∴ \space &\small \displaystyle x=\frac{1\pm\sqrt{5}}{2}\\
\end{split}

よって、求める解は、$\small \displaystyle \color{red}{x=\frac{3}{2}, \space \frac{1\pm\sqrt{5}}{2} \space \cdots 【答】}$.

本記事のまとめ

今回は3次方程式の解の求め方について代表的な3つの方法である因数分解を用いた解法、因数定理を用いた解法、組立除法を用いた解法について徹底解説してみました。

今回解説した解き方のコツは3次方程式だけではなく高次方程式（3次方程式以上の方程式）を解く際にも基礎となる考え方になるので、しっかり復習して解き方を身に着けてしまいましょう。

今回解説した内容を基礎知識とした3次方程式に関する標準問題については、こちらの記事「3次方程式】1の3乗根ωを利用した式の値、解の条件による係数決定（実数解・虚数解、重解）」で解説していますので、よければ併せて確認してみましょう。

最後に、解き方のコツをまとめて終わりとしましょう。

☆重要Point☆
・3次方程式の主な解法は…
　①因数分解を利用して解く
　　＊使える公式は2つだけ。一般的には②が主流。
　②因数定理を利用して解く
　　＊解の候補は$\small \displaystyle \pm \frac{\mathsf{定数項の約数のどれか}}{\mathsf{最高次数の係数の約数のどれか}}$で絞る
　　＊因数分解は「筆算」、「組立除法」または「係数比較」で分解
　　　→係数比較がどんな問題でも素早く解けるのでおすすめ！