本記事は数学オリンピック2024年予選問題の面白い問題を解説する記事の第2弾です。前回記事が気になる方は、「【数学オリンピック】n+2024、n-34の各桁が素数になる3桁の整数nを求めよ(予選問題(2024))」をぜひ確認してみてください!
個人的には数学オリンピックに出題される問題は、受験数学とはまた違った頭の使い方や数学的センス・勘的なものが求められる気がしているので、いろいろな問題を解いて数学の面白さを感じていければと思っています。
また、最後の方の問題は数オリ受験者のような数学の猛者たちが集まった中でも正答率が圧倒的に低いようなので、正直私に解ける気はしませんが、どのレベルまで解くことができるのかも併せて検証していきたいと思いますので、皆さんも一緒にどこまで解けるのかぜひチャレンジしてみてください!
【数学オリンピック】予選問題(2024年)
【問題】黒石と白石を並べ多い色に置き換える問題
\(\small n\)を0以上\(\small 5^5\)以下の整数とする。黒石\(\small n\)個と白石\(\small 5^5-n\)個を横一列に並べ、次の操作を5回繰り返す。
石の列を左から順に5個ずつの組にする。各組に対して、その組に属する5個の石を、それらの5個の石のうち多い方の色の石1個に置き換える。
最初の石の並べ方によらず、最後に残る1個の石が必ず黒色であるような\(\small n\)としてありうる最小の値を求めよ。
【解説】解答までの思考法を分かりやすく解説
まず問題設定の意図を把握することからはじめます。問題文の操作を黒石10個、白石5個の場合の具体例で確認してみましょう(一旦\(\small 5^5\)個の石があるとかは数がデカすぎるので無視!)。
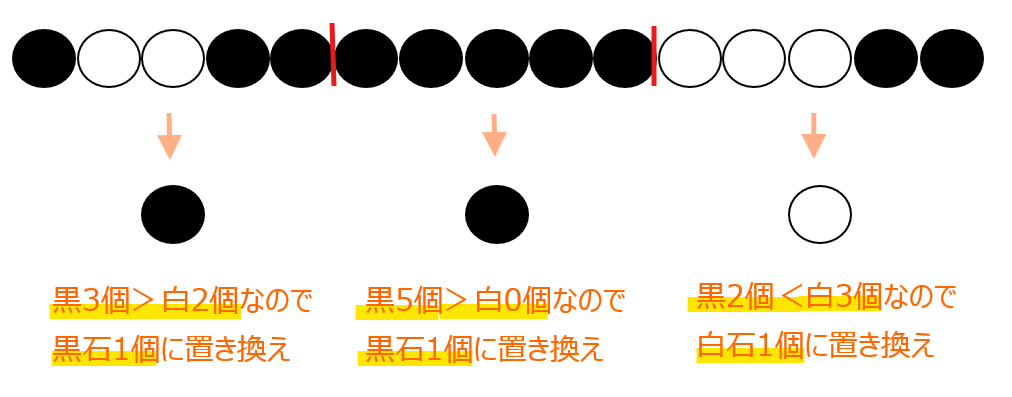
上図のような並びだった場合、各組で多い色の石1個に置き換えていくという操作を5回繰り返すというわけです。そして、1回の操作が終わるともともとあった石の個数が1/5倍になっていくので、問題の最初の石の個数が\(\small 5^5\)個とバカでかかった理由は、5回の操作後に最終的に石の個数が1個になるためだったというわけです。
●余談
国語力のない私は、はじめこの問題の操作を、『各組の5個の石すべてを多い方の石の色に置き換える』だと勘違いし石の個数が減らない中で最後に黒石1個だけが絶対に残るパターンを考える問題…だと盛大に勘違い(^^;)。数学オリンピックの問題にビビり散らかしてまともに問題も理解できない精神状態でしたが、途中で誤解に気が付き何とか軌道修正しました。
さて、問題のイメージがついたところで早速本題に入っていきたいのですが、この問題のポイントは言うまでもなく『最初の並べ方によらずに最後に必ず黒石が残る』という点です。
なので、ゴールの形からなるべく黒石の個数が少なくなるような一手前の配置を逆算することで黒石の個数\(\small n\)の最小値が求められそうです。このゴールから逆算して考えるという思考法がこの問題の1つ目の関門です。
では逆算していきましょう。
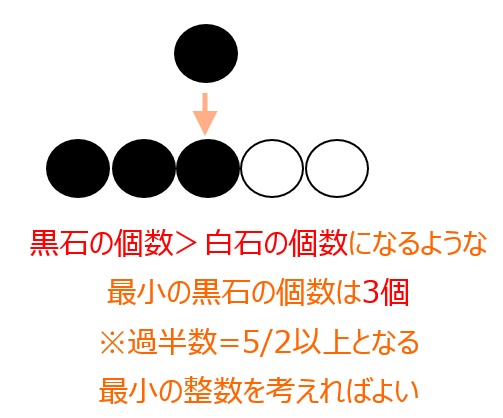
まずは4回目の操作終了時点の並びは上図のようになっている必要がありますね。
次の3回目の操作終了時点がちょっと山場あり!?という感じです。3回目終了時点の並びも短絡的に考えると『黒石は「黒:3、白:2」にして、白石は極力黒石を使わないように「黒:0、白:5」と置き換えすれば、いけるのでは?』という発想が思いつきます。
では実際にこの考え方が正しそうかを実験してみたのが下図になります。
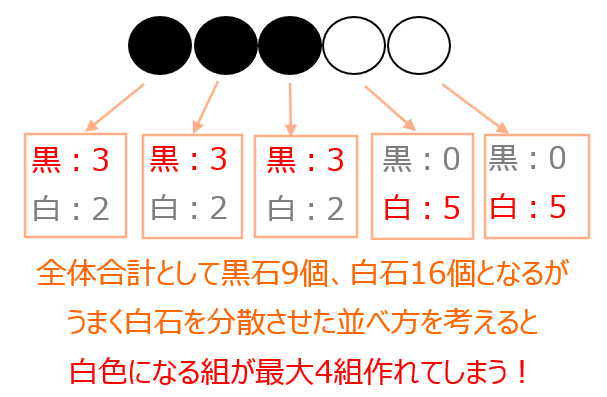
結論、この置き換えだと白石が多すぎるため、うまく白石を各組に分散させる並べ方を考えた場合、各組に含まれる黒石と白石の個数を(黒石の個数,白石の個数)で表すとすると(黒5,白0)、(黒2,白3)、(黒2,白3)、(黒0,白5)、(黒0,白5)のように、白石になる組が4組も作れてしまいます!
ではどこがまずかったのかというと、列の左端にある(黒3,白2)の白石2個が別の(黒3,白2)ペアへ1個ずつ移動することで、白石の数が(黒:3,白:2)→(黒:2,白:3)になるという下克上がおきてしまったワケです。

また、今度は右側にある(黒0,白5)の2組に着目してみましょう。
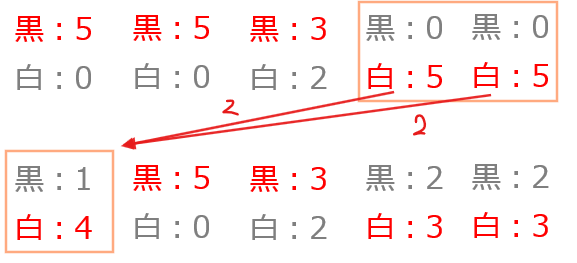
このように右側にある(黒0,白5)の2組についても、左側にある(黒5,白0)ペアに白石を2個ずつ移動させることで、(黒5,白0)→(黒1,白4)になり、白色になる組が3組できてしまいます。
ここからわかることは、『1組を黒石へ変換するためには組内に黒石は最低3個必要だが、(黒3,白2)の組を作りすぎるのもダメ(下剋上がおきてしまう)』、『白石に変換される組も黒石の節約のために安易に(黒0,白5)とすると他組への移動によって白色になる組ができてしまう可能性がある』ということ。
では最適なバランスがどこにあるのかを考えてみます。これは考えてみると意外とシンプルで左側3組の中に白石が3つあると、その3つを1組に集約させることで(黒2,白3)のペアが作れてしまうため、白石の個数は最大2個にする必要があります。また、右側の2組については、白石が移動されて他組で黒白の個数の優劣の逆転が起きると困るので白石の個数は最大3個(白石を移動させると移動元の組の白石の個数が2個以下になり白へ変換できなくなる)、すなわち黒石を最低2個は持たせておく必要があります。
このことを考慮するとペアの組合せは以下の場合に限られます。
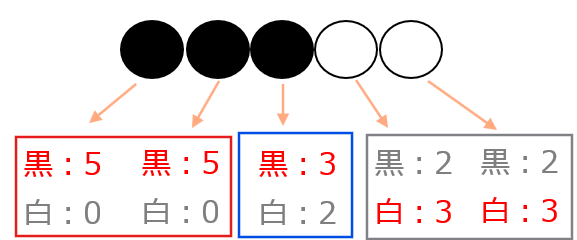
ここからわかったことをまとめると1手前への変換は以下のルールに則り置き換えればよいことが分かります。
●変換規則
【①】左側の領域(上図赤枠)が「黒石の個数-1」組、【②】中央の領域(上図青枠)が1組、【③】右側の領域(上図グレー枠)が「白石の個数」組あり、それぞれの組にある黒石・白石の個数は
【①】左側の領域:(黒5,白0)
【②】中央の領域:(黒3,白2)
【③】右側の領域:(黒2,白3)
のように変換するのが黒石が最も少なくなる。
よって、あとはこの変換規則に則り初手の黒石の個数を求めていきましょう。
[5回目終了時点]
黒石の個数=1個
白石の個数=0個
[4回目終了時点]
黒石の個数=3個
白石の個数=2個
[3回目終了時点]
黒石が3個、白石が2個なので、変換規則から【①】が2組、【②】が1組、
【③】が2組になればよいので
黒石の個数=5×2(【①】にある黒石の個数)+3×1(【②】にある黒石の個数)
+2×2(【③】にある黒石の個数)=17個
白石の個数=2×1(【②】にある白石の個数)+3×2(【③】にある白石の個数)=8個
[2回目終了時点]
黒石が17個、白石が8個なので、【①】が16組、【②】が1組、【③】が8組になればよいので
黒石の個数=5×16(【①】にある黒石の個数)+3×1(【②】にある黒石の個数)
+2×8=99個
白石の個数=2×1(【②】にある白石の個数)+3×8(【③】にある白石の個数)=26個
[1回目終了時点]
黒石が99個、白石が26個なので、【①】が98組、【②】が1組、【③】が26組あることになるので
黒石の個数=5×98(【①】にある黒石の個数)+3×1(【②】にある黒石の個数)
+2×26(【③】にある黒石の個数)=545個
白石の個数=2×1(【②】にある白石の個数)+3×26(【③】にある白石の個数)=80個
最後に、開始時点の黒石の個数は、1回目終了時点の黒石の個数が545個、白石の個数が80個であることから、
黒色の個数=5×544(【①】にある黒石の個数)+3×1(【②】にある黒石の個数)
+2×80(【③】にある黒石の個数)=2883個…【答】
【別解】スマートな解答
解説で紹介した解き方は私の解き方でしたが、数学の天才はもっとスマートな解法で解いているようなので、ここからはその解き方を紹介します。数オリの後半問題に立ち向かうにはこの考え方が呼吸するようにできないとダメなのかも…。
この解法のポイントをはじめに伝えておくと、『白石が何個あるとアウトになるか』を考えることです。たとえば、最後に黒石が1個残るためには(黒3,白2)である必要があると説明しましたが、逆を言えば白が3個あるとアウトなワケです。
白色になる組が3組あるとアウトということは、もう一手前の手では、白石が9個あるとアウトであることが分かります(各組に3個ずつ白石を分配することで白石3個に置き換えることができてしまうため)。
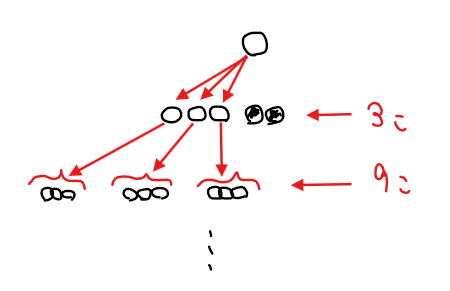
このように考えると、アウトな白石の個数は\(\small 3\)のべき乗で増えていくことが分かるので、5手前の最初の状態では\(\small 3^5=243\)個あると最終的に白石1個が残ってしまうワケです。
逆に言えば、この状態から白石が1個でも減れば白石になる組を黒石に逆転できることになるため、最終的に黒石1個が残ることになります。よって、白石が242個の状態が黒石が最も少ない個数の状態となります。
よって、黒石の個数は\(\small 5^5-242=2883\)個…【答】と求まります。
本記事のまとめ
今回は黒石と白石を一列に並べ多い色の石に置き換える問題について解説してきましたが、いかがだったでしょうか?
私の解答のように、実験的にいくつか試してみて規則性を見つけることで計算するもよし、条件を満たさない場合の条件を見つけてスマートに計算するもよし。いずれにしても、この問題を解く際に実際に具体的な計算をしてみて規則性を探し当てることがポイントになります。
・筋の良い規則性を見つけるときれいに解くことができる(これが難しい…)。
今回は以上です。お疲れさまでした!







コメント