今回は円のベクトル方程式を使った問題を分かりやすく解説していきます。ベクトルでは頻出の「点Pはどのような図形を描くか?」というパターンの問題です。苦手な人は解き方のコツを徹底解説しているのでこの記事を読んで解消していきましょう!「自分は大丈夫!」という人も、しっかり解けるか確認するために問題にチャレンジしてみてください!
- 解き方の指針ってどう考えればいいの?
- 円のベクトル方程式の暗記のコツってないの?
- 「どんな図形か?」って聞かれて数式をどのように日本語化すればいい?
【基礎講義】円のベクトル方程式とは
【円のベクトル方程式】2種類の基本形
\(\small xy\)平面上で円上の点を表そうと思ったら \(\small x^2+y^2=r^2\)と表せるように、ベクトルを使って円上の点を表すことができます。ではベクトルを使って円上の点をどのように表せるのかについてここでは解説します。
さっそくですが、結論、以下のようにあらわすことができます。
■円のベクトル方程式の基本形2パターン
・基本形①:半径に着目した関係式
原点をOとして円周上の点をP、円の中心をC、半径を\(\small r\)とする円は、
\begin{equation}
\small \color{red}{|\mathrm{\overrightarrow{OP}- \overrightarrow{OC}} |=r }
\end{equation}
・基本形②:直径の円周角は90°に着目した関係式
円周上の点をP、直径を線分ABとする円は
\begin{equation}
\small \color{red}{\mathrm{\overrightarrow{AP}\cdot\overrightarrow{BP}}=0}
\end{equation}
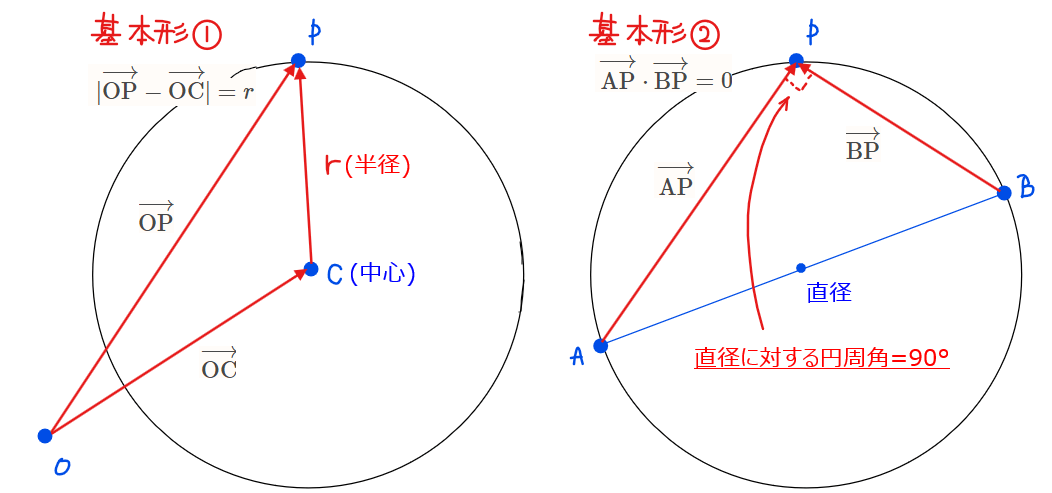
円をベクトルを使って表そうと思ったら2パターンの表し方があるということをまずは覚えておきましょう。では、この2通りのどちらを使えばよいのか?という疑問に対しての答えとしては、「問題で与えられた条件から使えそうな方を選んで使う」となります。実際にこの後の演習問題を解けば分かりますが、多くの場合は、【ベクトルの和】であれば【基本形①】、【内積】であれば【基本形②】といった感じになりますが、あまり覚える必要はないです。式変形をしていく中で自然と分かってきます。
【問題&解説】円のベクトル方程式と軌跡
【問題1】円のベクトル方程式の基本問題
平面上において、同じ直線上にない異なる3点\(\small \mathrm{A,B,C}\)に対し、等式 $$\small \mathrm{\overrightarrow{AB}\cdot\overrightarrow{AC}+\overrightarrow{AP}\cdot\overrightarrow{AP}=\overrightarrow{AB}\cdot\overrightarrow{AP}+\overrightarrow{AC}\cdot\overrightarrow{AP}}$$ を満たす点\(\small \mathrm{P}\)はどのような図形を描くか。 [類 鳥取大]
■【円のベクトル方程式】解き方のコツ
STEP 1:始点は1つに統一せよ
STEP 2:ベクトル方程式の基本形のいずれかに無理やり式変形せよ
└ベクトルの外分、内分の公式パターン
└円のベクトル方程式パターン
・基本形②:\(\small \mathrm{\overrightarrow{AP}\cdot\overrightarrow{BP}}=0\)(直径の円周角は90°に着目した関係式)を利用する
問題の式は既にすべて始点\(\small \mathrm{A}\)を基点とした形に整理されているので、基本形への式変形を考えればよい。今回着目しているのは点\(\small \mathrm{P}\)の位置なので、基点\(\small \mathrm{A}\)と着目点\(\small \mathrm{P}\)を結んだベクトルである\(\small \mathrm{\overrightarrow{AP}}\)に着目して整理していく。
\begin{equation}
\begin{split}
&\mathrm{\color{green}{\overrightarrow{AB}\cdot\overrightarrow{AC}}+\color{red}{\overrightarrow{AP}\cdot\overrightarrow{AP}}=\color{blue}{\overrightarrow{AB}\cdot\overrightarrow{AP}+\overrightarrow{AC}\cdot\overrightarrow{AP}}}\\
&\mathrm{\color{red}{\overrightarrow{AP}\cdot\overrightarrow{AP}}-\color{blue}{(\overrightarrow{AB}+\overrightarrow{AC})\cdot\overrightarrow{AP}}+\color{green}{\overrightarrow{AB}\cdot\overrightarrow{AC}}}=0\\
&\mathrm{(\overrightarrow{AP}-\overrightarrow{AB})\cdot(\overrightarrow{AP}-\overrightarrow{AC})}=0\\
&\mathrm{\overrightarrow{BP}\cdot\overrightarrow{CP}}=0 \quad \cdots ①\\
\end{split}
\end{equation}
(補足)ベクトルも因数分解みたいに変形しよう
途中2行目から3行目の式変形は因数分解の要領で式変形している。
少しわかりにくいと感じた人は、\(\small \mathrm{\overrightarrow{AP}}→x\)、\(\small \mathrm{\overrightarrow{AB}}→a\)、\(\small \mathrm{\overrightarrow{AC}}→b\)と置き換えてもらうと、\(\small \color{red}{x\cdot x-(a+b)x+ab=0}\)となり、
\begin{equation}
\begin{split}
x^2-(a+b)x+ab=0\\
(x-a)(x-b)=0
\end{split}
\end{equation}
となり、置き換えた文字をもとに戻してもらうと3行目の式と一致していることが分かるだろう。
【絶対覚えろ】ベクトル頻出の式変形
4行目から5行目の式変形は以下の公式を用いた。
ベクトルの問題ではほぼ必ず使う関係式なので、絶対に覚えること。
$$\color{red}{\mathrm{\overrightarrow{AB}=\overrightarrow{OB}-\overrightarrow{OA}}}$$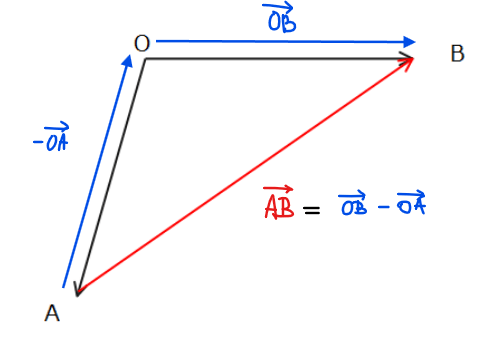
(補足)式変形の考え方
この式変形は、A→Bに直接行くのではなく、Oを経由していくことをあらわしている。
もう少し丁寧に式変形してあげるのであれば、
\begin{equation}
\begin{split}
\mathrm{\overrightarrow{AB}}&=\mathrm{\overrightarrow{A\color{red}O}+\overrightarrow{\color{red}OB} \qquad 点Oを経由}\\
\mathrm{\overrightarrow{AB}}&=\mathrm{\color{blue}{-\overrightarrow{OA}}+\overrightarrow{OB} \quad 向きを逆転}\\
\end{split}
\end{equation}
となり、先程の式を導くことができる。
①の式は、円のベクトル方程式の基本形②の形をしており、「点\(\small \mathrm{P}\)が線分\(\small \mathrm{BC}\)を直径とする円上」に存在することを表している。
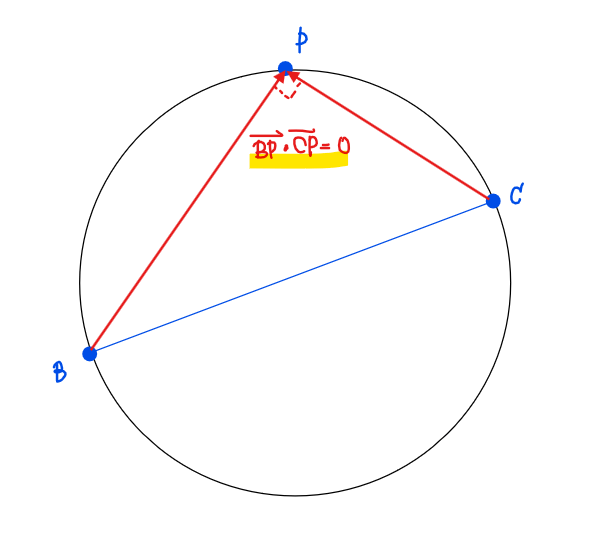
つまり\(\small \mathrm{\overrightarrow{BP}\cdot\overrightarrow{CP}}=0\) を満たすので、円を表す式になる
(解答)
線分\(\small \mathrm{BC}\)を直径とする円
【問題2】円のベクトル方程式の応用問題
座標平面上において、△\(\small \mathrm{ABC}\)は\(\small \mathrm{\overrightarrow{BA}\cdot\overrightarrow{CA}}=0\)を満たしている。この平面上の点\(\small \mathrm{P}\)が条件\(\small \mathrm{\overrightarrow{AP}\cdot\overrightarrow{BP}+\overrightarrow{BP}\cdot\overrightarrow{CP}+\overrightarrow{CP}\cdot\overrightarrow{AP}}=0\)を満たすとき、\(\small \mathrm{P}\)はどのような図形上の点であるか。 [類 岡山理科大]
■解き方の指針
・基本形①:\(\small |\mathrm{\overrightarrow{OP}- \overrightarrow{OC}} |=r \) (半径に着目した関係式)を利用する
・基本形①になるようにうまく平方完成する
問題文で与えられた条件式のベクトルの始点がバラバラになっているので、まずは始点を統一するところから。始点はどこでもOKなので、点\(\small \mathrm{A}\)を始点に選ぶことにする。
\begin{equation}
\begin{split}
&\mathrm{\overrightarrow{BA}\cdot\overrightarrow{CA}}=0\\
&\mathrm{(-\overrightarrow{AB})\cdot(-\overrightarrow{AC})}=0\\
&\mathrm{\overrightarrow{AB}\cdot\overrightarrow{AC}}=0 \quad \cdots ①\\
\end{split}
\end{equation}
(補足)ベクトルの基本性質
ベクトルの向きを逆にするときは「マイナス」符号をつければよい!
\begin{equation}
\begin{split}
&\mathrm{\overrightarrow{AP}\cdot\color{red}{\overrightarrow{BP}}+\color{red}{\overrightarrow{BP}}\cdot\color{blue}{\overrightarrow{CP}}+\color{blue}{\overrightarrow{CP}}\cdot\overrightarrow{AP}}=0\\
&\mathrm{\overrightarrow{AP}\cdot\color{red}{(\overrightarrow{AP}-\overrightarrow{AB})}+\color{red}{(\overrightarrow{AP}-\overrightarrow{AB})}\cdot\color{blue}{(\overrightarrow{AP}-\overrightarrow{AC})}+\color{blue}{(\overrightarrow{AP}-\overrightarrow{AC})}\cdot\overrightarrow{AP}}=0\\
\end{split}
\end{equation}
ここで、1行目から2行目の式変形は問題1でも紹介したベクトル頻出の式変形を利用した。あとは頑張って展開して整理すると、
\begin{equation}
\begin{split}
&\mathrm{|\overrightarrow{AP}|^2-\overrightarrow{AP}\cdot\overrightarrow{AB}}\\
&\mathrm{\quad +|\overrightarrow{AP}|^2-\overrightarrow{AP}\cdot\overrightarrow{AB}-\overrightarrow{AP}\cdot\overrightarrow{AC}+\color{magenta}{\overrightarrow{AB}\cdot\overrightarrow{AC}}}\\
&\mathrm{\qquad+|\overrightarrow{AP}|^2-\overrightarrow{AP}\cdot\overrightarrow{AC}}=0\\
&\mathrm{3|\overrightarrow{AP}|^2-2\overrightarrow{AP}\cdot\overrightarrow{AB}-2\overrightarrow{AP}\cdot\overrightarrow{AC}}=0
\end{split}
\end{equation}
ただし、途中の紫色箇所は式①の条件から0になる。
ここから基本形に無理やり変形していくのだが、なかなか大変…。\(\small \mathrm{|\overrightarrow{AP}|^2}\)と2乗の形があることから、円のベクトル方程式の基本形になるように式変形を進めていく。ベクトルだと分かりにくいが、式の形から、「\(\small 3x^2-2xy-\cdots\)」のような形をしていることから、「(括弧)\(\small ^2\)」の形に平方完成する方針で考える。
\begin{equation}
\begin{split}
&\mathrm{3|\overrightarrow{AP}|^2-2\overrightarrow{AP}\cdot\color{red}{(\overrightarrow{AB}+\overrightarrow{AC})}}=0
\end{split}
\end{equation}
赤字の部分がごちゃごちゃしているのでひとまとまりの文字として置き換える。そのまま置き換えてもよいのだが、図形的な意味を意識して置き換えるのであれば、
\begin{equation}
\begin{split}
&\mathrm{3|\overrightarrow{AP}|^2- 2 \color{blue}{\times2}\times \overrightarrow{AP}\cdot\color{red}{\frac{\overrightarrow{AB}+\overrightarrow{AC}}{\color{blue}2}}}=0\quad \cdots②
\end{split}
\end{equation}
と2を割り込ませておき
\begin{equation}
\begin{split}
&\mathrm{\overrightarrow{AM}=\frac{\overrightarrow{AB}+\overrightarrow{AC}}{2}}\quad \cdots③
\end{split}
\end{equation}
とおくと、ベクトルの内分の公式から点\(\small \mathrm{M}\)は線分BCの中点になるので、あとでどのような図形かを説明する際に役立つ。
では、③を②に代入して平方完成をすると
\begin{equation}
\begin{split}
&\mathrm{3|\overrightarrow{AP}|^2-4\overrightarrow{AP}\cdot\overrightarrow{AM}}=0\\
&\mathrm{|\overrightarrow{AP}|^2-\dfrac{4}{3}\overrightarrow{AP}\cdot\overrightarrow{AM}}=0\\
&\mathrm{|\overrightarrow{AP}|^2-\dfrac{4}{3}\overrightarrow{AP}\cdot\overrightarrow{AM}\color{magenta}{+\frac{4}{9}|\overrightarrow{AM}|^2}=\color{magenta}{\frac{4}{9}|\overrightarrow{AM}|^2}}\\
&\mathrm{\color{red}{\left|\overrightarrow{AP}-\dfrac{2}{3}\overrightarrow{AM}\right|^2}=\frac{4}{9}|\overrightarrow{AM}|^2}\\
&\mathrm{\left|\overrightarrow{AP}-\dfrac{2}{3}\overrightarrow{AM}\right|=\frac{2}{3}|\overrightarrow{AM}|}\quad \cdots④\\
\end{split}
\end{equation}
最後の式は、円のベクトル方程式の基本形①なので、式の定義と見比べると、\(\small \mathrm{\dfrac{2}{3}\overrightarrow{AM}}\)が円の中心で、\(\small \mathrm{\dfrac{2}{3}|\overrightarrow{AM}|}\)が円の半径(今回はたまたまどちらも同じ)と分かる。
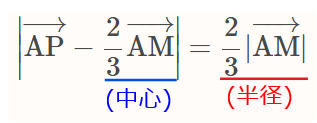
最後に点\(\small \mathrm{P}\)がどのような図形上にあるかを言葉で説明すればよい。いきなり数式を言語化するのは難しいので、まずは一旦図を描いてみるのがおすすめ。
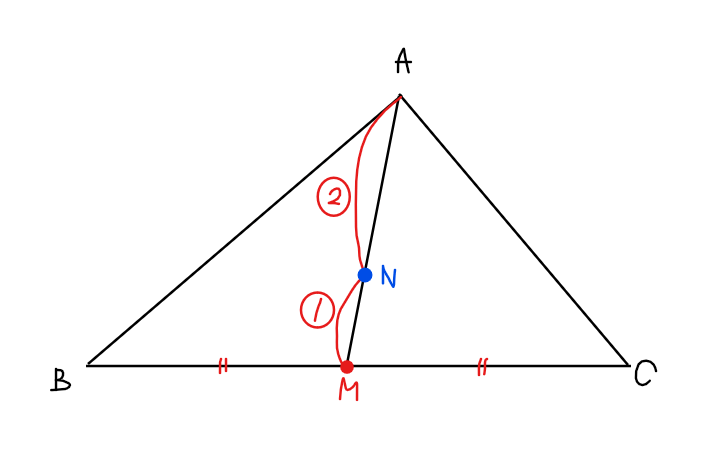
点Mは②から線分BCの中点。\(\small \mathrm{\dfrac{2}{3}\overrightarrow{AM}}\)については、点Aから点Mへ向かうベクトル\(\small \mathrm{\overrightarrow{AM}}\)の\(\small \mathrm{\dfrac{2}{3}}\)倍という意味なので、線分AMを2:1に内分する点になる。上図ではこの点を新たに点Nとおいた。
\begin{split}
&\mathrm{\overrightarrow{AN}=\dfrac{2}{3}\overrightarrow{AM}}\\
&\mathrm{|\overrightarrow{AN}|=\dfrac{2}{3}|\overrightarrow{AM}|}\\
\end{split}
この式を④に代入してあげると、
\begin{split}
&\mathrm{|\overrightarrow{AP}-\overrightarrow{AN}|=|\overrightarrow{AN}|}\\\
\end{split}
となるので、中心が\(\small \mathrm{\overrightarrow{AN}}\)、半径が\(\small \mathrm{|\overrightarrow{AN}|}\)の円、つまり、点Nを中心とした半径ANの円となる。
あとは、このままだと点Nが自分で設定した点になっているので、仕上げにその説明を加えてあげればよいだろう(解答をかくときには自分で設定した点が含まれていないかに注意しましょう)。
(解答)
線分BCの中点をMとし、線分AMを2:1に内分する点をNとすると、点Pは点Nを中心とした半径ANの円上の点である。
本記事のまとめ
今回は円のベクトル方程式を使った問題の解き方について解説しました。
■【円のベクトル方程式】解き方のコツ
STEP 1:始点は1つに統一せよ
STEP 2:ベクトル方程式の基本形のいずれかに無理やり式変形せよ
└ベクトルの外分、内分の公式パターン
└円のベクトル方程式パターン
ちなみに、今回は扱いませんでしたが、始点と求める点を結ぶベクトルが単純な1次式であれば、内分、外分の公式パターンに式変形できます。今回の\(\small \mathrm{|\overrightarrow{AP}|^2}\)のように2次式になっている場合は円のベクトル方程式の基本形に変形してあげましょう。
■円のベクトル方程式の基本形2パターン
・基本形①:\(\small |\mathrm{\overrightarrow{OP}- \overrightarrow{OC}} |=r \) …半径に着目した関係式
・基本形②:\(\small \mathrm{\overrightarrow{AP}\cdot\overrightarrow{BP}}=0\) …直径の円周角は90°に着目した関係式

特に、基本形①に変形するときには途中で平方完成の要領で2乗の形を作ってあげるのがコツです。初見だと式変形の仕方に戸惑うと思うので、「\(\small \mathrm{|\overrightarrow{AP}|^2}\)が出てきたら平方完成」としっかり覚えておきましょう。
他にもベクトルの問題が解きたい人は下にある関連記事もチェックしてみてください!
では、今回はここまでです。お疲れさまでした!






コメント