【苦手な人必見】空間図形のベクトル問題を解説（共線・共面条件の利用、垂線ベクトルの求め方）

今回は、空間図形のベクトル問題の中でも苦手な人が多い「共線・共面条件を使って問題を解く」と「垂線のベクトルを求める問題」をメインにわかりやすく解説していこうと思います。前半は問題を解く上での前提知識や考え方、後半は実際の入試問題を例に演習・解説する構成になっていますので、ぜひ最後までチェックしてみてください！

　こんな人におすすめ

共線共線面条件を問題の中でどう使えばいいのかわからない
垂線の足のベクトル表示や座標など延長線と平面の交点のベクトルの求め方が分からない
空間図形のベクトルの解き方のコツが知りたい

　本記事のレベル

重要度

低

1

2

3

4

5

高
難易度

易しい

1

2

3

4

5

難しい
暗記/理解

暗記重視

1

2

3

4

5

理解重視

1.【知識編】ベクトル問題でよく使う公式集
2.【解法編】解き方のコツ
1. 2.1 覚えておくべきキーワード2選
2. 2.2 ベクトルにこだわるな
3.【演習編】苦手な人が多い問題を解こう
1. 3.1【問題1】共線・共面条件の利用
2. 3.2【問題2】垂線ベクトルの求め方
4.まとめ

1.【知識編】ベクトル問題でよく使う公式集

まずは、問題を解く上でよく使う公式や考え方を4つ厳選して紹介します。

1.1 共線条件・共面条件

共線条件とは、2つの点が同じ線上に存在するための条件をベクトルで表したものです。

■共線条件
点Aと点Bが同一直線上にあるための条件は、実数$\small t$を用いて $$\overrightarrow{OB}=t\overrightarrow{OA}$$ で表される。

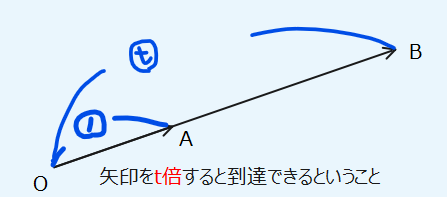
この公式は、同じ線上の点ということは、ベクトルの矢印を伸ばしたり縮めたりすることでその点を指差しできるということを表してます。

共面条件とは、3つのベクトルで作られる平面上に点が存在する条件を表したものです。

■共面条件
3つのベクトル$\small \overrightarrow{OA}$、$\small \overrightarrow{OB}$、$\small \overrightarrow{OC}$で作られる面上の点Pを3つのベクトルの和で$\small \overrightarrow{OP}=\ell\overrightarrow{OA}+m\overrightarrow{OB}+n\overrightarrow{OC}$と表した場合、ベクトルの係数について $$\ell+m+n=1$$ が成り立つ。

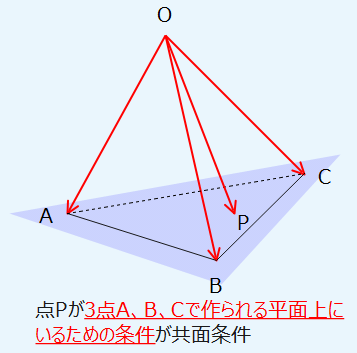
「3つのベクトルの係数の和が1になる」と覚えておくとよいでしょう。

実際の問題では、ある点を延長させた線と面の交点のベクトルや座標を求める問題が頻出で、共線条件の後に共面条件を使うことが多いのでセットで覚えておきましょう。

1.2 内分/外分点の公式、内積の公式

証明は省きますが、空間図形のベクトル問題では必須の知識なので覚えておきましょう。図形の公式を覚えるときには、式だけを覚えるのではなく図とセットで覚えると問題が解きやすくなるので図もセットで載せておきます！

■内分/外分点の公式

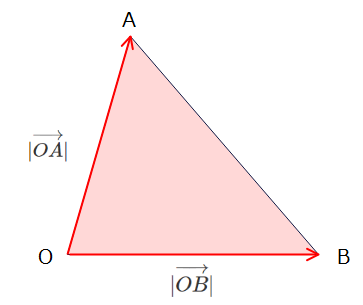
・三角形OABの辺ABをm:nに内分する点Pは
$$\overrightarrow{OP}=\frac{n\overrightarrow{OA}+m\overrightarrow{OB}}{m+n}$$

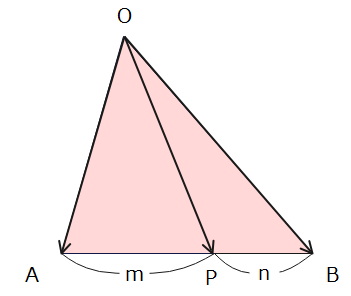
・三角形OABの辺ABをm:nに外分する点Pは
$$\overrightarrow{OP}=\frac{-n\overrightarrow{OA}+m\overrightarrow{OB}}{m-n}$$

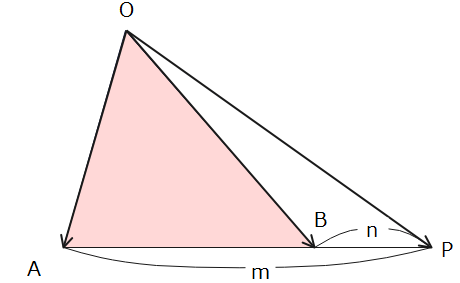
■内積の公式

$$\overrightarrow{OA}\cdot\overrightarrow{OB}=|\overrightarrow{OA}||\overrightarrow{OB}|\cos \angle AOB$$

1.3 余弦定理

ベクトルの問題は大きくは図形問題に分類されるため、余弦定理やメネラウスの定理などの図形問題の公式がよく出てきます。これはベクトルの知識ではないのですが、問題の中でよく出るという意味で、ここではその中で最も使われる公式である余弦定理を載せておきます。

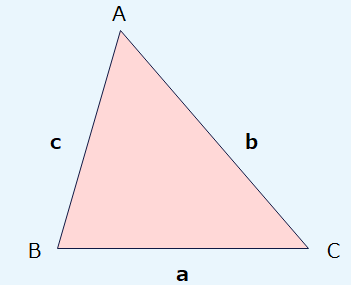
■余弦定理

$$a^2 = b^2 + c^2 -2bc\cos A$$

1.4 最大値・最小値の計算（2次関数、相加・相乗平均など）

最後はこちらもベクトルの知識ではないので、知っている人は読み飛ばしてokです。ベクトルの問題では、小問の最後にベクトルの長さや面積の最大値や最小値を求める問題がよく出てきます。基本的には、2次関数で解くことができますが、相加相乗平均を使うことで楽に計算できることがあるので、ここでは相加相乗平均の公式を紹介します。

正の数$\small a$、$\small b$に対して $$a+b≧2\sqrt{ab}$$ が成り立つ。等号成立は、$\small a=b$のとき。

2.【解法編】解き方のコツ

2.1 覚えておくべきキーワード2選

基本的な解き方は平面図形のベクトル問題と同じく、問題文のキーワードに対して公式を使って解いていくキーワード反応になります。例えば、「２つのベクトルが垂直＝内積が0で立式」などです。キーワードについては、平面図形と重なる部分も多いので詳細は「平面図形のベクトル問題の解法（ベクトル計算の基礎と内積の活用）」を見ていただければと思いますが、空間図形では、新たに空間図形特有のキーワードが2つあるのでそれを紹介します。これはとても重要なポイントなので絶対に覚えましょう！

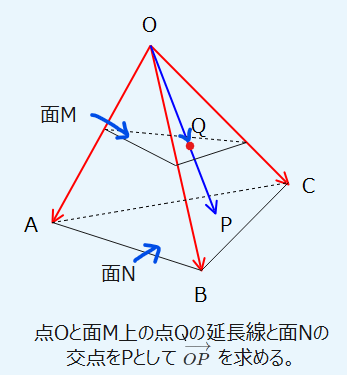
3点A、B、Cでできる平面と直線（延長線）の交点を求める。

→共線条件でベクトル$\small \overrightarrow{OP}$を表した後に、共面条件（3点のベクトル$\small \overrightarrow{OA},\overrightarrow{OB},\overrightarrow{OC}$の係数の和=1）を利用。
垂線の長さ・垂線の足の位置ベクトルを求める。

→共面条件（ベクトルの係数を$\small \ell,m,n$などとおいて）を利用して、内積=0で解く。

2.2 ベクトルにこだわるな

もう一点ポイントとして意識しておきたいのが、「必ずしもベクトルを使って解かなくてもよい」という考え方です。ベクトルの問題なのにベクトルを使わないの！？と驚いた人もいるかもしれませんが、その通りです。

「ベクトルの問題だから絶対にベクトルを使って解くはずだ」と思い込んでしまい、解き方の選択肢が狭まってしまい解けてないという人も意外と少なくありません。個人的な感覚だと、ベクトルの問題は3つ程度の小問に分かれることが多いですが、後半の小問はベクトルを使わずに、図形知識で解いたり、2次関数の最小値・最大値の問題に派生していることも珍しくないので、少し考えてベクトルで解けなさそうだなと思ったら、ベクトル以外の方法で解けないかを考えてみるのもよいかと思います。

3.【演習編】苦手な人が多い問題を解こう

3.1【問題1】共線・共面条件の利用

問題[大阪電通大]

四面体OABCにおいて、$\small \vec{a}=\overrightarrow{OA}$、$\small \vec{b}=\overrightarrow{OB}$、$\small \vec{c}=\overrightarrow{OC}$とおく。
(1)線分ABを1:2に内分する点をPとし、線分PCを2:3に内分する点をQとする。$\small \overrightarrow{OQ}$を$\small \vec{a},\vec{b},\vec{c}$を用いて表せ。
(2)D、E、Fはそれぞれ線分OA、OB、OC上の点で、$\small OD=\frac{1}{2}OA$、$\small OE=\frac{2}{3}OB$、$\small OF=\frac{1}{3}OC$とする。3点、D、E、Fを含む平面と線分OQの交点をRとするとき、$\small \overrightarrow{OR}$を$\small \vec{a},\vec{b},\vec{c}$を用いて表せ。

解説

(1)問題文を図式化すると以下の通り。

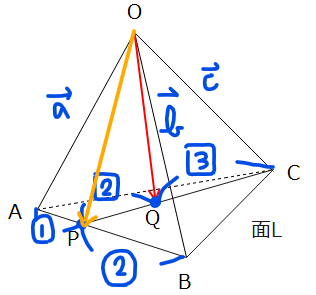
求めるベクトル$\small \overrightarrow{OQ}$は赤色の矢印です。これを求めるには、△OPCに着目して内分点の公式を使ってあげます。

$$\overrightarrow{OQ}=\frac{3\cdot\overrightarrow{OP}+2\cdot\vec{c}}{2+3}=\frac{3}{5}\overrightarrow{OP}+\frac{2}{5}\vec{c}\quad \cdots①$$

オレンジのベクトル$\small \overrightarrow{OP}$は、今度は△OABに着目して内分点の公式を使うことで、

$$\overrightarrow{OP}=\frac{2\cdot\vec{a}+1\cdot\vec{b}}{1+2}=\frac{2}{3}\vec{a}+\frac{1}{3}\vec{b}\quad\cdots②$$

②を①に代入することで、

$$
\begin{equation}
\begin{split}
\overrightarrow{OQ} & =\frac{3}{5}\left(\frac{2}{3}\vec{a}+\frac{1}{3}\vec{b}\right)+\frac{2}{5}\vec{c}\\
&=\frac{2}{5}\vec{a}+\frac{1}{5}\vec{b}+\frac{2}{5}\vec{c}\cdots(答)
\end{split}
\end{equation}
$$

(2)問題文の状況を図示すると以下の通り。

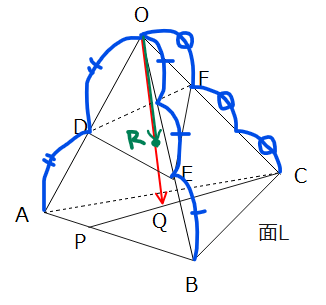
$\small OE=\frac{2}{3}OB$ということは、辺OBを3等分したうちの2つ分が線分OEということなので、図の位置に点Eがあることになります。他の点も同様。

図を描くとわかるように、「点Rと点Qが同一直線上にある」はキーワード1つ目の形なので、共線条件→共面条件の順で解いていきます。

まず、$\small \overrightarrow{OQ}$と$\small \overrightarrow{OR}$は同一直線上にあるので、共線条件から$\small \overrightarrow{OR}=t\overrightarrow{OQ}$とおけるので、

$$\overrightarrow{OR} =\frac{2}{5}t\vec{a}+\frac{1}{5}t\vec{b}+\frac{2}{5}t\vec{c}\cdots③$$

次に、四面体ODEFに着目すると、共面条件から、

$$
\begin{equation}
\begin{split}
\overrightarrow{OR}　&=\ell\overrightarrow{OD}+m\overrightarrow{OE}+n\overrightarrow{OF}\\
&=\frac{1}{2}\ell\vec{a}+\frac{2}{3}m\vec{b}+\frac{1}{3}n\vec{c}\cdots④
\end{split}
\end{equation}
$$

ただし、$\small \ell+m+n=1$。

③と④はどちらも同じ$\small \overrightarrow{OR}$を表しているので、係数比較から、

$$
\begin{equation}
\begin{split}
&\frac{1}{2}\ell=\frac{2}{5}t\\
&\frac{2}{3}m=\frac{1}{5}t\\
&\frac{1}{3}n=\frac{2}{5}t
\end{split}
\end{equation}
$$

これらを解いて

$$
\begin{equation}
\begin{split}
&\ell=\frac{4}{5}t\\
&m=\frac{3}{10}t\\
&n=\frac{6}{5}t
\end{split}
\end{equation}
$$

$\small \ell+m+n=1$（共面条件）より、

$$
\ell+m+n=\frac{4}{5}t+\frac{3}{10}t+\frac{6}{5}t=\frac{23}{10}t=1
$$

よって、$\small t=\frac{10}{23}$。

この結果を③に代入することで、

$$
\begin{equation}
\begin{split}
\overrightarrow{OR} &=\frac{2}{5}\times\frac{10}{23}\vec{a}+\frac{1}{5}\times\frac{10}{23}\vec{b}+\frac{2}{5}\times\frac{10}{23}\vec{c}\\
&=\frac{4}{23}\vec{a}+\frac{2}{23}\vec{b}+\frac{4}{23}\vec{c}\cdots(答)
\end{split}
\end{equation}
$$

3.2【問題2】垂線ベクトルの求め方

問題[類関西学院大]

座標空間の原点Oから、3点 A(1,0,1)、B(2,-1,0)、C(1,1,2)を通る平面に垂線をOHを下すとき、点Hの座標と線分OHの長さを求めよ。

解説

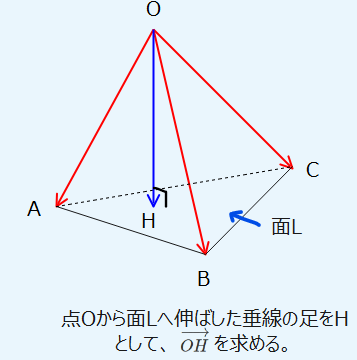
まずは問題を図式化します。ちなみに、座標の位置関係はざっくりでokです（ベクトル計算するのであまり細かい位置は関係ない）。

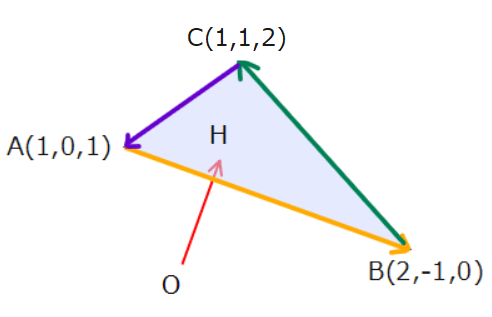
今回は「平面に対して垂線を下す」というキーワードがあるので、「共面条件を利用して内積＝０」の流れで解いてきましょう。

共面条件から、

$$\overrightarrow{OH}=\ell \overrightarrow{OA}+m\overrightarrow{OB}+n\overrightarrow{OC}\quad \cdots (★)$$

ただし、$\small \ell +m+n=1$。

今回みたいに四面体ではない場合でも共面条件は使えるのでしょうか？

使えます！そもそも空間図形のベクトル問題で四面体が多く出てくるのは、1点と平面を考えることが多いからです。どういうことかというと今回の問題も原点Oと3点A、B、Cの平面を考えていて、これらの点を線で結ぶと下図のような四面体が出来上がります。

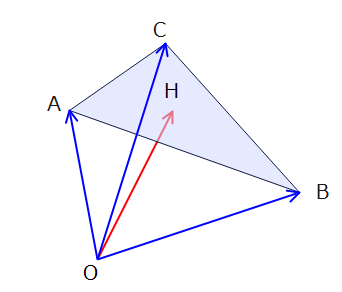
これは、合計で4点が登場しているため四面体になるということで高校数学では頻出なので空間ベクトルが出てきたら四面体を作ってあげると考えやすいかもしれません。

ここで、$\small \overrightarrow{OA}$、$\small \overrightarrow{OB}$、$\small \overrightarrow{OC}$それぞれ成分表示は、点A、B、Cの座標になるので、$\small \overrightarrow{OH}$を成分表示すると、

$$
\begin{equation}
\begin{split}
\overrightarrow{OH} &=\ell
\begin{pmatrix}
1\\ 0\\ 1
\end{pmatrix}
+m
\begin{pmatrix}
2\\ -1\\ 0
\end{pmatrix}
+n
\begin{pmatrix}
1\\ 1\\ 2
\end{pmatrix}\\
&=\begin{pmatrix}
\ell +2m +n\\ -m+n\\ \ell +2n
\end{pmatrix}
\quad \cdots ①
\end{split}
\end{equation}
$$

ちなみに、括弧の向きは高校数学では横書きだと思いますが、数学界ではベクトル成分は縦書きがスタンダードなので、本記事では縦書きします（見やすいし）。もちろん横書きでもokです。上から順に$\small x,y,z$座標の成分です。

次に、平面ABC上のベクトルは$\small \overrightarrow{OH}$とどれも垂直になるので、初めの図のそれぞれのベクトル（オレンジ、緑、紫）との内積は0になります。

それぞれのベクトルの成分は、

$$
\begin{equation}
\begin{split}
\overrightarrow{AB}&=\overrightarrow{OB}-\overrightarrow{OA}\\
&=
\begin{pmatrix}
2\\ -1\\ 0
\end{pmatrix}
–
\begin{pmatrix}
1\\ 0\\ 1
\end{pmatrix}\\
&=
\begin{pmatrix}
1\\ -1\\ -1
\end{pmatrix}\quad \cdots ②
\end{split}
\end{equation}
$$

他も同様に計算すると

$$
\overrightarrow{BC}=
\begin{pmatrix}
-1\\ 2\\ 2
\end{pmatrix}\quad \cdots ③
$$

$$
\overrightarrow{CA}=
\begin{pmatrix}
0\\ -1\\ -1
\end{pmatrix}\quad \cdots ④
$$

ちなみに、今回はこの3つのベクトルにしましたが、他にも$\small \overrightarrow{AC}$みたいに向きが逆のベクトルでも大丈夫です。

では、最後にそれぞれベクトルと$\small \overrightarrow{OH}$との内積を計算していきます。ベクトル成分は3つ求めましたが、そのうちの2つとの内積しか使わないので、②と④を使うことにします。どれを選んでも結果は同じなので、計算のしやすさで選びましょう。④は$\small x$成分が0なので内積計算がしやすいですね。

①と②の内積より

$$
\begin{equation}
\begin{split}
\overrightarrow{OH} \cdot \overrightarrow{AB}&=
\begin{pmatrix}
\ell +2m +n\\ -m+n\\ \ell +2n
\end{pmatrix}\cdot
\begin{pmatrix}
1\\ -1\\ -1
\end{pmatrix}\\
&=(\ell +2m +n)-(-m+n)-(\ell +2n)\\
&=3m-2n=0\\
&m=\frac{2}{3}n \quad \cdots ⑤\\
\end{split}
\end{equation}
$$

①と④の内積は

$$
\begin{equation}
\begin{split}
\overrightarrow{OH} \cdot \overrightarrow{CA}&=
\begin{pmatrix}
\ell +2m +n\\ -m+n\\ \ell +2n
\end{pmatrix}\cdot
\begin{pmatrix}
0\\ -1\\ -1
\end{pmatrix}\\
&=-(-m+n)-(\ell +2n)\\
&=-\ell +m-3n=0\\
\end{split}
\end{equation}
$$

ここで⑤の結果より、

$$
\begin{equation}
\begin{split}
&-\ell +\frac{2}{3}n-3n=0\\
&-\ell -\frac{7}{3}n=0\\
&\ell=-\frac{7}{3}n \quad \cdots ⑥
\end{split}
\end{equation}
$$

⑤、⑥の結果と共面条件$\small \ell +m+n=1$より

$$
\begin{equation}
\begin{split}
&-\frac{7}{3}n +\frac{2}{3}n +n=1\\
&-7n+2n+3n=3\\
&-2n=3\\
&n=-\frac{3}{2}\\
\end{split}
\end{equation}
$$

⑤、⑥より、$\small m=-1,\ell=\frac{7}{2}$。

よって、(★)より、

$$
\begin{equation}
\begin{split}
\overrightarrow{OH}&=\frac{7}{2} \overrightarrow{OA}-\overrightarrow{OB}-\frac{3}{2}\overrightarrow{OC}\\
&=\frac{7}{2}
\begin{pmatrix}
1\\ 0\\ 1
\end{pmatrix}
–
\begin{pmatrix}
2\\ -1\\ 0
\end{pmatrix}
-\frac{3}{2}
\begin{pmatrix}
1\\ 1\\ 2
\end{pmatrix}\\
&=
\begin{pmatrix}
0\\ -\frac{1}{2}\\ \frac{1}{2}
\end{pmatrix}
\end{split}
\end{equation}
$$

よって、$\small \mathrm{H}(0,-\frac{1}{2},\frac{1}{2})$…（答）。

OHの長さは、

$$
\begin{equation}
\begin{split}
|\overrightarrow{OH}| &=\sqrt{\left(-\frac{1}{2}\right)^2+\left(\frac{1}{2}\right)^2}\\
&=\sqrt{\frac{1}{2}}\\
&=\frac{\sqrt{2}}{2}\quad\cdots(答)
\end{split}
\end{equation}
$$