平面図形のベクトル問題の解法（ベクトル計算の基礎と内積の活用）

こんにちは。当サイト管理人のhiroemonです。

本記事では、平面図形のベクトル問題を解くときに必ず必要になる「ベクトル計算の基礎」や「内積」を使う問題の解き方を解説していきたいと思います。「内積の計算はできるけど問題の中でどう使うの？」、「基点をもとにベクトルを分解する方法が分からない…」、「ベクトル問題を解くコツが知りたい！」という方必見の解説記事になっていますので、ぜひ最後まで確認してみてください！

　分野のレベル

重要度

低

1

2

3

4

5

高
難易度

易しい

1

2

3

4

5

難しい
暗記/理解

暗記重視

1

2

3

4

5

理解重視

1.【解説編】ベクトル問題の基本的な解き方/基礎知識
2.【問題編】ベクトルの図形問題
1. 2.1【問題1】平面図形上のベクトル計算
2. 2.2【問題2】ベクトルの成分計算の利用
3.まとめ

1.【解説編】ベクトル問題の基本的な解き方/基礎知識

ベクトルの問題には様々な種類がありますが、平面図形の問題で一番基本的な考え方をはじめに紹介します。基本的には以下の3点を意識して解いていくことになります。

POINT 1：問題文を図示する。
POINT 2：基点をベースにベクトルを分解。
POINT 3：キーワードから条件式を立てる。

1.1【POINT1】問題文を図示する

平面図形と絡めたベクトルの問題は、ベクトル計算ももちろん大事なのですが、図形問題だけあって、数式を見て計算しているだけでは解けません。問題文だけを読んで、状況がイメージできる人はほとんどいないでしょう。やっぱり、視覚から得られる情報やイメージのしやすさは圧倒的なので、面倒がらずにちゃんと書くようにしましょう。個人的な見解として、ベクトルが苦手な人の多くは、図を描いてなかったり、描いていてもメモ書きレベルでとても小さくごにょごにょしている人が多いです。

図をしっかり描くだけで解きやすさが格段に上がるので、書かない手はないですね！

1.2【POINT2】基点をベースにベクトルを分解

まず初めに簡単に用語のおさらいです。

・始点：ベクトルのスタート地点
・終点：ベクトルのゴール地点
・基点：基準となる始点（＝全部のベクトルのスタート地点）

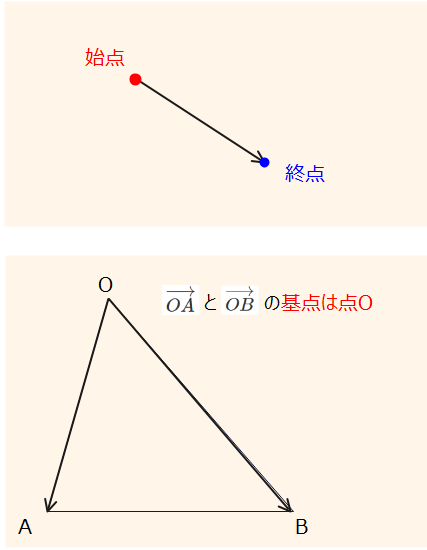
図形が関係するベクトル問題の大半は基点が指定されていることが多いです。指定されていない場合は、自分で設定しましょう。そして、平面図形であれば、2次元なので2つのベクトルの和で表すことができますが、この2つのベクトルの始点がバラバラだと、うまく計算ができないので、すべてのベクトルの基点を必ず1つに統一しましょう。

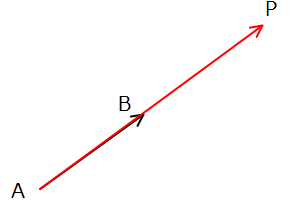
★具体例

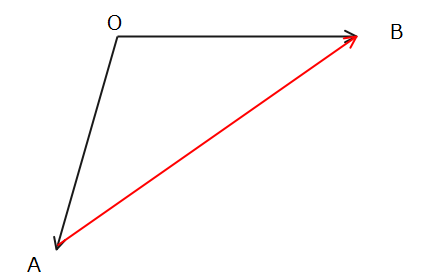
例えば、上の図で$\small \overrightarrow{AB}$がある場合は、$\small \overrightarrow{AB}=\overrightarrow{OB}-\overrightarrow{OA}$のように基点Oからの2つのベクトルに分解して計算を進めるのがよいでしょう。

$$\overrightarrow{AB}=\overrightarrow{OB}-\overrightarrow{OA}$$ この式は、問題を解く上でよく使う公式なので必ず覚えておきましょう。A→Bへのベクトルは、後（B）-先（A）になります。
ちなみに、暗記が嫌いな私は忘れた時は以下のように導き出しています。
$$\overrightarrow{AB}=\overrightarrow{AO}+\overrightarrow{OB}=\overrightarrow{OB}-\overrightarrow{OA}$$ ※始点と終点をひっくり返す（矢印の向きを逆にする）と符号がマイナスになるので、$\small \overrightarrow{AO}=-\overrightarrow{OA}$。

1.3【POINT3】キーワードから条件式を立てる

ベクトル問題では、問題文にいくつかお決まりのキーワードが存在します。つまり、「この言葉が出てきたら、この公式を使って計算すればいい」というパターンがあるのでそれをリスト化しました。これらはしっかり覚えておきましょう。

$\small \vec{a}$と$\small \vec{b}$が垂直になる（直交する）。
→$\small \vec{a} \cdot \vec{b}=0$(ベクトルの内積が0)
$\small \overrightarrow{AB}$の延長線上に点Pを取る。
→$\small \overrightarrow{AP}=t\overrightarrow{AB}$ ($\small t$は実数)

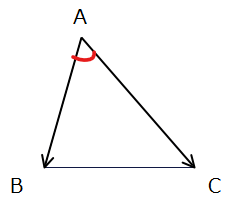
$\small \overrightarrow{AB}$と$\small\overrightarrow{AC}$の内積を求めよ。
→△ABCで余弦定理などを用いて$\small \cos A$(ベクトルに挟まれた角度)を求める。

2.【問題編】ベクトルの図形問題

ここからは前章の解き方を具体的な問題を通して確認していきましょう。

2.1【問題1】平面図形上のベクトル計算

問題[千葉大　類題]

3辺の長さがOA=2、OB=3、AB=$\small \sqrt{7}$の三角形OABがある。辺OAの中点をMとし、Bを始点とする半直線BM上にBP=$\small t$BMとなる点Pをとり、$\small \overrightarrow{OA}=\vec{a}$、$\small \overrightarrow{OB}=\vec{b}$とする。
(1)$\small \overrightarrow{OP}$を$\small \vec{a}$、$\small \vec{b}$と$\small t$を用いて表せ。
(2)$\small \vec{a}$と$\small \vec{b}$の内積を求めよ。
(3)$\small \overrightarrow{AP} \perp \overrightarrow{BM}$となるとき、$\small t$の値を求めよ。

解答

(1)$\small \overrightarrow{OP}=\frac{t}{2}\vec{a}-(t-1)\vec{b}$
(2)$\small \vec{a} \cdot \vec{b}=3$
(3)$\small t =\frac{13}{14}$

解説(1)

解説編のPOINT1でも述べた通り、平面図形の問題は、まずは図形を描きましょう。

図示するうえで、少し表現が難しい「Bを始点とする半直線BM上にBP=$\small t$BMとなる点Pをとり」の部分を補足しておきます。「半直線」とは「スタート地点はあるけどゴール地点がない線」のことです。直線がスタートもゴールもない無限に伸びた線のことなので、スタートがあるから半分直線という意味ですね。つまり、補足部分の意味は、「点BをスタートとしてMを通るように伸ばした線上にBMを$\small t$倍した点Pを取るよ」ということです。

これを踏まえて問題文の内容を図示すると以下のようになります。

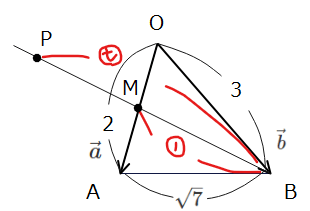
図示できたら、次はPOINT2の基点をベースにベクトルを分解していきます。この問題では「BP=$\small t$BM」とあるので、これはそのままベクトルの関係式として$\small \overrightarrow{BP}=t \overrightarrow{BM}$と表すことができます。この関係式を基点Oをベースに分解していくと、

$$
\begin{equation}
\begin{split}
&\overrightarrow{BP}=t \overrightarrow{BM}\\
&\overrightarrow{OP}-\overrightarrow{OB}=t( \overrightarrow{OM}-\overrightarrow{OB} )\\
\end{split}
\end{equation}
$$

ここで、点MはOAの中点なので、$\small \overrightarrow{OM}=\frac{1}{2}\vec{a}$、$\small \overrightarrow{OB}=\vec{b}$なので、

$$
\begin{equation}
\begin{split}
&\overrightarrow{OP}-\overrightarrow{OB}=t( \overrightarrow{OM}-\overrightarrow{OB} )\\
&\overrightarrow{OP}-\vec{b}=t\left(\frac{1}{2}\vec{a}-\vec{b}\right)\\
&\overrightarrow{OP}-\vec{b}=\frac{t}{2}\vec{a}-t\vec{b}\\
&\overrightarrow{OP}=\frac{t}{2}\vec{a}-t\vec{b}+\vec{b}\\
&\overrightarrow{OP}=\frac{t}{2}\vec{a}-(t-1)\vec{b} \quad \cdots (答)
\end{split}
\end{equation}
$$

解説(2)

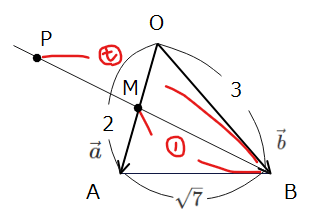
これは、問題文に「内積」のキーワードがあるので、POINT3のキーワードから条件を立てる方法で解いていきます。$\small \vec{a}$と$\small \vec{b}$の内積なので、$\small \cos \angle AOB$を求めていきましょう。

△OABに対して余弦定理から、

$$
\begin{equation}
\begin{split}
&AB^2 =OA^2+OB^2-2OA \cdot OB \cos \angle AOB\\
& 7= 4+9-12\cos \angle AOB\\
& -6=-12\cos \angle AOB\\
& \cos \angle AOB = \frac{1}{2}\\
\end{split}
\end{equation}
$$

よって、$\small \vec{a} \cdot \vec{b}=|a|\cdot|b|\cos \angle AOB$なので、$\small \vec{a} \cdot \vec{b}=2\times3\times\frac{1}{2}=3 \cdots $(答)。

解説(3)

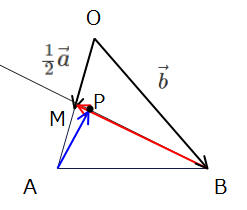
$\small \overrightarrow{AP}$と$\small \overrightarrow{BM}$が垂直だという条件から、$\small \overrightarrow{AP}\cdot \overrightarrow{BM}=0$を計算していきましょう。ちなみに、$\small t$はBMを何倍したらBPかという値なので、上図を見る限りだと1より少し小さい値になりそうだという予想がつきます。これはあくまで図が正しくかけていたらの話なので、最後検算の時の参考として確認できればokです。

さて、内積計算の前に$\small \overrightarrow{AP},\overrightarrow{BM}$は基点Oがベースになっていないので、POINT2に従って分解します。

$$
\begin{equation}
\begin{split}
\overrightarrow{AP}&=\overrightarrow{OP}-\overrightarrow{OA}\\
& = \left(\frac{t}{2}\vec{a}-(t-1)\vec{b} \right) -\vec{a}\\
& = \left(\frac{t}{2}-1\right)\vec{a}-(t-1)\vec{b} \quad \cdots ①
\end{split}
\end{equation}
$$

$$
\begin{equation}
\begin{split}
\overrightarrow{BM}&=\overrightarrow{OM}-\overrightarrow{OB}\\
& = \frac{1}{2}\vec{a}-\vec{b} \quad \cdots ②
\end{split}
\end{equation}
$$

①、②を$\small \overrightarrow{AP}\cdot \overrightarrow{BM}=0$に代入すると、

$$
\begin{equation}
\begin{split}
&\left( \left(\frac{t}{2}-1\right)\vec{a}-(t-1)\vec{b} \right)\cdot \left( \frac{1}{2}\vec{a}-\vec{b} \right) = 0 \\
& \frac{1}{2}\left(\frac{t}{2}-1\right)|\vec{a}|^2+\left(-\left(\frac{t}{2}-1\right) -\frac{1}{2}(t-1)\right)\vec{a}\cdot\vec{b}+(t-1)|\vec{b}|^2=0\\
& \frac{1}{2}\left(\frac{t}{2}-1\right)\times 4+\left( -t+\frac{3}{2}\right)\times 3+(t-1)\times 9=0\\
& t-2-3t+\frac{9}{2}+9t-9=0\\
& 7t =\frac{13}{2}\\
& t =\frac{13}{14} \quad \cdots (答)\\
\end{split}
\end{equation}
$$

冒頭で予想していた1よりも少し小さくなりそうという見立てとも合致しましたね。

2.2【問題2】ベクトルの成分計算の利用

問題[福岡大　類題]

$\small \overrightarrow{OA}=(2,1)$、$\small \overrightarrow{OB}=(x,1)$とし、点Bから直線OAに下した垂線の足をHとするとき、$\small \overrightarrow{AH}=\left(-\frac{1}{2},-\frac{1}{4}\right)$となるような$\small x$の値を求めよ。

解答

$\small x=\frac{11}{8}$

解説

問題の文章を図式化すると以下の通り。

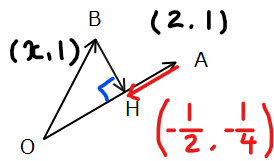
次に「垂線」というキーワードから、$\small \overrightarrow{BH}\cdot\overrightarrow{AH}=0$を解くことにしましょう。

とはいえ、$\small \overrightarrow{BH}$が分からない状態なので、まずはベクトルの分解をします。基点を点Oとすると、$\small \overrightarrow{BH}=\overrightarrow{OH}-\overrightarrow{OB}$となります。

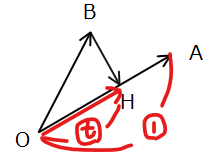
ここで、分解して出てきた$\small \overrightarrow{OH}$は、上図のように$\small \overrightarrow{OA}$と平行なので、$t$倍することで、$\small \overrightarrow{OH}=t\overrightarrow{OA}$と表すことができます。成分表示で表すと

$$\overrightarrow{OH}=t\overrightarrow{OA}=t(2,1)=(2t,t)$$

よって、$\small \overrightarrow{BH}$は、

$$
\begin{equation}
\begin{split}
\overrightarrow{BH}&=\overrightarrow{OH}-\overrightarrow{OB}\\
& = (2t,t)-(x,1)\\
&=(2t-x,t-1)
\end{split}
\end{equation}
$$

これを使って$\small \overrightarrow{BH}\cdot\overrightarrow{AH}=0$を計算すると、

$$\overrightarrow{BH}\cdot\overrightarrow{AH}=0$$

$$(2t-x,t-1) \cdot \left(-\frac{1}{2},-\frac{1}{4}\right) = 0$$

$$-\frac{1}{2}(2t-x)-\frac{1}{4}(t-1) = 0$$

$$2(2t-x)+(t-1) = 0$$

$$2x=5t-1$$

$$x=\frac{5t-1}{2}\quad\cdots①$$

あとは$t$の値が求まれば、$x$の値が分かります。何か使えそうな条件はないでしょうか。

行き詰ったときは、解説編で紹介したベクトル問題の基本的な考え方に立ち返ってみましょう。すると、ベクトル$\small \overrightarrow{AH}$だけ、基点Oからのベクトルになっていなかったことに気が付くでしょう。$\small \overrightarrow{AH}$の成分は分かっていますが、基点からのベクトルに分解してみます。

$$
\begin{equation}
\begin{split}
\overrightarrow{AH}&=\overrightarrow{OH}-\overrightarrow{OA}\\
& = (2t,t)-(2,1)\\
&=(2t-2,t-1)
\end{split}
\end{equation}
$$

これが、問題にあるように$\small \overrightarrow{AH}=\left(-\frac{1}{2},-\frac{1}{4}\right)$になるのですから、当然に成分同士が一致するはずです。$\small x$成分、$\small y$成分どちらでもよいのですが、計算が単純そうな$\small y$成分を比較することで、$\small t-1=-\frac{1}{4}$ → $\small t=\frac{3}{4}$と求まります。

よって、式①に代入することで、$\small x=\frac{5t-1}{2}=\frac{5\cdot\frac{3}{4}-1}{2}=\frac{\frac{11}{4}}{2}=\frac{11}{8}\cdots$(答)。