今回は、2次不等式の解き方をパターンごとに解説していきます。基本的な問題から、少し特殊な問題まで、本記事を一通り読めば2次不等式はマスターできる内容になっているので、ぜひ最後まで確認してみてください!
本記事のレベル
2次不等式の解き方
実は、2次不等式を解くときにやるべきことはたった1つしかありません。
それが以下のポイントになります。
2次不等式の解き方
2次不等式は、グラフをかいて、x軸の上か下かを見極めろ!
グラフを描く?x軸の上?下?…と思うかもしれませんが、この意味は例題を通して説明します。
解き方の解説(基本編)
例題1
以下の2次不等式を解け。
(i)\(\small x^2-7x+10>0\)
(ii)\(\small x^2-4x+3≦0\)
解答
(i)2次不等式を解く際には2次関数のグラフを描くとわかりやすいです。では、なぜ?というお話をします。
一旦、2次不等式は忘れて\(\small y=x^2-7x+10\)の2次関数を考えます。このグラフは書けますか?
ここではあまり詳しく話しませんが、平方完成すると、\(\small y=(x-\frac{7}{2})^2-\frac{9}{4}\)となり、頂点が\((\small \frac{7}{2},-\frac{9}{4})\)などの情報が分かります。平方完成、地味に面倒くさいですよね。でも、安心してください。今回は、頂点の座標を求める必要はありません。必要なのは、x軸との交点の座標です。どうやって求めますか?グラフがx軸と交わるときは、必ずy座標は0ですよね?なので、\(\small y=x^2-7x+10\)にy=0を代入してxを求めてあげれば、x軸との交点の座標が求まります。\(\small x^2-7x+10=0\)を解く…あれ、よく見ると、これは2次方程式ですよね?つまり、2次関数でx軸との交点を求めたい場合は、2次方程式を解けばよいことが分かります。
$$\small x^2-7x+10=0$$ $$\small (x-2)(x-5)=0$$ $$\space\space\space\space\space\space\space\space\space\space\space\space\space\small x=2,5 ※これがx軸との交点$$
なので、下図のようなグラフが書けます。このグラフがめちゃくちゃ大事です!
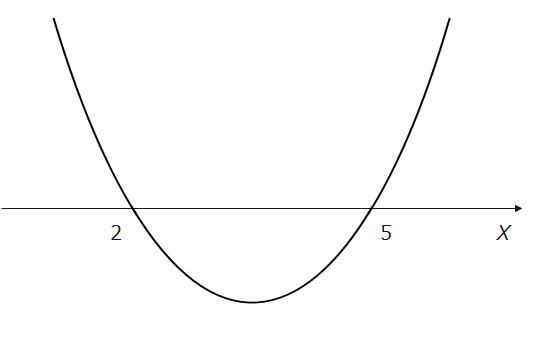
ここで、本題の2次不等式、\(\small x^2-7x+10>0\)を見てみましょう。2次不等式の左側は、今グラフを描いた、2次関数ですね。そしてこの2次関数は、\(\small y=x^2-7x+10\)なので、\(\small x^2-7x+10>0\)は、 $$\small y>0$$ と簡単に表すことができます。では、この式は何を表しているでしょうか?不等式をそのまま言葉に訳すと、
「yは0より大きい」と読めます。つまり、2次関数、\(\small y=x^2-7x+10\)のyが0より大きい部分ですよ、ということです。式だと全然意味が分かりませんが、グラフを見ると、yの値がが0より大きい部分は、すなわちx軸の上側だとすぐにわかりますね。色付けするならば、下の図の赤の部分です。
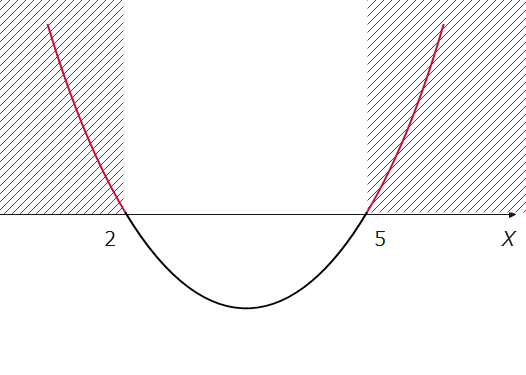
この図から、xの範囲は、 \(\small x<2,5<x\space\cdots\)(答)
(ii)では、こちらもグラフを描くことから始めましょう。まずは2次関数、\(x^2-4x+3=0\) をといて、x軸との交点を求めます。
$$x^2-4x+3=0$$ $$(x-1)(x-3)=0$$ $$x=1,3$$ よって、グラフは左下図になります。
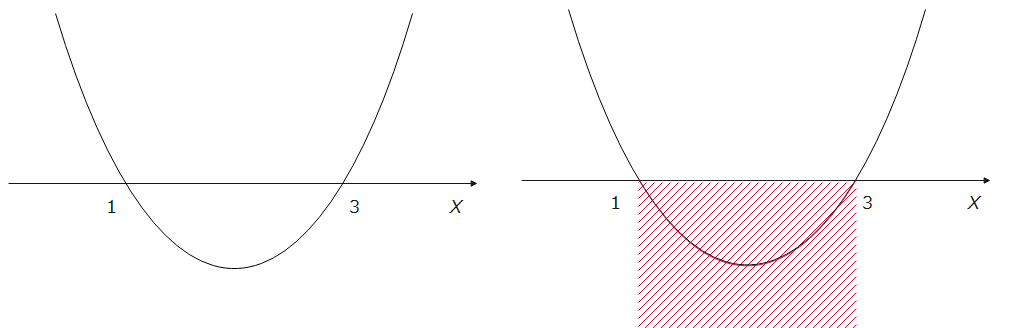
あとは、x軸の上なのか、下なのかを見極めるだけですね。今回の問題は、\(\small x^2-4x+3<0\)なので、左側の2次関数を\(y\)として見てあげると、\(\small y≦0\)、訳すと、「yは0以下」なので、yの値が0以下なのは、x軸の下側ですね。よって、右上図で赤くなっている部分が答えなので、\(\small 1 ≦ x ≦ 3\space \cdots\)(答)
2乗の係数がマイナスの場合
例題2
以下の2次不等式を解け。
\(\small -x^2+x+6>0\)
解答
解き方は2パターンあります。まずは、例題1と同じように、x軸との交点を求めていきます。
$$\small -x^2+x+6=0$$ $$\small x^2-x-6=0$$ $$\small (x+2)(x-3)=0$$ $$\small x=-2,3$$
図としては、右のようになります。今回は、\(x^2\)の前にマイナスがついているので 例題1の時とは上下がさかさまになるんでしたね。忘れていた人は2次関数の性質をおさらいしておきましょう!
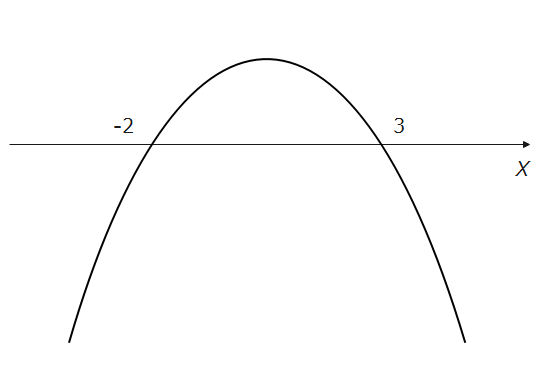
さて、2次不等式に戻って、x軸より上か下かを確認しましょう。
\(\small -x^2+x+6>0\)なので、\(\small y>0\)を見ると、x軸の上側なので、答えは、赤色の範囲。
$$\small -2 ≦ x ≦ 3\space \cdots(答)$$
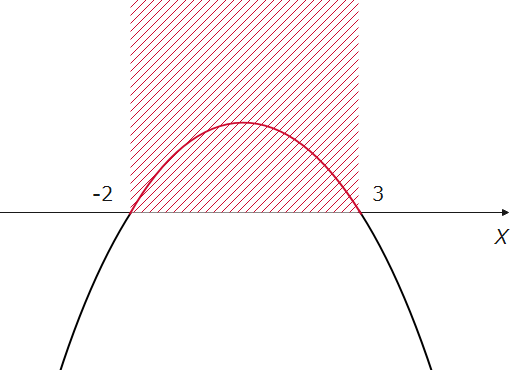
このように、解くこともできますが、上下がさかさまになるところが、忘れてしまう可能性もあり、毎回上下を意識して解くのも大変ですよね。なので、個人的には、\(x^2\)の前にマイナスがついている場合は、初めに消すことをお勧めします。消し方は、全体にマイナスを掛け算して、\(\small x^2-x-6<0\)とするだけです。この時に、不等式の向きが変わるので注意しましょう。あとは、例題1と同じように図を描くと同じ答えになります。図を参考までに載せておきます。今回は不等号の向きが変わってるので、y<0でx軸の下側が求める範囲になっています。
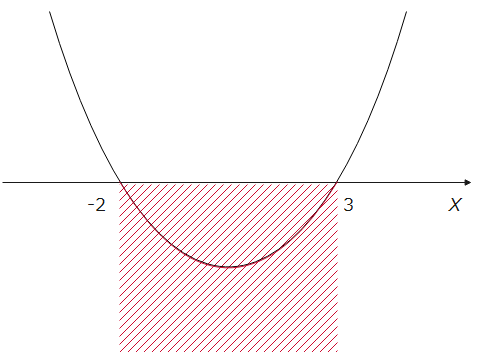
解の公式を利用する場合
例題3
以下の2次不等式を解け。
\(\small x^2+x-3>0\)
解答
同じように解いていきましょう。まずはx軸との交点を求めるために2次方程式を解くんでした。
今回は因数分解ができないので、解の公式を使います。すると、\(x=\frac{-1 \pm \sqrt{13}}{2}\)と求まるので、ごつい解 ですが、この2点がx軸との交点です。グラフは慣れてきたら書かなくてもOKです。今回の問題では\(\small y > 0\)なので、x軸の上側が求める範囲なので、2つの範囲に分かれるパターンですね。
よって、\(\small x < \frac{-1 – \sqrt{13}}{2}, \frac{-1 + \sqrt{13}}{2} < x \space \cdots\)(答)
特殊パターン4選
例題4
以下の2次不等式を解け。
(i)\(\small x^2+4x+4>0\)
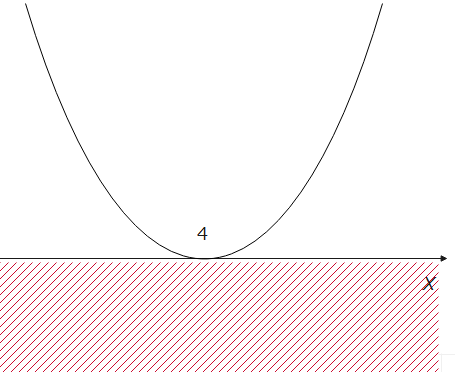
(ii)\(\small x^2-8x+16<0\)
(iii)\(\small x^2+6x+9≦0\)
(iv)\(\small x^2-3x+10>0\)
解答
ここからは特殊なパターンです。引っかからないように注意しましょう。 (i)2次方程式、\(\small x^2+4x+4=0\)を解くと、\(x=-2\)となります。普通、2次方程式の解は2個(交点が2個あるので)ですが、今回みたいに1個だけになる場合があります。この時は、グラフとしては、x軸との交点が1個のみということなので下図のように2次関数はx軸に接している状態となります。
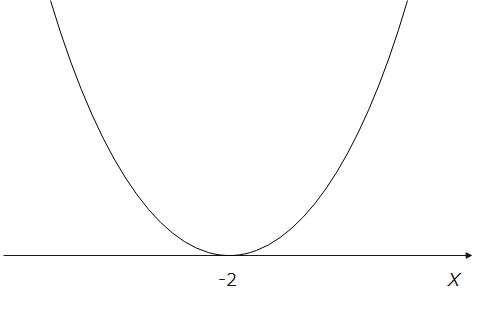
よって、該当範囲は、x軸の上側なので、以下の図から、すべての実数!…と思った方、残念。惜しいですが、違います。不等号に注目してください。
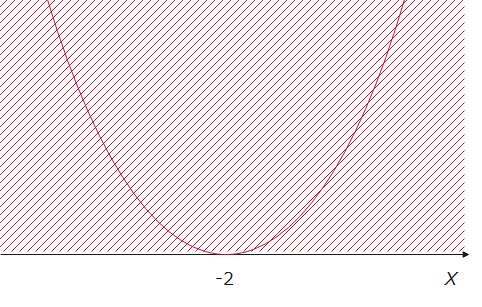
今回は、0より大きいなので、0(つまりx軸)は含まれません。下図のグラフのほとんどはyが0より大きいですが、1点だけ、0になっている部分があります。そうですね、x軸との交点である\(\small x=-2\)です。よって、答えとしては、 \(\small x=-2\) を除くすべての実数。\(\cdots \)(答)となります。
(iii)2次方程式、\(\small x^2+6x+9\)の解は\(\small x=-3\)です。グラフは、下図のようになり、今回は不等号にイコールが含まれているので、x軸を含む下側が該当範囲になります。
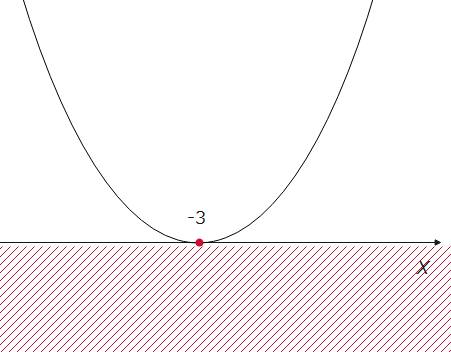
一見、赤色の範囲内にグラフ上の点がないので、解なしかと思うかもしれませんが、x軸上も含まれるので、x軸上にある、\(\small x=-3\)はぎりぎり赤枠の範囲内です。よって、答えは、\(\small x=-3\)\(\cdots\)(答)です。
(iv)この問題は一見すると前の3問と同じように解けそうです。まず2次方程式、\(\small x^2-3x+10=0\)を解きますが、 因数分解できなさそうなので、解の公式で求めます。
\(x=\frac{-b \pm \sqrt{b^2-4ac}}{2a}\)にあてはめると、\(x=\frac{3 \pm \sqrt{9-4×1×10}}{2}=\frac{3 \pm \sqrt{-31}}{2}\)となりますが、ルートの中身がマイナスになってしまいました。ルートの中身がマイナスになることはないので、今回の2次方程式の答えは解なしとなります。まだ、2次不等式の答えではないので、気を抜かないでくださいね…。2次方程式の解がないというのはグラフ的にはどういう意味でしょう?解が2個ならばx軸と2点で交わる、解が1個ならば、x軸と1点で接する…、ということは、解がない場合は、x軸と交わらないということになりますね。図で書くと下図のような感じですね。

グラフが描けさえすれば、あとは同様にx軸の上か下かを見ていきますが、今回は\(\small y>0\)、つまりx軸よりも上側です。 よって、グラフ上のすべての部分で条件を満たしているので、答えは、すべての実数。\(\cdots\)(答)となります。
まとめ
今回は、2次不等式の基本パターンといくつかの特殊パターンを見ていきました。どの問題も、2次方程式を解いて、グラフを描いた後に、x軸の上側 or 下側を満たすグラフ上の部分がどこなのかを考えるという手順で解けましたね。不等号の向きなどでパターン化して解答する考え方もありますが、いろいろと落とし穴があるのと、応用問題になった際に太刀打ちできなくなってしまうので、今回の考え方をしっかりとマスターして頭に叩き込んでおきましょう。次回はもう少しレベルアップした問題に挑戦していきましょう。







コメント