今日は円周率についてお話します。
誰もが一度は聞いたことがある円周率。では、質問です。
円周率って何でしょうか?
3.141592…と永遠に続く数といった回答が多いのではないかなと思います。もちろん、それも正解ですが、ではその数字って何を表しているのでしょうか。意外とこの質問に正しく答えられる人は少ないのではないと思います。
誰もが小学校の時に円周率は、3.14だと暗記して、円周率を使って円の面積やら円周やらを求めるために使ってきましたが、そもそも何なのかといった部分はあまり取り上げられていないことが多いです。今日はそんな円周率について、お話していこうと思います。
円周率とは
結論、円周率とは以下のように定義されています。
ちょっと言葉で言われてもピンとこないですよね。
簡単に言うと、「円の周りの長さが直径の何倍になるのか」を表しているが円周率だ、ということです。円周率はみなさんご存じ、約3.14なので、円周は直径の約3.14倍だよということを表していることになります。どうですか?円周率の意味が分かると、3.14という数字の持つ意味がイメージできたのではないでしょうか。このように、用語には必ず意味があるので、用語の意味まで理解することが実はとても重要です。
円周率から円周へ
円周率は、直径に対する円周の比率といいましたが、確かに円周に関する比率ということでそりゃそうですね。ただ、この円周率が分かると円についていろいろなことが分かってきます。何が?と思った方もいると思いますが、先程、円周は直径の約3.14倍だといいました。
例えば、直径が2cmの場合、円周はいくつでしょうか。約3.14倍なので約6.28cmですね。直径が10cmであれば、10cm×3.14で、約31.4cmです。円周を求めたければ、直径に円周率をかければ求められることが分かります。これは、皆さんが小学校で学んだ円周の求め方の公式ですね。
円周 = 直径 × 3.14(円周率) (式1)
こんな風に、円周率とは何かを知っておけば、そこから少し考えるだけで円周の求め方まで分かってしまいました。円周の公式は忘れないかもしれませんが、数学で出てくるたくさんの公式も同じように基本を押さえておけばそこから導き出せるんです。
円の面積の求め方
円周を求めたので続いて円の面積を考えてみましょう。
皆さん公式は覚えていますか?こちらは少し複雑ですね。
円の面積 = 半径 × 半径 × 3.14(円周率)
では、なんでこれで面積が求められるのでしょうか。詳しい説明は高校数学で習う積分にお任せするとして、ここでは感覚的にわかった気分になることを目的に説明していきますね。
以下の図のように、円を半分に切り刻んでいきます。そして図の赤色の部分と青色の部分をがばっと開いて、かみ合わせます。今回は円を16等分にしかしていないので微妙ですがもっと多く分割をすることで完全な長方形になります。
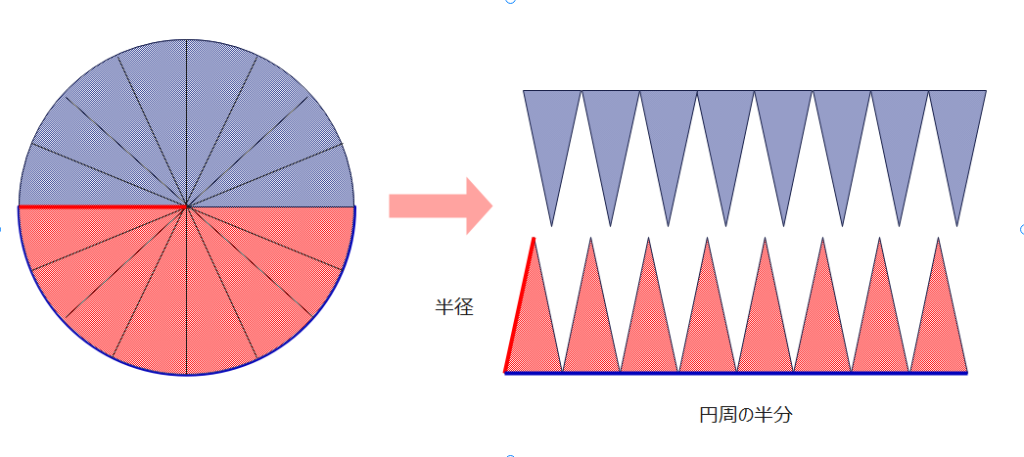
図を見ると、縦の長さはもともとの円の半径で、横の長さは、円周の半分なので式(1)より、
円周の半分 = \(\frac{円周 }{2} \)= \(\frac{直径 × 3.14(円周率)}{2}\) = \(\frac{直径}{2} \)× 3.14(円周率)
\(\space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \) =半径 × 3.14(円周率) (式2)
最後の式変形では直径の半分は半径はので、言葉を置き換えました。
よって円の面積は、図の長方形の面積なので
円の面積 = 半径 × 円周の半分
\(\space \space \space \space \space \space \space \space \space \space \space \space \space \) = 半径 × 半径 × 3.14(円周率)
となります。(式2)の結果を代入しています。
割と強引に説明しましたが、イメージは沸いたのではないでしょうか。
円を分割しまくったら長方形になるという理論はやや強引ですが、本当に長方形として考えてよいのかについては、もっと難しい数学の知識が必要になるので、いったんはこの程度の理解でも良いかと思います。
ということで、今回は円周率とは何かというところから、円周や円の面積の求め方まで導いてみましたが、いかがだったでしょうか。内容的には小学生で習う算数でしたが意外と何でこんな公式なのかという部分までは考えたことがなかったのではないでしょうか。
ただ暗記するだけではなく、たまにはどうしてこんな公式になるんだっけと考えてみると数学力だけでなく思考力もアップすると思うので、改めて身の回りの公式を見つめなおしてみるのも良いのではないでしょうか。





コメント