【数学オリンピック】n+2024、n-34の各桁が素数になる3桁の整数nを求めよ（予選問題（2024））

本記事では数学オリンピックの予選問題（2024年）の中から面白い問題をいくつか紹介していきたいと思います。個人的には数学オリンピックに出題される問題は、受験数学とはまた違った頭の使い方や数学的センス・勘的なものが求められる気がしているので、いろいろな問題を解いて数学の面白さを感じていければと思っています。

また、最後の方の問題は数オリ受験者のような数学の猛者たちが集まった中でも正答率が圧倒的に低いようなので、正直私に解ける気はしませんが、どのレベルまで解くことができるのかも併せて検証していきたいと思いますので、皆さんも一緒にどこまで解けるのかぜひチャレンジしてみてください！

【数学オリンピック】予選問題（2024年）
本記事のまとめ
1. 【類題1】有理数になる条件
2. 【類題2】”素敵な数”の個数を求めよ

【数学オリンピック】予選問題（2024年）

【問題1】階乗を含む分数計算

以下の値は有理数である。これを既約分数の形で表せ。
$$\small \displaystyle \sqrt{\frac{123!-122!}{122!-121!}}$$

　解説

階乗の差なのでうまく共通項を括り出せばいけそうな感覚。

実際に計算してみると…

\begin{split}
&\small \sqrt{\frac{123!-122!}{122!-121!}}\\
\small = &\small \sqrt{\frac{\color{red}{123 \cdot 122!}-122!}{\color{red}{122 \cdot 121!}-121!}}\\
\small = &\small \sqrt{\frac{122!(123-1)}{121!(122-1)}}\\
\small = &\small \sqrt{\frac{122!\cdot 122}{121!\cdot 121}}\\
\small = &\small \sqrt{\frac{122\cdot 121!\cdot 122}{121!\cdot 121}}\\
\small = &\small \sqrt{\frac{122^2}{11^2}}\\
\small = & \color{red}{\small \frac{122}{11}\quad \cdots【答】}\\
\end{split}

まとめ

ひたすらに$\small n!= n \cdot (n-1)!$の関係を利用して約分をしていくとすっきりした形に整理できるという問題でしたね。

【問題2】”素敵な数”に関する問題

どの桁に現れる数字も素数であるような正の整数を素敵な数とよぶ。3桁の正の整数$\small n$であって、$\small n+2024$と$\small n-34$がともに素敵な数であるものはちょうど2つある。このような$\small n$をすべて求めよ。

　解説

さて、数学オリンピックでは頻出の整数問題ですね。しかも、数Ⅰで出てくるような整数問題とは異なり、「“素敵な数”を特定の数式で表せない」という点がかなり厄介です。

ただ、幸いなことに求めるべき3桁の正の整数$\small n$は2つしかないと問題文で言ってくれているので、とりあえず勘でもいいから2つ見つければOKということです。

しらみつぶしに探すには数が多すぎるので、問題文の条件である$\small n+2024$と$\small n-34$が各桁が素数になるというヒントを手掛かりに求める$\small n$の3桁の数字を絞り込みしていきましょう。

[1]$\small n$の1の位
$\small n$の一の位は0～9までの10パターンあるので、それぞれに対して$\small n+2024$と$\small n-34$を計算した結果、1の位が素数（2,3,5,7）になるかを確認しておきます（下の画像で1の位が0のパターンを忘れてました…。でも1の位が0の場合は$\small n+2024$の1の位が4で素数ではないのでダメですね）。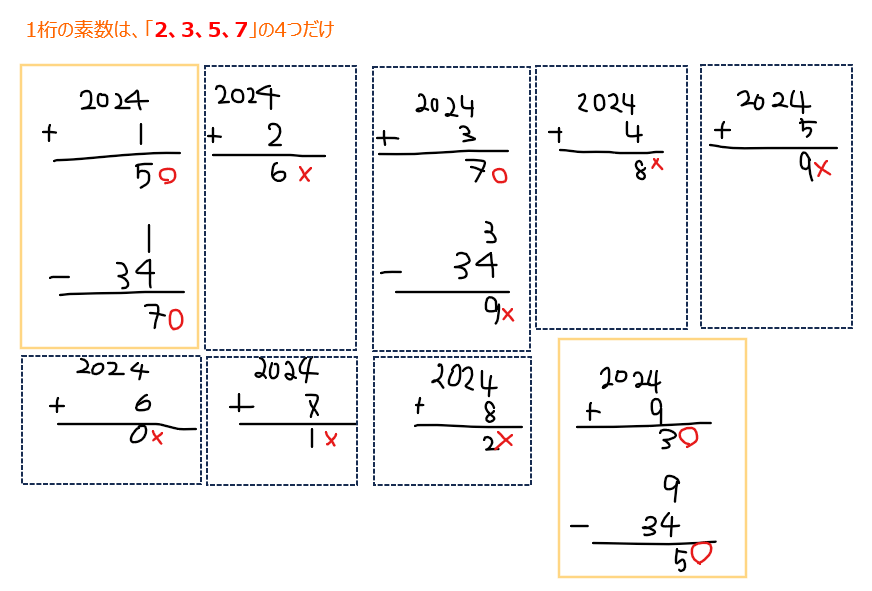

これらの結果から、$\small n$の1の位としては1か9しか取り得ないということが分かります（意外と絞り込めました！）。

ということで次は十の位を見ていきましょう。

[2]$\small n$の十の位
まず、1の位が1の場合の十の位として取り得る数字は、2024との足し算の結果が素数にならないといけないので、「0、1、3、5」の4択。そのうち、34との引き算も素数になるパターンは十の位が1の場合のみです。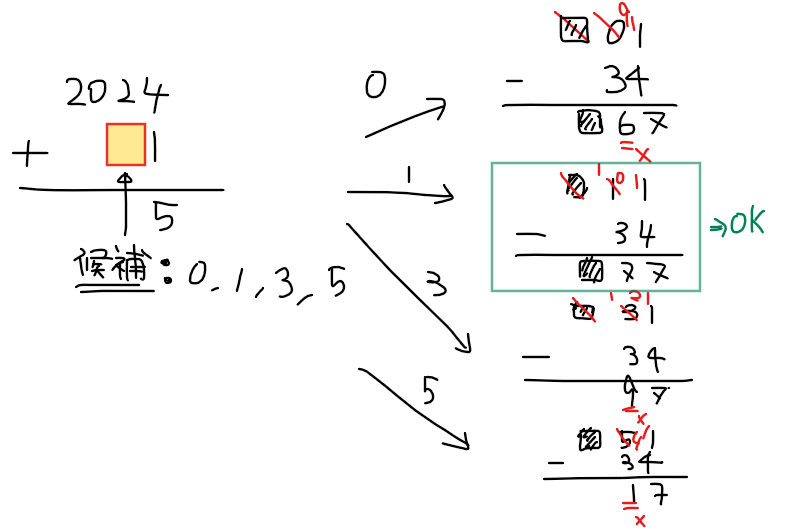

同様に1の位が9のときも考えると、2024との足し算の結果が素数になることから十の位が取り得る値は「０、2、４、９」の4択です（4+9の繰り上がりの1があることに注意)。そのうち34との引き算も素数になるのは十の位が0の場合のみです（実際に計算して確かめてみると分かります）。

ここまでの結果を整理すると、$\small n$の候補としては、「■11」と「■09」の2つというところまで絞れました。あとは、それぞれ9択なのでローラーしてもよいでしょう。

実際に計算すると「311」と「309」が答えになります。

まとめ

各桁が素数となる数字は数式では表せない＝数式的には解けないので、実際に手を動かして計算していくことで答えを探していく必要がある問題でした。答えを探す際にポイントになるのが、【答えの絞り込み方】で、やみくもに考えるのではなく「こうなっていないといけない」というポイント（手掛かり）をうまく見つけて絞り込みする力が問われているのかなと思います。

【問題3】図形問題

一辺の長さが10の正三角形$\small ABC$がある。$\small A$を通る円が辺$\small BC$（端点を除く）と点$\small X$で接し、辺$\small AB,AC$とそれぞれ$\small A$でない点$\small D,E$で交わっている。$\small BX>CX,AD+AE=13$がともに成り立つとき、線分$\small BX$の長さを求めよ。ただし、$\small PQ$で線分$\small PQ$の長さを表すものとする。

　解説

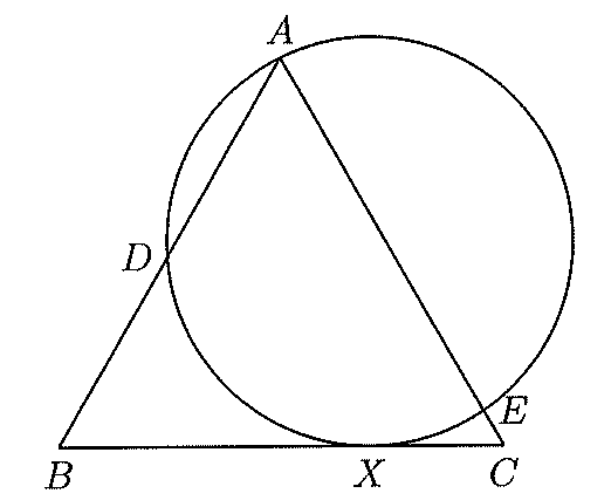
今回の図形問題では、点$\small X$が円の接点になっていることから、方べきの定理を利用する問題だと推測できます。

●補足：方べきの定理とは？
方べきの定理については、こちらの記事が分かりやすいので不安な人は確認しておきましょう。
方べきの定理の意味と2通りの証明

なので、分からない辺を下図のように$\small x,y$とおいて、方程式を立てて解く方針で考えてみましょう（今回求めるのは$\small x$の値）。

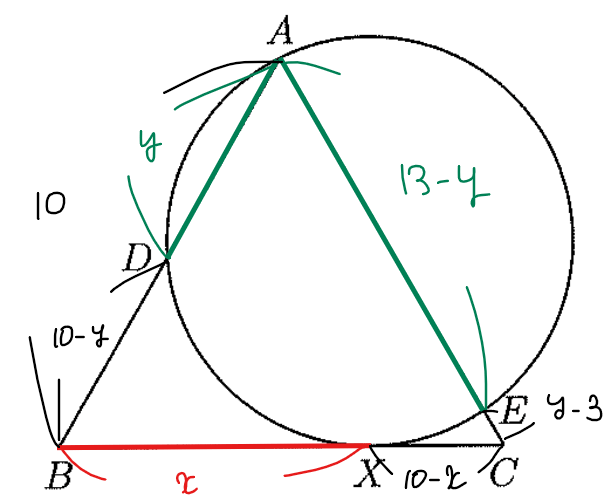
方べきの定理より

\begin{split}
\small &\small BX^2 =BD\cdot BA\\
\small \Leftrightarrow \space &\small x^2 =10(10-y) \space \cdots ①\\
\end{split}

\begin{split}
\small &\small CX^2 =CE \cdot CA\\
\small \Leftrightarrow \space &\small (10-x)^2 =10(y-3)\\
\small \Leftrightarrow \space &\small 10-y = 7-\frac{(10-x)^2 }{10} \space \cdots ②\\
\end{split}

●補足
②の式は普通に$\small y$について解いて①に代入してもよいですが、①の右辺に代入しやすいように$\small 10-y$の形にしておくと計算が楽です。

②を①に代入することで

\begin{split}
&\small x^2 =70-(x-10)^2\\
&\small x^2 -10x+15=0\\
&\small ∴ \space x=5 \pm \sqrt{10}\\
\end{split}

ここで、問題の条件から$\small BX>CX$なので、$\small BX$の方が長い、すなわち辺$\small BC$の半分の長さ5よりも長いことから、$\small \color{red}{BX = 5 + \sqrt{10} \space \cdots 【答】}$と求まります。

●補足
最後に解が2つ出てきたのは問題の図形を左右反転した図形の場合があるからですね。

まとめ

図形問題かと思いきや方べきの定理を利用して方程式を解く良問でした。このレベルであれば大学入試や数Aの定期試験に出てもおかしくなさそうですね。

本記事のまとめ

ということで、今回はここまでです。数学オリンピック2024年予選問題の最初の3問を解説していきましたが、個人的には問題2が結構大変でしたね。他にも皆さんの感想や別解などもあればぜひコメント欄に記載をお願いします。

次回は問題4以降に挑戦していきますが、ここから一気に難易度が上がり大変になってきそうな印象ですが、なかなか解きごたえがありそうなので、引き続き頑張ってみようと思います。

最後に復習がてらに今回解説した数学オリンピックの類題を作ってみたので、皆さんも解けるかぜひ挑戦してみてください！

【類題1】有理数になる条件

$\small n$を1以上の整数とするとき、$\small \displaystyle \sqrt{\frac{(n+1)!-n!}{n!-(n-1)!}}$が有理数になるための条件を述べよ。

　解説

\begin{split}
\small \displaystyle \sqrt{\frac{(n+1)!-n!}{n!-(n-1)!}} &\small \displaystyle =\sqrt{\frac{n!\cdot n}{(n-1)!(n-1)}}\\
&\small \displaystyle =\sqrt{\frac{n^2}{(n-1)}}\\
&\small \displaystyle =\frac{n}{\sqrt{(n-1)}}\\
\end{split}

よって、分母にあるルートが消えれば有理数となることから、$\small n-1$が平方数になること…【答】。