今回は、正弦定理について解説します。いつも正弦定理を忘れちゃうという人には必見の覚え方も紹介しているので、今一度正弦定理について見直していきましょう。
はじめに
図形の分野で三角比を習った後に出てくるのが正弦定理と余弦定理です。この2公式は図形の分野では頻出の絶対に忘れてはいけない公式です。そんな2公式のうち、今回は正弦定理の攻略法として覚えるべきなのか、理解するべきなのか含めて解説していくので、ぜひ最後まで読んでみてください!
★本記事で扱う公式
正弦定理とは
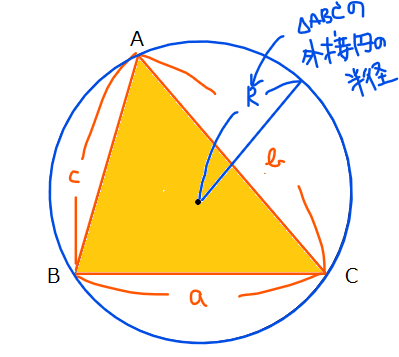
正弦定理のスペック
★正弦定理の攻略法
正弦定理は暗記せよ
早速、本記事の結論ですが、正弦定理は「暗記」一択です。理由としては、
- 使用頻度が高く、いちいち導出するのが面倒くさい
- 導出方法も図形的センスが必要であり意外と難しい
の2点があげられます。
使うたびに導出は意外と難しく大変
ここで、参考までに正弦定理の導出方法を解説します。
なお、ここでは導出の雰囲気を掴んでもらうことが目的のため、角度Aが鋭角の場合の証明のみを記載しています。本当は角度が直角の場合、鈍角の場合の証明も必要ですが今回は割愛しているのでご注意ください。
■正弦定理の導出方法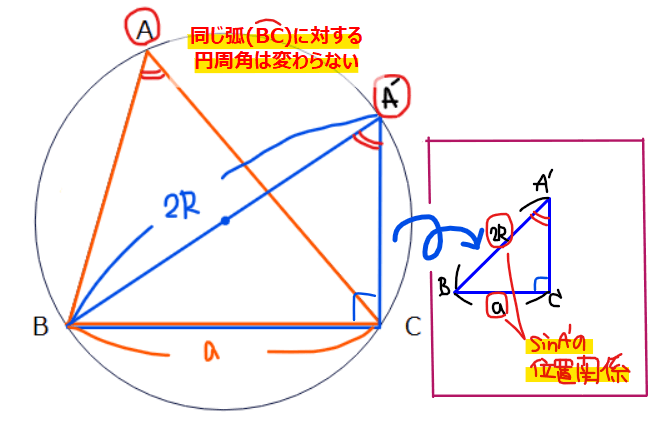
$$
\begin{equation}
\begin{split}
&\sin A =\sin A’ \quad \text{※同じ弧に対する円周角は変わらない}\\
&\qquad \space=\frac{a}{2R}\\
⇔\quad & \sin A=\frac{a}{2R}\\
⇔\quad &2R=\frac{a}{\sin A}
\end{split}
\end{equation}
$$
こんな感じで導出できますが、簡単ではないですよね?
「もしこの導出暗記できます!」という人がいれば毎回導出もOKかもしれませんが、使用頻度も高いこと、ほとんどの人が導出方法を忘れてしまうと思うことから、この導出を覚えるくらいなら公式自体を暗記したほうがてっとり早いかなと思います。
簡単に暗記するコツ
ここで極力暗記したくない皆さんからは、「暗記が必要なのは分かったけどどうやって覚えればいいの?」、「暗記しやすい工夫はないの?」といった声が聞こえてきそうなので、ここからは、私個人の覚え方を解説していきます。
正弦定理は2種類に分けて暗記する
正弦定理を実際に問題で使うときは以下の2パターンのどちらかになると思うのでそれぞれで分けて暗記するのがおすすめです。
■パターン1:辺や角度を求めるとき
$$
\begin{equation}
\begin{split}
&\color{red}{\frac{〇}{\sin 〇}=\frac{△}{\sin △}}\\
&\textrm{※〇、△には、辺なら}a,b,c、\textrm{角度なら}A,B,C \textrm{を入れる}
\end{split}
\end{equation}
$$
■パターン2:外接円の半径を求めるとき
$$
\begin{equation}
\begin{split}
&\color{red}{\frac{〇}{\sin 〇}=2R}\\
&\textrm{※〇、△には、辺なら}a,b,c、\textrm{角度なら}A,B,C \textrm{を入れる}
\end{split}
\end{equation}
$$
パターン1:辺や角度を求める用
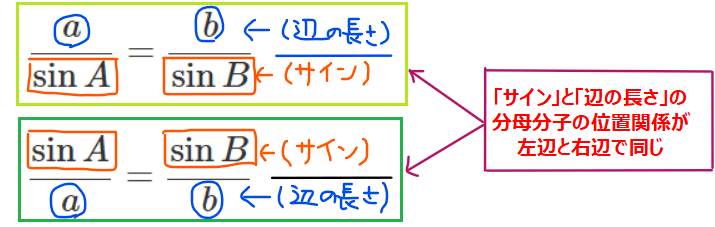
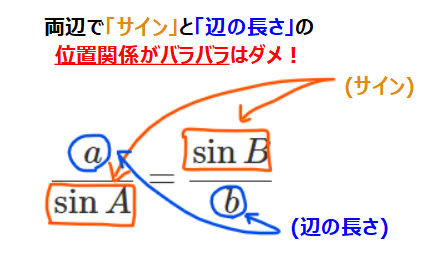
この公式は、『「サイン」と「辺の長さ」を分数にしたら同じになる』と覚えればokです。
「サインと辺の長さのどっちが分母だったっけ?」と迷った時でも、左辺と右辺で「サイン」と「辺の長さ」の「分母分子の上下関係」だけ揃えておけば、分母分子が逆になってもイコールが成立します。どういうことか具体的にいうと、
$$\frac{a}{\sin A}=\frac{b}{\sin B}$$
でも
$$\frac{\sin A}{a}=\frac{\sin B}{b}$$
でも、どちらでもokということです。
まぁ、分数なので分母分子を逆にしてもイコールは成り立つので当たり前ですが…。ただ、この当たり前が暗記においては結構便利です。正弦定理で「サインの値」と「辺の長さ」が必要なのは覚えてるけど分母と分子がどっちだったかな…という不安は結構あります。この時に、どっちでも問題ないというのはそれだけで安心材料になるので、しっかり押さえておきましょう。
パターン2:外接円の半径を求める用
正弦定理を使うもう一つの場面が、△ABCの外接円の半径\(\small R\)を求めるときです。パターン1の公式は、分母分子を覚えてなくても、左辺と右辺でサインと辺の長さの上下関係だけ揃えておけば攻略できました。一方で
$$\frac{〇}{\sin 〇}=2R$$
の公式は、右辺が分数ではないので、そう簡単にはいきません。
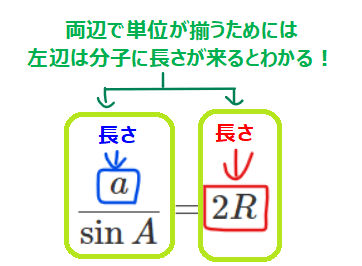
では、どう覚えればいいのか?答えは、「右辺と左辺で単位は揃う」という知識を知っていれば、左辺の分母と分子を間違えることはありません。
どういうことかというと、物理をやっている人はピンとくるかもしれませんが、公式の左辺と右辺では必ず「単位」が揃うという性質があります。難しく聞こえますが、要は左辺が重さ(kg)なら右辺も重さ(kg)だよねって話です。逆に、左辺が時間(秒)なのに右辺が電力(W)なんてことはありませんよね?
これはもちろん数学にも当てはまります。今回の正弦定理でいうと、右辺は「\(\small 2R\)」なので半径の2倍=直径です。これは長さを表しています。ということは、左辺の「\(\small \frac{a}{\sin A}\)」なども長さを表しているわけです。ここでもし、「左辺が\(\small \frac{a}{\sin A}\)、\(\small \frac{\sin A}{a}\)のどっちだったかな?」と忘れてしまったら、左辺も長さになるはずなので分子には長さを表す「\(\small a\)」が来るはずだ、と分かります。なので、左辺は\(\small \frac{a}{\sin A}\)が正しいと分かるわけです。ちなみに、\(\small \sin A\)は三角比、つまり単なる比なので単位はありません。
こんな風に単位が両辺で同じになるという性質を知っていれば分母と分子を忘れてしまっても導き出すことができるので、ぜひ覚えておきましょう!
まとめ
今回は正弦定理について解説しました。公式自体は暗記がおすすめで、暗記のコツもパターンごとに攻略法を解説しました。今回紹介した暗記方法以外にも覚え方は人それぞれあると思いますが、いくつか紹介しておきます。暗記方法は自分が一番覚えやすい方法で覚えればよいので、もし参考になるものがあれば活用しちゃいましょう。
- サインが下(分母)と覚えておく。
- \(\small a:b=\sin A:\sin B\)と辺と三角比の比が一定と覚えてしまう。
(理由)
\(\small a:b=\sin A:\sin B\)
\(\small a\sin B=b\sin A\) ※内項の積=外項の積
\(\small \dfrac{a}{\sin A}=\dfrac{b}{\sin B}\)
本日はここまでです。お疲れさまでした!