【軌跡】もう迷わない！軌跡の問題を解く基本の3ステップ【図形と方程式】

　本記事のレベル

　奇跡の求め方　～基本の3step～

点\(\small K(x,y)\)が\(\small x^2+y^2=2\) 上を動くとき、\(\small L(2x+y+1,-x+2y-1)\)の軌跡を求めよ。

上の基本stepにあてはめて解いていきましょう。
★step1：求める点を\(\small (X,Y)\)とおく。
今回求めるのは点\(L\) なので、\(\small X=2x+y+1\)、\(\small Y=-x+2y-1\) とおきます。

★step2：動く点と条件をパラメータ化する。
軌跡の問題では、ある点がある条件を満たすとき、どんな軌跡なるのかということが問われるので、今回の場合で言うと動く点が\(\small K(x,y)\) 、条件が\(\small x^2+y^2=2\) になります。パラメータで表すと聞くと、難しく感じるかもしれませんが、大体は動くものをパラメータでおけは良いです。今回だと点\(\small K\)を\(\small K(s,t)\)と置けばOK。点\(\small K\)は、\(\small x^2+y^2=2\) 上の点(つまり、この関係式を満たす)なので、\(\small s^2+t^2=2\) のように、条件式もパラメータで表せます。また、点\(\small K\)の座標\(\small x,y\)を\(\small s,t\)で置き換えたので、点\(\small L\)についても、step1の結果から、\(\small X=2s+t+1\)、\(\small Y=-s+2t-1\)としておきます。

★step3：パラメータを消去して、\(\small X,Y\)だけの式にする。
step2までの結果を整理すると、\(\small X=2s+t+1\)\(\cdots\)①、\(\small Y=-s+2t-1\)\(\cdots\)② 、\(\small s^2+t^2=2\)です。step3では\(\small s,t\)(パラメータ)を消去して、\(\small X,Y\)だけの式で表せばよいことになります。なので、①、②を\(\small s,t\)について解いて、\(\small s^2+t^2=2\)に代入すればよさそうですね。
①+②×2より、
\(\small X+2Y=5t-1\)
∴\(\small t=\frac{X+2Y+1}{5}\space\cdots\)③
③を①に代入して、
\(\small X=2s+\frac{X+2Y+1}{5}+1\)
\(\small 5X=10s+X+2Y+1+5\)
\(\small 10s=4X-2Y-6\)
∴\(\small s=\frac{2X-Y-3}{5}\space\cdots\)④
あとは③、④を\(\small s^2+t^2=2\)に代入すると
\(\small (\frac{2X-Y-3}{5})^2 + (\frac{X+2Y+1}{5})^2=2\)
\(\small (2X-Y-3)^2+(X+2Y+1)^2=50\)
\(\small 4X^2+Y^2+9-4XY+6Y-12X+X^2+4Y^2+1+4XY+4Y+2X=50\)
\(\small 5X^2+5Y^2-10X+10Y=40\)
\(\small X^2+Y^2-2X+2Y=8\)
\(\small (X-1)^2+(Y+1)^2=10\)
よって
\(\small (x-1)^2+(y+1)^2=10\space\cdots\)(答)

補足　なんで\(\small X,Y\)を(\(\small x,y)\)で置き換えるの？

例題1では、一旦、条件を満たすどこか特定の1点を\(\small X,Y\)と置いています。ただ、条件を満たす点は無数にあるので、これらの点をすべて表すことができるように、特定の点(\(\small X,Y\))ではなくて変数(\(\small x,y\))に置き換えてあげるのです。

点\(\small P(x,y)\)が\(\small y=x^2-5\) 上を動くとき、点\(\small A(1,0)\)と点\(\small P(x,y)\)の中点の軌跡を求めよ。

★step1
求める点は中点なので、中点の座標を\(\small M(X,Y)\)とおく。
★step2
動く点\(\small P(x,y)\)を\(\small P(s,t)\)とおくと、\(\small t=s^2-5\space\cdots\)① が成り立つ。
★step3
点\(\small P\)と点\(\small A\)の中点は、 \(\small (\frac{s+1}{2},\frac{t}{2})\) であり、これがまさしく中点\(\small M\)なので、step1で\(\small M(X,Y)\)とおいたことを思い出すと、
\(\small X = \frac{s+1}{2}\space\cdots\)②
\(\small Y = \frac{t}{2}\space\cdots\)③
②、③を\(\small s,t\)について解くと、
\(\small s = 2X-1\space\cdots\)④
\(\small t = 2Y\space\cdots\)⑤
④、⑤を①に代入すると、
\(\small 2Y = (2X-1)^2-5\)
\(\small 2Y = 4X^2-4X+1-5\)
\(\small Y = 2X^2-2X-2\)
∴\(\small y = 2x^2-2X-2\space\cdots\)(答)

\(\small xy\)平面上で、点(1,1)からの距離が2である点を点Pとするとき、点Pの軌跡を求めよ。

複雑に書いていますが、一点から等距離にある点の集合は円なので、要は点Pというのは中心が(1,1)の半径2の円を表しています。よって答えは、
$$\small (x-1)^2 + (y-1)^2 = 4$$ です。もちろんこのように、知識から解いてもよいのですが、最初に紹介した3stepを使って解いてみましょう。
まず、求める点Pを(\\small (X,Y)\)とおきます。次に動く点ですが、今回の場合は動くのも点\(P\)ですね。では、条件はどれでしょうか？文章中の「点(1,1)からの距離が2である点」が該当します。この文章を条件式として表すことを考えます。ちょっと難しいですが、下の図のように中心をC(1,1)とおいて△CPHを考えると、三平方の定理が使えて、
$$\small \rm CH^2+HP^2=CP^2$$

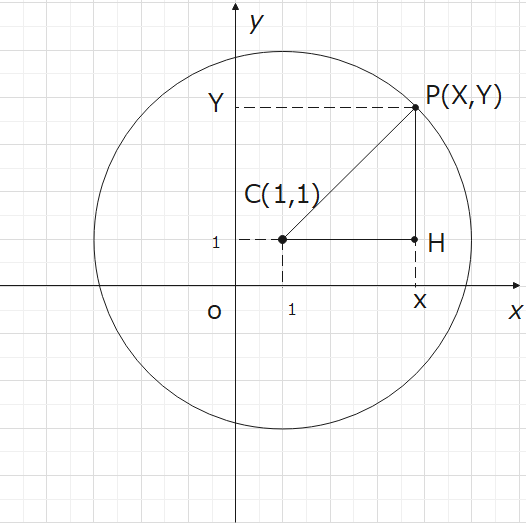
これが、条件式になります。点\(\small P(s,t)\)としてパラメータとしてあらわすならば、 \(\small X = s\)、\(\small Y = t\space\cdots\)①。
また、図から、CH = \(\small |s-1|\)、HP = \(\small |t-1|\)、CP = 2 （点C(1,1)からの距離が2の点をPとしている）なので、条件式に代入して $$\small (s-1)^2+(t-1)^2=4$$ となります。あとは、①から $$\small (X-1)^2+(Y-1)^2=4$$ なので、\(\small X,Y\)を変数化してあげれば(\(\small x,y\)で置き換える)、最初の円の式になります。
\(\small (x-1)^2 + (y-1)^2 = 4\space\cdots\)(答)