文字を含む確率問題の解き方・考え方

管理人のhiroemonです。

本記事では確率に文字が含まれる問題を解説します。確率の応用問題として王道ですが苦手な人も多い分野なので、本記事の解説を読んで苦手を克服していきましょう！

　本記事はこんな人におすすめ

文字が入ると具体的なイメージができなくて考えが止まってしまう…
出てきた答えに自信が持てない…
考え方の道筋を知りたい！

　本記事のレベル

重要度

低

1

2

3

4

5

高
難易度

易しい

1

2

3

4

5

難しい
暗記/理解

暗記重視

1

2

3

4

5

理解重視

文字を含む確率問題に挑戦
まとめ

文字を含む確率問題に挑戦

★本記事で扱う問題

問題[大阪公立大改題]

1回の試行ごとに赤玉か白玉を1個出す機械を考える。この機械からは1回目の試行では赤玉か白玉がそれぞれ$\small \frac{1}{2}$の確率で出るが、2回目以降には直前に出たものと同じ色の玉が$\small \alpha$の確率で、直前に出たものと異なる色の玉が$\small 1-\alpha$の確率で、それぞれ出るものとする。ただし、$\small \alpha$は$\small 0 < \alpha < 1$を満たす定数とする。$\small (n+m)$回目の試行を終えた時点で赤玉が$\small n$個、白玉が$\small m$個出ている確率を$\small P_{n,m}$とする。次の問いに答えよ。
(1)$\small P_{2,2}$を$\small \alpha$の式で表せ。
(2)$\small P_{n,1} (n=1,2,3,\cdots\cdots)$を$\small \alpha$と$\small n$の式で表せ。

★問1の解法と解説

$\small P_{2,2}$の意味

今回の$\small P_{2,2}$の意味は、$\small n=2, m=2$、すなわち問題文から「4回の試行を終えた時点で、赤玉が2個、白玉が2個出ている確率」ということ。

樹形図を用いたパターン整理と各々の確率

確率の問題では、樹形図を描いてパターンを整理するのが鉄則です。

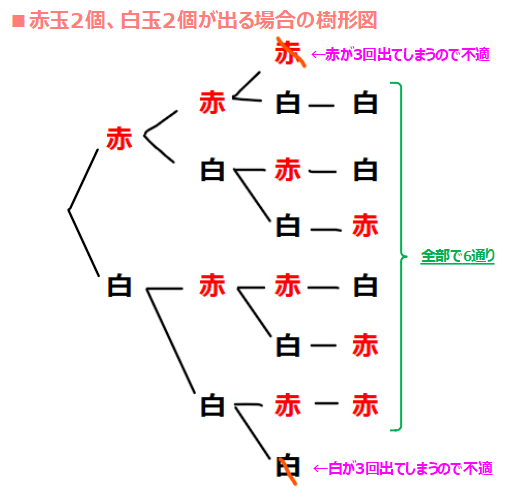
この状況を樹形図にすると以下の通り。

確率計算

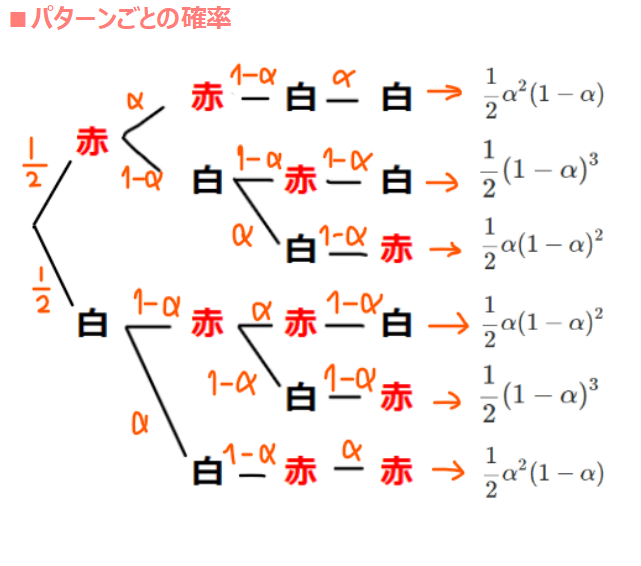
それぞれのパターンごとの確率は、右図の通りなので、各々の確率を足し合わせた確率が今回求める$\small P_{2,2}$となる。

～ひとことアドバイス～
同時に起こらないパターン同士の「確率」や「場合の数」は足し合わせる。
同時に起こるパターン同士の「確率」や「場合の数」はかけ合わせる。

もう少し詳しく知りたい人は「積の法則、和の法則の使い分け（場合の数、確率）」で解説しているのでチェックしてみましょう！

$$
\begin{equation}
\begin{split}
P_{2,2}&=\frac{1}{2}\alpha^2(1-\alpha)\times 2\\
&\quad+\frac{1}{2}(1-\alpha)^3 \times 2\\
&\quad+\frac{1}{2}\alpha(1-\alpha)^2 \times 2\\
&=\alpha^2(1-\alpha)+(1-\alpha)^3+\alpha(1-\alpha)^2\\
&=(1-\alpha)\{\alpha^2+(1-\alpha)^2+\alpha(1-\alpha) \}\\
&=(1-\alpha)\{\alpha^2+(1-\alpha)\{(1-\alpha)+\alpha\}\}\\
&=(1-\alpha)(\alpha^2-\alpha+1)\\
\end{split}
\end{equation}
$$

（(1)の解答）
$$P_{2,2}=(1-\alpha)(\alpha^2-\alpha+1)$$

★問2の解法と解説

■解法のポイント

・小さい数で
・具体的に試しながら
・メカニズムを解き明かすべし！

文字が含まれる確率問題では、問題の状況が抽象的になりやすいので、まずは法則性を理解するために小さい場合で具体的な数字に置き換えて状況を掴むことから始めていきます。

ただし、具体的にするといっても今回の問題の確率$\small \alpha$も具体的にしてしまうと、確率は求まったけど本来、求めたかった文字を含んだ答えを推測するためのメカニズムが解析しにくくなってしまうので注意しましょう。

では解説を始めていきます！

【具体例1】$\small n=1$の場合

$\small P_{n,1}$は、「$\small (n+1)$回目の試行を終えた時点で、赤玉が$\small n$個、白玉が1個出ている確率」です。

まずは、イメージを付けるために、$\small n=1$の場合である$\small P_{1,1}$（=赤玉1個、白玉1個が出る確率）を求めてみます。

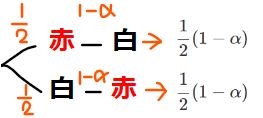
パターンとしては、樹形図からもわかるように、2パターンのみなので、それぞれの確率を足しわせることで

$$
P_{1,1}=\frac{1}{2}(1-\alpha)\times2=(1-\alpha) \quad \cdots①
$$

【具体例2】$\small n=2$の場合

次は、$\small n=2$の場合、すなわち$\small P_{2,1}$（=赤玉2個、白玉1個が出る確率）を求めてみます。

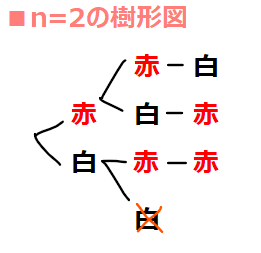
パターンとしては、最初に白玉が出るパターン、2回目に白玉が出るパターン、最後に白玉が出るパターンの全部で3つ。

■最初に白玉が出る確率

「白→赤」の時に1回だけ色が変わるので、
$$\frac{1}{2}\times (1-\alpha)\times \alpha=\frac{1}{2}\alpha(1-\alpha)$$

■2回目に白玉が出る確率

「赤→白」、「白→赤」の時に2回色が変わるので、
$$\frac{1}{2}\times (1-\alpha)\times (1-\alpha)=\frac{1}{2}(1-\alpha)^2$$

■最後に白玉が出る確率

「赤→白」の時に1回だけ色が変わるので、
$$\frac{1}{2}\times \alpha \times (1-\alpha)=\frac{1}{2}\alpha(1-\alpha)$$

よって、計算すると

$$
\begin{equation}
\begin{split}
P_{2,1}&=\frac{1}{2}(1-\alpha)^2+\frac{1}{2}\alpha(1-\alpha)\times2\\
&=\frac{1}{2}\{(1-\alpha)^2+2\alpha(1-\alpha)\}\\
&=\frac{1}{2}(1-2\alpha+\alpha^2+2\alpha-2\alpha^2)\\
&=\frac{1}{2}(1-\alpha^2)\quad \cdots②\\
\end{split}
\end{equation}
$$

規則性の整理と$\small P_{n,1}$の式化

$\small P_{2,1}$の確率を計算する中で、一般的な規則性としてわかるメカニズムが2つあります。皆さんは気づきましたか？それは…

—$\small P_{n,1}$の規則性—
赤玉が$\small n$個、白玉が1個出るパターンは、以下2パターンのいずれかに分けられる。
1. 白玉が最初or最後に出た場合、色が変わるのは1回だけ。
　　
2. 白玉が途中に出た場合(最初or最後以外)、色は2回変わる。
　　

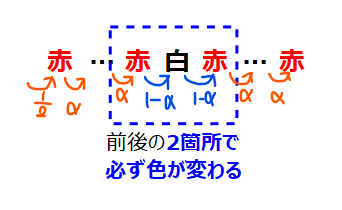
なので、$\small P_{n,1}$を計算したければ、この2つの規則性を数式化して足してあげればokというわけです。

ただし、この規則性は、$\small n=1$の時は規則性の2つ目のパターンがない（赤→白か白→赤のパターンしかないので）ため、以下$\small n \ge 2$の場合に限定して話を進めます（こういう細かい部分は見落としやすいので注意！）。

■規則性1の計算
$\small \alpha$が何回掛け算されているのかわかりにくいですが、そういうときは、小さな数で具体的に考えます。さっき考えた$\small n=2$の場合を見ると、$\small \alpha$は1回だけ掛け算（ここ参照）されています。なので、「$\small n=2$で$\small \alpha$が1回ということは、一般的には$\small \alpha$の掛け算回数は、$\small (n-1)$回になりそうだ」と推測できます。

このことは意外とすぐに証明できて、今回は赤玉が$\small n$個、白玉が1個の計$\small (n+1)$回の試行のうち、初めは必ず$\small \frac{1}{2}$で、色が1回変わる際に$\small (1-\alpha)$の確率を掛け算するので、この2回を差し引いた$\small (n-1)$回が確率$\small \alpha$の積ということになります。

よって、その確率は

$$\frac{1}{2}\alpha^{n-1}(1-\alpha)\times2=\alpha^{n-1}(1-\alpha)\quad \cdots③$$

最後の2倍は、白玉が最初に出る場合と、最後に出る場合の2パターンがあるため。

■規則性2の計算
同様に考えると、今回は、$\small (n+1)$回の試行のうち、初めが$\small \frac{1}{2}$は変わらず、色が変わる確率$\small (1-\alpha)$が2回掛け算されるため、残った$\small (n-2)$回が色が変わらない確率$\small \alpha$の積となる。

よって、その確率は

$$\frac{1}{2}\alpha^{n-2}(1-\alpha)^2\times(n-1)=\frac{1}{2}(n-1)\alpha^{n-2}(1-\alpha)^2\quad \cdots④$$

最後の、$\small (n-1)$倍は、全試行回数$\small (n+1)$回のうち、規則性2に当てはまるようなパターンは、白玉が最初or最後以外に出ればよいので、$\small (n-1)$パターンある。

③、④を足したものが求める確率より、

$$
\begin{equation}
\begin{split}
P_{n,1}&=\alpha^{n-1}(1-\alpha)+\frac{1}{2}(n-1)\alpha^{n-2}(1-\alpha)^2\\
&=\frac{1}{2}\alpha^{n-2}(1-\alpha)\{2\alpha+(n-1)(1-\alpha)\}\\
&=\frac{1}{2}\alpha^{n-2}(1-\alpha)\{(3-n)\alpha+(n-1)\}\\
\end{split}
\end{equation}
$$

ここで、今求めた式は、$\small n \ge 2$の場合だったが、上記の式に$\small n=1$を代入してみると、

$$
\begin{equation}
\begin{split}
P_{1,1}&=\frac{1}{2}\alpha^{1-2}(1-\alpha)\{(3-1)\alpha+(1-1)\}\\
&=\frac{1}{2\alpha}(1-\alpha)\cdot2\cdot\alpha\\
&=(1-\alpha)\\
\end{split}
\end{equation}
$$

なり、①の結果とも合致する。よって、上式は$\small n \ge 1$の場合にも成り立つ。

（(2)の解答）
$$P_{n,1}=\frac{1}{2}\alpha^{n-2}(1-\alpha)\{(3-n)\alpha+(n-1)\}$$

まとめ

文字を含む確率計算問題はいかがでしたか？文字が入ると抽象的でイメージが湧かずに計算が進まない…と悩んでたのが、まずは具体的な小さな数字で実際に計算してみてイメージを膨らませれば、規則性が見えてきて文字が含まれた場合でも計算できそうだ！って思ってもらえていたらこの問題を解いた効果が早速出ている証拠ですね。

他にも確率で文字を含むような計算問題はたくさんあるので、今後随時解説していきたいと思いますので、チェックいただければと思います。

では今回はここまでです。お疲れさまでした！