確率を極めよう(文字を含んだ確率編)

本記事では、文字を含んだ確率の問題の解法について解説します。

　本記事はこんな人におすすめ

文字が入ると具体的なイメージができなくて考えが止まってしまう…
文字を含んだ確率問題の解き方のコツが知りたい！
文字を含んだ確率問題が解きたい！

　本記事で扱う問題

問題[東京大学]

コンピュータの画面に、記号〇と×のいずれかを表示させる操作をくり返し行う。
このとき、各操作で、直前の記号と同じ記号を表示する確率は、それまでの経過に関係なく、$\small p$であるとする。
最初に、コンピュータの画面に×が表示された。操作をくり返し行い、記号×が最初のものも含めて３個出るよりも前に、記号〇が$\small n$個出る確率を$\small P_n$とする。ただし、記号〇が$\small n$個出た段階で操作は終了する。
(1)$\small P_2$を$\small p$で表せ。
(2)$\small n≧3$のとき、$\small P_n$を$\small p$と$\small n$で表せ。

　本記事のレベル

重要度

低

1

2

3

4

5

高
難易度

易しい

1

2

3

4

5

難しい
暗記/理解

暗記重視

1

2

3

4

5

理解重視

【解説編】文字を含んだ確率問題を解くコツ
1. Point①：小さい数で具体的に実験
2. Point②：本質的な計算手順を掴め
【問題・解説編】
1. ★問１の解法と解説
2. ★問２の解法と解説
まとめ

【解説編】文字を含んだ確率問題を解くコツ

問題を解く前に、文字を含んだ確率の問題を解く際のコツを解説します。

～文字を含んだ確率問題を解くコツ～

小さい数で具体的に実験して本質的な計算手順を掴め！

Point①：小さい数で具体的に実験

文字が含まれることで問題が難しく感じるのは、具体的な数字がないことで状況がイメージできないことが原因です。そのため、はじめに問題のイメージを掴むために、具体的な数字で確率を計算をしてみるのが効果的です。計算する際には大きな数字だと計算が複雑になってしまうため、簡単に計算できるような小さい数を設定してあげるのがよいでしょう。

ちなみに、文字が含まれる確率問題の多くは問題の1問目が小さい数字で具体的な確率を求める問題になっていることがほとんどなので、その際に計算してみるでよいですが、Point②でも解説しますが、計算することが目的というよりは、計算の手順を掴むことが目的なので、出題された計算だけでは手順がつかみきれない場合は、必要に応じで別の数字でも計算をしてみるとよいでしょう。

Point②：本質的な計算手順を掴め

具体的な数字で計算することの目的は、確率を求めることではなく、確率を求めるときの計算手順の規則性を把握することです。

文字を含んだ確率問題は、最終的には確率を文字で表すことになります。その際に文字が含まれていても計算できるようにするには、具体的な確率を求める際の計算手順が参考になります。

【問題・解説編】

問題[東京大学]

★問１の解法と解説

$\small P_2$は「×が3個出るよりも前に、〇が2個出る確率」です。実際にどんなパターンがあるか書き出してみるとこんな感じです。

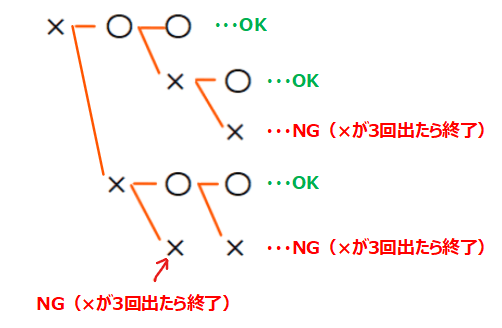
最初が×なので、そこから「〇」「×」と樹形図を描いていき、ルールに従って書き出していくともれなく洗い出すことができます。

そうしたら、次はそれぞれの出現確率を樹形図に書き込んでいきます。直前の記号と同じ記号が出る確率が$\small p$なので、逆に直前の記号とは異なる記号が出る確率は、$\small 1-p$となります。

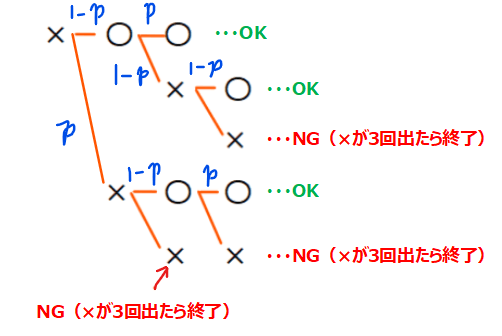
あとは、「OK」となっている3パターンの確率をそれぞれ足し合わせたものが求める確率なので、

$$
\begin{equation}
\begin{split}
P_2&=(1-p)p+(1-p)^3+(1-p)p^2\\
&=(1-p)\{ p+(1-p)^2+p^2\}\\
&=(1-p)(2p^2-p+1)\\
\end{split}
\end{equation}
$$

（解答）
$$P_2=(1-p)(2p^2-p+1)$$

★問２の解法と解説

続いてが本題の一般の$\small n$の場合を求める問題です。求める確率としては、「×が3回出る前に、〇が$\small n$個出る確率」です。

文字を含む場合は、具体的な場合の計算手順を参考にすればよいのでした。問１での計算の流れを改めて振り返ってみましょう。

～問１の計算の流れ～
・樹形図を使ってパターンを洗い出し
・それぞれのパターンごとに確率を書き出し
・全パターンの合計を計算

あとは、これを$\small n$の場合にも当てはめれば。。。って、このままだと$\small n$の場合に樹形図掛けないのでパターンも洗い出せないし確率の計算もできないですよね。。。

ここがまさに文字を含んだ確率を求めるときに大変なところです。今のままだと樹形図も確率も求められないので、問１の解法をもう少しひも解いていきましょう！

パターンに規則性はないか

改めて問１で求めた3パターンを整理したものが以下の図です。

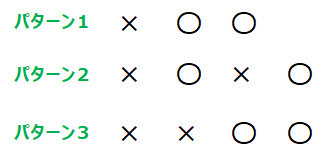
この図を見ると、パターン1が一番シンプルで、初めの×以降はずっと〇が出続けるパターンです。このパターンであれば一般の$\small n$の場合でも、「初めの×以降は〇が$\small n$個連続で出る」パターンなので、簡単にイメージが湧くと思います。

このように、漠然と「複雑そうだな…」とか「いろんなパターンがあって何から手を付けていいかわからない」という場合は、具体的な場合で求めたパターンや計算手順を一つずつ整理して個別に考えてあげると、具体的になりイメージが湧きやすくなります。

では、パターン2や3はどうでしょう。これはなかなかパターンだけ見ていても規則性がつかみづらいかもしれません。

ここで、今回のゲーム（？）のルールを振り返ってみます。

～ゲームのルール～
1.初めは「×」が出ている
2.「〇」が$\small n$個出たら終了
3.「×」が3回出たら終了

こんな感じですね。3つ目は問題文に明記されていませんが、「×」が3回出るよりも前に出た「〇」の個数を数えるというルールから考えると、「×」は3回はでないことが分かります。

では、このルール踏まえて、パターン2、3についてもう少し踏み込んで考えてみます。そうするとるルールから次のようなことが見えてきます。

～ルールからわかる規則性～
1.初めは「×」固定
2.最後は「〇」固定
3.「×」は途中に1回しか出ない

1、2番目はほとんどルール1、2の繰り返しなので大丈夫かなと思います。3つ目の規則について補足しておくと、「×は初めのものを含めて3回出たら終了」ということは、初めの「×」を除けば最後の「〇」が出るまでに罰「×」は多くても1回しか出ないということです。もし仮に「×」が2回出てしまうと、その時点でゲームが終了してしまい「〇」が$\small n$個出なくなります。

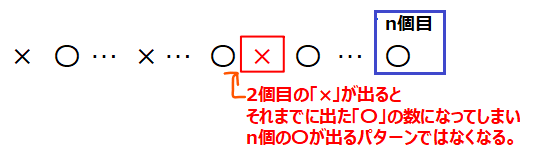
この規則性を踏まえて改めてパターン2、3を見てみましょう。

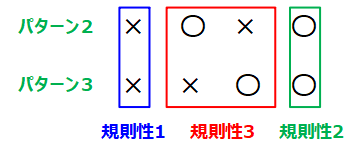
すると、確かに規則性に合致しており、特に赤枠で囲った規則性3のバリエーションによって2つのパターン（「×」がどこに出るか）に分かれていたことまで読み取れるとかなり上級レベルに到達できていると思います。

ここまでくれば、上記の法則を一般の$\small n$の場合にあてはめて図を描くことでパターンの洗い出しができそうです。

パターンの洗い出し

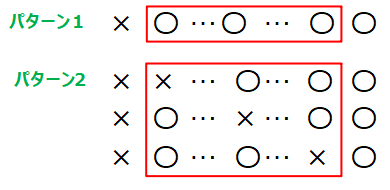
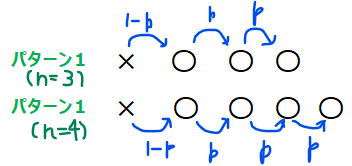
パターン１は初めに「×」が出てからはずっと「〇」が$\small n$個出るパターンです。当たり前ですが、途中の赤枠内もずっと「〇」が続きます。

パターン2は途中に「×」が1回出るパターンです。ではこのパターンは何通りあるでしょうか？こういう時は問１の具体例$\small n=2$の場合からヒントを得ましょう。$\small n=2$の時が2パターンだったので、「一般には$\small n$パターンではないか？」という推測が立てられそうですね。この予想をもとにしっかり計算で確かめていきます。

赤枠で囲った部分は上から順番に「先頭に×が出るパターン」、「途中で×が出るパターン（これがたくさんある）」、「最後に×が出るパターン」というイメージで3つほど書きました。こんな感じで「×」がどこにあるかは赤枠内の×と〇の個数をちゃんと計算してあげれば求まります。頭で計算すると間違えるので、しっかり図で描いて計算するとミスが防げます。

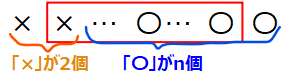
こんな感じで、×が2つと〇が$\small n$個ある（問題的に〇が$\small n$個出たら終了するケースを考えていたので）ので、〇と×の合計は$\small (n+2)$個。そのうち、赤枠内の個数は、先頭の×と最後の〇の計2個を引き算すればよいので$\small n$個と求まります。

よって、パターン2のバリエーションは×が$\small n$箇所のどこにあるかで$\small n$通りです。

確率計算

最後は、求めたパターンごとに確率を計算していきます。

まず、パターン1については、下図のように初めの1回のみ〇の出現確率が$\small 1-p$ですが、それ以降はずっと確率が$\small p$となります。

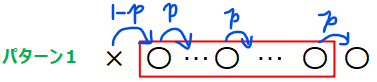
問題はこの$\small p$が何回あるかですが、これも問１からヒントを得て考えていきます。

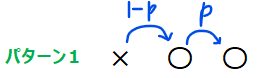
$\small n=2$の時は上図の通り、「〇→〇」への遷移は1回だけです。ということは、一般には$\small (n-1)$回になりそうですね。念のため、裏どり確認しておくと、$\small n=3$の時は2回、$\small n=4$の時は3回になっているので、大丈夫そうです。

よって、パターン1の確率は

$$(1-p)p^{n-1}\quad \cdots ①$$

次にパターン2の確率を求めていきます。先程の通り、「×」が途中のどこで出るかによって$\small n$通りのパターンがありますが、それぞれの確率はどうなるでしょうか？

計算をするうえでポイントになるのは、記号が切り替わるときに確率が変動するので各々のパターンで記号の切り替わりが何回あるかが分かればokです。どのタイミングで記号が変わるかは確率計算には影響しないことに注意しましょう。

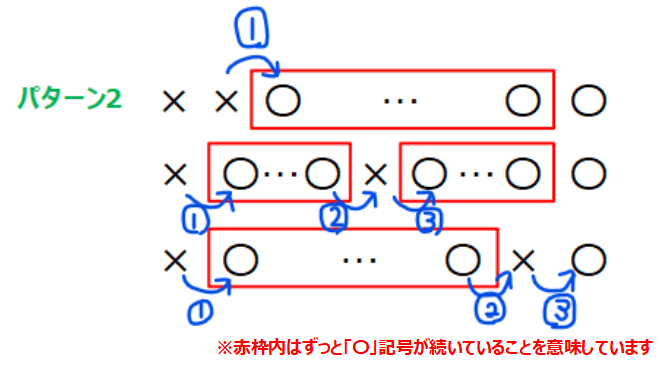
このようにして確認してみると、「「×」が2回目にでる場合のみ、記号の切り替わり回数が2回のみで、それ以外は記号の切り替わり回数は3回」ということが分かります。

ではそれぞれ確率を計算していきます。まずは、「×記号が2回目に出る場合」ですが、「×→×→〇→…→〇」なので、

$$(1-p)p^n \quad \cdots②$$

～補足：$\small p$の指数が$\small n$乗になる理由～
×と〇の記号は合計で$\small (n+2)$回（今考えているパターンから〇が$\small n$回と×が2回）なので、記号から記号への遷移回数は合計で$\small (n+1)$回（「×→×→〇」のように3個記号がある場合、遷移する矢印は2回になるように、遷移回数は記号の個数より1小さくなる）。
よって、全体の遷移回数$\small (n+1)$回のうち、記号が変わる回数が1回（=確率は$\small (1-p)$）なので、残りの$\small n$回が記号が変わらない回数（=確率は$\small p$）。

同様にして、×記号が3つ目以降にある場合は、いずれも記号の切り替わり回数が3回なので、記号が変わらない回数は全体の遷移回数$\small (n+1)$回から3回を引いた$\small (n-2)$回となるので、

$$(1-p)^3p^{n-2}$$

そして、これらの確率は「×」が3回目以降に出た場合で同じになる（記号の切り替わりタイミングは変わるが切り替わりが3回、切り替わらないのが$\small (n-2)$回であることは変わらないので確率を掛け算した結果は同じになる）ので、あとは、パターンの洗い出しで「パターン2」は全体で$\small n$パターンあり、そのうち「×」が2回目に来るパターン以外が今回計算するパターンなので、$\small (n-1)$パターンあることが分かります。

よって、求める確率は先程の確率を$\small (n-1)$倍して

$$(n-1)(1-p)^3p^{n-2}\quad \cdots③$$

長くなりましたが、最後に①～③のパターンを足し合わせたものが求める確率$\small P_n$となるので、

$$
\begin{equation}
\begin{split}
P_n&=(1-p)p^{n-1}+(1-p)p^n+(n-1)(1-p)^3p^{n-2}\\
&=(1-p)p^{n-2}\{p+p^2+(n-1)(1-p)^2\}\\
&=(1-p)p^{n-2}(p+p^2+(n-1)(p^2-2p+1))\\
&=(1-p)p^{n-2}(np^2-(2n-3)p+(n-1))\\
\end{split}
\end{equation}
$$

（解答）
$$P_n=(1-p)p^{n-2}(np^2-(2n-3)p+(n-1))$$