こんにちは。管理人のhiroemonです。
本記事では、極限を求める問題で頻出の「収束条件」、すなわち「極限値を持つための条件」に関する問題を紹介していきたいと思います。
極限はたくさんの分野と組み合わさって出題されることが多いですが、今回は極限と三角関数のコラボ問題になります。それでは、早速始めましょう!
- 収束とか発散とか用語の意味が曖昧…
- 収束条件が覚えられない…
- 問題を解くコツを知りたい
1.用語と公式のおさらい
まずは、今回の問題を解くために理解しておきたい用語と公式について説明します。不安な人は一緒にチェックしましょう!
1.収束、発散とは?
- 発散とは?
→式中の値を無限大にしたときに、式全体の値が\(\small \pm \infty\)になること。- 例:\(\small n^2-n+1\)は、\(\small n\)が無限大のとき、式全体は\(\small \infty\)になるので、発散。
- 収束とは?
→式中の値を無限大にしたときに、式全体の値が1つの値になること。- 例:\(\small \frac{2n+3}{4n-1}\)は、\(\small n\)が無限大のとき、式全体の値は\(\small \frac{1}{2}\)になるので、収束。
発散、収束以外にも値が\(\small \pm 1\)となる振動もあります。
2.収束するための条件
式中のある値を無限大にしたときに、式全体が収束するための条件について、ここでは等比数列の無限項目(\(\small n \to \infty\))で、\(\small r^n\)が収束するのか、発散するのかを解説します。
\(\small r\)を実数とするとき、\(\small n \to \infty\)での\(\small r^n\)の値は以下の通り。
- \(\small r>1\)の時
\(\small r^n\) → \(\small +\infty\)- 掛け算するほど大きくなる。
例:4の無限乗は無限大。
- 掛け算するほど大きくなる。
- \(\small r=1\)の時
\(\small r^n\) → \(\small 1\) ※1の無限乗は1
- \(\small -1<r < 1\)の時
\(\small r^n\) → \(\small 0\)- 分子よりも分母の方が大きいので掛け算するほど0に近づく。
例:\(\small -\frac{1}{3}\)の無限乗は0になる。
- 分子よりも分母の方が大きいので掛け算するほど0に近づく。

- \(\small r=-1\)の時
\(\small r^n\) → \(\small \pm 1\) ※1と-1が交互になる(振動する)
- \(\small r<-1\)の時
\(\small r^n\) → \(\small -\infty\)- 掛け算するほどマイナス方向に大きくなる。
例:-3の無限乗はマイナス無限大になる。
- 掛け算するほどマイナス方向に大きくなる。
入らないです。理由は、\(\small n\)を無限大にしたときに「1つの値にならないから」です。
一見すると+1か-1の値しかとらないので収束しているように思えますが、収束とは極限値が特定の1つの値に定まることなので、\(\small n \to \infty\)で式の値が+1なのか-1なのか定まらない場合は収束していることにはならないので注意しましょう。
2.極限×三角不等式の問題&解説
問題(三角関数を含んだ極限の収束条件)
解法と解説
\(\small r=4\sin^2 \theta+2\cos \theta -3\)とおくと、\(\small a_n=r^n\)が収束する条件を考えればよい。言い換えると、数列\(\small \{a_n\}\)の無限項目(\(\small n \to \infty\))の値が収束する条件を考えればよく、収束条件は\(\small -1 < r \leq 1\)、すなわち、
$$ -1 < 4\sin^2 \theta+2\cos \theta -3 \leq 1$$
である。
ここからは、上記の三角不等式を解く。
1.三角不等式左側の解法
$$
\begin{equation}
\begin{split}
&-1 < 4\sin^2 \theta+2\cos \theta -3\\
&-1 < 4(1-\cos^2 \theta)+2\cos \theta -3\\
&-1 < -4\cos^2 \theta+2\cos \theta +1\\
&4\cos^2 \theta-2\cos \theta -2 < 0\\
&2\cos^2 \theta-\cos \theta -1 < 0\\
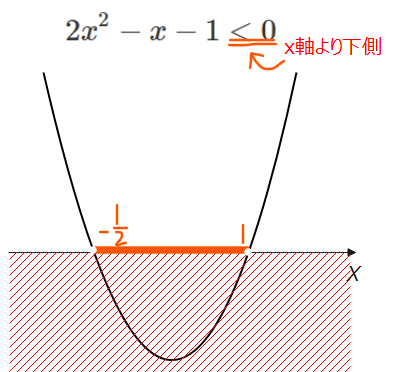
&(2\cos \theta+1)(\cos \theta -1) < 0\\
&-\frac{1}{2}<\cos \theta < 1\\
\end{split}
\end{equation}
$$
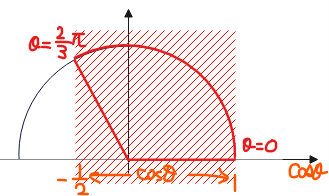
問題の条件である\(\small 0 \leq \theta \leq \pi\)の範囲で上記の三角不等式を解くと、
$$ 0< \theta < \frac{2}{3}\pi \quad \cdots ①$$
※\(\small \cos \theta=x\)とおくと、2次不等式であることが分かりやすい。
2.三角不等式右側の解法
$$
\begin{equation}
\begin{split}
&4\sin^2 \theta+2\cos \theta -3 \leq 1\\
&-4\cos^2 \theta+2\cos \theta +1\leq 1\\
&2\cos^2 \theta-\cos \theta \ge 0\\
&\cos \theta(2\cos \theta-1) \ge 0\\
\end{split}
\end{equation}
$$
よって、
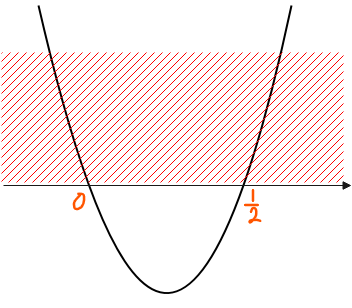
$$\cos \theta \leq 0, \quad \frac{1}{2} \leq \cos \theta$$
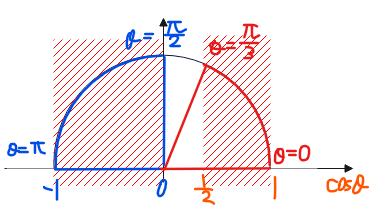
\(\small 0 \leq \theta \leq \pi\)の範囲で上記の三角不等式を解くと、
$$0 \leq \theta \leq \frac{\pi}{3}, \quad \frac{\pi}{2} \leq \theta \leq \pi \quad \cdots ②$$
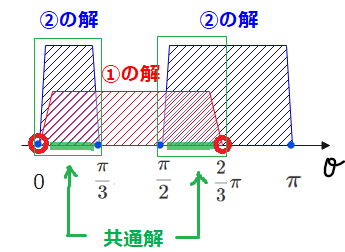
3.共通範囲と解答
①、②の共通範囲が不等式の答えなので、
$$0 < \theta \leq \frac{\pi}{3}, \quad \frac{\pi}{2} \leq \theta < \frac{2}{3}\pi \quad \cdots (答)$$
3.まとめ
今回は、極限の収束条件について解説しました。収束条件が分かっていれば、あとは三角不等式を解くだけだったので、メインは三角不等式の解法の解説になりましたが、いかがでしたか?
冒頭にも述べましたが、極限の問題はいろいろな分野とコラボすることが多いので、他にも「極限×別分野」を解説していこうと思いますので、お楽しみに。一緒に解ける問題を増やしていきましょう!
それでは、今日はここまでです。お疲れさまでした!




