【数学徹底解説】2次不等式の応用（解の条件から不等式を求める）

　本記事のレベル

2次不等式、\(\small x^2+mx-3m>0\)の解がすべての実数となるような定数\(\small m\)の値の範囲を求めよ。

イメージわきにくいですよね。現時点ではざっくりと以下のようなイメージを持てるとよいかと思います。

・2次不等式があって、その中には何やら\(\small m\)という未知の数字がある。
・未知の数字、\(\small m\)の値によって、不等式の左側の2次関数、\(\small y=x^2+mx-3m\)の位置が変わる（x軸と2点で交わるのか、接するのか、または交わらないのか）。

このくらいのイメージができていれば、正直、もう半分くらいは問題を解けたようなものです。上の2点をまとめると、未知数\(\small m\)の値によって、2次関数の位置が変化するんだけど、不等式を解いたとき、答えが「すべての実数」となるような\(\small m\)ってどんな感じ？と聞かれているわけです。解がすべての実数…、どこかで聞いたことがあるフレーズですね？2次不等式の解き方の特殊例として紹介した問題の答えにありましたね。復習がてら、2次不等式の解がすべての実数になるとき、2次関数とx軸との位置関係はどんな絵だったか描けますか？正解は以下のような絵になります。
通常の2次不等式の問題では、不等式から図を描いて、範囲を求めますが、今回は、範囲となる答えから図を描くという逆の作業をする必要があるので、少し難しいと感じたかもしれません。図の書き方は、本投稿の下のほうでトレーニングを用意したので、苦手意識があればそこで猛特訓しましょう！
絵がかけたので、次にそこから読み取れることを考えていきます。x軸と交わらない図を描きました。つまり、2次関数\(\small y=x^2+mx-3m\)は、解をもたないことになりますね。
あとは、判別式を知っている人であれば、解をもたないということは\(\small D=b^2-4ac<0\)なので、
\(\small D=m^2-4×1×(-3m)<0\)
\(\small m^2+12m<0\)
\(\small m(m+12)<0\)
∴\(\small -12<m<0\)
となります。最後は、\(\small m\)についての2次不等式を解く感じです。判別式の詳細は、判別式の使い方を参照してください。

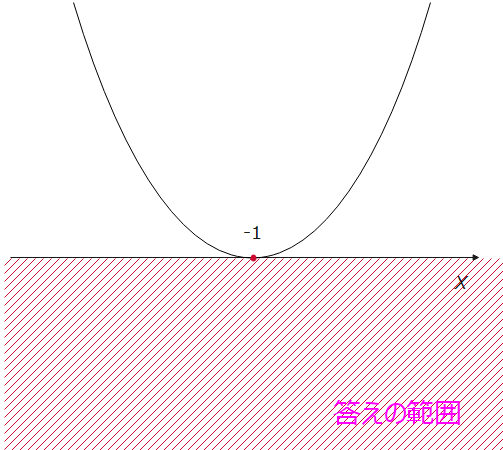
(i)2次不等式、\(\small x^2+mx-3k≦0\)の解が、\(\small x=-1\)となるときの、絵をかけ。
(ii)2次不等式、\(\small -x^2+mx-3k>0\)の解が、\(\small -1<x<3\)となるときの、絵をかけ。
(iii)2次不等式、\(\small x^2+mx-3k>0\)の解が、\(\small x<-1、3<x\)となるときの、絵をかけ。
(iv)2次不等式、\(\small x^2+mx-3k<0\)の解が、すべての実数となるときの、絵をかけ。

(i)絵をかくときは以下の2点に着目します。

　 ★絵を描くときの着眼点
　・\(\small x^2\)の係数：マイナスだったら、両辺に-1をかけて必ずプラスの状態で考える。
　（マイナスだとややこしいので）
　・不等号：答えの範囲が、x軸より上側なのか下側なのか、x軸も含むのかを把握する。

今回は、\(\small x^2\)の係数はプラスなのでそのまま。不等号は0以下なので、答えの範囲はx軸の下側(x軸も含む)。これだけだと、例えば左下のような図を描くことができます。でもこれでは、赤線の答えの範囲に該当する部分がたくさん出てきてしまいますね。今回の問題では、\(\small x=-1\)のみが答えとなるときの絵なので、2次関数の位置は右下の図の位置に決まります（右下の絵が正解）。
(ii)\(\small x^2\)の係数がマイナスなので、全体に-1を掛け算して、係数をプラスにしておきましょう。
\(\small x^2-mx+3k<0\)、こんな感じです。不等号の向きが変わるので注意してください。次に、不等号を見て、x軸より下側(x軸は含まない)です。あとは、答えが、\(\small -1<x<3\)となればいいので、絵としては以下の通り。

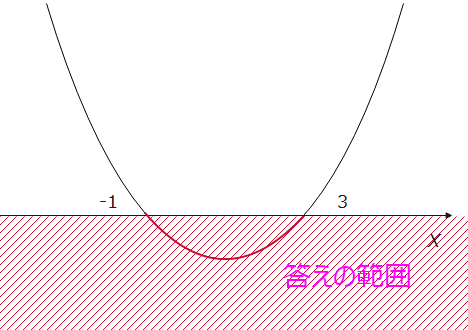
(iii)\(\small x^2\)の係数はプラスなので、そのまま。不等号を見て今回はx軸の上側(x軸は含まない)。\(\small x<-1、3<x\)が答えとなるように絵を描くと以下のようになります。

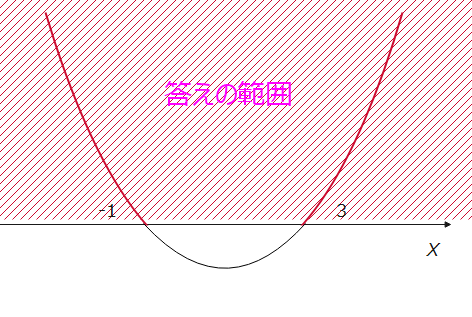
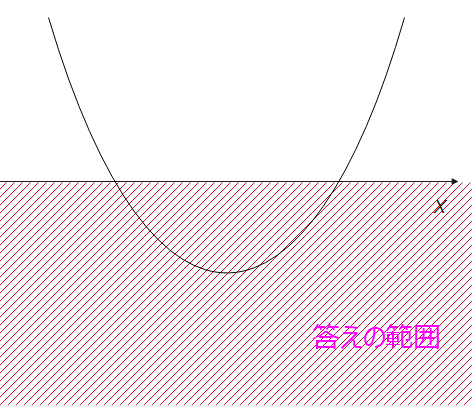
(iv)\(\small x^2\)の係数はプラスなので、そのまま。不等号を見て、答えの範囲はx軸の下側(x軸は含まない)。あとはすべての実数が答えになるように図を描けばよいですね…。今、ん？と思った人はちゃんと理解できているようです。答えがすべての実数になるような絵は描けないというのが正解です。下の図のようにどれだけ頑張っても、2次関数がx軸の上に飛び出てしまうんです。

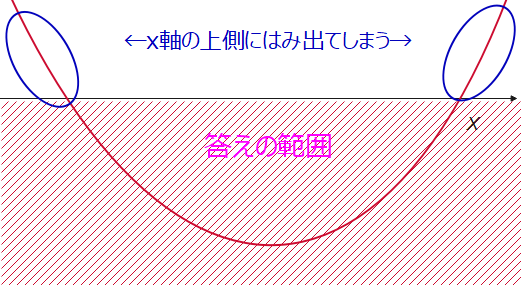
よって、描けないが答えです。

(i)2次不等式、\(\small x^2+mx-3k≦0\)の解が、\(\small x=-1\)となるときの、定数\(\small m、k\)の値を求めよ。

(ii)2次不等式、\(\small -x^2+mx-3k>0\)の解が、\(\small -1<x<3\)となるときの、
　定数\(\small m、k\)の値の範囲を求めよ。

(iii)2次不等式、\(\small x^2+mx-3k>0\)の解が、\(\small x<-1、3<x\)となるときの、
　定数\(\small m、k\)の値の範囲を求めよ。

(iv)2次不等式、\(\small x^2+mx-3k<0\)の解が、すべての実数となるときの、
　定数\(\small m、k\)の値の範囲を求めよ。

(i)トレーニングの絵から、2次関数、\(\small y=x^2+mx-3k\)が\(\small x=-1\)で接するのでこの関数は、\(\small x^2\)の係数が1であることから、 \(\small y=(x+1)^2\) と決まりますね。つまり、もとの2次不等式は、
\(\small (x+1)^2≦0\)
だったとわかります。よって、上の式を展開していくと、
\(\small x^2+2x+1≦0\)
なので、問題文の\(\small y=x^2+mx-3k\)と見比べると、
\(\small m=2\)
\(\small -3k=1\)
とわかります。よって、上の式を解けば、
\(\small m=2\space\cdots\)(答)
\(\small k=-\frac{1}{3}\space\cdots\)(答)

(ii)トレーニングの絵は、途中でマイナスを消した後の2次不等式、\(\small x^2-mx+3k<0\)の絵であることに注意します（後で理由は説明）。絵にかいた2次関数は、\(\small y=(x+1)(x-3)\)とわかります。よって、2次不等式、\(\small x^2-mx+3k<0\)は実は、\(\small (x+1)(x-3)<0\)であったことが分かります。この式を展開すると、
\(\small x^2-2x-3<0\)。
ここで、よし、問題文の2次不等式と見比べて、\(\small m=-2、-3k=-3\)だ！と飛びついてはいけません…。初めに注意した、絵で描いたのは、あくまで\(\small x^2\)の係数のマイナスを消した2次不等式です。確かに\(\small -x^2+mx-3k>0\)と見比べると、\(\small x^2\)の係数にマイナスがないですよね。ほかにも不等号の向きも逆です。もともとは\(\small x^2\)の係数はマイナスだったのを、絵を描くときにややこしくなるからという理由で、全体に-1をかけたんでしたね…。なので、全体を-1倍してもとに戻してあげましょう。
\(\small -x^2+2x+3>0\)
これで不等号の向きも含めて問題文の不等式と全部一致しました。ここでやっと\(\small -x^2+mx-3k>0\)と見比べましょう。
\(\small m=2\)
\(\small -3k=3\)
よって、
\(\small m=2\space\cdots\)(答)
\(\small k=-1\space\cdots\)(答)
(iii)絵にかいた2次関数は(ii)と同じで、\(\small y=(x+1)(x-3)\)です。よって、もとの2次不等式は、\(\small (x+1)(x-3)>0\)。今回は、-1倍などしていないので、そのまま展開して問題文の2次不等式と見比べればOKです。
\(\small (x+1)(x-3)>0\)
\(\small x^2-2x-3>0\)
これが、\(\small x^2+mx-3k>0\)と等しくなるので、
\(\small m=-2\)、 \(\small -3k=-3\)
よって、
\(\small m=-2\space\cdots\)(答)
\(\small k=1\space\cdots\)(答)

(iv)これは、絵が描けなかった問題ですね。当然、「絵が描けない…」なんて解答しても点数がもらえないので、このような場合は、あてはなる答えがないよ、という意味で条件を満たす定数\(\small m、k\)は存在しないなどと答えましょう。

まとめ